Aplicando la ley de Ampère, calculamos el campo magnético producido por una corriente rectilínea de sección circular de radio a. La intensidad de la corriente es i y está uniformemente distribuida en dicha sección.

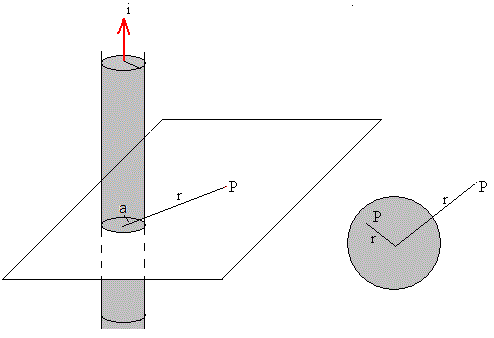
La dirección del campo magnético en el punto P es perpendicular al plano determinado por el eje de la corriente cilíndrica y el punto P, es decir, tangente a la circunferencia de radio r con centro en el eje y que pasa por el punto P.
La simetría de la distribución de corrientes nos indica que el camino cerrado que tenemos que elegir es una circunferencia de radio r, centrada en el eje del cilindro y situada en una plano perpendicular al mismo.

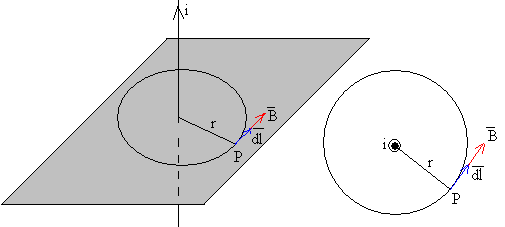
La circulación del campo magnético $\overrightarrow{B}$ a lo largo de dicha circunferencia vale

${\displaystyle {{\displaystyle \oint }}^{\text{}}\overrightarrow{B}·\overrightarrow{dl}={{\displaystyle \oint }}^{\text{}}B·dl·\cos 0=B{{\displaystyle \oint }}^{\text{}}dl=B·2\pi r}$

Como vemos en la figura la dirección del campo magnético $\overrightarrow{B}$ es tangente a la circunferencia, paralela al vector $\overrightarrow{dl}$ , y su módulo es constante en todos los puntos de la circunferencia.

Ley de Ampére

${\displaystyle {{\displaystyle \oint }}^{\text{}}\overrightarrow{B}·\overrightarrow{dl}={\mu }_{0}I}$

I es la intensidad que atraviesa la circunferencia de radio r.

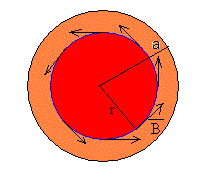	Para r<a Como vemos en la figura, la intensidad que atraviesa la circunferencia de radio r<a es una parte de la intensidad total i. ${\displaystyle B·2\pi r={\mu }_0\left(i\frac{\pi r^2}{\pi R^2}\right)B=\frac{{\mu }_{0}i}{2\pi a^2}r}$
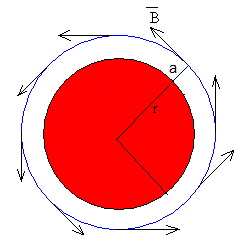	Para r>a La intensidad que atraviesa la circunferencia de radio r>a es i ${\displaystyle B·2\pi r={\mu }_{0}iB=\frac{{\mu }_{0}i}{2\pi r}}$

Representamos el módulo del campo magnético B en función de la distancia radial r

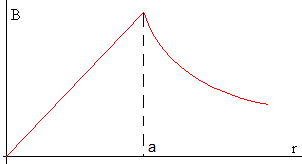
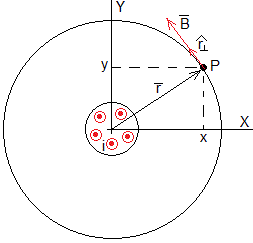
Hemos calculado el módulo B del campo magnético producido por una corriente rectilínea indefinida de radio a en un punto P distante r del eje de la corriente. Su dirección es tangente a la circunferencia de radio r y sentido, la regla de la mano derecha, tal como se muestra en la figura.

El vector unitario $\widehat{r_{\perp }}$ perpendicular a $\overrightarrow{r}$ es

${\displaystyle \begin{array}{l}\overrightarrow{r}=x\widehat{i}+y\widehat{j}\\ \widehat{r_{\perp }}=\frac{-y\widehat{i}+x\widehat{j}}{r}=\frac{-y\widehat{i}+x\widehat{j}}{\sqrt{x^2+y^2}}\end{array}}$

El producto escalar es cero

Expresamos el campo $\overrightarrow{B}$ en el punto P de coordenadas (x,y) de forma vectorial

${\displaystyle \overrightarrow{B}=\{\begin{array}{l}\frac{{\mu }_{0}i}{2\pi }\frac{-y\widehat{i}+x\widehat{j}}{x^2+y^2},r>a\\ \frac{{\mu }_{0}i}{2\pi }\frac{-y\widehat{i}+x\widehat{j}}{a^2},r<a\end{array}}$

Principio de superposición

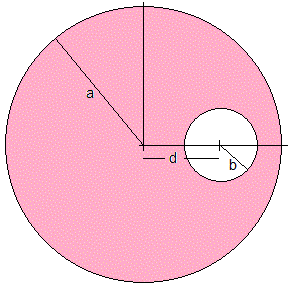
Sea un hilo rectilíneo indefinido de radio a por el que circula una corriente de intensidad i uniformemente distribuida en su sección. El hilo contiene una cavidad de forma cilíndrica de radio b infinitamente larga y paralela al eje de la corriente. La distancia entre los ejes de la corriente y de la cavidad es d tal como se muestra en la figura.

Vamos a utilizar el principio de superposición para calcular el campo magnético en un punto P distante r del eje de la corriente.

El campo magnético producido por la corriente con la cavidad es igual a la diferencia entre el campo magnético producido por una corriente de radio a en el punto P y el campo magnético producido por la cavidad de radio b en dicho punto, ambas corrientes están uniformemente distribuidas en su sección.

Se estudian los tres posibles casos

• El punto P se encuentra dentro de la cavidad, r<a, r'<b
• El punto P se encuentra fuera de la cavidad, pero dentro de la corriente, r<a, r'>b
• El punto P se encuentra fuera de la corriente, r>a

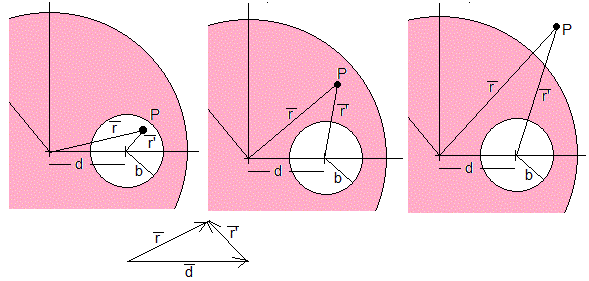
Si la intensidad de la corriente de radio a es i, la intensidad de la corriente que circula por la cavidad es i'

${\displaystyle i\text{'}=\frac{i}{\pi a^2}\pi b^2=i\frac{b^2}{a^2}}$

• El vector campo magnético en el punto P producido por la corriente es

${\displaystyle \overrightarrow{B_1}=\{\begin{array}{l}\frac{{\mu }_{0}i}{2\pi }\frac{-y\widehat{i}+x\widehat{j}}{x^2+y^2},r>a\\ \frac{{\mu }_{0}i}{2\pi }\frac{-y\widehat{i}+x\widehat{j}}{a^2},r<a\end{array}}$

• El vector campo magnético en el punto P producido por la cavidad es

${\displaystyle \begin{array}{l}\overrightarrow{r\text{'}}=\overrightarrow{r}-\overrightarrow{d}=(x-d)\widehat{i}+y\widehat{j}\\ \overrightarrow{B_2}=\{\begin{array}{l}\frac{{\mu }_{0}i\text{'}}{2\pi }\frac{-y\text{'}\widehat{i}+x\text{'}\widehat{j}}{r{\text{'}}^2}=\frac{{\mu }_{0}i}{2\pi }\frac{b^2}{a^2}\frac{-y\widehat{i}+(x-d)\widehat{j}}{{\left(x-d\right)}^2+y^2},r\text{'}>b\\ \frac{{\mu }_{0}i\text{'}}{2\pi }\frac{-y\text{'}\widehat{i}+x\text{'}\widehat{j}}{b^2}=\frac{{\mu }_{0}i}{2\pi a^2}\left(-y\widehat{i}+(x-d)\widehat{j}\right),r\text{'}<b\end{array}\end{array}}$

El campo magnético producido en P por la corriente con cavidad es

• El punto P se encuentra dentro de la cavidad, r<a, r'<b

${\displaystyle \overrightarrow{B}=\overrightarrow{B_1}-\overrightarrow{B_2}=\frac{{\mu }_{0}i}{2\pi }\frac{-y\widehat{i}+x\widehat{j}}{a^2}-\frac{{\mu }_{0}i}{2\pi }\frac{-y\widehat{i}+(x-d)\widehat{j}}{a^2}=\frac{{\mu }_{0}i}{2\pi }\frac{d}{a^2}\widehat{j}}$

• El punto P se encuentra fuera de la cavidad, pero dentro de la corriente, r<a, r'>b

${\displaystyle \begin{array}{l}\overrightarrow{B}=\overrightarrow{B_1}-\overrightarrow{B_2}=\frac{{\mu }_{0}i}{2\pi }\frac{-y\widehat{i}+x\widehat{j}}{a^2}-\frac{{\mu }_{0}i}{2\pi }\frac{b^2}{a^2}\frac{-y\widehat{i}+(x-d)\widehat{j}}{{\left(x-d\right)}^2+y^2}=\\ \frac{{\mu }_{0}i}{2\pi a^2}\left\{y\left(\frac{b^2}{{\left(x-d\right)}^2+y^2}-1\right)\widehat{i}+\left(x-\frac{x-d}{{\left(x-d\right)}^2+y^2}{b}^2\right)\widehat{j}\right\}\end{array}}$

• El punto P se encuentra fuera de la corriente, r>a

${\displaystyle \begin{array}{l}\overrightarrow{B}=\overrightarrow{B_1}-\overrightarrow{B_2}=\frac{{\mu }_{0}i}{2\pi }\frac{-y\widehat{i}+x\widehat{j}}{x^2+y^2}-\frac{{\mu }_{0}i}{2\pi }\frac{b^2}{a^2}\frac{-y\widehat{i}+(x-d)\widehat{j}}{{\left(x-d\right)}^2+y^2}=\\ \frac{{\mu }_{0}i}{2\pi }\left\{y\left(\frac{1}{{\left(x-d\right)}^2+y^2}\frac{b^2}{a^2}-\frac{1}{x^2+y^2}\right)\widehat{i}+\left(\frac{x}{x^2+y^2}-\frac{x-d}{{\left(x-d\right)}^2+y^2}\frac{b^2}{a^2}\right)\widehat{j}\right\}\end{array}}$

Expresamos el campo magnético en términos de magnitudes adimensionales X=x/a, Y=y/a, D=d/a

${\displaystyle \overrightarrow{B}=\{\begin{array}{l}\frac{{\mu }_{0}i}{2\pi a}D\widehat{j},r\text{'}<b\\ \frac{{\mu }_{0}i}{2\pi a}\left\{Y\left(\frac{1}{{\left(X-D\right)}^2+Y^2}\frac{b^2}{a^2}-1\right)\widehat{i}+\left(X-\frac{X-D}{{\left(X-D\right)}^2+Y^2}\frac{b^2}{a^2}\right)\widehat{j}\right\},r\text{'}>b,r<a\\ \frac{{\mu }_{0}i}{2\pi a}\left\{Y\left(\frac{1}{{\left(X-D\right)}^2+Y^2}\frac{b^2}{a^2}-\frac{1}{X^2+Y^2}\right)\widehat{i}+\left(\frac{X}{X^2+Y^2}-\frac{X-D}{{\left(X-D\right)}^2+Y^2}\frac{b^2}{a^2}\right)\widehat{j}\right\},r>a\end{array}}$

Representamos la componente B_y del campo magnético a lo largo del eje X, Y=0, B_x=0 para a=1, b=2/5 y d=1/2

function corriente_hueca
    a=1;
    b=2/5;
    d=1/2;

    f=@(x) cMagnetico(x);
    fplot(f ,[-6,6])
    grid on
    xlabel('x')
    ylabel('B_y')
    title('Campo magnético, en el eje X')

    function z=cMagnetico(x)
        if abs(x)<a
            if x>d-b && x<d+b
                z=d;
            else
                z=x-sign(x-d)*b^2./(abs(x-d)*a^2);
            end
        else
            z=x./x.^2-sign(x-d)*b^2./(abs(x-d)*a^2);
        end
    end
end

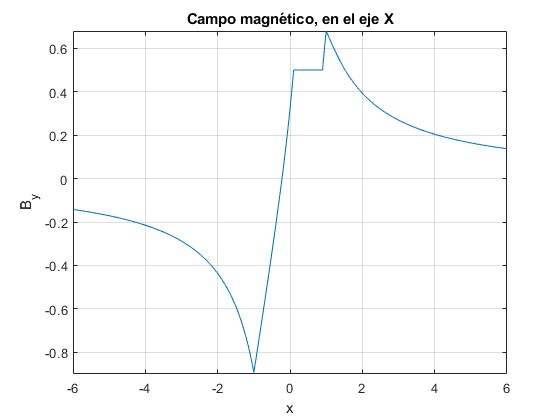
La componente B_y del campo magnético es constante en la cavidad

Representamos mediante flechas el campo magnético en varios puntos del plano XY

function corriente_hueca_1
    a=1;
    b=2/5;
    d=1/2;
    
     hold on
     fplot(@(t) a*cos(t), @(t) a*sin(t),[0,2*pi],'color','k')
     fplot(@(t) d+b*cos(t), @(t) b*sin(t),[0,2*pi],'color','k')
    for x=-2:0.25:2
        for y=-2:0.25:2
            [Bx,By]=cMagnetico(x,y);
            quiver(x, y, Bx, By, 0.5,'color','r')
        end
    end
     hold off
     axis equal
    xlabel('X')
    ylabel('Y')
    title('Campo magnético')

    function [Bx,By]=cMagnetico(x,y)
        if sqrt(x.^2+y.^2)<a
            if sqrt((x-d).^2+y.^2)<b
                Bx=0;
                By=d;
            else
                Bx=y*(b^2./(((x-d).^2+y.^2)*a^2)-1);
                By=x-(x-d)*b^2./(((x-d).^2+y.^2)*a^2);
            end
        else
            Bx=y.*(b^2./(((x-d).^2+y.^2)*a^2)-1./(x.^2+y.^2));
            By=x./(x.^2+y.^2)-(x-d).*b^2/(((x-d).^2+y.^2)*a^2);
        end
    end
end

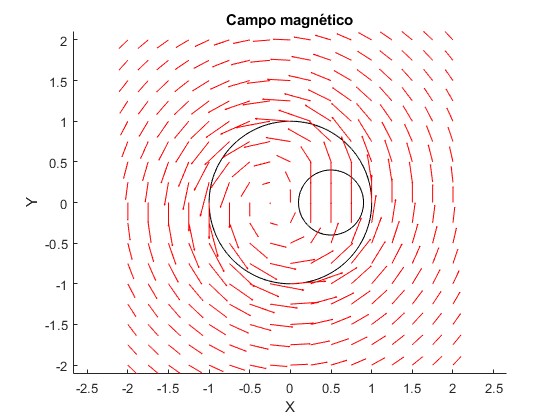
Las circuferencias de color negro, señalan la corriente de radio a y la cavidad de radio b

El efecto de la cavidad se diluye un poco más allá del radio a de la corriente rectilínea e indefinida

Referencias

J. Pierrus. Solved Problems in Classical Electromagnetism. Analytical and numerical solutions with comments. Oxford University Press (2018). Questions 4.12, 4.13, pp. 211-215.