Se produce una fem al girar las espiras en el campo magnético uniforme

${\displaystyle \begin{array}{l}\Phi =\overrightarrow{B}·(N\overrightarrow{S})=BNS\cos \theta \\ V_{\epsilon }=-\frac{d\Phi }{dt}=BNS\sin \theta \frac{d\theta }{dt}\end{array}}$

${\displaystyle iR=V_m-V_{\epsilon }-L\frac{di}{dt}}$

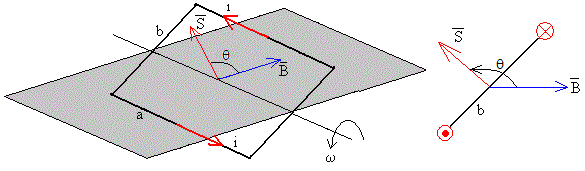
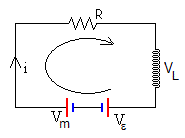
La ecuación del circuito es

${\displaystyle iR=V_0\mathrm{sgn}\left(\sin \theta \right)-BNS\sin \theta \frac{d\theta }{dt}-L\frac{di}{dt}}$

La función sgn (signo de sinθ) describe el conmutador del motor de corriente continua. La fem inducida V_ε se opone, véase la página titulada Autoinducción. Circuito R-L el apartado Ecuación del circuito

Para simplificar las ecuaciones, supondremos que el coeficiente de autoinducción L de las espiras es muy pequeño, por lo que podremos despreciar el término, Ldi/dt

${\displaystyle iR=V_0\mathrm{sgn}\left(\sin \theta \right)-BNS\sin \theta \frac{d\theta }{dt}}$

La ecuación de la dinámica de rotación es

${\displaystyle I\frac{d^2\theta }{d{t}^2}=NiSB\sin \theta -M_{ext}}$

Sustituimos la intensidad i de la ecuación del circuito

${\displaystyle \begin{array}{l}I\frac{d^2\theta }{d{t}^2}=N\frac{V_0\mathrm{sgn}\left(\sin \theta \right)-BNS\sin \theta \frac{d\theta }{dt}}{R}SB\sin \theta -M_{ext}\\ I\frac{d^2\theta }{d{t}^2}=\frac{N{V}_{0}SB}{R}\mathrm{sgn}\left(\sin \theta \right)\sin \theta -\frac{B^2{N}^2{S}^2}{R}{\sin }^2\theta \frac{d\theta }{dt}-M_{ext}\\ I\frac{d^2\theta }{d{t}^2}=\frac{N{V}_{0}SB}{R}\left|\sin \theta \right|-\frac{B^2{N}^2{S}^2}{R}{\sin }^2\theta \frac{d\theta }{dt}-M_{ext}\end{array}}$

Definimos un tiempo τ y dos parámetros β y γ. Para expresar la ecuación diferencial de forma más simple

${\displaystyle \begin{array}{l}\tau =t\sqrt{N\frac{V_0}{I·R}SB},\beta =M_{ext}\frac{R}{N{V}_{0}SB},\gamma =\frac{BNS}{V_0}\sqrt{\frac{NSB{V}_0}{IR}}=\sqrt{\frac{{\left(NSB\right)}^3}{V_{0}IR}}\\ \frac{d^2\theta }{d{\tau }^2}=\left|\sin \theta \right|-\gamma {\sin }^2\theta \frac{d\theta }{d\tau }-\beta \end{array}}$

Resolvemos la ecuación diferencial por el procedimiento ode45 de MATLAB con las siguientes condiciones iniciales, en el instante τ=0, θ=π/2, dθ/dτ=0

• Para γ=0.8 y β=0

El ángulo girado θ crece sin límite

Representamos la velocidad angular de las espiras, dθ/dτ en función del tiempo τ

gamma=0.8;
beta=0;
f=@(t,x) [x(2); abs(sin(x(1)))-gamma*x(2)*sin(x(1))^2-beta]; 
[t,x]=ode45(f,[0,100],[pi/2,0]);
plot(t,x(:,2))
grid on
xlabel('\tau')
ylabel('d\theta/d\tau');
title('Motor de corriente continua')



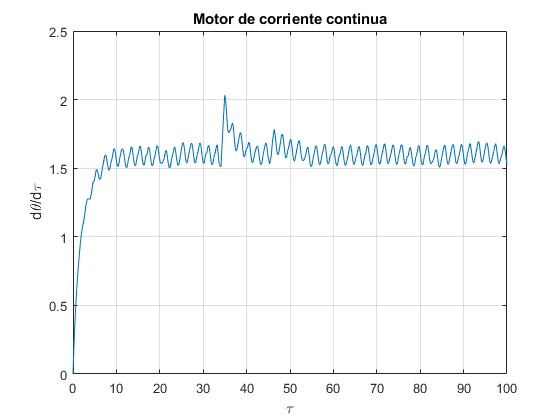
La fem inducida estabiliza la velocidad angular de rotación dθ/dτ. Compárese con la figura al final de la página titulada Fuerza y momento sobre una espira

• Para γ=10 y β=0

Representamos la velocidad angular de las espiras, dθ/dτ en función del tiempo τ



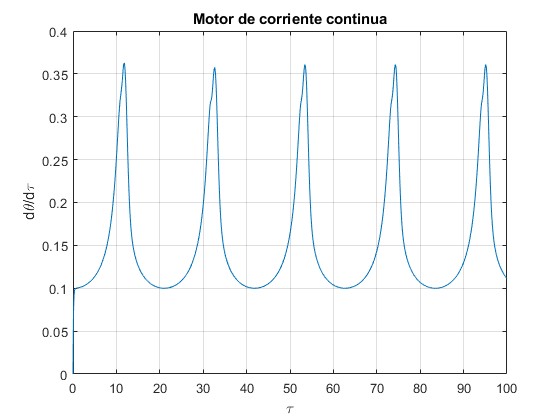
Las fluctuaciones en la velocidad angular dθ/dτ, se incrementan con γ

• Para γ=0.8 y β≠0

Representamos la velocidad angular dθ/dτ en función del tiempo τ para y tres valores del momento externo β=0, 0.1, 0.2

gamma=0.8;
hold on
for beta=[0,0.1,0.2]
    f=@(t,x) [x(2); abs(sin(x(1)))-gamma*x(2)*sin(x(1))^2-beta]; 
    [t,x]=ode45(f,[0,100],[pi/2,0]);
    plot(t,x(:,2))
end
hold off
grid on
xlabel('\tau')
ylabel('d\theta/d\tau');
title('Motor de corriente continua')



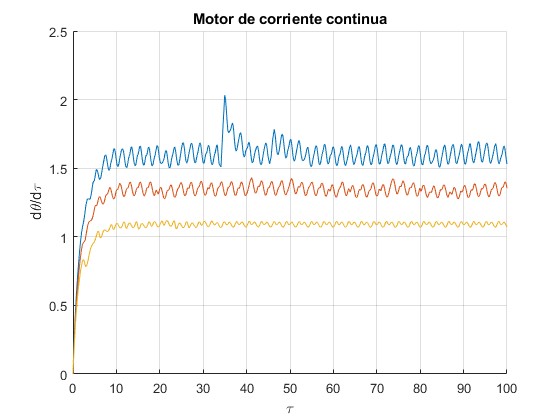
La velocidad angular final disminuye con β. Hay un valor crítico β_c para el cual las espiras oscilan alrededor de una posición de equilibrio tal como se aprecia en las dos figuras más abajo

• Para γ=0.4 y β=0.7

Representamos el ángulo girado por las espiras, θ en función del tiempo τ

gamma=0.4;
beta=0.7;
f=@(t,x) [x(2); abs(sin(x(1)))-gamma*x(2)*sin(x(1))^2-beta]; 
[t,x]=ode45(f,[0,100],[pi/2,0]);
plot(t,x(:,1))
grid on
xlabel('\tau')
ylabel('\theta');
title('Motor de corriente continua')



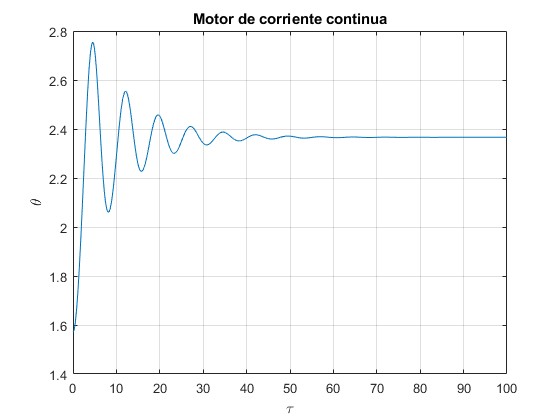
Las espiras oscilan alrededor de la posición de equilibrio estable

Representamos la velocidad angular de las espiras, dθ/dτ en función del tiempo τ

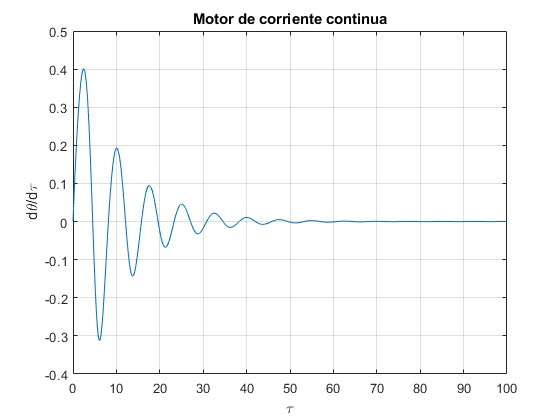
Estado estacionario

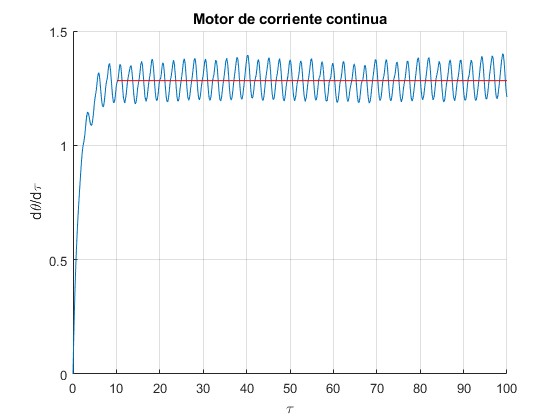
Representamos la velocidad angular dθ/dτ en función del tiempo τ para γ=1.0 y β=0

gamma=1.0;
beta=0;
f=@(t,x) [x(2); abs(sin(x(1)))-gamma*x(2)*sin(x(1))^2-beta]; 
[t,x]=ode45(f,[0,100],[pi/2,0]);
plot(t,x(:,2))
grid on
xlabel('\tau')
ylabel('d\theta/d\tau');
title('Motor de corriente continua')

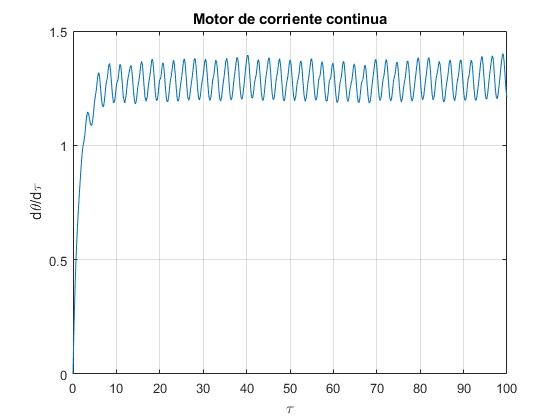
Partimos del hecho de que la velocidad angular media en el estado estacionario ω_T es mucho mayor que la amplitud de las oscilaciones (como se vé en la figura). Esta situación no siempre se produce si γ es grande.

${\displaystyle \left|\frac{d\theta }{dt}-{\omega }_T\right|\ll {\omega }_T}$

Observamos que la velocidad angular oscila alrededor de un valor constante ω_T a partir del tiempo τ≈10. Calculamos el valor medio

${\displaystyle \langle \frac{d\theta }{d\tau }\rangle =\frac{1}{{\tau }_2-{\tau }_1}{\displaystyle \underset{{\tau }_1}{\overset{{\tau }_2}{\int }}\frac{d\theta }{d\tau }d\tau }}$

Obtenemos el valor numérico de la integral, (área bajo la curva) tal como se explica en la página titulada Integración numérica y hallamos el valor medio que denominamos ω_T y lo representamos mediante un segmento de color rojo

gamma=1.0;
 beta=0;
 f=@(t,x) [x(2); abs(sin(x(1)))-gamma*x(2)*sin(x(1))^2-beta]; 
 [t,x]=ode45(f,[0,100],[pi/2,0]);
 plot(t,x(:,2))
 idx=find(t>10); %se toman las velocidades para tiempos mayores que 10
 tt=t(idx);
 v=x(idx,2);
 suma=0; %valor medio
 for k=2:length(tt)
     suma=suma+(tt(k)-tt(k-1))*(v(k-1)+v(k))/2;
 end
 wT=suma/(t(end)-t(idx(1)));
 line([tt(1),tt(end)],[wT,wT],'color','red')
 grid on
 xlabel('\tau')
 ylabel('d\theta/d\tau');
 title('Motor de corriente continua')

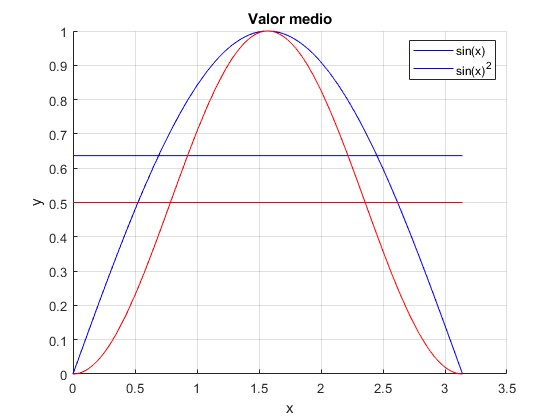
Valor medio de sin(x) y de sin²(x)

${\displaystyle \begin{array}{l}\langle \left|\sin x\right|\rangle =\frac{1}{\pi }{\displaystyle \underset{0}{\overset{\pi }{\int }}\sin x·dx}=\frac{2}{\pi }\\ \langle {\sin }^{2}x\rangle =\frac{1}{\pi }{\displaystyle \underset{0}{\overset{\pi }{\int }}{\sin }^{2}x·dx}=\frac{1}{\pi }{\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{1-\cos \left(2x\right)}{2}·dx=\frac{1}{2}}\end{array}}$

hold on
fplot(@(x) sin(x), [0,pi],'color','b')
line([0,pi],[2/pi,2/pi],'color','b')
fplot(@(x) sin(x).^2, [0,pi],'color','r')
line([0,pi],[1/2,1/2],'color','r')
grid on
xlabel('x')
ylabel('y')
legend('sin(x)','sin(x)^2', 'location', 'best')
title('Valor medio')

Escribimos la ecuación de la dinámica de rotación y tomamos valores medios, como el valor medio de la velocidad angular de rotación ω_T es constante, el valor medio de la aceleración <d²θ/dt²>≈0. Relacionamos el momento externo (carga) M_ext y la velocidad angular media en el estado estacionario ω_T

${\displaystyle \begin{array}{l}I\frac{d^2\theta }{d{t}^2}=\frac{N{V}_{0}SB}{R}\left|\sin \theta \right|-\frac{B^2{N}^2{S}^2}{R}{\sin }^2\theta \frac{d\theta }{dt}-M_{ext}\\ I\langle \frac{d^2\theta }{d{t}^2}\rangle =\frac{N{V}_{0}SB}{R}\langle \left|\sin \theta \right|\rangle -\frac{B^2{N}^2{S}^2}{R}\langle {\sin }^2\theta \frac{d\theta }{dt}\rangle -M_{ext}\\ \frac{N{V}_{0}SB}{R}\frac{2}{\pi }-\frac{B^2{N}^2{S}^2}{R}\frac{1}{2}{\omega }_T-M_{ext}=0\\ {\omega }_T=\frac{4}{\pi }\frac{V_0}{BNS}-\frac{2R}{B^2{N}^2{S}^2}{M}_{ext}\end{array}}$

Cuando el motor no soporta carga alguna, M_ext=0

${\displaystyle {\omega }_{0T}=\frac{4}{\pi }\frac{V_0}{BNS}}$

La velocidad angular media ω_T se hace nula (las espiras oscilan alrededor de una posición de equilibrio estable) para el momento externo M_ext

${\displaystyle \begin{array}{l}0=\frac{4}{\pi }\frac{V_0}{BNS}-\frac{2R}{B^2{N}^2{S}^2}{M}_{ext}\\ M_{ext}=\frac{2}{\pi }\frac{V_{0}BNS}{R}\end{array}}$

En términos del parámetro β

${\displaystyle {\beta }_m=\frac{2}{\pi }\frac{V_{0}BNS}{R}\frac{R}{V_{0}NSB}=\frac{2}{\pi }}$

Desde el estado inicial al estado estacionario

Vamos a estudiar cómo evoluciona la velocidad angular media ω desde el estado incial hasta el estado estacionario caracterizado por una velocidad angular media ω_T. En esta situación, el valor medio de la aceleración angular no es nulo <d²θ/dt²>≠0

${\displaystyle \begin{array}{l}I\frac{d^2\theta }{d{t}^2}=\frac{N{V}_{0}SB}{R}\left|\sin \theta \right|-\frac{B^2{N}^2{S}^2}{R}{\sin }^2\theta \frac{d\theta }{dt}-M_{ext}\\ I\langle \frac{d^2\theta }{d{t}^2}\rangle =\frac{N{V}_{0}SB}{R}\langle \left|\sin \theta \right|\rangle -\frac{B^2{N}^2{S}^2}{R}\langle {\sin }^2\theta \frac{d\theta }{dt}\rangle -M_{ext}\\ \frac{d\omega }{dt}=\frac{N{V}_{0}SB}{IR}\frac{2}{\pi }-\frac{B^2{N}^2{S}^2}{IR}\frac{1}{2}\omega -\frac{M_{ext}}{I}\\ \frac{d\omega }{dt}=\frac{B^2{N}^2{S}^2}{2IR}\left({\omega }_T-\omega \right)\end{array}}$

Integramos, teniendo en cuenta que la velocidad angular inicial es cero

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{\omega }{\int }}\frac{d\omega }{{\omega }_T-\omega }}=\frac{B^2{N}^2{S}^2}{2IR}{\displaystyle \underset{0}{\overset{t}{\int }}dt}\\ -\ln \left({\omega }_T-\omega \right)+\ln {\omega }_T=\frac{B^2{N}^2{S}^2}{2IR}t\\ \frac{{\omega }_T-\omega }{{\omega }_T}=\exp \left(-\frac{t}{t_r}\right),t_r=\frac{2IR}{B^2{N}^2{S}^2}\\ \omega ={\omega }_T\left(1-\exp \left(-\frac{\gamma \tau }{2}\right)\right)\end{array}}$

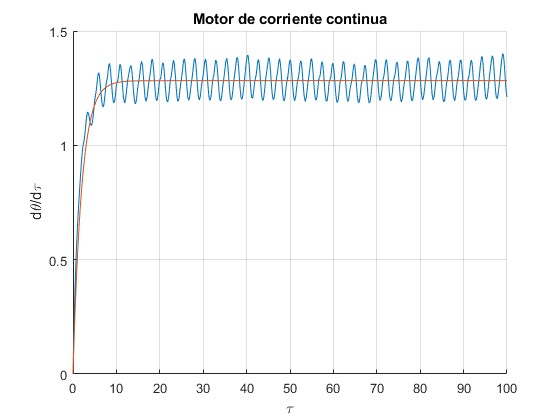
Representamos la velocidad angular dθ/dτ en función del tiempo τ y la funcion ω(τ) que hemos deducido

gamma=1.0;
 beta=0;
 f=@(t,x) [x(2); abs(sin(x(1)))-gamma*x(2)*sin(x(1))^2-beta]; 
 [t,x]=ode45(f,[0,100],[pi/2,0]);
 hold on
 plot(t,x(:,2))
 idx=find(t>10);
 tt=t(idx);
 v=x(idx,2);
 suma=0; %valor medio
 for k=2:length(tt)
     suma=suma+(tt(k)-tt(k-1))*(v(k-1)+v(k))/2;
 end
 wT=suma/(t(end)-t(idx(1)));
 fplot(@(t) wT*(1-exp(-gamma*t/2)),[0,100])
 hold off
 grid on
 xlabel('\tau')
 ylabel('d\theta/d\tau');
 title('Motor de corriente continua')

Energía por unidad de tiempo. Potencia

• Proporcionada por la batería

${\displaystyle \begin{array}{l}{P}_b=V_0\mathrm{sgn}\left(\sin \theta \right)\frac{V_0\mathrm{sgn}\left(\sin \theta \right)-BNS\sin \theta \frac{d\theta }{dt}}{R}=\frac{V_0^2}{R}-\frac{V_0}{R}BNS\left|\sin \theta \right|\frac{d\theta }{dt}\\ =\frac{V_0^2}{R}\left(1-\frac{BNS}{V_0}\left|\sin \theta \right|\frac{d\theta }{dt}\right)=\frac{V_0^2}{R}\left(1-\frac{BNS}{V_0}\sqrt{\frac{N{V}_{0}BS}{IR}}\left|\sin \theta \right|\frac{d\theta }{d\tau }\right)\\ P_b=\frac{V_0^2}{R}\left(1-\gamma \left|\sin \theta \right|\frac{d\theta }{d\tau }\right)\end{array}}$

• Disipada en la resistencia

${\displaystyle \begin{array}{l}{P}_d={\left(\frac{V_0\mathrm{sgn}\left(\sin \theta \right)-BNS\sin \theta \frac{d\theta }{dt}}{R}\right)}^{2}R=\frac{1}{R}\left(V_0^2+B^2{N}^2{S}^2{\sin }^2\theta {\left(\frac{d\theta }{dt}\right)}^2-2V_{0}BNS\left|\sin \theta \right|\frac{d\theta }{dt}\right)=\\ \frac{V_0^2}{R}\left(1+{\left(\frac{BNS}{V_0}\right)}^2{\sin }^2\theta {\left(\frac{d\theta }{dt}\right)}^2-2\frac{BNS}{V_0}\left|\sin \theta \right|\frac{d\theta }{dt}\right)\\ P_d=\frac{V_0^2}{R}{\left(1-\gamma \left|\sin \theta \right|\frac{d\theta }{d\tau }\right)}^2\end{array}}$

• Suministrada a los dispositivos externos (carga)

${\displaystyle \begin{array}{l}{P}_e=M_{ext}\frac{d\theta }{dt}=\frac{N{V}_{0}SB}{R}\beta \frac{d\theta }{d\tau }\sqrt{\frac{N{V}_{0}SB}{IR}}=\frac{V_0^2}{R}\left(\frac{NSB}{V_0}\sqrt{\frac{NSB{V}_0}{IR}}\right)\beta \frac{d\theta }{d\tau }\\ P_e=\frac{V_0^2}{R}\gamma \beta \frac{d\theta }{d\tau }\end{array}}$

• Cambio de energía cinética de rotación de las espiras, con el tiempo

${\displaystyle \begin{array}{l}\frac{d{E}_k}{dt}=\frac{d}{dt}\left(\frac{1}{2}I{\omega }^2\right)=I\omega \frac{d\omega }{dt}=\left(\frac{d\theta }{dt}\right)\left(\frac{N{V}_{0}SB}{R}\left|\sin \theta \right|-\frac{B^2{N}^2{S}^2}{R}{\sin }^2\theta \frac{d\theta }{dt}-M_{ext}\right)=\\ \frac{N{V}_{0}SB}{R}\left|\sin \theta \right|\frac{d\theta }{dt}-\frac{B^2{N}^2{S}^2}{R}{\sin }^2\theta {\left(\frac{d\theta }{dt}\right)}^2-M_{ext}\frac{d\theta }{dt}=\\ \frac{N{V}_{0}SB}{R}\left|\sin \theta \right|\frac{d\theta }{d\tau }\sqrt{\frac{N{V}_{0}SB}{IR}}-\frac{B^2{N}^2{S}^2}{R}{\sin }^2\theta {\left(\frac{d\theta }{d\tau }\right)}^2\frac{N{V}_{0}SB}{IR}-\frac{V_0^2}{R}\gamma \beta \frac{d\theta }{d\tau }\\ \frac{V_0^2}{R}\left(\frac{NSB}{V_0}\sqrt{\frac{N{V}_{0}SB}{IR}}\right)\left|\sin \theta \right|\frac{d\theta }{d\tau }-\frac{V_0^2}{R}\frac{B^3{N}^3{S}^3}{V_{0}IR}{\sin }^2\theta {\left(\frac{d\theta }{d\tau }\right)}^2-\frac{V_0^2}{R}\gamma \beta \frac{d\theta }{d\tau }=\\ \frac{V_0^2}{R}\left(\gamma \left|\sin \theta \right|\frac{d\theta }{d\tau }-{\gamma }^2{\sin }^2\theta {\left(\frac{d\theta }{d\tau }\right)}^2-\gamma \beta \frac{d\theta }{d\tau }\right)\end{array}}$

Conservación de la energía, comprobamos que

${\displaystyle \begin{array}{l}{P}_b=P_d+P_e+\frac{d{E}_k}{dt}\\ \frac{V_0^2}{R}\left(1-\gamma \left|\sin \theta \right|\frac{d\theta }{d\tau }\right)=\frac{V_0^2}{R}{\left(1-\gamma \left|\sin \theta \right|\frac{d\theta }{d\tau }\right)}^2+\frac{V_0^2}{R}\gamma \beta \frac{d\theta }{d\tau }+\frac{V_0^2}{R}\left(\gamma \left|\sin \theta \right|\frac{d\theta }{d\tau }-{\gamma }^2{\sin }^2\theta {\left(\frac{d\theta }{d\tau }\right)}^2-\gamma \beta \frac{d\theta }{d\tau }\right)\end{array}}$

Valores medios

• Suministrada por la batería

${\displaystyle \begin{array}{l}{P}_b=\frac{V_0^2}{R}\left(1-\frac{BNS}{V_0}\left|\sin \theta \right|\frac{d\theta }{dt}\right)\\ \langle P_b\rangle =\frac{V_0^2}{R}\left(1-\frac{BNS}{V_0}\langle \left|\sin \theta \right|\frac{d\theta }{dt}\rangle \right)\\ \langle P_b\rangle =\frac{V_0^2}{R}\left(1-\frac{BNS}{V_0}\langle \left|\sin \theta \right|\rangle \langle \frac{d\theta }{dt}\rangle \right)\\ \langle P_b\rangle =\frac{V_0^2}{R}\left(1-\frac{BNS}{V_0}\frac{2}{\pi }{\omega }_T\right)=\frac{V_0^2}{R}\left(1-\frac{BNS}{V_0}\frac{2}{\pi }\left(\frac{4}{\pi }\frac{V_0}{BNS}-\frac{2R}{B^2{N}^2{S}^2}{M}_{ext}\right)\right)\\ \langle P_b\rangle =\frac{V_0^2}{R}\left(1-\frac{8}{{\pi }^2}\right)+\frac{4V_0}{\pi BNS}{M}_{ext}\end{array}}$

En términos del parámetro β

${\displaystyle \langle P_b\rangle =\frac{V_0^2}{R}\left(1-\frac{8}{{\pi }^2}\right)+\frac{4V_0}{\pi BNS}\frac{V_{0}NSB}{R}\beta =\frac{V_0^2}{R}\left(1-\frac{8}{{\pi }^2}+\frac{4}{\pi }\beta \right)}$

En ausencia de carga M_ext=0, la potencia media suministrada por la batería es independiente de los detalles del motor (espiras y campo magnético)

${\displaystyle \langle P_b\rangle =\frac{V_0^2}{R}\left(1-\frac{8}{{\pi }^2}\right)=0.189\frac{V_0^2}{R}}$

• Disipada en la resistencia

${\displaystyle \begin{array}{l}{P}_d=\frac{V_0^2}{R}\left(1+{\left(\frac{BNS}{V_0}\right)}^2{\sin }^2\theta {\left(\frac{d\theta }{dt}\right)}^2-2\frac{BNS}{V_0}\left|\sin \theta \right|\frac{d\theta }{dt}\right)\\ \langle P_d\rangle =\frac{V_0^2}{R}\left(1+{\left(\frac{BNS}{V_0}\right)}^2\langle {\sin }^2\theta \rangle \langle {\left(\frac{d\theta }{dt}\right)}^2\rangle -2\frac{BNS}{V_0}\langle \left|\sin \theta \right|\rangle \langle \frac{d\theta }{dt}\rangle \right)\\ \langle P_d\rangle =\frac{V_0^2}{R}\left(1+{\left(\frac{BNS}{V_0}\right)}^2\frac{1}{2}{\omega }_T^2-2\frac{BNS}{V_0}\frac{2}{\pi }{\omega }_T\right)=\\ \frac{V_0^2}{R}\left(1+{\left(\frac{BNS}{V_0}\right)}^2\frac{1}{2}{\left(\frac{4}{\pi }\frac{V_0}{BNS}-\frac{2R}{B^2{N}^2{S}^2}{M}_{ext}\right)}^2-2\frac{BNS}{V_0}\frac{2}{\pi }\left(\frac{4}{\pi }\frac{V_0}{BNS}-\frac{2R}{B^2{N}^2{S}^2}{M}_{ext}\right)\right)=\\ \frac{V_0^2}{R}\left(1-\frac{8}{{\pi }^2}+\frac{2R^2}{B^2{N}^2{S}^2{V}_0^2}{M}_{ext}^2\right)=\frac{V_0^2}{R}\left(1-\frac{8}{{\pi }^2}\right)+\frac{2R}{B^2{N}^2{S}^2}{M}_{ext}^2\end{array}}$

• Suministrada a los dispositivos externos (carga)

${\displaystyle \begin{array}{l}\langle P_e\rangle =M_{ext}\langle \frac{d\theta }{dt}\rangle =M_{ext}{\omega }_T=M_{ext}\left(\frac{4}{\pi }\frac{V_0}{BNS}-\frac{2R}{B^2{N}^2{S}^2}{M}_{ext}\right)\\ \frac{4}{\pi }\frac{V_0}{BNS}{M}_{ext}-\frac{2R}{B^2{N}^2{S}^2}{M}_{ext}^2\end{array}}$

En términos del parámetro β

${\displaystyle \langle P_e\rangle =\frac{4}{\pi }\frac{V_0}{BNS}\frac{N{V}_{0}SB}{R}\beta -\frac{2R}{B^2{N}^2{S}^2}{\left(\frac{N{V}_{0}SB}{R}\beta \right)}^2=\frac{V_0^2}{R}\left(\frac{4}{\pi }\beta -2{\beta }^2\right)}$

• Cambio de energía cinética de rotación de las espiras con el tiempo

En el estado estacionario

${\displaystyle \langle \frac{d{E}_k}{dt}\rangle =0}$

Comprobación

${\displaystyle \begin{array}{l}\langle P_b\rangle =\langle P_d\rangle +\langle P_e\rangle \\ \frac{V_0^2}{R}\left(1-\frac{8}{{\pi }^2}\right)+\frac{4V_0}{\pi BNS}{M}_{ext}=\frac{V_0^2}{R}\left(1-\frac{8}{{\pi }^2}\right)+\frac{2R}{B^2{N}^2{S}^2}{M}_{ext}^2+\frac{4}{\pi }\frac{V_0}{BNS}{M}_{ext}-\frac{2R}{B^2{N}^2{S}^2}{M}_{ext}^2\end{array}}$

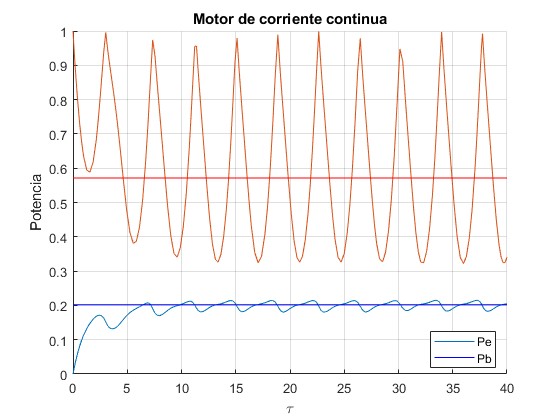
Representamos la potencia suministrada por la batería P_b y la proporcionada a los dispositivos externos P_e, para γ=0.8 y β=0.3. Las líneas horizontales representan los valores medios

gamma=0.8;
beta=0.3;
%V^2/R=1
f=@(t,x) [x(2); abs(sin(x(1)))-gamma*x(2)*sin(x(1))^2-beta]; 
[t,x]=ode45(f,[0,40],[pi/2,0]);
hold on
Pe=beta*gamma*x(:,2); %externa
plot(t,Pe)
Pe_media=4*beta/pi-2*beta^2;
line([0,40],[Pe_media,Pe_media],'color','b')
Pb=1-gamma*abs(sin(x(:,1))).*x(:,2);
plot(t,Pb)
Pb_media=1-8/pi^2+4*beta/pi;
line([0,40],[Pb_media,Pb_media],'color','r')
disp(Pe_media/Pb_media)
hold off
grid on
xlabel('\tau')
legend('Pe','Pb','location','best')
ylabel('Potencia');
title('Motor de corriente continua')

El rendimiento del motor de corriente continua es el cociente entre la potencia media suministrada a los dispositivos externos <P_e> y la suministrada por la batería <P_b>

 0.3535

${\displaystyle \eta =\frac{\langle P_e\rangle }{\langle P_b\rangle }=\frac{\frac{4}{\pi }\beta -2{\beta }^2}{1-\frac{8}{{\pi }^2}+\frac{4}{\pi }\beta }}$

Representamos el rendimiento η en función de β en el intervalo 0≤β≤β_m, es decir, 0≤β≤2/π

f=@(x) (4*x/pi-2*x.^2)./(1-8/pi^2+4*x/pi);
hold on
fplot(f,[0,2/pi])
x1=2/pi-(pi-sqrt(pi^2-8))/4;
max=(pi-sqrt(pi^2-8))^2/8;
line([x1,x1],[0,max],'lineStyle','--')
hold off
disp([x1,f(x1)])
grid on
ylim([0,0.4])
xlabel('\beta')
ylabel('\eta')
title('Rendimiento')

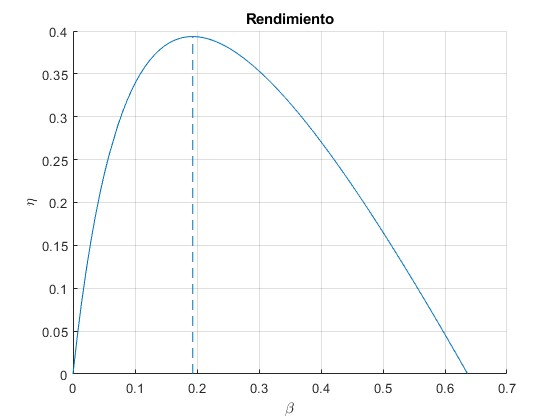
   0.1931    0.3935

Presenta un máximo para β=0.19 y su valor es η=0.39

${\displaystyle \begin{array}{l}\frac{d\eta }{d\beta }=0\\ \left(\frac{4}{\pi }-4\beta \right)\left(1-\frac{8}{{\pi }^2}+\frac{4}{\pi }\beta \right)-\left(\frac{4}{\pi }\beta -2{\beta }^2\right)\frac{4}{\pi }=0\\ \frac{8}{{\pi }^2}{\beta }^2+\left(4-\frac{32}{{\pi }^2}\right)\beta +\frac{32}{{\pi }^3}-\frac{4}{\pi }=0\\ {\beta }_1=\frac{2}{\pi }-\frac{1}{4}\left(\pi -\sqrt{{\pi }^2-8}\right)\\ {\eta }_{máx}=\frac{\frac{4}{\pi }-2{\beta }_1}{1-\frac{8}{{\pi }^2}+\frac{4}{\pi }{\beta }_1}{\beta }_1=\frac{\frac{4}{\pi }-2\left(\frac{2}{\pi }-\frac{1}{4}\left(\pi -\sqrt{{\pi }^2-8}\right)\right)}{1-\frac{8}{{\pi }^2}+\frac{4}{\pi }\left(\frac{2}{\pi }-\frac{1}{4}\left(\pi -\sqrt{{\pi }^2-8}\right)\right)}\left(\frac{2}{\pi }-\frac{1}{4}\left(\pi -\sqrt{{\pi }^2-8}\right)\right)=\\ \frac{\pi }{2}\frac{\left(\pi -\sqrt{{\pi }^2-8}\right)}{\sqrt{{\pi }^2-8}}\left(\frac{\sqrt{{\pi }^2-8}}{4}-\frac{{\pi }^2-8}{4\pi }\right)=\frac{1}{8}{\left(\pi -\sqrt{{\pi }^2-8}\right)}^2\end{array}}$

Referencias

Enrique F Moreno. Numerical investigation of the DC electric motor. Eur. J. Phys. 39 (2018) 055203