Lemniscata de Bernoulli

La ecuación de la Lemniscata de Bernouilli en coordenadas polares es

r²=a²cos(2θ), -π/4≤θ≤π/4

a=1;
th=linspace(-pi/4,pi/4,200);
r=a*sqrt(cos(2*th));
x=r.*cos(th);
y=r.*sin(th);
hold on
plot(x,y, 'b')
plot(-x,y,'b')
hold off
axis equal
grid on
xlabel('x')
ylabel('y')
title('Lemniscata de Bernoulli')

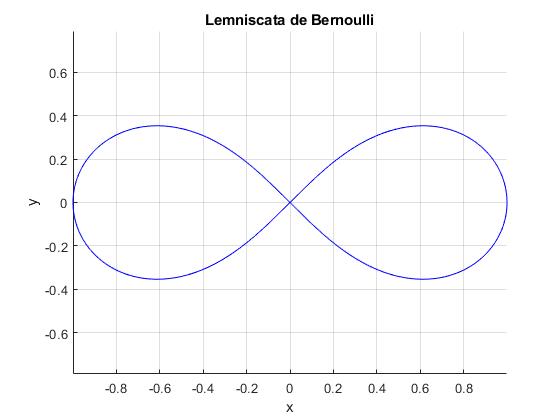
La longitud de la lemniscata de Bernoulli es:

${\displaystyle l=4{\displaystyle \underset{0}{\overset{\pi /4}{\int }}ds}}$

Calculamos la longitud de arco ds de una porción infinitesimal de la lemniscata de Bernoulli

${\displaystyle \begin{array}{l}\{\begin{array}{l}x=r\cos \theta \\ y=r\sin \theta \end{array}\\ \{\begin{array}{l}dx=\cos \theta ·dr-r\sin \theta ·d\theta \\ dy=\sin \theta ·dr+r\cos \theta ·d\theta \end{array}\\ d{s}^2=d{x}^2+d{y}^2=d{r}^2+r^{2}d{\theta }^2\\ r^2=a^2\cos (2\theta )\\ rdr=-a^2\sin (2\theta )·d\theta \\ d{s}^2=a^2\frac{d{\theta }^2}{\cos (2\theta )}\end{array}}$

Integramos, respecto del ángulo, θ

${\displaystyle l=4{\displaystyle \underset{0}{\overset{\pi /4}{\int }}ds}=4a{\displaystyle \underset{0}{\overset{\pi /4}{\int }}\frac{d\theta }{\sqrt{\cos (2\theta )}}}}$

Hacemos el cambio de variable

${\displaystyle \{\begin{array}{l}\cos (2\theta )={\cos }^2\phi \\ -2\sin (2\theta )·d\theta =-2\cos \phi \sin \phi ·d\phi \end{array}}$

La integral se convierte en

${\displaystyle \begin{array}{l}l=4a{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\frac{\sin \phi d\phi }{\sqrt{1-{\cos }^4\phi }}}=4a{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\frac{d\phi }{\sqrt{1+{\cos }^2\phi }}=4a{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\frac{d\phi }{\sqrt{2-{\sin }^2\phi }}}}=\\ \frac{4a}{\sqrt{2}}{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\frac{d\phi }{\sqrt{1-\frac{1}{\sqrt{2}}{\sin }^2\phi }}}=\frac{4a}{\sqrt{2}}K\left(\frac{1}{\sqrt{2}}\right)\end{array}}$

>> 4*ellipke(1/2)/sqrt(2)
ans =    5.2441

La integral elíptica completa de primera especie es

${\displaystyle K(k)={\displaystyle \underset{0}{\overset{\pi /2}{\int }}\frac{d\phi }{\sqrt{1-k^2{\sin }^2\phi }}}}$

Una integral similar, la encontramos al calcular el periodo de un péndulo para cualquier amplitud θ₀<π

Una generalización de esta integral

${\displaystyle F(\theta ,k)={\displaystyle \underset{0}{\overset{\theta }{\int }}\frac{d\phi }{\sqrt{1-k^2{\sin }^2\phi }}}0\le \theta \le \frac{\pi }{2}}$

se denomina integral elíptica incompleta de primera especie.

En la página titulada 'Caída del extremo libre de una cadena doblada' se utilizan las integrales elípticas imcompletas

Longitud de una elipse

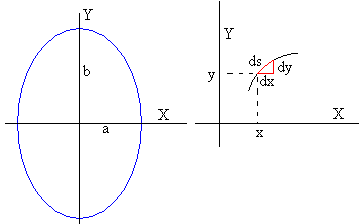
La ecuación de una elipse de semiejes a y b es

${\displaystyle \frac{x^2}{a^2}+\frac{y^2}{b^2}=1}$

o en forma paramétrica
x=a·cosφ
y=b·sinφ

Como podemos ver a la derecha de la figura, la longitud de un elemento diferencial ds del arco de la elipse es

${\displaystyle \begin{array}{l}ds=\sqrt{d{x}^2+d{y}^2}=\sqrt{a^2{\sin }^2\phi +b^2{\cos }^2\phi }·d\phi =b\sqrt{1-\frac{b^2-a^2}{b^2}{\sin }^2\phi }·d\phi \\ =b\sqrt{1-k^2{\sin }^2\phi }·d\phi (b>a)\end{array}}$

La longitud de la elipse es

${\displaystyle L=b{\displaystyle \underset{0}{\overset{2\pi }{\int }}\sqrt{1-k^2{\sin }^2\phi }·d\phi =4}b{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\sqrt{1-k^2{\sin }^2\phi }·d\phi }}$

Habitualmente, el semieje mayor, a>b

${\displaystyle L=4a{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\sqrt{1-k^2{\sin }^2\phi }}d\phi ,k^2=\frac{a^2-b^2}{a^2}={\epsilon }^2,a>b}$

donde ε es la excentricidad de la elipse

La integral elíptica completa de segunda especie es

${\displaystyle E(k)={\displaystyle \underset{0}{\overset{\pi /2}{\int }}\sqrt{1-k^2{\sin }^2\phi }·d\phi }}$

Una expresión aproximada debida a Ramanujan es

${\displaystyle L\approx \pi \left(3(a+b)-\sqrt{(3a+b)(a+3b)}\right)}$

Calculamos la longitud del arco de una elipse de semiejes a=2 y b=1.

>> a=2; b=1;
>> e=sqrt(a^2-b^2)/a;
>> [K,E]=ellipke(e^2);
>> 4*a*E
ans =    9.6884
>> pi*(3*(a+b)-sqrt((3*a+b)*(a+3*b)))
ans =    9.6884

Una generalización de esta integral es

${\displaystyle E(\theta ,k)={\displaystyle \underset{0}{\overset{\theta }{\int }}\sqrt{1-k^2{\sin }^2\phi }·d\phi }}$

se denomina integral elíptica incompleta de segunda especie.

En la páginas tituladas 'Caída de una varilla inclinada', 'Caída del extremo libre de una cadena doblada' y 'Oscilaciones del líquido contenido en dos vasos comunicantes' se utilizan integrales elípticas completas e incompletas

Periodicidad

Las funciones elípticas E(θ,k) y F(θ,k) tiene una periodicidad que se expresa de la siguiente forma

${\displaystyle \begin{array}{l}E(\theta +n\pi ,k)=E(\theta ,k)+2n·E(k)\\ F(\theta +n\pi ,k)=F(\theta ,k)+2n·F(k)\end{array}}$

Lo que nos permite calcular los valores de las funciones elípticas para cualquier ángulo conocidos los valores para dichas funciones en el intervalo (0, π/2) y la integral elíptica completa.

Por ejemplo, para la función E(θ,k), obtenemos el valor de E(7π/6,k), conocido el valor de E(π/6,k) y la integral elíptica completa E(k)

k2=3/4;
[~,E]=ellipke(k2);
th=7*pi/6;
n=floor(th/pi);
resto=rem(th,pi);
disp(ellipticE(th,k2))
if resto<pi/2
    disp(ellipticE(resto,k2)+2*n*E)
 else
     disp(ellipticE(resto-pi,k2)+2*(n+1)*E)
 end
  
fplot(@(x) ellipticE(x,k2), [0,2*pi])
line([th,th],[0,5],'lineStyle','--')
line([resto,resto],[0,5],'lineStyle','--')
grid on
xlabel('\theta')
ylabel('E(\theta,k)')
title('Función elíptica E')

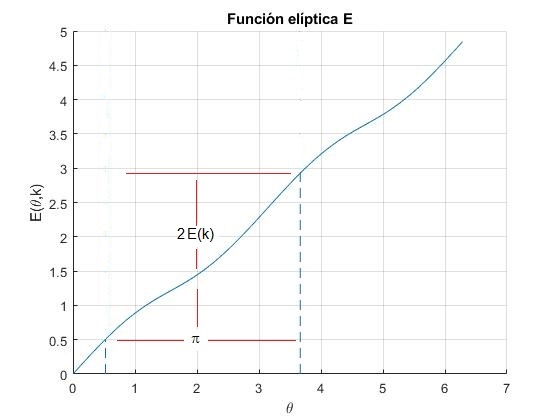
    2.9282
    2.9282

Por ejemplo, para la función F(θ,k), obtenemos el valor de F(5π/6,k), conocido el valor de F(-π/6,k)=-F(π/6,k) y la integral elíptica completa F(k)

k2=3/4;
[K,~]=ellipke(k2);
th=5*pi/6;
n=floor(th/pi);
resto=rem(th,pi);
disp(ellipticF(th,k2))
if resto<pi/2
    disp(ellipticF(resto,k2)+2*n*K)
else
    disp(ellipticF(resto-pi,k2)+2*(n+1)*K)
end

fplot(@(x) ellipticF(x,k2), [-pi/2,2*pi])
line([th,th],[-2,5],'lineStyle','--')
line([resto-pi,resto-pi],[-2,5],'lineStyle','--')
grid on
xlabel('\theta')
ylabel('F(\theta,k)')
title('Función elíptica F')

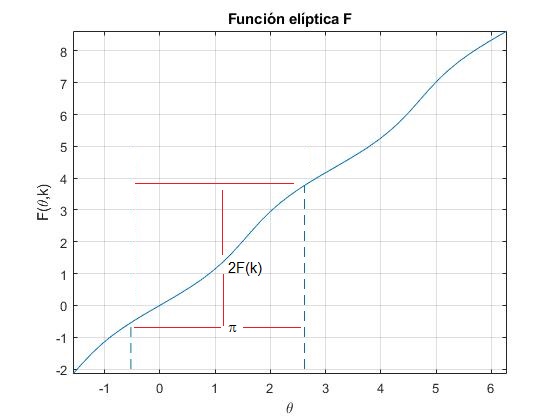
    3.7708
    3.7708

Esta propiedad no tiene utilidad si se trabaja con MATLAB. Para algunas aplicaciones, la podría tener si se utiliza el código de funciones elípticas que han limitado el ángulo al intervalo, 0≤θ≤π/2

Funciones elípticas de Jacobi

Las funciones elípticas de Jacobi sn(x|k), cn(x|k), dn(x|k) se definen del siguiente modo:

${\displaystyle \begin{array}{l}x={\displaystyle \underset{0}{\overset{\theta }{\int }}\frac{d\phi }{\sqrt{1-k^2{\sin }^2\phi }}}0\le \theta \le \frac{\pi }{2}\\ \text{sn}x=\sin \theta \\ \text{cn}x=\cos \theta \\ \text{dn}x=\sqrt{1-k^2{\sin }^2\theta }\end{array}}$

Obtenemos el valor de las funciones sn(x|k), cn(x|k) y dn(x|k), mediante la función ellipj de MATLAB, k²≤1.

• Representamos la función elíptica de Jacobi sn(x|k) para dos valores de k²<1: 0.1 y 0.9

x=linspace(0,10,200);
[sn,~,~]=ellipj(x,0.1);
hold on
plot(x,sn)
[sn,~,~]=ellipj(x,0.9);
plot(x,sn)
hold off
ylim([-1.05,1.05])
xlabel('x')
ylabel('sn(x)')
legend ('0.1','0.9', 'location', 'southwest')
title('Funciones elípticas de Jacobi, sn')
grid on



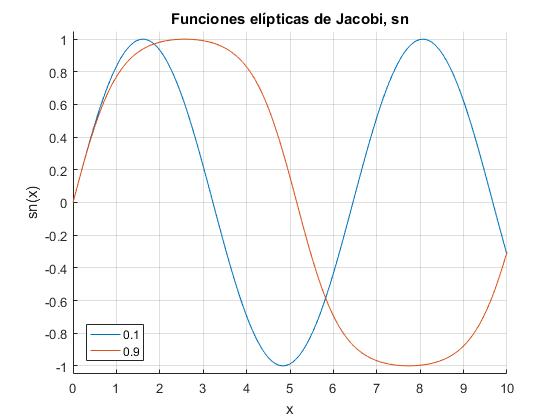
• Representamos la función elíptica de Jacobi cn(x|k) para dos valores de k²<1: 0.1 y 0.9

x=linspace(0,10,200);
[~,cn,~]=ellipj(x,0.1);
hold on
plot(x,cn)
[~,cn,~]=ellipj(x,0.9);
plot(x,cn)
hold off
ylim([-1.05,1.05])
xlabel('x')
ylabel('cn(x)')
legend ('0.1','0.9', 'location', 'southwest')
title('Funciones elípticas de Jacobi, cn')
grid on



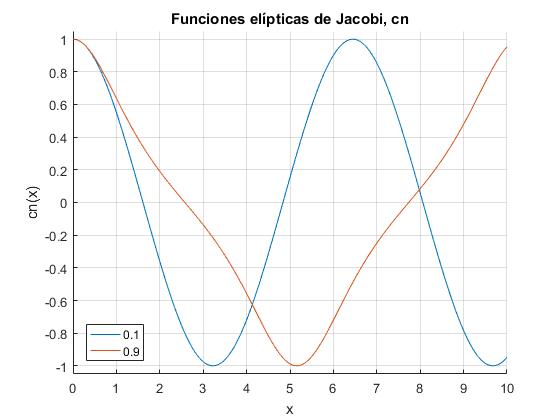
Cuando x=K(k), integral elíptica completa de primera especie, sn(x|k) vale 1. Cuando x=2K(k), sn(x|k)=0. Por lo que 2K(k) es medio periodo, tal como podemos comprobar en las gráficas de las funciones sn(x|k) y cn(x|k)

>> K=ellipke(0.1);
>> [sn,cn,~]=ellipj(2*K,0.1);
>> sn,cn
sn =   1.2246e-16
cn =    -1
>> 2*K
ans =    3.2249

>> K=ellipke(0.9);
>> [sn,cn,dn]=ellipj(2*K,0.9);
>> sn,cn
sn =   1.2246e-16
cn =    -1
>> 2*K
ans =    5.1562

Las funciones sn(x|k) y cn(x|k) están relacionadas, como sus análogas trigonométricas

sn²(x|k)+cn²(x|k)=1

• Representamos la función elíptica de Jacobi dn(x|k) para dos valores de k²<1: 0.1 y 0.9

x=linspace(0,10,200);
[~,~,dn]=ellipj(x,0.1);
hold on
plot(x,dn)
[~,~,dn]=ellipj(x,0.9);
plot(x,dn)
hold off
xlabel('x')
ylabel('dn(x)')
legend ('0.1','0.9', 'location', 'southwest')
title('Funciones elípticas de Jacobi, dn')
grid on



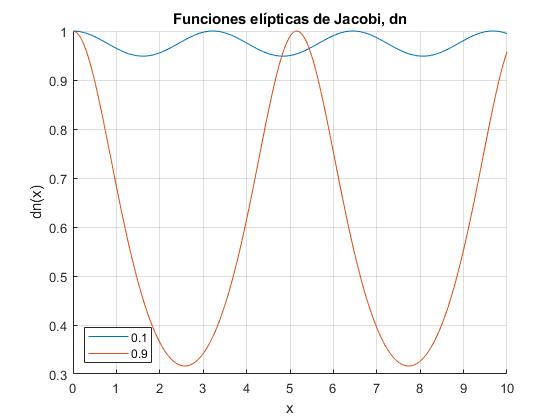
Se trata de una función periódica de periodo 2K(k)

>> K=ellipke(0.1);
>> [~,~,dn]=ellipj(2*K,0.1);
>> dn
dn =     1
>> K=ellipke(0.9);
>> [~,~,dn]=ellipj(2*K,0.9);
>> dn
dn =     1

Valores límite k²

• Para k²=1, las funciones sn(x|1) y cn(x|1) dejan de ser periódicas

x=linspace(0,10,200);
[sn,cn,~]=ellipj(x,1);
hold on
plot(x,sn)
plot(x,cn)
hold off
ylim([-.05,1.05])
xlabel('x')
ylabel('cn(x)')
legend ('sn','cn', 'location', 'southwest')
title('Funciones elípticas de Jacobi, k^2=1')
grid on



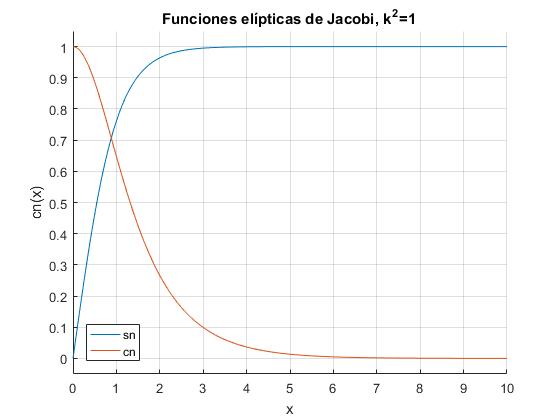
Comprobamos la equivalencia:

sn(x|1)=tanh(x),
cn(x|1)=1/cosh(x),
dn(x|1)=1/cosh(x)

Añadiendo al script, las líneas de código

...
fplot(@(x) tanh(x),[0,10])
fplot(@(x) 1./cosh(x),[0,10])
...

• Para k²=0, las funciones sn(x|k) y cn(x|k) son iguales a sus análogas trigonométricas

sn(x|0)=sin(x),
cn(x|0)=cos(x),
dn(x|0)=1

• Cuando k²>1

Las funciones elípticas se calculan habitualmente para 0≤k²≤1 (es el intervalo que permite MATLAB). Cuando k²>1, es posible calcularlas mediante las relaciones:

${\displaystyle \begin{array}{l}\text{sn}(x|k)=\frac{1}{\sqrt{k}}\text{sn}\left(\sqrt{k}·x|\frac{1}{k}\right)\\ \text{cn}(x|k)=\text{dn}\left(\sqrt{k}·x|\frac{1}{k}\right)\\ \text{dn}(x|k)=c\text{n}\left(\sqrt{k}·x|\frac{1}{k}\right)\end{array}}$

Derivadas

${\displaystyle \begin{array}{l}\frac{d}{dx}\text{sn}(x|k)=\text{cn}(x|k)\text{dn}(x|k)\hfill \\ \begin{array}{l}\frac{d}{dx}\text{cn}(x|k)=-\text{sn}(x|k)\text{dn}(x|k)\\ \frac{d}{dx}\text{dn}(x|k)=-k^2·\text{sn}(x|k)\text{cn}(x|k)\end{array}\hfill \end{array}}$

Vuelta al mundo en un día

Supongamos que partimos del polo Norte y nos movemos sobre la superficie de la Tierra con velocidad constante v.

v=ds/dt, donde ds es la longitud del arco entre dos puntos P y Q sobre la superficie de la Tierra que recorremos en un tiempo dt.

Por otra parte, nos desplazamos con la misma velocidad angular ω de la Tierra, por ejemplo, siempre estamos bajo el Sol, al mediodía. El ángulo (longitud geográfica) φ=ωt. En un día, cruzamos todos los meridianos, dando una vuelta completa a la Tierra.

La trayectoria sobre la superficie de la Tierra que describimos, se denomina espiral de Seiffert, cuyas ecuación, eliminando el tiempo t, depende de un parámetro k.

${\displaystyle \phi =ksk=\frac{\omega }{v}}$

Establecemos coordendas cilíndricas para describir el movimiento. Las coordendas del punto P son (φ, ρ, z), tal como vemos en la figura.

• φ es el ángulo que forma el meriano que pasa por P con el meridiano de referencia
• z es la altura de P sobre el ecuador
• ρ es la distancia del P al eje de rotación Z

Suponiendo que la Tierra es una esfera de radio unidad R=1, se cumple que ρ²+z²=1

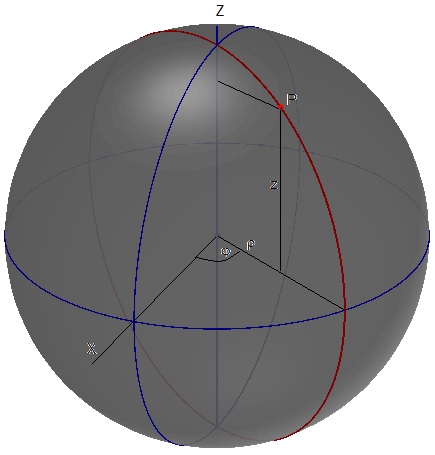
En la figura, se ha dibujado en azul, el meridiano de referencia, el ecuador y el eje de rotación. En rojo, el meridiano que pasa por el punto P, cuyas coordendas cilíndricas (φ, ρ, z). El código empleado para dibujar parte de esta figura, es el siguiente:

hold on

%esfera
R=1; %radio de la Tierra
theta=linspace(0,pi,50);
phi=linspace(0,2*pi,50);
[phi,theta]=meshgrid(phi,theta);
x=R*sin(theta).*cos(phi);
y=R*sin(theta).*sin(phi);
z=R*cos(theta);
h1=surfl(x,y,z);
set(h1,'EdgeColor',[0.6,0.6,0.6],'EdgeAlpha',0.9,'FaceAlpha',0.9)
shading interp
colormap(gray);

%meridiano de referencia
phi=0;
theta=linspace(0,2*pi,100);
x=R*sin(theta).*cos(phi);
y=R*sin(theta).*sin(phi);
z=R*cos(theta);
%trayectoria
h1=line(x,y,z);
set(h1,'Color',[0,0,0.5],'LineWidth',1)

%meridiano de que pasa por el punto P
phi=pi/3;
theta=linspace(0,2*pi,100);
x=R*sin(theta).*cos(phi);
y=R*sin(theta).*sin(phi);
z=R*cos(theta);
%trayectoria
h1=line(x,y,z);
set(h1,'Color',[.5,0,0],'LineWidth',1.5)

%ecuador
phi=linspace(0,2*pi,100);
theta=pi/2;
x=R*sin(theta).*cos(phi);
y=R*sin(theta).*sin(phi);
z=R*cos(theta)*ones(length(x),1);
%trayectoria
h1=line(x,y,z);
set(h1,'Color',[0,0,0.5],'LineWidth',1)

%eje de la Tierra
h1=line([0,0],[0,0],[-1.1,1.1]);
set(h1,'Color',[0,0,0.5],'LineWidth',1)

%punto P
theta=pi/6;
phi=pi/3;
x=R*sin(theta).*cos(phi);
y=R*sin(theta).*sin(phi);
z=R*cos(theta);
%punto P y centro de la esfera
plot3(x,y,z,'ro','linewidth',1,'markersize',4,'markeredgecolor','r',
'markerfacecolor','r')
plot3(0,0,0,'bo','linewidth',1,'markersize',4,'markeredgecolor','b',
'markerfacecolor','b')

view (112,28)
hold off
axis equal
axis off

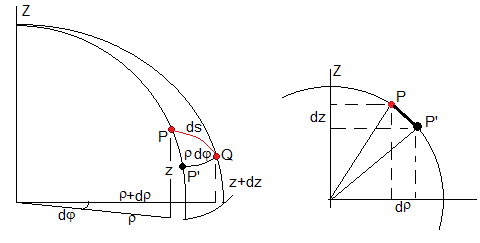
Supongamos que nos movemos sobre la superficie de la Tierra, desde el punto P (φ, ρ, z) al punto muy próximo Q (φ+dφ, ρ+dρ, z+dz), la longitud del arco ds es

${\displaystyle d{s}^2={\rho }^{2}d{\phi }^2+d{\rho }^2+d{z}^2}$

• Teniendo en cuenta que φ=ks y que ρ²+z²=1, escribimos ds en función de ρ y dρ

${\displaystyle \begin{array}{l}d{s}^2={\rho }^2{k}^{2}d{s}^2+\frac{1}{{\rho }^2-1}d{\rho }^2\\ \left(1-{\rho }^2{k}^2\right)d{s}^2=\frac{1}{{\rho }^2-1}d{\rho }^2\\ ds=\frac{d\rho }{\sqrt{\left(1-{\rho }^2{k}^2\right)\left({\rho }^2-1\right)}}\end{array}}$

La longitud del arco s que recorre desde el polo Norte hasta un punto P que dista ρ del eje de rotación es

${\displaystyle s\left(\rho ,k^2\right)={\displaystyle \underset{0}{\overset{\rho }{\int }}\frac{d\rho }{\sqrt{\left(1-{\rho }^2{k}^2\right)\left({\rho }^2-1\right)}}}}$

La inversa de esta función es ρ= sn(s|k)

• Teniendo en cuenta que φ=ks y que ρ²+z²=1, escribimos ds en función de z y dz

${\displaystyle \begin{array}{l}d{s}^2={\rho }^{2}d{\phi }^2+d{\rho }^2+d{z}^2\\ d{s}^2={\rho }^2{k}^{2}d{s}^2+\frac{1}{z^2-1}d{z}^2\\ \left(1-k^2+z^2{k}^2\right)d{s}^2=\frac{1}{z^2-1}d{z}^2\\ ds=\frac{dz}{\sqrt{\left(1-k^2+z^2{k}^2\right)\left(z^2-1\right)}}\end{array}}$

La longitud del arco s que recorre desde el polo Norte hasta un punto P que dista z del plano del ecuador es

${\displaystyle s\left(z,k^2\right)={\displaystyle \underset{0}{\overset{z}{\int }}\frac{dz}{\sqrt{\left(1-k^2+z^2{k}^2\right)\left(z^2-1\right)}}}}$

La inversa de esta función es z= cn(s|k)

Para trazar la espiral para un determinado valor de k², se procede del siguiente modo:

• Dada la longitud del arco s, se obtiene el ángulo φ=s/k
• Se determinan las coordenadas ρ, z del punto P utilizando las funciones sn y cn

ρ= sn(s|k), z= cn(s|k)

Por ejemplo, para k²=1

%esfera
R=1; %radio de la Tierra
phi=linspace(0,pi,30);
theta=linspace(0,2*pi,40);
[phi,theta]=meshgrid(phi,theta);
x=R*sin(phi).*cos(theta);
y=R*sin(phi).*sin(theta);
z=R*cos(phi);
h1=surfl(x,y,z);
set(h1,'EdgeColor',[0.6,0.6,0.6],'EdgeAlpha',0.7,'FaceAlpha',0.7)
shading interp
colormap(gray);
axis equal

k2=1;  %cambiar este valor
s=linspace(0,3*pi,200);
[sn,cn,dn]=ellipj(s,k2);
phi=sqrt(k2)*s;
xp=sn.*cos(phi);
yp=sn.*sin(phi);
zp=cn;
%trayectoria
h1=line(xp,yp,zp);
set(h1,'Color',[.7,0,0],'LineWidth',1.5)
view (130,20)
hold off
axis equal
grid on
xlabel('x')
ylabel('y')
zlabel('z')
title('Espiral de Seiffert')
axis off

Para k²=1, las funciones sn(x|1) y cn(x|1) dejan de ser periódicas, tendiendo hacia el valor 1 y 0, respectivamente, por lo que la espiral parte del polo Norte y tiende asintóticamente, hacia el ecuador

Cuando k²<1, las funciones sn(x|k) y cn(x|k) son periódicas y hemos determinado su periodo 4K(k), siendo K (ellipke en MATLAB), la integral elíptica completa de primera especie

La espiral será una trayectoria cerrada si el punto inicial y final difieren en φ=2nπ, con n=1,2,3... e igual a m periodos de sn o cn para un valor dado de k²

${\displaystyle \frac{2n\pi }{k}=m·4K\left(k\right)m,n=\mathrm{1,2,3...}}$

Dados los números enteros m y n, resolvemos la ecuación transcendente para calcular el valor de k² que hace que la espiral sea una trayectoria cerrada. Sea por ejemplo m=1 y n=1

n=1;
m=1;
f=@(x) 2*n*pi/sqrt(x)-4*m*ellipke(x);
k2=fzero(f, 0.5);
disp(k2)

   0.6284

En el script de la trayectoria cambiamos el valor de la variable k2 a 0.6284, obtiendo la trayectoria cerrada

Referencias

Paul Erdos. Spiraling the Earth with C. G. J. Jacobi. Am. J. Phys. 68 (10) October 2000, pp. 888-895

Ejemplos en el curso de Física

Funciones elípticas: ellipke, ellipticF, ellipticE, ellipticPi, ellipj

Movimiento sobre una cúpula semiesférica

Movimiento sobre una superficie semicircular cóncava

Modelo PREM del interior de la Tierra

Caída de una varilla inclinada

Flexión de una viga en voladizo (II)

Pandeo de una barra delgada empotrada en un extremo

Flexión de una regla

El péndulo simple (II)

El péndulo interrumpido

Oscilador no lineal

Oscilaciones de una esfera que flota en el agua

Campo eléctrico de un sistema de dos o más cargas eléctricas

Campo y potencial eléctrico de una distribución continua de carga

Campo magnético producido por una corriente circular en un punto fuera de su eje

Campo magnético producido por una espira de forma cualesquiera

Circuitos acoplados. Coeficiente de inducción mutua

Una partícula desliza sobre una pista circular que gira

Carga inducida en un conductor esférico

Fuerza sobre un dieléctrico (II)

Movimiento en un pozo doble de potencial