Sistema de cuatro ecuaciones con cuatro incógnitas

${\displaystyle \begin{array}{l}{a}_{11}{x}_1+a_{12}{x}_2+a_{13}{x}_3+a_{14}{x}_4=b_1\\ a_{21}{x}_1+a_{22}{x}_2+a_{23}{x}_3+a_{24}{x}_4=b_2\\ a_{31}{x}_1+a_{32}{x}_2+a_{33}{x}_3+a_{34}{x}_4=b_3\\ a_{41}{x}_1+a_{42}{x}_2+a_{43}{x}_3+a_{44}{x}_4=b_4\end{array}}$

Despejamos x₁ de la primera ecuación

${\displaystyle x_1=\frac{b_1}{a_{11}}-\frac{a_{12}}{a_{11}}{x}_2-\frac{a_{13}}{a_{11}}{x}_3-\frac{a_{14}}{a_{11}}{x}_4}$

y la sustituimos en las restantes, quedando el sistema de tres ecuaciones con tres incógnitas

${\displaystyle \begin{array}{l}{a}_{22}^1{x}_2+a_{23}^1{x}_3+a_{24}^1{x}_4=b_2^1\\ a_{32}^1{x}_2+a_{33}^1{x}_3+a_{34}^1{x}_4=b_3^1\\ a_{42}^2{x}_1+a_{43}^1{x}_3+a_{44}^1{x}_4=b_4^1\end{array}}$

con

${\displaystyle a_{ij}^1=a_{ij}-\frac{a_{i1}{a}_{1j}}{a_{11}}{b}_i^1=b_i-\frac{a_{i1}{b}_1}{a_{11}}(i,j\mathrm{2,3,4})}$

Despejamos, ahora, x₂ de la primera ecuación

${\displaystyle x_2=\frac{b_2^1}{a_{22}^1}-\frac{a_{23}^1}{a_{22}^1}{x}_3-\frac{a_{24}^1}{a_{22}^1}{x}_4}$

y las sustituimos en las dos restantes, quedando un sistema de dos ecuaciones con dos incógnitas.

${\displaystyle \begin{array}{l}{a}_{33}^2{x}_3+a_{34}^2{x}_4=b_3^2\\ a_{43}^2{x}_3+a_{44}^2{x}_4=b_4^2\end{array}}$

con

${\displaystyle a_{ij}^2=a_{ij}^1-\frac{a_{i2}^1{a}_{2j}^1}{a_{22}^1}{b}_i^2=b_i^1-\frac{a_{i2}^1{b}_2^1}{a_{22}^1}(i,j\mathrm{3,4})}$

Despejamos ahora, x₃ de la primera ecuación

${\displaystyle x_3=\frac{b_3^2}{a_{33}^2}-\frac{a_{34}^2}{a_{33}^2}{x}_4}$

y la sustituimos en la ecuación restante,

${\displaystyle a_{44}^3{x}_4=b_4^3}$

con

${\displaystyle a_{ij}^3=a_{ij}^2-\frac{a_{i3}^2{a}_{3j}^2}{a_{33}^2}{b}_i^3=b_i^2-\frac{a_{i3}^2{b}_3^2}{a_{33}^2}(i,j4)}$

Por tanto, el proceso de resolver un sistema lineal de ecuaciones por el método de Gauss se reduce a la construcción de un sistema equivalente que tenga una matriz triangular.

${\displaystyle \begin{array}{l}{a}_{11}{x}_1+a_{12}{x}_2+a_{13}{x}_3+a_{14}{x}_4=b_1\\ a_{22}^1{x}_2+a_{23}^1{x}_3+a_{24}^1{x}_4=b_2^1\\ a_{33}^2{x}_3+a_{34}^2{x}_4=b_3^2\\ a_{44}^3{x}_4=b_4^3\end{array}}$

Ahora vamos obteniendo las incógnitas empezando por la última ecuación y terminando en la primera.

${\displaystyle \begin{array}{l}{x}_4=\frac{b_4^3}{a_{44}^3}\\ x_3=\frac{b_3^2-a_{34}^2{x}_4}{a_{33}^2}\\ x_2=\frac{b_2^1-a_{23}^1{x}_3-a_{24}^1{x}_4}{a_{22}^1}\\ x_1=\frac{b_1-a_{12}{x}_2-a_{13}{x}_3-a_{14}{x}_4}{a_{11}}\end{array}}$

Sistema de n ecuaciones con n incógnitas

Sea un sistema de n ecuaciones con n incógnitas

${\displaystyle \{\begin{array}{l}{a}_{11}{x}_1+a_{12}{x}_2+a_{13}{x}_3+\mathrm{...}+a_{1n}{x}_n=b_1\\ a_{21}{x}_1+a_{22}{x}_2+a_{23}{x}_3+\mathrm{...}+a_{2n}{x}_n=b_2\\ \mathrm{....}\\ a_{n1}{x}_1+a_{n2}{x}_2+a_{n3}{x}_3+\mathrm{...}+a_{nn}{x}_n=b_n\end{array}}$

que convertimos en el sistema equivalente

${\displaystyle \{\begin{array}{l}{a}_{11}{x}_1+a_{12}{x}_2+a_{13}{x}_3+\mathrm{...}+a_{1n}{x}_n=b_1\\ a_{22}^1{x}_2+a_{23}^1{x}_3+\mathrm{...}+a_{2n}^1{x}_n=b_2^1\\ a_{33}^2{x}_3+\mathrm{...}+a_{3n}^2{x}_n=b_3^2\\ \mathrm{....}\\ a_{n-1n-1}^{n-2}{x}_{n-1}+a_{n-1n}^{n-2}{x}_n=b_{n-1}^{n-2}\\ a_{nn}^{n-1}{x}_n=b_n^{n-1}\end{array}}$

donde

${\displaystyle \begin{array}{l}{a}_{ij}^1=a_{ij}-\frac{a_{i1}}{a_{11}}{a}_{1j}{b}_i^1=b_i-\frac{a_{i1}}{a_{11}}{b}_{1}i,j=\mathrm{2...}n\\ a_{ij}^2=a_{ij}^1-\frac{a_{i2}^1}{a_{22}^1}{a}_{2j}^1{b}_i^2=b_i^1-\frac{a_{i2}^1}{a_{22}^1}{b}_2^{1}i,j=\mathrm{3...}n\\ a_{ij}^k=a_{ij}^{k-1}-\frac{a_{ik}^{k-1}}{a_{kk}^{k-1}}{a}_{kj}^{k-1}{b}_i^k=b_i^{k-1}-\frac{a_{ik}^{k-1}}{a_{kk}^{k-1}}{b}_k^{k-1}i,j=k\mathrm{...}n\\ k=\mathrm{1,2...}n-1\end{array}}$

Obtenemos las incógnitas x_na x₁

${\displaystyle x_n=\frac{b_n^{n-1}}{a_{nn}^{n-1}}{x}_i=\frac{b_i^{i-1}-{\displaystyle \sum _{i+1}^n{a}_{ij}^{i-1}{x}_j^{i-1}}}{a_{ii}^{i-1}}i=n-\mathrm{1,}n-\mathrm{2,...2,1}}$

function x=gauss_ecuacion(A,b)
    Ab=[A b];
    n=length(b);
%matriz triangular
    for k=1:n-1 
        for i=k+1:n
            factor=Ab(i,k)/Ab(k,k);
            for j=k:n+1
                Ab(i,j)=Ab(i,j)-factor*Ab(k,j);
            end
        end
    end
    
%incógnitas
    x=zeros(n,1);
    x(n)=Ab(n,n+1)/Ab(n,n);
    for i=n-1:-1:1 
        x(i)=Ab(i,n+1)/Ab(i,i);
        for j=i+1:n
            x(i)=x(i)-Ab(i,j)*x(j)/Ab(i,i); 
        end
    end
end

Reducimos el código suprimiendo el bucle de índice j y sustituyéndolo por el operador :

function x=gauss_ecuacion(A,b)
    Ab=[A b];
    n=length(b);
%matriz triangular
    for k=1:n-1 
        for i=k+1:n
            factor=Ab(i,k)/Ab(k,k);
            Ab(i,k:n+1)=Ab(i,k:n+1)-factor*Ab(k,k:n+1);          
        end
    end
    
%incógnitas
    x=zeros(n,1);
    x(n)=Ab(n,n+1)/Ab(n,n);
    for i=n-1:-1:1 
        x(i)=Ab(i,n+1)/Ab(i,i)-Ab(i,i+1:n)*x(i+1:n)/Ab(i,i); 
    end
end

Probamos la función gauss_ecuacion con los sistemas de ecuaciones

${\displaystyle \begin{array}{l}\{\begin{array}{l}{x}_1+2x_2+3x_3=6\\ 2x_1+2x_2+3x_3=7\\ x_1+4x_2+4x_3=9\end{array}\\ \{\begin{array}{l}{x}_1+x_2+x_3=4\\ 2x_1+x_2+3x_3=7\\ 3x_1+x_2+6x_3=2\end{array}\end{array}}$

>> A=[1,2,3;2,2,3;1,4,4];
>> b=[6;7;9];
>> gauss_ecuacion(A,b)
ans =
     1
     1
     1
>> A=[1,1,1;2,1,3;3,1,6];
>> b=[4;7;2];
>> gauss_ecuacion(A,b)
ans =
    19
    -7
    -8

Mejora del procedimiento de Gauss

Sea el sistema de ecuaciones

${\displaystyle \{\begin{array}{l}{a}_{11}{x}_1+a_{12}{x}_2+a_{13}{x}_3+\mathrm{...}+a_{1n}{x}_n=b_1\\ a_{21}{x}_1+a_{22}{x}_2+a_{23}{x}_3+\mathrm{...}+a_{2n}{x}_n=b_2\\ \mathrm{....}\\ a_{n1}{x}_1+a_{n2}{x}_2+a_{n3}{x}_3+\mathrm{...}+a_{nn}{x}_n=b_n\end{array}}$

El procedimiento de Gauss no se puede aplicar si a₁₁ es nulo. La solución a este problema es intercambiar filas hasta conseguir que a₁₁≠0. A este elemento a₁₁ que aparece como denominador se le denomina elemento pivote. Si después de la primera iteración

${\displaystyle \begin{array}{l}\{\begin{array}{l}{a}_{11}{x}_1+a_{12}{x}_2+a_{13}{x}_3+\mathrm{...}+a_{1n}{x}_n=b_1\\ a_{22}^1{x}_2+a_{23}^1{x}_3+\mathrm{...}+a_{2n}^1{x}_n=b_2^1\\ a_{32}^1{x}_2+a_{33}^1{x}_3+\mathrm{...}+a_{3n}^1{x}_n=b_3^1\\ \mathrm{....}\\ a_{n2}^1{x}_2+a_{n3}^1{x}_3+\mathrm{...}+a_{nn}^1{x}_n=b_n^1\end{array}\\ a_{22}^1\ne 0\end{array}}$

el primer elemento de la segunda fila (pivote) es nulo hay que intercambiar filas entre las n-1 ecuaciones restantes para que este elemento sea distinto de cero.

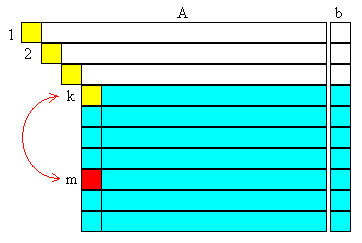
Para mejorar la estabilidad del método de Gauss en cada una de las interacciones se intercambian filas para conseguir que el elemento pivote sea el elemento mayor (en valor absoluto) de cada una de las columnas, es decir que los elementos:

${\displaystyle a_{11},a_{22}^1,a_{33}^2\mathrm{...}{a}_{kk}^{k-1}k=\mathrm{1,2,...}n-1}$

sean lo más grandes (en valor absoluto).

${\displaystyle \{\begin{array}{l}0x_1+4x_2-2x_3-2x_4=-4\\ 1x_1+2x_2+4x_3-3x_4=5\\ -3x_1-3x_2+8x_3-2x_4=7\\ -1x_1+1x_2+6x_3-3x_4=7\end{array}}$

Creamos el siguiente script para ver el proceso de intercambio de filas y de reducción de la matriz A a una matriz triangular.

A=[0,4,-2,-2;1,2,4,-3;-3,-3,8,-2;-1,1,6,-3];
b=[-4;5;7;7];
Ab=[A b]
n=length(b);
for k=1:n-1 
    [mayor,j]=max(abs(Ab(k:n,k)));
    fila=j+k-1;
    if fila~=k
        fprintf('intercambio fila %i por fila %i\n',k,fila);
        Ab([k,fila],:)=Ab([fila,k],:);%intercambio de filas
        Ab %muestra la matriz
    end
    %convierte en matriz triangular
    for i=k+1:n
        factor=Ab(i,k)/Ab(k,k);
        Ab(i,k:n+1)=Ab(i,k:n+1)-factor*Ab(k,k:n+1);          
    end
    Ab %muestra la matriz
end

En la ventana de comandos vemos lo siguiente:

%matriz ampliada Ab
%El elemento pivote Ab(1,1) es cero
Ab =
             0          4.00         -2.00         -2.00         -4.00
          1.00          2.00          4.00         -3.00          5.00
         -3.00         -3.00          8.00         -2.00          7.00
         -1.00          1.00          6.00         -3.00          7.00

intercambio fila 1 por fila 3
Ab =
         -3.00         -3.00          8.00         -2.00          7.00
          1.00          2.00          4.00         -3.00          5.00
             0          4.00         -2.00         -2.00         -4.00
         -1.00          1.00          6.00         -3.00          7.00
%se hacen ceros los elementos de la primera columna de las filas 2,3,4
Ab =
         -3.00         -3.00          8.00         -2.00          7.00
             0          1.00          6.67         -3.67          7.33
             0          4.00         -2.00         -2.00         -4.00
             0          2.00          3.33         -2.33          4.67
%se examinan los valores de los elementos de la segunda columna de las filas 2,3,4
intercambio fila 2 por fila 3
Ab =
         -3.00         -3.00          8.00         -2.00          7.00
             0          4.00         -2.00         -2.00         -4.00
             0          1.00          6.67         -3.67          7.33
             0          2.00          3.33         -2.33          4.67
%se hacen ceros los elementos de la segunda columna de las filas 3,4
Ab =
         -3.00         -3.00          8.00         -2.00          7.00
             0          4.00         -2.00         -2.00         -4.00
             0             0          7.17         -3.17          8.33
             0             0          4.33         -1.33          6.67
%se examinan los valores de los elementos de la tercera columna de las filas 3,4
%no hay intercambio
%se hacen ceros los elementos de la tercera columna de la fila 4
%se completa la matriz triangular
Ab =
         -3.00         -3.00          8.00         -2.00          7.00
             0          4.00         -2.00         -2.00         -4.00
             0             0          7.17         -3.17          8.33
             0             0             0          0.58          1.63

Modificamos la función gauss_ecuacion para incluir la mejora

function x=gauss_ecuacion(A,b)
    Ab=[A b];
    n=length(b);
%matriz triangular
  for k=1:n-1 
        [mayor,j]=max(abs(Ab(k:n,k)));
        fila=j+k-1;
        if fila~=k
            Ab([k,fila],:)=Ab([fila,k],:);%intercambio de filas
        end
        for i=k+1:n
            factor=Ab(i,k)/Ab(k,k);
            Ab(i,k:n+1)=Ab(i,k:n+1)-factor*Ab(k,k:n+1);          
        end
    end
%incógnitas
    x=zeros(n,1);
    x(n)=Ab(n,n+1)/Ab(n,n);
    for i=n-1:-1:1 
        x(i)=Ab(i,n+1)/Ab(i,i)-Ab(i,i+1:n)*x(i+1:n)/Ab(i,i); 
    end
end

Llamamos a la función gauss_ecuacion para resolver el sistema de cuatro ecuaciones lineales

>> A=[0,4,-2,-2;1,2,4,-3;-3,-3,8,-2;-1,1,6,-3];
>> b=[-4;5;7;7];
>> gauss_ecuacion(A,b)
ans =
    0.6000
    1.6000
    2.4000
    2.8000