Funciones MATLAB para calcular las raíces de una ecuación

Raíces de un polinomio, roots

Para calcular las raíces de la ecuación

a₁xⁿ+a₂x^n-1+...+a_nx+a_n+1=0

se emplea la función roots y se le pasa el vector p formado por los coeficientes del polinomio. La función roots devuelve un vector columna que contiene las raíces.

>> p=[a₁ a₂ ... a_n a_n+1];
>> x=roots(p)

La función roots tiene una función inversa poly que se le pasa el vector x que contiene las raíces y devuelve los coeficientes del polinomio

p=poly(x)

Sea f(x)= x⁵- 3.5x⁴ + 2.75x³ + 2.125x² - 3.875x + 1.25

Guardamos los coeficientes del polinomio en el vector fila p=[1 -3.5 2.75 2.125 -3.875 1.25];

Mediante la función plolyval, podemos calcular el valor del polinomio cuando proporcionamos el valor de x

>> p=[1 -3.5 2.75  2.125 -3.875 1.25];
>> polyval(p,  1.5) %valor del polinomio cuando se proporciona el valor de x.
   ans= -0.6250
>> r=roots(p)  %raíces del polinomio
 r =
  2.0000
 -1.0000
 1.0000 + 0.5000i
 1.0000 - 0.5000i
 0.5000
>> p1=poly(r) %reconstruimos el polinomio a partir de las raíces
p1 =    1.0000   -3.5000    2.7500    2.1250   -3.8750    1.2500

Comprobamos que las raíces calculadas son correctas utilizando la función polyval, pasándole los coeficientes del polinomio p y el valor x_i de cada una de las raíces

>> polyval(p,2)
ans =     0

Como ejercicio se sugiere al lector, hallar las raíces de las ecuaciones siguientes con la función roots y reconstruir el polinomio con la función poly, o calcular el valor del polinomio para cada una de las raíces con la función polyval

x³ + x² + x + 1 = 0
x⁵+x²-2x-4=0
x⁵-x⁴ + x³ +2x²-1

Procedimiento gráfico, ginput

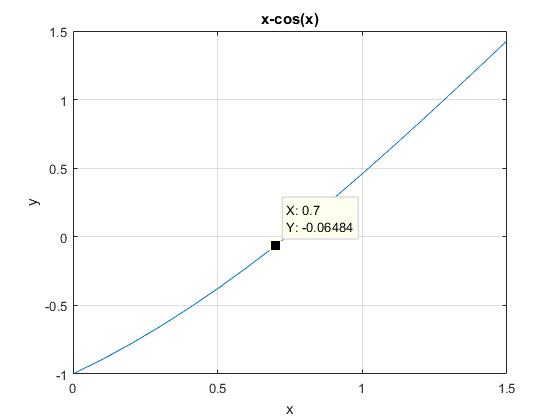
Vamos a estudiar varios procedimientos para calcular la raíz de una ecuación trascedente, por ejemplo, x-cos(x)=0

En primer lugar, vamos a hacer una representación gráfica de esta función para conocer aproximadamente el punto donde la función corta al eje X.

x=0:0.1:pi/2;
y=x-cos(x);
plot(x,y)
grid on
xlabel('x')
ylabel('y')
title('x-cos(x)')

Se selecciona en el menú Tools/Data Cursor, o el icono de la barra horizontal de herramientas. Situamos el cursor en forma de cruz próximo a la raíz de la función y podemos leer sus coordenadas. Cuanto mejor sea la resolución de la gráfica más cerca podremos estar de la raíz buscada. La resolución de la gráfica es el paso Δx utilizado, para calcular la tabla de valores (x, y) en el intervalo que va desde x_i hasta x_f . En este ejemplo Δx=0.1

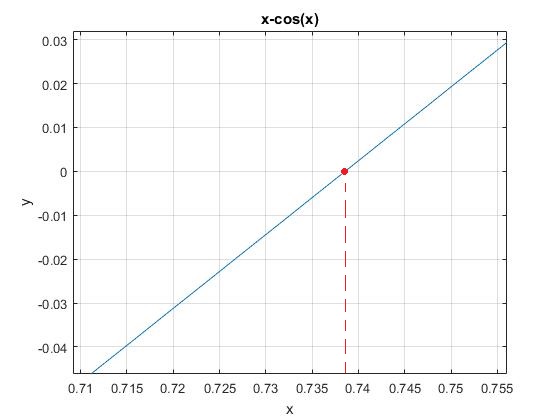
Utilizamos la herramienta Zoom In y Pan para acercarnos a este punto y el botón Zoom Out para alejarnos y volver a la situación inicial. En la imagen podemos ver que después de acercarnos repetidamente al punto de corte con el eje X mediante Zoom In y la mano Pan, la raíz buscada está comprendida entre 0.735 y 0.74.

Raíces simples

Utilizamos el puntero del ratón para buscar los puntos en los que la función corta al eje X, añadiendo el comando ginput al final del script

x=0:0.1:pi/2;
y=x-cos(x);
plot(x,y)
grid on
xlabel('x')
ylabel('y')
title('x-cos(x)')
[xRaiz,yRaiz] = ginput

En la ventana de comandos corremos el script. La raíz buscada se señala mediante el cursor en forma de cruz de color negro. Se pulsa el botón izquierdo del ratón y luego la tecla Retorno.

xRaiz =     0.7379
yRaiz =   -0.0022

Raíces múltiples

Si la función tiene más de una raíz, se señala cada uno de los puntos de intersección de la función con el eje X con el puntero del ratón y se pulsa el botón izquierdo del ratón. Finalmente, se pulsa Retorno y aparecen las abscisas en el vector xRaiz y las ordenadas en el vector yRaiz de dichos puntos.

Nos aproximaremos a las raíces que ya conocemos de una función para ilustrar este interesante procedimiento gráfico

Modificamos el script para representar la función coseno con el eje horizontal en grados y lo guardamos mediante File/Save o pulsando el icono correspondiente.

Las dos raíces de cos(x)=0 en el intervalo (0,360) son 90° y 270°.

x=0:1:360;
y=cosd(x);
plot(x,y)
grid on
xlabel('x')
ylabel('y')
title('cos(x)')
[xRaiz,yRaiz] = ginput

En la ventana de comandos corremos el script. En la ventana gráfica, pulsamos dos veces el botón izquierdo del ratón:

cuando el puntero está situado aproximadamente en el punto de coordendas (90,0), pulsamos el botón izquierdo del ratón
cuando el puntero está situado en el punto (270,0), pulsamos el botón izquierdo del ratón
pulsamos Retorno,

y obtenemos lo siguiente:

>> mouse_raiz_1
xRaiz =  89.8618  270.5069 
yRaiz =  -0.0088    -0.0029

El procedimiento gráfico nos da una estimación de las raíces (puntos de intersección en la representación gráfica de la función con el eje X) de una ecuación trascendente en un intervalo (a,b) dado.

La función fzero

La función fzero puede encontrar la raíz de una ecuación trascendente f(x)=0. Su sintaxis es

fzero(funcion,[a,b])
fzero(funcion,x0)

Donde funcion es el nombre de la función cuyas raíces queremos determinar y [a,b] es el intervalo donde la función cambia de signo, es decir, el signo de f(a) es distinto al signo de f(b). Alternativamente, se le pude pasar x0, un valor cercano a la raíz es decir, una primera aproximación. Definimos una función anónima func que le pasamos a fzero.

En la ventana de comandos, definimos la función y buscamos un intervalo [0.4,1] donde la función cambia de signo. Alternativamente, probamos una primara aproximación a la raíz buscada x0=0.6

>> func=@(x) cos(x)-x;
>> func(0.4)
ans =   0.5211
>> func(1)
ans =    -0.4597
>> r=fzero(func,[0.4 1]) %intervalo donde se encuentra la raíz
r= 0.7391
>> fzero(func,0.6) %aproximación inicial a la raíz
ans =    0.7391

Definimos explícitamente la función func y la guardarmos en el fichero func.m

function y=func(x) 
     y=cos(x)-x; 
end

Llamamos a fzero anteponiendo al nombre de la función el símbolo @

>> fzero(@func,0.6)
ans= 0.7391

A veces la función func definida y guardada en un fichero .m precisa de los valores de ciertos parámetros a, b

function y=func(x,a,b)
%código de la función
end

A fzero solamente le podemos pasar el manejador (handle) de la función de variable x. La forma en que la función func conoce el valor de sus parámetros a y b es crear una función anónima f1 en términos de func y se le pasamos su manejador a la función fzero

f1=@(x)func(x,a,b);
p=fzero(f1,x0);

Ejemplo

Consideremos el siguiente mecanismo formado por tres barras articuladas. Conocidas las longitudes de las barras r₂, r₃ y r₄ y la distancia r₁ entre la primera articulación y la última queremos relacionar los ángulos α y φ. Como vemos en el dibujo, el vector ${\vec{r}}_{1} = {\vec{r}}_{2} + {\vec{r}}_{3} + {\vec{r}}_{4}$ es la suma de los otros tres.

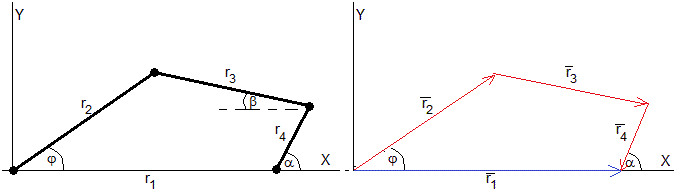
${\begin{cases} r_{2} \cos φ + r_{3} \cos β - r_{4} \cos α = r_{1} \\ r_{2} \sin φ = r_{3} \sin β + r_{4} \sin α \end{cases}$

Eliminamos el ángulo β, despejando r₃cosβ en la primera ecuación, r₃sinβ en la segunda ecuación, elevando al cuadrado ambas ecuaciones y sumando

$\frac{r_{1}^{2} + r_{2}^{2} + r_{4}^{2} - r_{3}^{2}}{2 r_{2} r_{4}} + \frac{r_{1}}{r_{2}} \cos α - \frac{r_{1}}{r_{4}} \cos φ - \cos (α - φ) = 0$

Conocidos r₁, r₂, r₃ y r₄, dado el ángulo α se obtiene el ángulo φ

r1=10;r2=6;r3=8;r4=4;
a=(r1^2+r2^2+r4^2-r3^2)/(2*r2*r4);
alfa=120*pi/180;
f=@(x) a+r1*cos(alfa)/r2-r1*cos(x)/r4-cos(alfa-x);
phi=fzero(f,[0,pi]);
disp([alfa*180/pi, phi*180/pi])
x=[0,r2*cos(phi), r1+r4*cos(alfa), r1];
y=[0,r2*sin(phi), r4*sin(alfa), 0];
plot(x,y, '-ro', 'lineWidth',2, 'markersize',6,'markeredgecolor',
'b','markerfacecolor','b')
line([0,r1],[0,0], 'color','k')
axis off

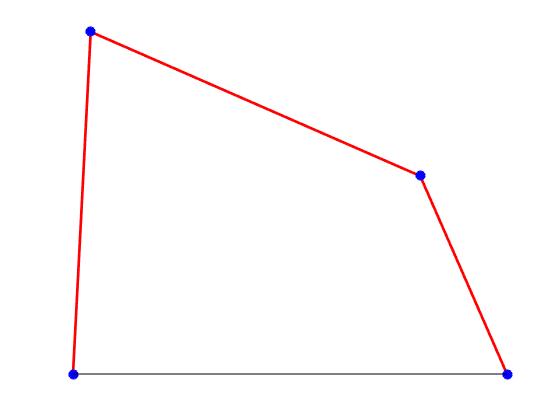
  120.0000   86.1015

Raíces múltiples

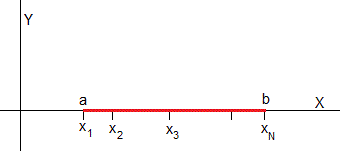
En la página anterior hemos definido una función buscar_intervalos que devuelve los intervalos en los que la función cambia de signo. Una vez conocidos estos intervalos aplicamos un procedimiento numérico, por ejemplo, el del punto medio para calcular la raíz de la función en el intervalo considerado. En el código de la función buscar_intervalos vemos que la matriz xb va creciendo a medida que se añaden intervalos.

Vamos a definir una función raices a la que se le pasa la función f cuyas raíces queremos calcular en un intervalo dado (a,b) y un vector x que contiene los extremos del intervalo y varias abscisas a<x_i<b pertenecientes a dicho intervalo, tal como vemos en la figura. La función MATLAB find identifica aquellos intervalos en los que la función f cambia de signo. La función raices devuelve el vector r de las raíces de la función f en el intervalo (a,b)

function r = raices(f, x)
    y=f(x);
    indices=find(y(1:end-1).*y(2:end)<0);
    r=zeros(1,length(indices));
    for k=1:length(indices)
        r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
    end
end

Calculamos las raíces de la función de Bessel besselj(1,x) en el intervalo que va de a=0.1 y b=30 que son los primeros mínimos de la intensidad de la difracción producida por una apertura circular. Se omite la primera raíz x=0 por que corresponde al máximo principal.

>> J1=@(x) besselj(1,x);
>> x=linspace(0.1,30,50);
>> raices(J1,x)'
ans =
    3.8317
    7.0156
   10.1735
   13.3237
   16.4706
   19.6159
   22.7601
   25.9037
   29.0468

Supongamos ahora que una función cos_a que depende de un parámetro a

function z = cos_a(x,a)
    z=cos(a*x);
end

Calculamos las raíces de esta ecuación para el valor del parámetro a=2 en el intervalo (0,2π)

>> a=2;
>> f=@(x) cos_a(x,a);
>> x=linspace(0,2*pi,10);
>> raices(f,x)
ans =    0.7854    2.3562    3.9270    5.4978

Mínimo de una función

Cuando se estudia una función f(x), no solamente son relevantes los ceros, sino también los máximos y mínimos locales. La función fminbnd calcula el mínimo de una función en el intervalo (a,b). Un máximo local es el mínimo en el mismo intervalo de la función -f(x), basta por tanto, multiplicar la función f(x) por -1. Por ejemplo, cos(x) tiene un mínimo en x=π. sin(x) tiene un máximo en x=π/2

>> fminbnd(@cos,0,2*pi)
ans =    3.1416
>> f=@(x) -sin(x);
>> fminbnd(f,0,2*pi)
ans =    1.5708

Si representamos la función y=1-xe^-x, en el intervalo (0,5), veremos que tiene un mínimo en x=1, que podemos determinar con la función fminbnd

>> f=@(x) 1-x*exp(-x);
>> fplot(f,[0,5])
>> fminbnd(f,0,5)
ans =    1.0000

Ejemplos en el curso de Física

Se dispara un proyectil contra un blanco móvil

Movimiento sobre una superficie semicircular cóncava

Movimiento sobre una superficie cóncava en forma de cicloide

Movimiento sobre una superficie parabólica

Movimiento del extremo de una cadena bajo la acción de un fuerza constante

Estudio del movimiento de una cadena con una máquina de Atwood

Movimiento de una partícula atada a una cuerda que se enrolla en un cilindro horizontal.

Rozamiento en el bucle

Flexión de una viga en voladizo (II)

Movimiento de un carrete que rueda

Pandeo de una barra delgada empotrada en un extremo

Difracción producida por una rendija

Difracción Fraunhofer producida por una abertura circular

Modos normales de vibración de una barra elástica

Modos de vibración de una cuerda no homogénea

Modos de vibración de una cuerda con cuentas

Modos normales de un cable en movimiento de rotación, suspendido verticalmente.

Modos de vibración de una membrana circular

La ecuación de van der Waals

Las leyes del enfriamiento y calentamiento

Medida de la viscosidad de un fluido

Fuerza de rozamiento proporcional a la velocidad

Fuerza de rozamiento proporcional al cuadrado de la velocidad

Movimiento vertical de una esfera en el seno de un fluido viscoso.

Un globo que asciende en la atmósfera

El electroscopio

Oscilaciones de un cilindro que rueda sobre un plano inclinado con un imán en su interior

Fenómenos capilares

El pozo de potencial

Sistema de pozos de potencial

Potencial periódico. Modelo de Kronig-Penney

La radiación del cuerpo negro