Determinante

Un determinante es un número asociado a una matriz cuadrada. Para una matriz cuadrada de dimensión 2×2

${\displaystyle A=\left[\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right]\left|A\right|=a_{11}{a}_{22}-a_{12}{a}_{21}}$

El determinante de una matriz m×m se desarrolla en términos de una combinación de determinates de matrices de dimensión m-1×m-1 y así, sucesivamente, hasta llegar a los determinantes de matrices 2×2.

Por ejemplo, el determinante de una matriz 3×3 es

${\displaystyle \left|\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32}& a_{33}\end{array}\right|=a_{11}\left|\begin{array}{cc}{a}_{22}& a_{23}\\ a_{32}& a_{33}\end{array}\right|-a_{12}\left|\begin{array}{cc}{a}_{21}& a_{23}\\ a_{31}& a_{33}\end{array}\right|+a_{13}\left|\begin{array}{cc}{a}_{22}& a_3\\ a_{32}& a_{33}\end{array}\right|}$

El determinante se calcula mediante la siguiente fórmula

${\displaystyle \det (A)={\displaystyle \sum _{j=1}^n{(-1)}^{1+j}{a}_{1j}\det (M_{1j})}}$

Donde M_1j es una submatriz obtenida eliminando la fila 1 y la columna j de la matriz A

En la página titulada Matrices hemos visto como se accede a los elementos de una matriz

Tomemos la matriz cuadrada A de dimensión 4×4, la submatriz M12 que se obtiene eliminando la primera fila y la segunda columna es

>> A=[1 2 3 4; 5 6 7 8; 9 10 11 12; 13 14 15 16]
A =
     1     2     3     4
     5     6     7     8
     9    10    11    12
    13    14    15    16

>> M12=[A(2:4,1),A(2:4,3:4)]
M12 =
     5     7     8
     9    11    12
    13    15    16

Definimos la función determinante que toma la matriz A de dimensión n×n y produce matrices M_1j de dimensión n-1×n-1 y calcula el determinante de acuerdo con la fórmula anterior, de forma recursiva

function d = determinante(A)
    n=length(A);
    if n==1;
        d=A(1,1);
    else
        d=0; 
        sgn=1;
        for j=1:n
            M1j=[A(2:n,1:j-1) A(2:n,j+1:n)];
            d=d+sgn*A(1,j)*determinante(M1j);
            sgn=-sgn;
        end
    end
end

Calculamos el determinante de esta matriz utilizando la función determinante

${\displaystyle \left|\begin{array}{ccc}-1& 0& 3\\ 2& -1& 0\\ 3& 1& -2\end{array}\right|=13}$

>> A=[-1 0 3; 2 -1 0; 3 1 -2]
A =
    -1     0     3
     2    -1     0
     3     1    -2
>> determinante(A)
ans =    13

En MATLAB la función det(A) calcula el determinante de la matriz cuadrada A.

>> det(A)
ans = 13

Matriz inversa

Se denomina matriz identidad I a aquella matriz cuadrada de dimensiones m×m en la cual los elementos de la diagonal valen 1 y el resto de los elementos vale cero. MATLAB dispone de la función eye(m) para crear una matriz cuadrada de dimensión m con los elementos de la diagonal principal unos y el resto ceros.

El producto de la matriz identidad I por otra matriz A nos da la matriz A

${\displaystyle \begin{array}{l}A=\left[\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{21}& a_{23}\end{array}\right]I=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]\\ A*I=\left[\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{21}& a_{23}\end{array}\right]\end{array}}$

Si la matriz A es cuadrada, se obtiene el mismo resultado efectuando el producto A*I o I*A

Si A es una matriz cuadrada, B es su matriz inversa si el producto A*B=B*A=I

En MATLAB se puede obtener la matriz inversa de A elevando A a la potencia -1, A^-1 o bien, mediante la función inv(A)

>> A=[-1 0 3; 2 -1 0; 3 1 -2]
A =
    -1     0     3
     2    -1     0
     3     1    -2
>> B=inv(A)
B =
    0.1538    0.2308    0.2308
    0.3077   -0.5385    0.4615
    0.3846    0.0769    0.0769
>> A*B
ans =
    1.0000         0         0
   -0.0000    1.0000   -0.0000
         0   -0.0000    1.0000

Rango de una matriz

El rango de una matriz es el máximo número de filas linealmente independientes. La función rank calcula el rango de una matriz. Sea la matriz A

${\displaystyle A=\left[\begin{array}{cccc}0& -1& 2& 1\\ 1& -1& 0& -1\\ 3& 1& 2& 0\\ 2& -3& 2& -1\end{array}\right]}$

>> A=[0 -1 2 1; 1 -1 0 -1; 3 1 2 0; 2 -3 2 -1];
>> rank(A)
ans =     3

Como podemos apreciar la fila cuatro es combinación lineal de la fila 1 y la fila 2:. a_4j=a_1j+2·a_2j, j=1...4

División por la izquierda y por la derecha

La división por la izquierda se utiliza para resolver la ecuación AX=B. En esta ecuación X es el vector columna de las incógnitas, B es el vector columna de los términos independientes y A es una matriz cuadrada.

${\displaystyle \begin{array}{l}{a}_{11}{x}_1+a_{12}{x}_2+a_{13}{x}_3=b_1\\ a_{21}{x}_1+a_{22}{x}_2+a_{23}{x}_3=b_2\\ a_{31}{x}_1+a_{32}{x}_2+a_{33}{x}_3=b_3\\ \left[\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32}& a_{23}\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]=\left[\begin{array}{c}{b}_1\\ b_2\\ b_3\end{array}\right]\\ AX=B\end{array}}$

A^-1AX=IX=X

De modo que

X=A^-1B

En MATLAB esta última expresión se escribe utilizando el operador división por la izquierda

X=A\B

La división por la derecha se utiliza para resolver la ecuación XC=D. En esta ecuación X y D son vectores fila y C es una matriz cuadrada.

XCC^-1=DC^-1

X=DC^-1 o bien, X=D/C (división por la derecha)

Sistema de ecuaciones lineales

Sistema de n ecuaciones con n incógnitas. Regla de Cramer

Consideremos un sistema de n ecuaciones con n incógnitas cuya solución es única.

${\displaystyle \{\begin{array}{l}{a}_{11}{x}_1+a_{12}{x}_2+\mathrm{....}{a}_{1n}{x}_n=b_1\\ a_{21}{x}_1+a_{22}{x}_2+\mathrm{....}{a}_{2n}{x}_n=b_2\\ \mathrm{....}\\ a_{n1}{x}_1+a_{n2}{x}_2+\mathrm{....}{a}_{nn}{x}_n=b_n\end{array}}$

Llamemos A a la matriz de los coeficientes, cuyo determinate d es distinto de cero

${\displaystyle d=\left|\begin{array}{cccc}{a}_{11}& a_{12}& \mathrm{...}& a_{1n}\\ a_{21}& a_{22}& \mathrm{...}& a_{2n}\\ \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}\\ a_{n1}& a_{n2}& \mathrm{...}& a_{nn}\end{array}\right|\ne 0}$

La regla de Cramer nos dice que cada una de las incógnitas x_j se puede obtener a partir del determinante de la matriz en la que se ha sustituido la columna j de la matriz A por el vector columna de los términos independientes b.

${\displaystyle x_j=\frac{1}{d}\left|\begin{array}{cccccc}{a}_{11}& a_{12}& \mathrm{...}& b_1& \mathrm{...}& a_{1n}\\ a_{21}& a_{22}& \mathrm{...}& b_2& \mathrm{...}& a_{2n}\\ \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}\\ a_{j1}& a_{j2}& \mathrm{...}& b_j& \mathrm{...}& a_{jn}\\ \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}\\ a_{n1}& a_{n2}& \mathrm{...}& b_n& \mathrm{...}& a_{nn}\end{array}\right|}$

Sea el sistema

${\displaystyle \begin{array}{l}3x_1-x_2=5\\ -2x_1+x_2+x_3=0\\ 2x_1-x_2+4x_3=15\\ \left[\begin{array}{ccc}3& -1& 0\\ -2& 1& 1\\ 2& -1& 4\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]=\left[\begin{array}{c}5\\ 0\\ 15\end{array}\right]\end{array}}$

A=[3 -1 0; -2 1 1; 2 -1 4];
b=[5;0;15];
n=length(b);
d=det(A);
x=zeros(n,1);
for i=1:n
    Ab=[A(:,1:i-1),b,A(:,i+1:n)];
    x(i)=det(Ab)/d;
end
disp('Solución')
disp(x);

Solución
    2.0000
    1.0000
    3.0000

Sistema de m ecuaciones con n incógnitas

Sea el sistema

${\displaystyle \begin{array}{l}\{\begin{array}{l}{a}_{11}{x}_1+a_{12}{x}_2+\mathrm{.....}+a_{1n}{x}_n=b_1\\ a_{21}{x}_1+a_{22}{x}_2+\mathrm{.....}+a_{2n}{x}_n=b_2\\ \mathrm{...}\\ a_{m1}{x}_1+a_{m2}{x}_2+\mathrm{.....}+a_{mn}{x}_n=b_m\end{array}\\ \left[\begin{array}{cccc}{a}_{11}& a_{12}& \mathrm{...}& a_{1n}\\ a_{21}& a_{22}& \mathrm{...}& a_{2n}\\ \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}\\ a_{m1}& a_{m2}& \mathrm{...}& a_{mn}\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ \mathrm{...}\\ x_n\end{array}\right]=\left[\begin{array}{c}{b}_1\\ b_2\\ \mathrm{...}\\ b_m\end{array}\right]\end{array}}$

que podemos escribir Ax=b, donde A es una matriz de dimensión m×n, y x y b son dos vectores columna de longitudes n y m respectivamente. Tenemos un sistema de m ecuaciones con n incógnitas.

1. El sistema tiene solución si y solo si el rango de la matriz A es igual al rango de la matriz ampliada A|b. Sistema compatible.
2. Si el rango es igual al número n de incógnitas el sistema tiene una solución única. Sistema compatible determinado
3. Si el rango es menor que el número n de incógnitas entonces hay un número infinito de soluciones. Sistema compatible indeterminado.

Vamos a ver algunos ejemplos:

1.-Sea el sistema de tres ecuaciones con dos incógnitas

${\displaystyle \{\begin{array}{l}2x_1+x_2=3\\ 2x_1-x_2=0\\ x_1-2x_2=4\end{array}}$

En forma matricial se escribe

${\displaystyle \left[\begin{array}{cc}2& 1\\ 2& -1\\ 1& -2\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]=\left[\begin{array}{c}3\\ 0\\ 4\end{array}\right]}$

La matriz A y la matriz ampliada A|b son respectivamente

${\displaystyle A=\left[\begin{array}{cc}2& 1\\ 2& -1\\ 1& -2\end{array}\right]A|b=\left[\begin{array}{ccc}2& 1& 3\\ 2& -1& 0\\ 1& -2& 4\end{array}\right]}$

>> A=[2 1; 2 -1; 1 -2];
>> b=[3;0;4];
>> Ab=[A b]
Ab =
     2     1     3
     2    -1     0
     1    -2     4
>> rank(A)
ans =     2
>> rank(Ab)
ans =     3

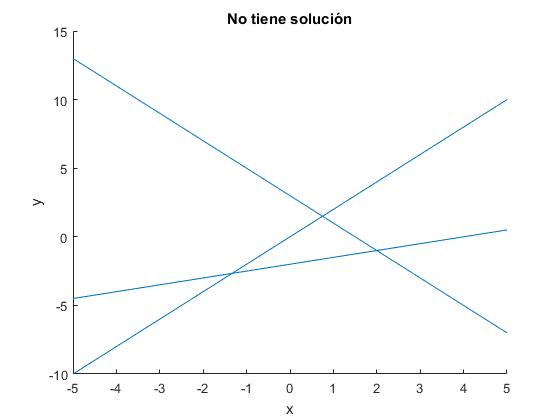
El sistema no tiene solución (primer caso). Cada una de las ecuaciones del sistema representa una recta, identificamos x₁ con x y x₂ con y. En la figura, vemos la representación gráfica de las rectas: y=3-2x, y=2x, y=x/2-2; que como vemos no se cortan en un punto.

line([-5,5],[13,-7])
line([-5,5],[-10,10])
line([-5,5],[-9/2,1/2])
xlabel('x')
ylabel('y')
title('No tiene solución')

2.-Sea el sistema de tres ecuaciones con dos incógnitas

${\displaystyle \begin{array}{l}\{\begin{array}{l}2x_1+x_2=3\\ 4x_1+2x_2=6\\ 6x_1+3x_2=9\end{array}\\ \left[\begin{array}{cc}2& 1\\ 4& 2\\ 6& 3\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]=\left[\begin{array}{c}3\\ 6\\ 9\end{array}\right]\end{array}}$

>> A=[2 1; 4 2; 6 3];
>> b=[3;6;9];
>> Ab=[A b];
>> rank(A)
ans =     1
>> rank(Ab)
ans =     1

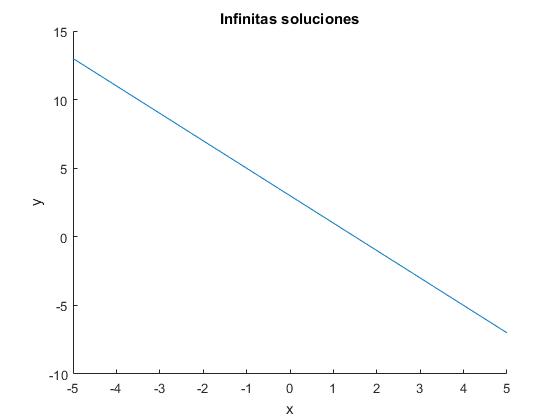
El sistema tiene solución, pero como el rango es menor que el número de incógnitas hay un número infinito de soluciones (tercer caso).

Tenemos tres ecuaciones iguales, la segunda es igual a la primera multiplicada por dos y la tercera es igual a la primera multiplicada por tres. En la figura, se representa la recta y=3-2x, que es la solución del sistema de ecuaciones.

line([-5,5],[13,-7])
xlabel('x')
ylabel('y')
title('Infinitas soluciones')

3.-Sea el sistema de tres ecuaciones con dos incógnitas y su representación matricial

${\displaystyle \begin{array}{l}\{\begin{array}{l}2x_1+x_2=3\\ 2x_1-x_2=5\\ x_1-2x_2=4\end{array}\\ \left[\begin{array}{cc}2& 1\\ 2& -1\\ 1& -2\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]=\left[\begin{array}{c}3\\ 5\\ 4\end{array}\right]\end{array}}$

>> A=[2 1; 2 -1; 1 -2];
>> b=[3;5;4];
>> Ab=[A b];
>> rank(A)
ans =     2
>> rank(Ab)
ans =     2

El sistema tiene solución única ya que el rango es igual al número de incógnitas (segundo caso).

>> X=A\b
X =    2.0000
   -1.0000

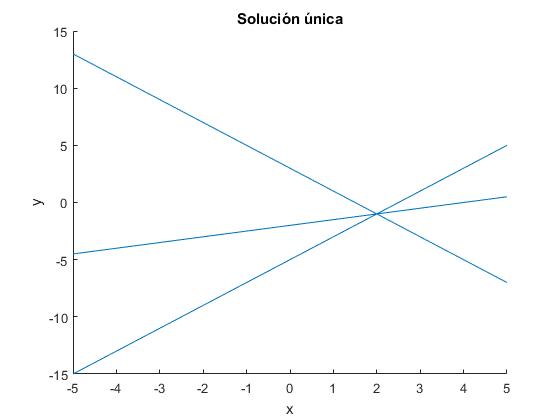
En la figura vemos la representación gráfica de las rectas: y=3-2x, y=2x-5, y=x/2-2; que como vemos se cortan en un el punto x=2, y=-1.

line([-5,5],[13,-7])
line([-5,5],[-15,5])
line([-5,5],[-9/2,1/2])
xlabel('x')
ylabel('y')
title('Solución única')

División por la izquierda \

Vamos a practicar la división por la izquierda \ resolviendo el sistema de tres ecuaciones con tres incógnitas:

${\displaystyle \begin{array}{l}3x_1-x_2=5\\ -2x_1+x_2+x_3=0\\ 2x_1-x_2+4x_3=15\\ \left[\begin{array}{ccc}3& -1& 0\\ -2& 1& 1\\ 2& -1& 4\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]=\left[\begin{array}{c}5\\ 0\\ 15\end{array}\right]\\ AX=B\\ X=A\backslash B\end{array}}$

>> A=[3 -1 0; -2 1 1; 2 -1 4];
>> b=[5;0;15];
>> Ab=[A b];
>> rank(A)
ans =     3
>> rank(Ab)
ans =     3
>> A\b
ans =
    2.0000
    1.0000
    3.0000
>> inv(A)*b
ans =
    2.0000
    1.0000
    3.0000

La función rref

Esta función nos puede ser útil para resolver sistemas de ecuaciones.

• La matriz ampliada Ab del sistema de tres ecuaciones con tres incógnitas del apartado anterior es

${\displaystyle Ab=\left(\overline{)\begin{array}{ccc}3& -1& 0\\ -2& 1& 1\\ 2& -1& 4\end{array}}\begin{array}{c}5\\ 0\\ 15\end{array}\right)}$

>> A=[3 -1 0; -2 1 1; 2 -1 4];
>> b=[5;0;15];
>> Ab=[A b];
>> R=rref(Ab)
R =
     1     0     0     2
     0     1     0     1
     0     0     1     3

Pasamos la matriz Ab a la función rref de MATLAB y obtenemos la matriz ampliada R del sistema equivalente de ecuaciones

${\displaystyle \begin{array}{l}R=\left(\overline{)\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}}\begin{array}{c}2\\ 1\\ 3\end{array}\right)\\ \{\begin{array}{l}{x}_1=2\\ x_2=1\\ x_3=3\end{array}\end{array}}$

• Sea ahora, el sistema de tres ecuaciones con tres incógnitas siguiente:

${\displaystyle \{\begin{array}{l}{x}_1+x_2+x_3=-6\\ x_1-2x_3=4\\ 2x_1+x_2-x_3=18\end{array}}$

Creamos la matriz A de los coeficientes y la matriz ampliada Ab

>> A=[1 1 1;1 0 -2;2 1 -1];
>> b=[-6;4;18];
>> Ab=[A b];
>> R=rref(Ab)
R =
     1     0    -2     0
     0     1     3     0
     0     0     0     1

El sistema equivalente es

${\displaystyle \{\begin{array}{l}{x}_1-2x_3=0\\ x_2+3x_3=0\\ 0=1\end{array}}$

Se trata de un sistema incompatible, tal como podemos comprobar calculando el rango de la matriz A y de su ampliada Ab

>> rank(A)
ans =     2
>> rank(Ab)
ans =     3

• Finalmente, sea el sistema

${\displaystyle \{\begin{array}{l}{x}_1+x_2+x_3=6\\ x_1-2x_3=4\\ 2x_1+x_2-x_3=10\end{array}}$

Creamos la matriz A de los coeficientes y la matriz ampliada Ab

>> A=[1 1 1; 1 0 -2;2 1 -1];
>> b=[6;4;10];
>> Ab=[A b];
>> rref(Ab)
ans =
     1     0    -2     4
     0     1     3     2
     0     0     0     0

La última fila 0x₁+0x₂+0x₃=0 se verifica para cualquier valor de x₁, x₂ y x₃

El sistema equivalente es

${\displaystyle \begin{array}{l}\{\begin{array}{l}{x}_1-2x_3=4\\ x_2+3x_3=2\end{array}\\ \{\begin{array}{l}{x}_1=4+2x_3\\ x_2=2-3x_3\end{array}\end{array}}$

Una solución sería por ejemplo, x₁=4, x₂=2 y x₃=0.

>> rank(A)
ans =     2
>> rank(Ab)
ans =     2

El sistema es compatible e indeterminado.