Método de las aproximaciones sucesivas

El método de las aproximaciones sucesivas es uno de los procedimientos más importantes y más sencillos de codificar. Supongamos la ecuación

f(x)=0

donde f(x) es una función continua que se desea determinar sus raíces reales. Se sustituye f(x) por la ecuación equivalente

x=g(x)

Se estima el valor aproximado de la raíz x₀ y se sustituye en el segundo miembro de la ecuación para obtener x₁.

x₁=g(x₀)

Poniendo x₁ como argumento de g(x), obtendremos un nuevo número x₂ y así, sucesivamente. Este proceso se puede sintetizar en la fórmula.

x_n=g(x_n-1)

Si esta secuencia es convergente es decir, tiende hacia un límite, la raíz buscada ξ es

${\displaystyle \xi =\underset{n\to \infty }{\lim }{x}_n}$

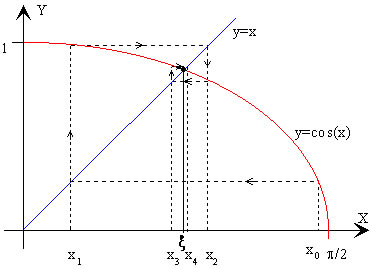
El método de iteración se explica geométricamente mediante el gráfico de la figura. Se dibuja la curva y=g(x), y la recta y=x, bisectriz del primer cuadrante. La abscisa ξ del punto de intersección es la raíz buscada.

Un ejemplo típico, es la de encontrar la raíz de la ecuación x=cos(x)

Para encontrar la raíz, se comienza en el punto cualquiera de abscisa x₀ dentro del intervalo (0, π/2), y se traza la línea vertical hasta que interseca la curva, luego, desde este punto, se traza una línea horizontal hasta que se alcanza la recta bisectriz, este punto tendrá por abscisa x₁. Se traza de nuevo, una línea vertical hasta encontrar a la curva, y otra línea horizontal hasta encontrar la línea recta, el punto de intersección tiene de abscisa x₂ y así, sucesivamente. Como podemos apreciar en la figura, la sucesión x₁, x₂, x₃... tiende hacia la raíz ξ de la ecuación x=cos(x).

Vamos ahora a crear un script para calcular la raíz de la ecuación x=cos(x) en el intervalo 0 a π/2.

Tomamos una aproximación inicial a la raíz x₀, en dicho intervalo y aplicamos la fórmula x_n=g(x_n-1). Su codificación no presenta grandes dificultades.

x=input ('valor inicial: ');
iter=input('número de iteracciones: ');
for i=1:iter;
    x=cos(x);
end
disp(x)

En la ventana de comandos corremos el script y obtenemos una aproximación a la raíz buscada después de 100 iteraciones

valor inicial: 0.5
número de iteracciones: 100
    0.7391

La condición de finalización

Primero, introducimos el valor inicial x, la primera aproximación, calculamos el valor del coseno de x, el valor devuelto (segunda aproximación), lo guardamos de nuevo en la variable x y repetimos el proceso indefinidamente. El código aunque correcto, necesita terminarse en algún momento, cumpliendo una determinada condición.

Cuando el valor absoluto del cociente entre la diferencia de dos términos consecutivos de la sucesión y uno de los términos, sea menor que cierta cantidad ε.

${\displaystyle \left|\frac{x_{n+1}-x_n}{x_{n+1}}\right|<\epsilon }$

Este criterio, no es completamente riguroso, pero es un buen punto de partida para el estudio de este método.

Modificamos el script para sustituir el bucle for por un bucle while indefinido que se interrumpe cuando se cumpla la condición de terminación .

x0=input ('valor inicial: ');
ERROR=0.001;
while(1)  %bucle que se ejecuta indefinidamente
    x=cos(x0);
    if abs((x-x0)/x)<ERROR 
        break
    end
    x0=x;
end
disp(x)

En primer lugar, fijamos el valor de la constante ε o ERROR. Introducimos la primera aproximación a la raíz, y la guardamos en la variable x0, calculamos su coseno y obtenemos la segunda aproximación, la guardamos en la variable x. Verificamos si se cumple la condición de terminación. En el caso de que no se cumpla, x0 toma el valor de x y se repite el proceso. En el momento en que se cumpla la condición de terminación, se sale del bucle indefinido y se imprime la raíz buscada. Como podemos observar las variables x0 y x guardan dos términos consecutivos de la sucesión que tiende hacia la raíz de la función.

Regresamos a la ventana de comandos para correr el script y obtenemos una aproximación a la raíz buscada

valor inicial: 0.5
    0.7387 

El criterio de convergencia

No todas las ecuaciones pueden resolverse por este método, solamente si el valor absoluto de la derivada de la función g(x) en la vecindad de la raíz ξ es menor que la unidad (la pendiente de la recta bisectriz del primer cuadrante es uno). En la figura, podemos ver como es imposible encontrar la solución marcada por un puntito negro en la intersección entre la curva y la recta bisectriz del primer cuadrante, ya que la sucesión x_i diverge.

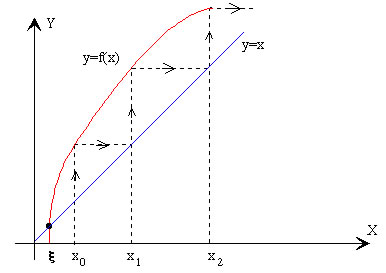
Por ejemplo, la ecuación

x³-x-1=0

tiene una raíz en el intervalo (1, 2) ya que f(1)=-1<0 y f(2)=5>0. Esta ecuación puede escribirse de la forma

x=x³-1

En este caso,

g(x)= x³-1 y su derivada es g'(x)= 3x²

y por tanto,

g'(x)≥3 para 1≤x≤2

en consecuencia, no se cumplen las condiciones de convergencia del proceso de iteración. Si escribimos la ecuación en la forma

${\displaystyle x=\sqrt[3]{x+1}}$

como podrá verificar fácilmente el lector, cumple las condiciones de convergencia, obteniéndose rápidamente un valor aproximado de la raíz buscada mediante el procedimiento de iteracción.

Transformamos el script en una función que denominamos raiz_trascendente para que calcule la raíz de la ecuación x-cos(x)=0

function x=raiz_trascendente(x0, ERROR)
    while(1)
        x=cos(x0);
        if abs((x-x0)/x)<ERROR 
            break
        end
        x0=x;
    end
end

En la ventana de comandos probamos la función raiz_trascendente

>>raiz_trascedente (0.5,0.0001)
ans = 0.7391

Vamos a hacer que este código sea independiente de la función x=g(x) cuya raíz queremos calcular. En el capítulo funciones, ya hemos visto que a una función se le pueden pasar diversos tipos de datos.

Modificamos la definición de la función raiz_trascendente y le pasamos la función f que definiremos en la ventana de comandos, en su primer parámetro y a continuación, la aproximación inicial x0 y el error o tolerancia en la raíz buscada.

function x=raiz_trascendente(f,x0,ERROR)
    while(1)
        x=f(x0);
        if abs((x-x0)/x)<ERROR 
            break
        end
        x0=x;
    end
end

En la ventana de comandos, definimos la función anónima g(x) y calculamos la raíz de la ecuación trascendente x=g(x).

>> g=@(x) cos(x)
>> raiz_trascendente(g,0.5,0.001)
ans =  0.7393

Para aplicar el método de las aproximaciones sucesivas hemos de escribir la ecuación f(x)=0 como x=g(x) y deberán además, cumplirse las condiciones de convergencia en el proceso de iteracción.

Ejemplo en el curso de Física

Velocidad límite constante de una gota de agua que cae en el aire

Método de Newton-Raphson

El desarrollo en serie de la función f(x) en el punto x es

${\displaystyle f(x+h)=f(x)+h·f\text{'}(x)+\mathrm{...}}$

Si h es pequeño, podemos despreciar los términos en h² y superiores. Si x+h es la raíz de la ecuación, entonces f(x+h)=0,

${\displaystyle h\approx -\frac{f(x)}{f\text{'}(x)}}$

Para calcular la raíz mediante un proceso iterativo de la siguiente forma

${\displaystyle x_{n+1}=x_n-\frac{f(x_n)}{f\text{'}(x_n)}}$

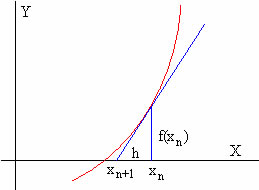
Definimos el procedimiento de Newton-Raphson de un modo similar al de las aproximaciones sucesivas

function x=newton_raphson(f,f_prima,x0,ERROR)
    while(1)
        x=x0-f(x0)/f_prima(x0);
        if abs((x-x0)/x)<ERROR 
            break
        end
        x0=x;
    end
end

A la función newton_raphson, le pasamos la función f y su derivada f_prima, la aproximación inicial x0 y la tolerancia ERROR.

Consideremos la función f(x)=x-cos(x), cuya derivada es f'(x)=1+sin(x). En la ventana de comandos escribimos

>> func=@(x) x-cos(x);
>> func_prima=@(x) 1+sin(x);
>> newton_raphson(func,func_prima,0.5,0.0001)
ans = 0.7391

En el siguiente ejemplo, vamos a ver como se aproxima gráficamente a la solución.

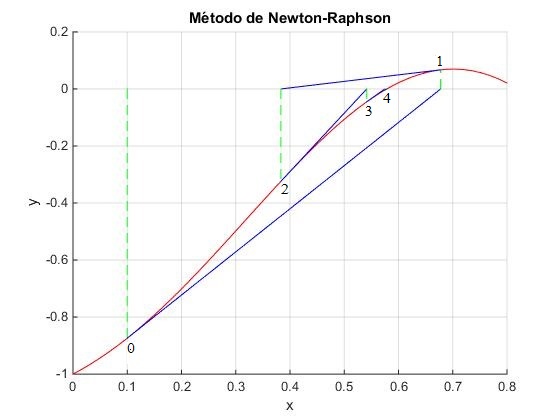
Sea la función y=x·sin(πx)-exp(-x)

Dibujamos la función en color rojo. Probamos con x₀=0.1, trazamos la recta tangente a la curva que pasa por el punto (x₀,y₀), punto señalado en la gráfica con 0. Esta recta corta al eje X en el punto de abscisa x₁. Trazamos la tangente a la curva en el punto (x₁,y₁), punto señalado en la gráfica con 1. Esta recta corta al eje X en el punto de abscisa x₂ y así, sucesivamente.

f=@(x) x.*sin(pi*x)-exp(-x);
fp=@(x) sin(pi*x)+x*pi*cos(pi*x)+exp(-x);

hold on
x=linspace(0,0.8,50);
plot(x,f(x),'r')
x0=0.1;
for i=1:5
    x1=x0-f(x0)/fp(x0);
    h=line([x0,x0],[0,f(x0)],'color','g');
    set(h,'lineStyle', '--')
    line([x1,x0],[0,f(x0)],'color','b')
    x0=x1;
end
hold off
grid on
xlabel('x')
ylabel('y')
title('Método de Newton-Raphson')

Calculamos la raíz

>> f=@(x) x*sin(pi*x)-exp(-x);
>> fp=@(x) sin(pi*x)+x*pi*cos(pi*x)+exp(-x);
>> newton_raphson(f,fp,0.1,0.0001)
ans =    0.5783

Calculamos la derivada de la función aplicando la definición de derivada

${\displaystyle f\text{'}(x)=\underset{\delta \to 0}{\lim }\frac{f(x+\delta )-f(x)}{\delta }}$

Tomamos un valor estimativo de δ=10^-6 que cambiaremos dependiendo del problema. La fórmula de Newton-Raphson se convierte en

${\displaystyle x_{n+1}=x_n-\frac{\delta ·f(x_n)}{f(x_n+\delta )-f(x_n)}}$

function x=newton_raphson_1(f,x0,ERROR)
    DELTA=1.0e-6;
    while(1)
        x=x0-DELTA*f(x0)/(f(x0+DELTA)-f(x0));
        if abs((x-x0)/x)<ERROR 
            break
        end
        x0=x;
    end
end

A la función newton_raphson_1, le pasamos la función f, la aproximación inicial x0 y la tolerancia ERROR. Consideremos la función f(x)=x-cos(x), en la ventana de comandos escribimos

>> func=@(x) x-cos(x);
>> newton_raphson_1(func,0.5,0.0001)
ans = 0.7391

Ejemplo en el curso de Física

El perfil de una gota de rocío

Disco sobre la superficie del agua

Método de la secante

Este método comienza con dos puntos (x₀, f(x₀)) y (x₁, f(x₁)), tales que los signos de f(x₀) y f(x₁) son opuestos, es decir, f(x₀)·f(x₁)<0

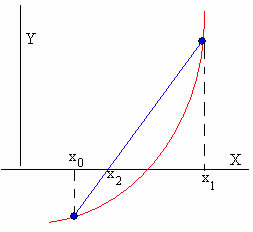
Se dibuja una línea recta entre los dos puntos cuya ecuación es

${\displaystyle \frac{y-f(x_0)}{f(x_1)-f(x_0)}=\frac{x-x_0}{x_1-x_0}}$

El valor de x=x₂ para el cual y se aproxima a la raíz buscada es

${\displaystyle x_2=x_0-f(x_0)\frac{x_1-x_0}{f(x_1)-f(x_0)}}$

En la siguiente iteracción, tomamos un intervalo más pequeño comprendido entre x₂ y x₁ que es donde se encuentra la raíz. Por lo que hacemos x₀=x₂ y volvemos a calcular un nuevo valor x₂ cada vez más próximo a la raíz buscada.

Definimos un nuevo procedimiento denominado secante, se pasa la función f, el intervalo en el que se encuentra la raíz (x0, x1) y el número de iteracciones MAXITER. El procedimiento termina, cuando se encuentra la raíz dentro de una determinada tolerancia

${\displaystyle \left|\frac{a_n-b_n}{m}\right|<{\epsilon }_2}$

donde m=(a_n+b_n)/2 es el punto medio del intervalo (a_n, b_n) cada vez más pequeño.

O bien, cuando se han completado el bucle, sin que se haya encontrado la raíz emitiendo un mensaje de error.

function x2=secante(f,x0,x1,MAXITER)
    ERROR=0.0001;
    for i=1:MAXITER
        f0=f(x0);
        f1=f(x1);
        x2=x0-f0*(x1-x0)/(f1-f0);
        if (abs(2*(x2-x1)/(x2+x1))<ERROR | abs(2*(x2-x0)/(x2+x0))<ERROR)
            break;
        end
        if f(x2)*f0<0
            x1=x2;
        else
            x0=x2;
        end
    end
    if(i==MAXITER) 
        error('no se ha encontrado la raiz')
    end   
end

A la función secante, le pasamos la función f, el intervalo en el que se encuentra la raíz (x0, x1) y el número de iteracciones MAXITER.

Consideremos la función f(x)=cos(x)-x, en la ventana de comandos escribimos

>> func=@(x) cos(x)-x;
>> secante(func,0.5,1,10)
ans = 0.7391