Solución numérica de ecuaciones diferenciales (II)

Sistema de dos ecuaciones diferenciales

Aplicamos el procedimiento numérico de Runge-Kutta para resolver un sistema de dos ecuaciones diferenciales una de primer orden y otra de segundo.

${\begin{cases} \frac{d^{2} x}{d t^{2}} = f (t, x, v_{x}, y) \\ \frac{d y}{d t} = g (t, x, v_{x}, y) \end{cases}$

con las condiciones iniciales

$x (t_{0}) = x_{0}, {(\frac{d x}{d t})}_{t_{0}} = v_{x 0}, y (t_{0}) = y_{0}$

Este sistema, se puede transformar en un sistema equivalente formado por tres ecuaciones diferenciales de primer orden. Obtenemos el esquema descrito en la siguiente tabla

$\frac{d x}{d t} = v_{x}$	$\frac{d v_{x}}{d t} = f (t, x, v_{x}, y)$
$\begin{array}{l} k_{1} = h v_{x} \\ k_{2} = h (v_{x} + \frac{1}{2} l_{1}) \\ k_{3} = h (v_{x} + \frac{1}{2} l_{2}) \\ k_{4} = h (v_{x} + l_{3}) \end{array}$	$\begin{array}{l} l_{1} = h \cdot f (t, x, v_{x}, y) \\ l_{2} = h \cdot f (t + \frac{1}{2} h, x + \frac{1}{2} k_{1}, v_{x} + \frac{1}{2} l_{1}, y + \frac{1}{2} q_{1}) \\ l_{3} = h \cdot f (t + \frac{1}{2} h, x + \frac{1}{2} k_{2}, v_{x} + \frac{1}{2} l_{2}, y + \frac{1}{2} q_{2}) \\ l_{4} = h \cdot f (t + h, x + k_{3}, v_{x} + l_{3}, y + q_{3}) \end{array}$
$x (t + h) = x (t) + \frac{1}{6} (k_{1} + 2 k_{2} + 2 k_{3} + k_{4})$	$v_{x} (t + h) = v_{x} (t) + \frac{1}{6} (l_{1} + 2 l_{2} + 2 l_{3} + l_{4})$
$\frac{d y}{d t} = g (t, x, v_{x}, y)$
$\begin{array}{l} m_{1} = h \cdot g (t, x, v_{x}, y) \\ m_{2} = h \cdot g (t + \frac{1}{2} h, x + \frac{1}{2} k_{1}, v_{x} + \frac{1}{2} l_{1}, y + \frac{1}{2} q_{1}) \\ m_{3} = h \cdot g (t + \frac{1}{2} h, x + \frac{1}{2} k_{2}, v_{x} + \frac{1}{2} l_{2}, y + \frac{1}{2} q_{2}) \\ m_{4} = h \cdot g (t + h, x + k_{3}, v_{x} + l_{3}, y + q_{3}) \end{array}$
$y (t + h) = y (t) + \frac{1}{6} (m_{1} + 2 m_{2} + 2 m_{3} + m_{4})$

Sistema de dos ecuaciones diferenciales de segundo orden

El procedimiento numérico de Runge-Kutta puede aplicarse para resolver un sistema de dos ecuaciones diferenciales de segundo orden que es el caso más frecuente.

${\begin{cases} \frac{d^{2} x}{d t^{2}} = f (t, x, v_{x}, y, v_{y}) \\ \frac{d^{2} y}{d t^{2}} = g (t, x, v_{x}, y, v_{y}) \end{cases}$

con las condiciones iniciales

$x (t_{0}) = x_{0} {(\frac{d x}{d t})}_{t_{0}} = v_{x 0} y (t_{0}) = y_{0} {(\frac{d y}{d t})}_{t_{0}} = v_{y 0}$

Este sistema, se puede transformar en un sistema equivalente formado por cuatro ecuaciones diferenciales de primer orden. Aplicando dos veces el esquema descrito para una ecuación diferencial de segundo orden, obtenemos el esquema descrito en la siguiente tabla

$\frac{d x}{d t} = v_{x}$	$\frac{d v_{x}}{d t} = f (t, x, v_{x}, y, v_{y})$
$\begin{array}{l} k_{1} = h v_{x} \\ k_{2} = h (v_{x} + \frac{1}{2} l_{1}) \\ k_{3} = h (v_{x} + \frac{1}{2} l_{2}) \\ k_{4} = h (v_{x} + l_{3}) \end{array}$	$\begin{array}{l} l_{1} = h \cdot f (t, x, v_{x}, y, v_{y}) \\ l_{2} = h \cdot f (t + \frac{1}{2} h, x + \frac{1}{2} k_{1}, v_{x} + \frac{1}{2} l_{1}, y + \frac{1}{2} q_{1}, v_{y} + \frac{1}{2} m_{1}) \\ l_{3} = h \cdot f (t + \frac{1}{2} h, x + \frac{1}{2} k_{2}, v_{x} + \frac{1}{2} l_{2}, y + \frac{1}{2} q_{2}, v_{y} + \frac{1}{2} m_{2}) \\ l_{4} = h \cdot f (t + h, x + k_{3}, v_{x} + l_{3}, y + q_{3}, v_{y} + m_{3}) \end{array}$
$x (t + h) = x (t) + \frac{1}{6} (k_{1} + 2 k_{2} + 2 k_{3} + k_{4})$	$v_{x} (t + h) = v_{x} (t) + \frac{1}{6} (l_{1} + 2 l_{2} + 2 l_{3} + l_{4})$
$\frac{d y}{d t} = v_{y}$	$\frac{d v_{y}}{d t} = g (t, x, v_{x}, y, v_{y})$
$\begin{array}{l} q_{1} = h v_{y} \\ q_{2} = h (v_{y} + \frac{1}{2} m_{1}) \\ q_{3} = h (v_{y} + \frac{1}{2} m_{2}) \\ q_{4} = h (v_{y} + m_{3}) \end{array}$	$\begin{array}{l} m_{1} = h \cdot g (t, x, v_{x}, y, v_{y}) \\ m_{2} = h \cdot g (t + \frac{1}{2} h, x + \frac{1}{2} k_{1}, v_{x} + \frac{1}{2} l_{1}, y + \frac{1}{2} q_{1}, v_{y} + \frac{1}{2} m_{1}) \\ m_{3} = h \cdot g (t + \frac{1}{2} h, x + \frac{1}{2} k_{2}, v_{x} + \frac{1}{2} l_{2}, y + \frac{1}{2} q_{2}, v_{y} + \frac{1}{2} m_{2}) \\ m_{4} = h \cdot g (t + h, x + k_{3}, v_{x} + l_{3}, y + q_{3}, v_{y} + m_{3}) \end{array}$
$y (t + h) = y (t) + \frac{1}{6} (q_{1} + 2 q_{2} + 2 q_{3} + q_{4})$	$v_{y} (t + h) = v_{y} (t) + \frac{1}{6} (m_{1} + 2 m_{2} + 2 m_{3} + m_{4})$

Definimos la función rk_2_2 que resuelve el sistema de dos ecuaciones diferenciales de segundo orden, cuando le pasamos:

las funciones f(t,x,v_x,y,v_y) y g(t,x,v_x,y,v_y)
las condiciones iniciales: posición inicial (x₀,y₀) y velcidad inicial (v_x0,v_y0) en el instante t₀
el número n de pasos de integración entreel instante inicial t₀ y el final t_f

Nos devuelve los vectores posición (x,y) y velocidad (vx,vy) para cada instante que se guarda en el vector t comprendido entre el instante inicial t0 y el final tf.

function [t,x,vx,y,vy]=rk_2_2(f,g,t0,tf,x0,vx0,y0,vy0,n)
      h=(tf-t0)/n;
      t=t0:h:tf;
      x=zeros(n+1,1); 
%reserva memoria para n+1 element(i)os del vect(i)or x(i)
      y=zeros(n+1,1);
      vx=zeros(n+1,1);
      vy=zeros(n+1,1);
      x(1)=x0; vx(1)=vx0;
      y(1)=y0; vy(1)=vy0;
  
     for i=1:n
        k1=h*vx(i);
        l1=h*f(t(i),x(i),vx(i),y(i),vy(i));
        q1=h*vy(i);
        m1=h*g(t(i),x(i),vx(i),y(i),vy(i));

        k2=h*(vx(i)+l1/2);
        l2=h*f(t(i)+h/2,x(i)+k1/2,vx(i)+l1/2,y(i)+q1/2,vy(i)+m1/2);
        q2=h*(vy(i)+m1/2);
        m2=h*g(t(i)+h/2,x(i)+k1/2,vx(i)+l1/2,y(i)+q1/2,vy(i)+m1/2);

        k3=h*(vx(i)+l2/2);
        l3=h*f(t(i)+h/2,x(i)+k2/2,vx(i)+l2/2,y(i)+q2/2,vy(i)+m2/2);
        q3=h*(vy(i)+m2/2);
        m3=h*g(t(i)+h/2,x(i)+k2/2,vx(i)+l2/2,y(i)+q2/2,vy(i)+m2/2);

        k4=h*(vx(i)+l3);
        l4=h*f(t(i)+h,x(i)+k3,vx(i)+l3,y(i)+q3,vy(i)+m3);
        q4=h*(vy(i)+m3);
        m4=h*g(t(i)+h,x(i)+k3,vx(i)+l3,y(i)+q3,vy(i)+m3);

        x(i+1)=x(i)+(k1+2*k2+2*k3+k4)/6;
        vx(i+1)=vx(i)+(l1+2*l2+2*l3+l4)/6;
        y(i+1)=y(i)+(q1+2*q2+2*q3+q4)/6;
        vy(i+1)=vy(i)+(m1+2*m2+2*m3+m4)/6;        
    end
end

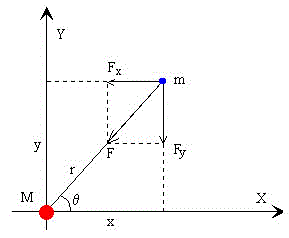
Uno de los ejemplos más interesantes de resolución de un sistema de ecuaciones diferenciales de segundo orden es la descripción del movimiento de los cuerpos celestes, el cual tiene una solución analítica sencilla en coordenadas polares. La trayectoria seguida por un planeta es una cónica, una elipse en particular, en uno de cuyos focos está el centro fijo de fuerzas, el Sol. En la figura, se muestra la fuerza que ejerce el Sol sobre un planeta, inversamente proporcional al cuadrado de las distancias que separan sus centros y también, se muestran sus componentes rectangulares

Teniendo en cuenta que la fuerza que ejerce el Sol sobre un planeta viene descrita por la ley de la Gravitación Universal

$F = G \frac{M m}{r^{2}}$

donde M es la masa del Sol, m la masa del planeta y r la distancia entre el centro del Sol y del planeta. Las componentes de la aceleración del planeta serán

$\begin{array}{l} a_{x} = \frac{- F_{x}}{m} = \frac{- F \cos θ}{m} = - G \frac{M}{r^{3}} x \\ a_{y} = \frac{- F_{y}}{m} = \frac{- F \sin θ}{m} = - G \frac{M}{r^{3}} y \end{array}$

Uno de los problemas del tratamiento numérico con ordenador, es la de reducir el problema a números simples e inteligibles por el usuario de un vistazo. Las masa de los planetas y del Sol son números muy grandes: la masa de la Tierra es 5.98·10²⁴ kg, y 1.98·10³⁰ kg, la del Sol. La distancia media entre la Tierra y el Sol es también muy grande 1.49·10¹¹ m, y la constante G es muy pequeña 6.67·10^-11 en el Sistema Internacional de Unidades.

Escalas

Antes de resolver el sistema de ecuaciones diferenciales por procedimientos numéricos, es conveniente prepararlas para que el ordenador no maneje números excesivamente grandes o pequeños.

Establecemos un sistema de unidades en el que la longitud se mide en unidades astronómicas, la distancia media entre el Sol y la Tierra. L=una UA=1.496·10¹¹ m y el tiempo en unidades de año, P=un año= 365.26 días=3.156·10⁷ s.

En el nuevo sistema de unidades x=Lx’, t=P·t’, la primera ecuación diferencial se escribe

$\begin{array}{l} \frac{d^{2} x^{'}}{d t'^{2}} \frac{L}{P^{2}} = - \frac{G M}{{(x'^{2} + y'^{2})}^{3 / 2}} x' \frac{L}{L^{3}} \\ \frac{d^{2} x^{'}}{d t'^{2}} = - \frac{G M P^{2}}{L^{3}} \frac{x'}{{(x'^{2} + y'^{2})}^{3 / 2}} \end{array}$

Como L es el semieje mayor de la órbita de la Tierra alrededor del Sol, P es el periodo o tiempo que tarda en dar una vuelta completa, y M es la masa del Sol. Por la tercera ley de Kepler, el término

$\frac{G M P^{2}}{L^{3}} = 4 π^{2}$

Volviendo a la notación x e y para la posición y t para el tiempo en el nuevo sistema de unidades. El sistema de ecuaciones diferenciales se escribe

$\begin{array}{l} \frac{d^{2} x}{d t^{2}} = - 4 π^{2} \frac{x}{{(x^{2} + y^{2})}^{3 / 2}} \\ \frac{d^{2} y}{d t^{2}} = - 4 π^{2} \frac{y}{{(x^{2} + y^{2})}^{3 / 2}} \end{array}$

Se resuelve por procedimientos numéricos con las condiciones iniciales siguientes: en el instante t=0, x=x₀, y=0, v_x=0, v_y=v_0y.

Principio de conservación de la energía

La energía total de la partícula es una constante del movimiento. La energía de la partícula de masa m en el instante inicial t=0 es

$E_{0} = \frac{1}{2} m v_{0}^{2} - \frac{G m M}{r_{0}}$

Cuando E₀<0 la partícula permanece confinada en el espacio que rodea a los dos cuerpos. Cuando E₀≥0 la partícula escapa al infinito

La energía de la partícula en el instante t es igual a

$E = \frac{1}{2} m (v_{x}^{2} + v_{y}^{2}) - \frac{G m M}{\sqrt{x^{2} + y^{2}}}$

En el nuevo sistema de unidades establecido

v=v’·L/P, x=x’·L, y=y’·L, d=d’·L

$\begin{array}{l} \frac{E}{m} = \frac{1}{2} v'^{2} \frac{L^{2}}{P^{2}} - \frac{G M_{1}}{L} \frac{1}{\sqrt{x'^{2} + y'^{2}}} \\ \frac{E}{m} = \frac{1}{2} v'^{2} \frac{L^{2}}{P^{2}} - \frac{4 π^{2} L^{2}}{P^{2}} \frac{1}{\sqrt{x'^{2} + y'^{2}}} \\ e^{'} = \frac{E}{m} \frac{P^{2}}{L^{2}} = \frac{1}{2} v'^{2} - 4 π^{2} \frac{1}{\sqrt{x'^{2} + y'^{2}}} \end{array}$

Volviendo a la notación previa. Definimos una nueva energía e por unidad de masa en este sistema de unidades

$e = \frac{1}{2} (v_{x}^{2} + v_{y}^{2}) - 4 π^{2} \frac{1}{\sqrt{x^{2} + y^{2}}}$

El programa evalúa el cociente

$| \frac{e - e_{0}}{e_{0}} | \cdot 100$

que denominaremos tanto por ciento de error. Cuando la energía e difiere apreciablemente de e₀, la trayectoria calculada puede que se desvíe significativamente de la real, y esto suele ocurrir cuando la partícula está muy cerca del centro de fuerzas

Elaboramos un script para describir el movimiento de un cuerpo celeste.

x0=input('posición inicial x: ');
vx0=input('velocidad incial x: ');
y0=0;
vy0=input('velocidad incial y: ');
tf=input('tiempo final, tf: ');
n=input('número de pasos, n: ');

f=@(t,x,vx,y,vy) -4*pi*pi*x/(sqrt(x*x+y*y))^3; 
g=@(t,x,vx,y,vy) -4*pi*pi*y/(sqrt(x*x+y*y))^3;
%condiciones iniciales
t0=0; 
e0=(vx0*vx0+vy0*vy0)/2-4*pi*pi/sqrt(x0*x0+y0*y0); %energía inicial

[t,x,vx,y,vy]=rk_2_2(f,g,t0,tf,x0,vx0,y0,vy0,n);
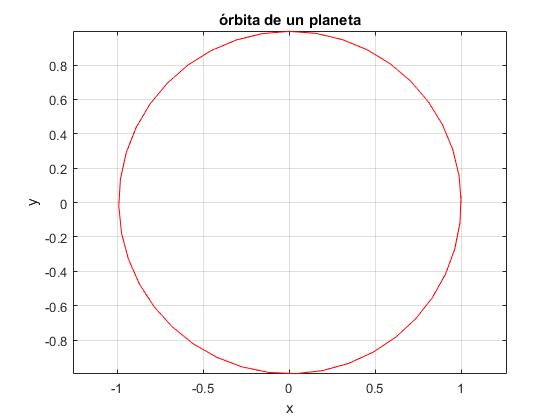
plot(x,y,'r')
xlabel('x')
ylabel('y');
grid on
axis equal
title('órbita de un planeta')
%energía final
ef=(vx(end)*vx(end)+vy(end)*vy(end))/2-4*pi*pi/sqrt(x(end)*x(end)+y(end)*y(end));
%error relativo
fprintf('Error en energía %1.4f\n',abs((ef-e0)/e0))

En la ventana de comandos corremos el script

posición inicial x: 1
velocidad incial x: 0
velocidad incial y: 6.27
tiempo final, tf: 1
número de pasos, n: 40
Error en energía 0.0000