Solución numérica de ecuaciones diferenciales mediante ode45

Su sintaxis es la siguiente

[t,x]=ode45(odefun,tspan,x0, options, params)

x es una matriz donde cada columna corresponde a las variables dependientes y t es el vector tiempo.
odefun es el nombre de la función
tspan especifica el intervalo de tiempo, un vector de dos números tspan=[ti,tf], tiempo inicial y final.
x0 es un vector que contiene los valores iniciales.
options es una estructura que se crea con la función odeset, que explicaremos al final de esta página ya que es un asunto bastante complicado.
params son parámetros que queremos pasar a la función odefun

En la mayor parte de los ejemplos, utilizaremos los tres primeros parámetros: llamaremos al procedimiento ode45 y le pasaremos la función odefunc, los instantes inicial y final en el vector tspan y las condiciones iniciales en el vector x0.

Vamos a volver a resolver los problemas planteados en este capítulo mediante la función MATLAB ode45.

Ecuación diferencial de primer orden

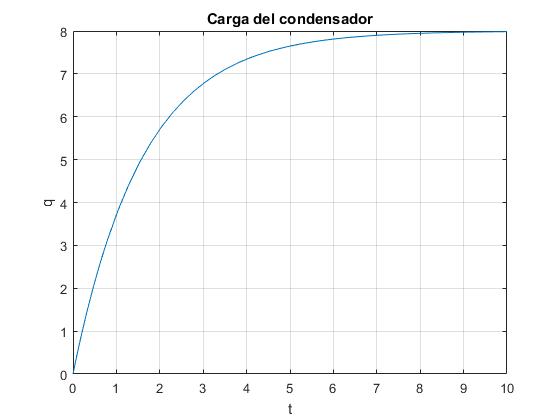
Elaboramos un script para integrar la ecuación diferencial de primer orden que describe la carga de un condensador.

$\frac{d q}{d t} = \frac{V_{ε}}{R} - \frac{q}{R C}$

V0=10;
R=2; %resistencia 
C=0.8; %capacidad ;
tf=10; %tiempo final

f=@(t,x) V0/R-x/(R*C); 
x0=0; %situación inicial
[t,x]=ode45(f,[0,tf],x0); 
plot(t,x)
grid on
xlabel('t')
ylabel('q');
title('Carga del condensador')

Sistema de dos ecuaciones diferenciales de primer orden

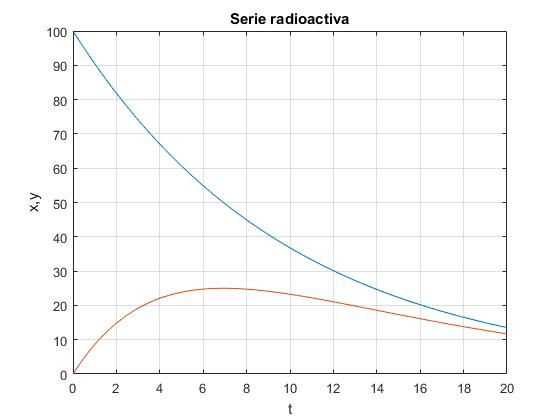
Elaboramos un script para integrar el sistema de dos ecuaciones diferenciales de primer orden que describe la serie de desintagración radioactiva. A-->B-->C donde C es un elemento estable.

${\begin{cases} \frac{d x}{d t} = - a x \\ \frac{d y}{d t} = a x - b y \end{cases}$

En el vector x que devuelve el procedimiento ode45, x(1) representará los sucesivos valores de la variable x y x(2) representará a la variable y. El mismo criterio se empleará para determinar el vector x0 de las condiciones iniciales.

La definición de las funciones f(t,x,y) y g(t,x,y) aparecen en un vector columna, separadas por ; (punto y coma)

fg=@(t,x) [-a*x(1);a*x(1)-b*x(2)]; % x(1) es x, x(2) es y

El script será el siguiente:

a=0.1; %parámetro a
b=0.2; %parámetro b
%condiciones iniciales en el vector x0
x0=[100,0]; %100 es el valor inicial de x, 0 es valor inicial de y
tf=20; %tiempo final, tf

fg=@(t,x) [-a*x(1);a*x(1)-b*x(2)];
[t,x]=ode45(fg,[0,tf],x0);
plot(t,x)
grid on
xlabel('t')
ylabel('x,y');
title('Serie radoioactiva')

En la ventana de comandos corremos el script

Alternativamente, vamos a definir las funciones f(t,x,y) y g(t,x,y) en un fichero .m y le pasamos los valores de los parámetros a y b.

function z=func_radioactivo(t,x,a,b)
    z=[-a*x(1);a*x(1)-b*x(2)]; % x(1) es x, x(2) es y
end

Elaboramos un script para establecer los valores de los parámetros a y b, las condiciones iniciales y llamar a la función que realiza la integración numérica ode45. El primer parámetro de ode45 es el handler (manejador de la función) a integrar que se especifica del siguiente modo @nombre_funcion.

[t,x]=ode45(@func_radioactivo,tspan,x0);

Ahora bien, func_radioactivo precisa de los valores de los parámetros a y b. Hay dos formas de hacerlo. La más sencilla es definir una función anónima fg en términos de func_radioactivo.

fg=@(t,x) func_radioactivo_1(t,x,a,b);

a=0.1; %parámetro a
b=0.2; %parámetro b
%condiciones iniciales en el vector x0
x0=[100,0]; %100 es el valor inicial de x, 0 es valor inicial de y
tf=20; %tiempo final, tf

fg=@(t,x) func_radioactivo(t,x,a,b);
%fg=@(t,x) [-a*x(1);a*x(1)-b*x(2)];
[t,x]=ode45(fg,[0,tf],x0);
plot(t,x)
grid on
xlabel('t')
ylabel('x,y');
title('Serie radioactiva')

Ecuación diferencial de segundo orden

Una vez que se ha entendido como resolver un sistema de dos ecuaciones diferenciales de primer orden es posible entender la resolución de cualquier ecuación diferencial o sistema. Podemos definir las funciones de forma anónima o explícitamente en un fichero .m

$\frac{d x}{d t} = v$

$\frac{d v}{d t} = f (t, x, v)$

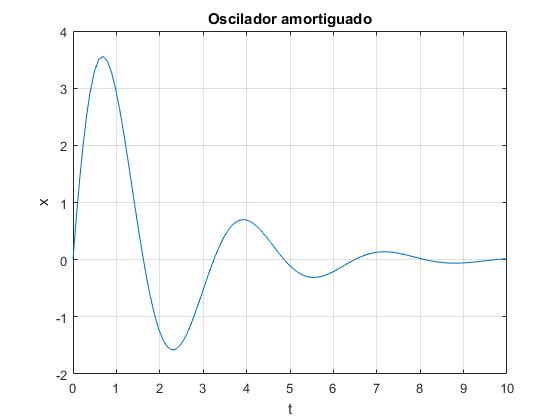
En este sistema de dos ecuaciones diferenciales de primer orden x(1) representará los sucesivos valores de la variable x y x(2) representará a la variable v. El mismo criterio se empleará para determinar el vector x0 de las condiciones iniciales.

Como ejemplo, estudiamos las oscilaciones amortiguadas, que hemos descrito en la página anterior.

$\frac{d^{2} x}{d t^{2}} + 2 γ \frac{d x}{d t} + ω_{0}^{2} x = 0 {\begin{cases} \frac{d x}{d t} = v \\ \frac{d v}{d t} = - 2 γ v - ω_{0}^{2} x \end{cases}$

Las funciones a integrar v, y f (t,x,v) aparecen en un vector columna, separadas por ; (punto y coma)

f=@(t,x) [x(2);-2*g*x(2)-w0*w0*x(1)]; % x(1) es x, x(2) es v

Elaboramos un script para resolver la ecuación de segundo grado que describe las oscilaciones amortiguadas

w0=2; %frecuencia angular
g=0.5; %constante rozamiento
%condiciones iniciales
x0=[0,10]; % 0 es posición inicial, 10 es velocidad inicial
tf=10; %tiempo final

f=@(t,x) [x(2);-2*g*x(2)-w0*w0*x(1)]; 
[t,x]=ode45(f,[0,tf],x0);
plot(t,x(:,1))
grid on
xlabel('t')
ylabel('x');
title('Oscilador amortiguado')

Si solamente queremos representar la posición x(1) en función del tiempo t, se escribe plot(t,x(:,1)). Véase la página Vectores y matrices

Podría ocurrir casos en los que se precisase definir la función f(x,t) en un fichero que denominaremos amortiguadas

function dr=amortiguadas(t, x, g, w0)
    dr=zeros(2,1);
    dr(1)=x(2);
    dr(2)=-2*g*x(2)-w0*w0*x(1);
end

A esta función se le necesita pasar además del vector x, los parámetros g y w0. La llamada a esta función desde el procedimiento ode45 es

w0=2; %frecuencia angular
g=0.5; %constante rozamiento
%condiciones iniciales
x0=[0,10]; % 0 es posición inicial, 10 es velocidad inicial
tf=10; %tiempo final

f=@(t,x) amortiguadas(t,x,g,w0); 
[t,x]=ode45(f,[0,tf],x0);
plot(t,x(:,1))
grid on
xlabel('t')
ylabel('x');
title('Oscilador amortiguado')

Sistema de dos ecuaciones diferenciales de segundo orden

En este caso tenemos un sistema de cuatro ecuaciones difrenciales de primer orden

$\frac{d x}{d t} = v_{x}$	$\frac{d v_{x}}{d t} = f (t, x, v_{x}, y, v_{y})$
$\frac{d y}{d t} = v_{y}$	$\frac{d v_{y}}{d t} = g (t, x, v_{x}, y, v_{y})$

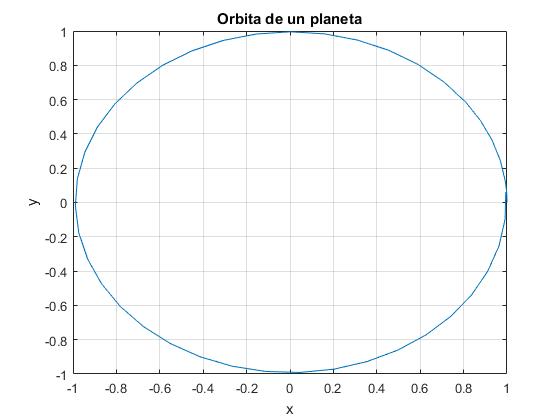
En este sistema x(1) representará los sucesivos valores de la variable x y x(2) representará a la variable v_x, x(3) a la variable y y x(4) a la variable v_y. El mismo criterio se empleará para determinar el vector x0 de las condiciones iniciales.

Como ejemplo, estudiamos el movimiento de un planeta alrededor del Sol o de un satélite artificial alrededor de la Tierra.

$\begin{array}{l} \frac{d^{2} x}{d t^{2}} = - 4 π^{2} \frac{x}{{(x^{2} + y^{2})}^{3 / 2}} {\begin{cases} \frac{d x}{d t} = v_{x} \\ \frac{d v_{x}}{d t} = - 4 π^{2} \frac{x}{{(x^{2} + y^{2})}^{3 / 2}} \end{cases} \\ \frac{d^{2} y}{d t^{2}} = - 4 π^{2} \frac{y}{{(x^{2} + y^{2})}^{3 / 2}} {\begin{cases} \frac{d y}{d t} = v_{y} \\ \frac{d v_{y}}{d t} = - 4 π^{2} \frac{y}{{(x^{2} + y^{2})}^{3 / 2}} \end{cases} \end{array}$

Elaboramos un script para resolver el sistema de dos ecuaciones de segundo grado que describe el movimiento de un cuerpo celeste.

%posición inicial x, velocidad x, posición y, velocidad y
x0=[1,0,0,6.27];
tf=1; %tiempo final

fg=@(t,x)[x(2);-4*pi*pi*x(1)/(sqrt(x(1)*x(1)+x(3)*x(3)))^3; x(4);
-4*pi*pi*x(3)/(sqrt(x(1)*x(1)+x(3)*x(3)))^3];
[t,x]=ode45(fg,[0,tf],x0);
plot(x(:,1),x(:,3))
grid on
xlabel('x')
ylabel('y');
title('Orbita de un planeta')

Representamos la trayectoria, es decir, los puntos de abscisas x(:,1) que guardan los valores x y las ordenadas x(:,3) que guardan los valores y, en función del tiempo t, se escribe plot(x(:,1),x(:,3)).

Podría ocurrir casos en los que se precisase definr la función f(x,t) en un fichero que denominaremos planeta

function dr=planeta(t, x)
    dr=zeros(4,1);
    dr(1)=x(2);
    dr(2)=-4*pi*pi*x(1)/(sqrt(x(1)*x(1)+x(3)*x(3)))^3;
    dr(3)=x(4);
    dr(4)=-4*pi*pi*x(3)/(sqrt(x(1)*x(1)+x(3)*x(3)))^3;
end

La llamada a esta función desde el procedimiento ode45 es

%posición inicial x, velocidad x, posición y, velocidad y
x0=[1,0,0,6.27];
tf=1; %tiempo final

[t,x]=ode45(@planeta,[0,tf],x0);
plot(x(:,1),x(:,3))
grid on
xlabel('x')
ylabel('y');
title('Orbita de un planeta'

Opciones de ode45

Imaginemos que estudiamos el movimiento de caída de un cuerpo, no sabemos cuanto tiempo tardará en llegar al suelo, desconocemos el valor del elemento tf en el vector tspan. Sin embargo, queremos detener el proceso de integración numérica de la ecuación diferencial que describe el movimiento cuando la posición del móvil sea cero. La función MATLAB ode45 dispone de un parámetro adicional options donde podemos indicarlo.

Detener la integración de la ecuación diferencial

La opción más importante cuando resolvemos ecuaciones diferenciales es la de detener la integración numérica cuando se cumple una o varias condiciones

En el ejemplo, del movimiento de un cuerpo celeste, queremos que la integración del sistema de dos ecuaciones diferenciales se detenga cuando regrese a la posición inicial.

Los pasos a seguir son los siguientes:

El cuerpo celeste parte de la posición (1,0). Definimos la función cuyo nombre es stop_planeta y que detiene la integración cuando la ordenada y vuelve a ser es cero.

function [value,isterminal,direction]=stop_planeta(t,x)
   %x(1) es  x, x(3) es y
    value=x(3);
    isterminal=1; %1 detiene la integración cuando la velocidad se hace cero   
    direction=1; % 1 crece, -1 decrece, 0 no importa
end

Creamos la estructura opts con la llamada a la función odeset

opts=odeset('events',@stop_planeta);

Cuando se utiliza options el procedimiento ode45 devuelve los tiempos te en los cuales ocurren los 'eventos' y los correspondientes valores de las variables dependientes (posición, velocidad) en el vector xe. Finalmente, ie es un índice que es útil cuando se vigilan varios eventos.

Le pasamos opts al procedimiento ode45 en su cuarto parámetro

[t,x,te,xe,ie]=ode45(odefunc,tspan,x0,opts);

Creamos un script para resolver la ecuación diferencial de segundo orden y detener el proceso de integración de acuerdo con lo estipulado en el parámetro opts.

%posición inicial x, velocidad x, posición y, velocidad y
x0=[1,0,0,6.27];
tf=10; %tiempo final

opts=odeset('events',@stop_planeta);
fg=@(t,x)[x(2);-4*pi*pi*x(1)/(sqrt(x(1)*x(1)+x(3)*x(3)))^3; x(4);
-4*pi*pi*x(3)/(sqrt(x(1)*x(1)+x(3)*x(3)))^3];
[t,x, te]=ode45(fg,[0,tf],x0,opts);
plot(x(:,1),x(:,3))
grid on
xlabel('x')
ylabel('y');
title('Orbita de un planeta')

En la ventana de comandos vemos el tiempo te que tarda el cuerpo celeste en completar una vuelta

te =
    0.0000
    0.9779

En la página web titulada Una esfera que choca con un escalón cuya altura es menor que su radio. Si la velocidad inicial de la esfera es mayor que un valor crítico, la esfera apoyada en la esquina del escalón gira 90 grados y continúa su movimiento con una velocidad menor. Si es menor que el valor crítico, la esfera gira hasta un ángulo máximo cuando su velocidad angular se hace cero y regresa al punto de partida con la misma velocidad pero de sentido contrario

Resolvemos la ecuación diferencial con las condiciones iniciales: en el instante t=0, la posición angular θ=θ₀, la velocidad angular dθ/dt=(dθ/dt)₀ (w0 en el código)

$\frac{d^{2} θ}{d t^{2}} = - \frac{5}{7} \frac{g}{R} \cos θ$

h=0.3;  %altura escalón
R=1; %radio esfera
v0=2; %velocidad incial
w0=(1-5*h/(7*R))*v0/R; %velocidad angular inicial
th_0=asin((R-h)/R); %ángulo inicial
x0=[th_0,w0];
f=@(t,x) [x(2); -5*9.8*cos(x(1))/(7*R)]; 
opts=odeset('events',@stop_esfera_escalon);
[t,x, te, xe,ie]=ode45(f,[0,50],x0,opts);
plot(t, x(:,1))
grid on
xlabel('t')
ylabel('\theta')
title('Esfera que choca con un escalón')

Definimos la función stop_esfera_escalon, para que el movimiento de la esfera se detenga

Cuando su posición angular alcance, θ=π/2 ( 90°)
Cuando alcance el ángulo máximo, θ_m con velocidad angular cero

function [value,isterminal,direction]=stop_esfera_escalon(t,x)
    value=[x(2), x(1)-pi/2];  
    isterminal=[1, 1];
    direction=[-1,1]; 
end

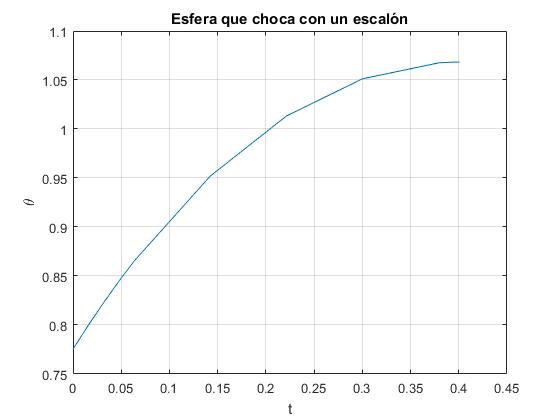
La variable xe nos proporciona la posición angular y la velocidad angular final, y la variable te el tiempo. Cuando la velocidad inicial v₀=2, el centro de la esfera gira un ángulo máximo θ_m=1.07 (61.2°), hasta que se detiene, empleando un tiempo de 0.4.

>> te
te =    0.4007
>> xe
xe =    1.0682   -0.0000

Cuando cambiamos la velocidad inicial a v₀=3, la posición angular final es π/2 (90°), y la velocidad angular final 1.16. El centro de la esfera gira 90° y proseguirá su movimiento en el escalón a una velocidad menor

>> te
te =    0.5139
>> xe
xe =    1.5708    1.1643

Para el caso de la velocidad inicial v₀=2, nos podría interesar el movimiento completo de la esfera, girando alrededor de la esquina del escalón. La esfera parte de la posición incial θ₀ en el instante t=0, alcanza la máxima posición angular θ_m=1.07 (61.2°), con velocidad angular nula y retorna a la posición inicial θ₀ con la misma velocidad que la de partida pero en sentido contrario. Redefinimos la función stop_esfera_escalon

function [value,isterminal,direction]=stop_esfera_escalon(t,x, th_0)
    value=[x(1)-th_0, x(1)-pi/2];  
    isterminal=[1, 1];
    direction=[-1,1]; 
end

Este ejemplo, ilustra además, la forma de pasar parámetros a la función stop_esfera_escalon, que nos puede ser muy últil en la resolución de ecuaciones diferenciales

h=0.3;  %altura escalón
R=1; %radio esfera
v0=2; %velocidad incial
w0=(1-5*h/(7*R))*v0/R; %velocidad angular inicial
th_0=asin((R-h)/R); %ángulo inicial
x0=[th_0,w0];
f=@(t,x) [x(2); -5*9.8*cos(x(1))/(7*R)]; 
opts=odeset('events',@(t,x) stop_esfera_escalon(t,x,th_0));
[t,x, te, xe,ie]=ode45(f,[0,50],x0,opts);
plot(t, x(:,1))
grid on
xlabel('t')
ylabel('\theta')
title('Esfera que choca con un escalón')

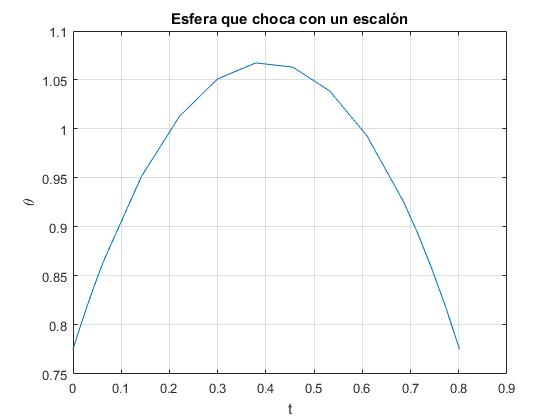
Vuelve a la posición inicial, con la misma velocidad angular de partida (cambiada de signo) después de un tiempo t=0.8

>> te
te =    0.8015
>> xe
xe =    0.7754   -1.5712
>> w0
w0 =    1.5714
>> th_0
th_0 =    0.7754

Resaltar información relevante

A veces nos interesa además, resaltar información relevente en las gráficas, máximos, mínimos, puntos de corte con el eje X, etc.

Volvamos a considerar el oscilador amortiguado estudiado anteriormente, de frecuencia natural ω₀=2, constante de amortiguamiento γ=0.25, parte de la posición x₀=2.5 con velocidad nula. Queremos detener el proceso de integración cuando el móvil alcance la posición máxima, cuando su velocidad es nula, tal como se muestra en la figura (más abajo), con lo que se completa un periodo.

Volvemos a describir los pasos a seguir:

Definimos la función cuyo nombre es opcion_ode45

function [value,isterminal,direction]=opcion_ode45(t,x)
    value=[x(1) x(2)]; %[posición, velocidad]
    %1 indice que detiene la integración cuando la velocidad se hace cero   
    isterminal=[0 1];
    direction=[0 -1]; % 1 crece, -1 decrece, 0 no importa
end

Creamos la estructura opts con la llamada a la función odeset

opts=odeset('events',@opcion_ode45);

Cuando se utiliza options la función ode45 devuelve los tiempos te en los cuales ocurren los 'eventos' y los correspondientes valores de las variables dependientes (posición, velocidad) en el vector xe. Finalmente, ie es un índice que es útil cuando se vigilan varios eventos.

Le pasamos opts al procedimiento ode45 en su cuarto parámetro

[t,x,te,xe,ie]=ode45(odefunc,tspan,x0,opts);

Escribimos un script para resolver la ecuación diferencial de segundo orden y detener el proceso de integración de acuerdo con lo estipulado en el parámetro opts.

w0=2;
g=0.25;
x0=[2.5 0]; %posición inicial, velocidad inicial
tf=10;
f=@(t,x) [x(2);-2*g*x(2)-w0*w0*x(1)]; 
tf=10;

opts=odeset('events',@opcion_ode45);
[t,x,te,xe,ie]=ode45(f,[0,tf],x0,opts);
plot(t,x(:,1))
grid on
xlabel('t')
ylabel('x');
title('Oscilador amortiguado')

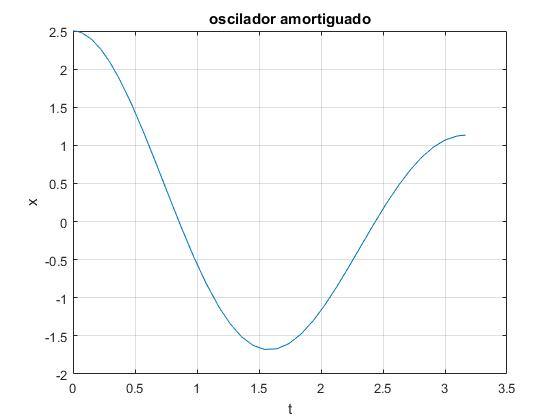
En la ventana de comandos se imprime los siguientes datos relativos a los eventos, que se explican en la tabla.

>> te,xe,ie
te =
    0.0000
    0.8547
    2.4378
    3.1662
xe =
    2.5000   -0.0000
   -0.0000   -4.0378
    0.0000    2.7173
    1.1322   -0.0000
ie =
     2
     1
     1
     2

Tiempo, te	Posición x(1)	Velocidad x(2)	Indice ie
0.0000	2.5000	-0.0000	2
0.8547	-0.0000	-4.0378	1
2.4378	0.0000	2.7173	1
3.1662	1.1322	-0.0000	2

Cuando parte de la posición inicial x(1)=2.5 la velocidad es cero x(2)=0, detecta velocidad (índice ie=2).
Cuando pasa por el origen x(1)=0 detecta posición (índice ie=1), pero no se detiene ya que en isterminal se ha puesto un cero.
Cuando la posición es x(1)=1.1322 detecta velocidad nula x(2)=0, (índice ie=2) y la integración numérica se detiene ya que en isterminal se ha puesto un uno y la velocidad decrece en direction se ha puesto un -1.

La columna de tiempos nos porporciona el periodo de la oscilación, te=3.1662.

Se sugiere al lector, cambiar en la función opcion_ode45

direction=[0 1];

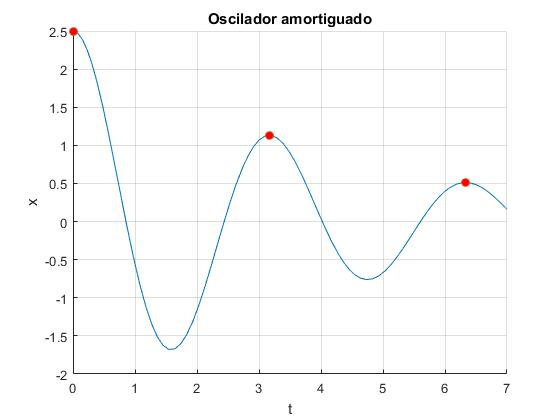
Vamos ahora a marcar en la representación gráfica de la oscilación amortiguada, las posiciones de máxima amplitud x(2)=0 y cuando pasa por el origen x(1)=0 sin detener la integración numérica.

Definimos una nueva versión de la función opcion1_ode45

function [value,isterminal,direction]=opcion1_ode45(t,x)
    value=[x(1), x(2)]; %[posición, velocidad]
   isterminal=[0, 0];
    direction=[0, 0]; 
end

Creamos la estructura opts mediante odeset y se la pasamos al procedimiento ode45.

w0=2;
g=0.25;
x0=[2.5 0]; %posición inicial, velocidad inicial
tf=10;
f=@(t,x) [x(2);-2*g*x(2)-w0*w0*x(1)]; 
tf=7;
opts=odeset('events',@opcion1_ode45);
[t,x,te,xe,ie]=ode45(f,[0,tf],x0,opts);
hold on
plot(t,x(:,1))
plot(te(ie==1),xe(ie==1),'o','markersize',6,'markerfacecolor','r')
plot(te(ie==2),xe(ie==2),'o','markersize',6,'markerfacecolor','b')
hold off
grid on
xlabel('t')
ylabel('x');
title('Oscilador amortiguado')

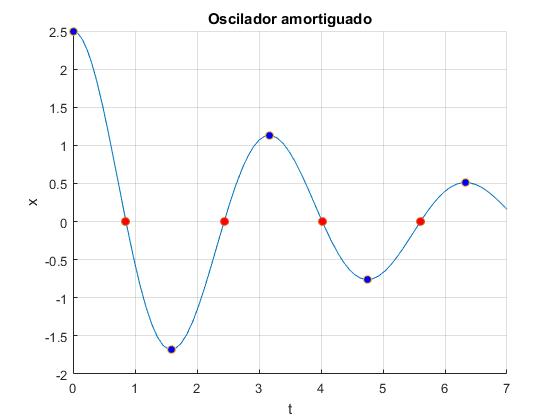
Si solamente estamos interesados en los máximos definimos una nueva versión de la función opcion1_ode45

function [value,isterminal,direction]=opcion1_ode45(t,x)
    value=x(2); %[posición, velocidad]
   isterminal=0;
    direction=-1; 
end

Modificamos el script

w0=2;
g=0.25;
x0=[2.5 0]; %posición inicial, velocidad inicial
tf=10;
f=@(t,x) [x(2);-2*g*x(2)-w0*w0*x(1)]; 
tf=7;
opts=odeset('events',@opcion1_ode45);
[t,x,te,xe,ie]=ode45(f,[0,tf],x0,opts);
hold on
plot(t,x(:,1))
plot(te(ie==1),xe(ie==1),'o','markersize',6,'markerfacecolor','r')
hold off
grid on
xlabel('t')
ylabel('x');
title('Oscilador amortiguado')

El paso de integración

En el procedimiento Runge-Kutta de integración de ecuaciones diferenciales requiere un paso que se especifica en la variable h. El procedimiento ode45 de MATLAB no lo requiere. Pero vamos a ver mediante un ejemplo que a veces es necesario

Resolvemos el sistema de ecuaciones diferenciales que describe el movimiento de una partícula sobre una plataforma en rotación

${\begin{cases} \frac{d^{2} ξ}{d τ^{2}} - ξ {(\frac{d θ}{d τ})}^{2} = ξ - \frac{1}{\sqrt{{(\frac{d ξ}{d τ})}^{2} + ξ^{2} {(\frac{d θ}{d t})}^{2}}} \frac{d ξ}{d τ} + 2 ξ \frac{d θ}{d τ} \\ ξ \frac{d^{2} θ}{d τ^{2}} + 2 \frac{d ξ}{d τ} \frac{d θ}{d τ} = - \frac{1}{\sqrt{{(\frac{d ξ}{d τ})}^{2} + ξ^{2} {(\frac{d θ}{d τ})}^{2}}} ξ \frac{d θ}{d τ} - 2 \frac{d ξ}{d τ} \end{cases}$

La partícula parte del origen ξ=0, θ=0, con velocidad radial dξ/dτ=2, dθ/dt=0. Representamos la trayectoria hasta el instante τ=80

% x(1) es r, x(2) dr/dt, x(3) es th, x(4) dth/dt
fg=@(t,x)[x(2); x(1)*x(4)^2+x(1)+2*x(1)*x(4)-x(2)/sqrt(x(2)^2+x(1)^2*x(4)^2); 
x(4); -2*x(2)*x(4)/x(1)-2*x(2)/x(1)-x(4)/sqrt(x(2)^2+x(1)^2*x(4)^2)];
[~,x]=ode45(fg,[0,80],[eps, 2, 0, 0]); %eps evita la división entre cero
xx=x(:,1).*cos(x(:,3));
yy=x(:,1).*sin(x(:,3));
plot(xx,yy)
axis equal
grid on
xlabel('x')
ylabel('y');
title('Partícula sobre un disco en rotación')

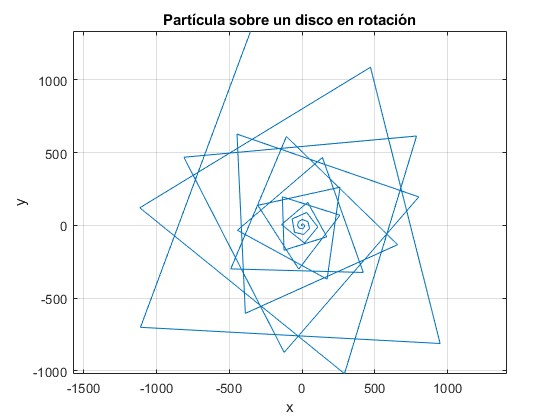
La representación gráfica de la trayectoria de la partícula es completamente insatisfactoria

Si cambiamos el vector de los instantes inicial y final [0,80] por un vector de tiempos, linspace(0,80,300) la representación gráfica mejora sustancialmente

% x(1) es r, x(2) dr/dt, x(3) es th, x(4) dth/dt
fg=@(t,x)[x(2); x(1)*x(4)^2+x(1)+2*x(1)*x(4)-x(2)/sqrt(x(2)^2+x(1)^2*x(4)^2); 
x(4); -2*x(2)*x(4)/x(1)-2*x(2)/x(1)-x(4)/sqrt(x(2)^2+x(1)^2*x(4)^2)];
[~,x]=ode45(fg,linspace(0,80,300),[eps, 2, 0, 0]);
xx=x(:,1).*cos(x(:,3));
yy=x(:,1).*sin(x(:,3));
plot(xx,yy)
axis equal
grid on
xlabel('x')
ylabel('y');
title('Partícula sobre un disco en rotación')

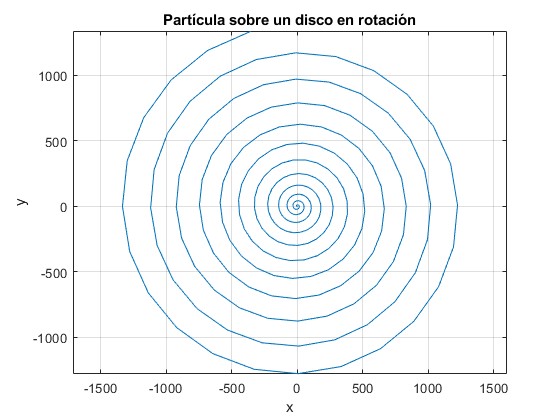
Paso de parámetros a la función

Como hemos visto, a ode45 se le pasa la función (handle) a integrar en su primer argumento. Si la función contiene parámetros como la frecuencia angular ω₀, no hay problema si la función se define como anónima, tal como se ha mostrado en los ejemplos previos. Si la función se define en un fichero entonces a la función se le pasan los valores de los parámetros en el quinto argumento params de ode45. Los pasos se explican en el siguiente ejemplo:

El sistema de ecuaciones de Lorentz es un sistema de tres ecuaciones diferenciales de primer orden

$\begin{array}{l} \frac{d x}{d t} = - σ x + σ y \\ \frac{d y}{d t} = ρ x - y - x z \\ \frac{d z}{d t} = - β z + x y \end{array}$

donde σ=10, β=8/3 y ρ=28

Vamos a resolver el sistema de tres ecuaciones diferenciales con las condiciones iniciales siguientes: en el instante t=0, x₀=-8, y₀=8 z₀=27.

Escribir una función denominada lorentz(t,x,p) como fichero .m que contenga las tres ecuaciones y dependa de los tres parámetros σ=p(1), β=p(2) y ρ=p(3). Observar que la variable x se guarda en el primer elemento x(1), la variable y en el segundo x(2) y la variable z en el tercer x(3) elemento del vector x.
Escribir un script denominado que llame a la función MATLAB ode45, para resolver el sistema de ecuaciones diferenciales para las condiciones iniciales especificadas.
Pasar los parámetros σ, β y ρ como elementos de un vector p al procedimiento ode45 para que a su vez se los pase a la función lorentz.
Representar z en función de x hasta el instante t_f=20 en una primera ventana gráfica.
Dibujar x, y y z en función del tiempo en tres zonas de una segunda ventana gráfica.
Examinar el comportamiento del sistema para otras condiciones iniciales, t=0, x₀=1, y₀=2 z₀=3.

Definimos la función lorentz como fichero .m

function fg=lorentz(t,x,p)    
%x(1) es x, x(2) es y y x(3) es z
% p(1) es sigma, p(2) es beta y p(3) es rho
    fg=[-p(1)*x(1)+p(1)*x(2); p(3)*x(1)-x(2)-x(1)*x(3); -p(2)*x(3)+x(1)*x(2)]; 
end

Elaboramos el script

x0=[-8 8 27]; %valores iniciales
tf=20; %instante final
p=[10 8/3 28]; %parámetros
%no pasamos nada [] en el parámetro options de ode45
[t,x]=ode45(@lorentz,[0,tf],x0,[],p);
figure
plot(x(:,1),x(:,3),'r')
xlabel('x')
ylabel('z');
title('Atractor de Lorentz')

figure
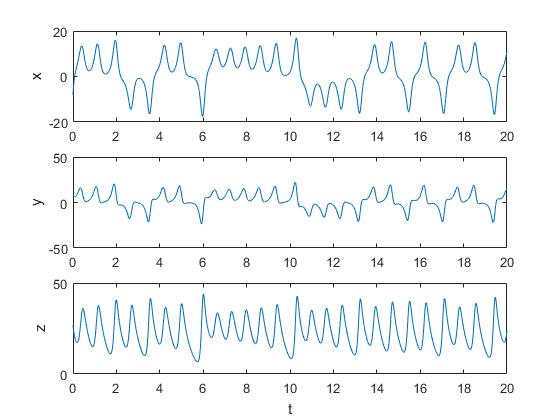
subplot(3,1,1)
plot(t,x(:,1))
ylabel('x');
subplot(3,1,2)
plot(t,x(:,2))
ylabel('y');
subplot(3,1,3)
plot(t,x(:,3))
ylabel('z');
xlabel('t')

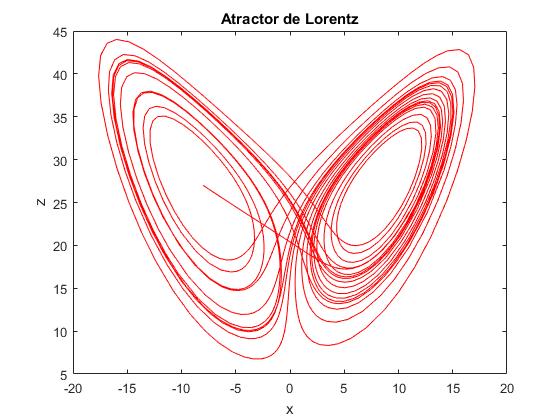
Aparecen dos ventanas gráficas, la primera con el atractor de Lorentz, la representación z(x) y la segunda ventana dividida en tres regiones que muestran x(t), y(t) y z(t)

Otra forma de pasar parámetros

Se pasan los parámetros a la función a integrar de la siguiente forma

x0=[-8,8,27]; %valores iniciales
tf=20; %instante final
sigma=10;
beta=8/3;
rho=28;
fg=@(t,x) lorentz_1(t,x,sigma, beta, rho); 
[t,x]=ode45(fg,[0,tf],x0);
figure
plot(x(:,1),x(:,3),'r')
xlabel('x')
ylabel('z');
title('Atractor de Lorentz')
figure
subplot(3,1,1)
plot(t,x(:,1))
ylabel('x');
subplot(3,1,2)
plot(t,x(:,2))
ylabel('y');
subplot(3,1,3)
plot(t,x(:,3))
ylabel('z');
xlabel('t')

La definición de la función denominada lorentz_1, guardada en un fichero es

function z=lorentz_1(t,x,sigma, beta, rho)    
%x(1) es x, x(2) es y y x(3) es z
    z=[-sigma*x(1)+sigma*x(2); rho*x(1)-x(2)-x(1)*x(3); -beta*x(3)+x(1)*x(2)]; 
end

Este modo de pasar parámetros a la función a integrar es preferible y más transparente que la forma anterior

Ejemplos en el curso de Física