Procedimiento bvp4c de MATLAB

El procedimiento sol = bvp4c(odefun,bcfun,solinit), integra un sistema de cuaciones diferenciales de la forma

${\displaystyle \frac{dy}{dx}=f(x,y)}$

en el intervalo [a,b], bajo las condiciones de contorno especificadas por una función g(y(a),y(b))=0. ya e yb son vectores de dos componentes ya(1), ya(2); yb(1), yb(2)

${\displaystyle ya=\left[\begin{array}{l}y(a)\\ {\frac{dy}{dx}|}_{x=a}\end{array}\right],yb=\left[\begin{array}{l}y(b)\\ {\frac{dy}{dx}|}_{x=b}\end{array}\right]}$

Se define la función bcfun que devuelve,

${\displaystyle \left[\begin{array}{l}ya(1)-\alpha \\ ya(2)-\beta \end{array}\right]}$

para una función y(x) definida en el intervalo [a,b] cuyos extremos tienen valores fijos α y β. Pero también podrían estar fijados los valores de las pendientes de la función en dichos puntos

${\displaystyle \left[\begin{array}{l}ya(2)-{\frac{dy}{dx}|}_{x=a}\\ yb(2)-{\frac{dy}{dx}|}_{x=b}\end{array}\right]}$

o una combinación de ambas, hay otras posibilidades de condiciones de contorno

${\displaystyle \left[\begin{array}{l}ya(1)-\alpha \\ yb(2)-{\frac{dy}{dx}|}_{x=b}\end{array}\right]}$

Se utiliza bvpinit para crear la aproximación inicial de la solución de la ecuación diferencial

solinit = bvpinit(linspace(a,b,5), [s1,s2]);

Al primer argumento, se le pasa un vector de puntos iniciales en el intervalo [a,b], son suficientes cinco valores igualmente espaciados, linspace(a,b,5)

Al segundo, se le pasa un vector de dos componentes [s1,s2] que se refieren a la aproximación inicial de y y de dy/dx. Habitualmente, son valores fijos. Pero también podría venir de una función que pensamos que se aproxima a la solución buscada. En un movimiento periódico, podrían ser funciones trigonométricas, seno y coseno

...
xIni=linspace(a,b,5);
solinit = bvpinit(xIni, @guess); 

function g = guess(x)   
    g = [sin(x), cos(x)];
end 

Se utiliza la función deval y el valor sol devuelto del procedimiento bvp4c para evaluar y representar la solución para valores x del intervalo [a,b]

El procedimiento bvp4c admite parámetros y opciones adicionales. En esta página, solamente describiremos su funcionamiento más básico.

Ejemplos

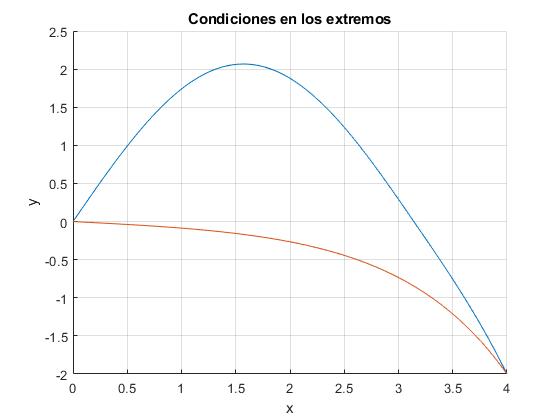
Vamos a integrar la ecuación diferencial con las condiciones en los extremos a=0, b=4

${\displaystyle \frac{d^{2}y}{d{x}^2}+\left|y\right|=\mathrm{0,}\{\begin{array}{l}y(0)=0\\ y(4)=-2\end{array}}$

El procedimiento sol = bvp4c(odefun,bcfun,solinit) nos pide los valores de tres parámetros:

1. Como hemos visto al aplicar el procedimientro ode45, una ecuación diferencial de segundo orden se convierte en un sistema de dos ecuaciones diferenciales de primer orden

function dx = odefun(~,x)
    dx = [x(2), -abs(x(1))];
end

2. Definimos la función que especifica las condiciones en los extremos

function res = bcfun(xa,xb)
    res = [xa(1), xb(1)+2];
end

3. Definimos la aproximación inicial en solinit, que va a consistir en cinco puntos 0,1,2,3,4,5 en el intervalo [0,4] y una aproximación inicial [s1, s2]. La elección adecuada de la aproximación inicial es crucial para econtrar la solución. En los ejemplos que siguen eligiremos valores constantes, pero no siempre es posible para encontrar la solución buscada

solinit = bvpinit(linspace(0,4,5), [1,0]);

Se los pasamos al procedimiento bvp4c

sol = bvp4c(@odefun, @bcfun, solinit);

Con el valor devuelto sol, y utilizando la función deval, representamos la solución y(x) en el intervalo [a,b]

...
x=linspace(0,4); %100 puntos, por defecto
y = deval(sol,x);
plot(x,y(1,:));
...

La ecuación diferencial admite dos soluciones, la segunda se obtiene con la aproximación inicial

solinit = bvpinit(linspace(0,4,5), [-1,0]);

Reunimos las porciones de código, para crear la función ecuacion_diferencial_1 que contiene todo el código, incluidas las subfunciones

function ecuacion_diferencial_1
    solinit = bvpinit(linspace(0,4,5), [1,0]); %primera aproximación
    sol1 = bvp4c(@odefun, @bcfun, solinit); 
    solinit = bvpinit(linspace(0,4,5), [-1,0]); %segunda aproximación
    sol2 = bvp4c(@odefun, @bcfun, solinit); 
    x=linspace(0,4);
    y = deval(sol1,x);
    hold on
    plot(x,y(1,:));
    y = deval(sol2,x);
    plot(x,y(1,:));
    grid on
    xlabel('x')
    ylabel('y')
    title('Condiciones en los extremos')
    
%ecuación diferencial
    function dx = odefun(~,x)
        dx = [x(2), -abs(x(1))];
    end
%condiciones en los extremos
    function res = bcfun(xa,xb)
        res = [xa(1), xb(1)+2];
    end
end

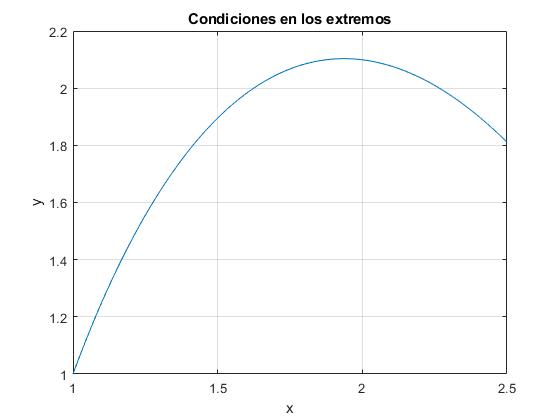
Sea la ecuación diferencial, con las condiciones en los extremos a=1, b=2.5

${\displaystyle x\frac{d^{2}y}{d{x}^2}+\frac{dy}{dx}+2x=\mathrm{0,}\{\begin{array}{l}y(1)=1\\ {\frac{dy}{dx}|}_{x=2.5}=-1\end{array}}$

function ecuacion_diferencial_8
    solinit = bvpinit(linspace(1,2.5,5), [0.1,0]);
    sol = bvp4c(@f, @extremos, solinit);
    t=linspace(1,2.5);
    x = deval(sol,t);
    plot(t,x(1,:));
    grid on
    xlabel('x')
    ylabel('y')
    title('Condiciones en los extremos')
    disp(x(2,end)) %pendiente en x=2.5

%ecuación diferencial
    function dx = f(t,x)
        dx = [x(2), -x(2)/t-2];
    end
%condiciones en los extremos
    function res = extremos(xa,xb)
        res = [xa(1)-1, xb(2)+1];
    end
end

Comprobamos con x(2,end) que la pendiente de la función y(x) en x=2.5 es -1

>> ecuacion_diferencial_8
    -1

A final de la la página titulada Cuerda que gira alrededor de un eje, se describe un ejemplo significativo, comparándose la solución analítica y la que resulta de la aplicación del procedimiento bvp4c

Aproximaciones sucesivas

Un problema típico de cinemática es el de apuntar un cañón para que el proyectil disparado impacte en el blanco. Tenemos dos posiciones la de disparo y la del blanco. Elegimos un ángulo de tiro, si el alcance es mayor o menor que la distancia desde la posición de disparo al blanco, cambiamos el ángulo de tiro y así, mediante aproximaciones sucesivas obtenemos el ángulo de disparo que hace que el proyectil impacte en el blanco.

El procedimiento para resolver la ecuación diferencial

${\displaystyle \begin{array}{l}\frac{d^{2}y}{d{x}^2}=f\left(x,y,\frac{dy}{dx}\right),a\le x\le b\\ y(a)=\alpha ,y(b)=\beta \end{array}}$

es similar, se trata de elegir el valor adecuado ${\frac{dy}{dx}|}_{x=a}=s$, de la derivada primera en x=a (tangente del ángulo de tiro), para que al resolver la ecuación diferencial en el intervalo [a,b], obtengamos y(b)=β (acertar en el blanco).

Ecuaciones lineales

Supongamos que la ecuación diferencial con las condiciones en los extremos

${\displaystyle \begin{array}{l}\frac{d^{2}y}{d{x}^2}+p(x)\frac{dy}{dx}+q(x)y+r(x)=0\\ y(a)=\alpha ,y(b)=\beta \end{array}}$

La elección de la pendiente inicial, se realiza aplicando el principio de superposición

1. Sean las condiciones iniciales:

${\displaystyle y(a)=\alpha ,{\frac{dy}{dx}|}_{x=a}=s_1}$

resolvemos la ecuación diferencial y obtenemos la solución y₁(x). En el extremo b, y₁(b)=β₁ que será en general, distinto de β

2. Sean las condiciones iniciales:

${\displaystyle y(a)=\alpha ,{\frac{dy}{dx}|}_{x=a}=s_2}$

resolvemos la ecuación diferencial y obtenemos la solución y₂(x). En el extremo b, y₂(b)=β₂ que será en general, distinto de β

La solución de la ecuación diferencial es también la combinación lineal

${\displaystyle y(x)=\frac{c_1{y}_1(x)+c_2{y}_2(x)}{c_1+c_2}}$

como puede verificase fácilmente

${\displaystyle \begin{array}{l}{c}_1\frac{d^2{y}_1}{d{x}^2}+c_2\frac{d^2{y}_2}{d{x}^2}+p(x)\left(c_1\frac{d{y}_1}{dx}+c_2\frac{d{y}_2}{dx}\right)+q(x)\left(c_1{y}_1+c_2{y}_2\right)y+r(x)\left(c_1+c_2\right)=0\\ c_1\left(\frac{d^2{y}_1}{d{x}^2}+p(x)\frac{d{y}_1}{dx}+q(x)y_1+r(x)\right)+c_2\left(\frac{d^2{y}_2}{d{x}^2}+p(x)\frac{d{y}_2}{dx}+q(x)y_2+r(x)\right)=0\end{array}}$

• En x=b se cumple

${\displaystyle \begin{array}{l}y(b)=\frac{c_1{y}_1(b)+c_2{y}_2(b)}{c_1+c_2}\\ \beta =\frac{c_1{\beta }_1+c_2{\beta }_2}{c_1+c_2}\end{array}}$

• En x=a se cumple

${\displaystyle \begin{array}{l}y\text{'}(a)=\frac{c_{1}y{\text{'}}_1(a)+c_{2}y{\text{'}}_2(a)}{c_1+c_2},y\text{'}(x)=\frac{dy}{dx}\\ s=\frac{c_1{s}_2+c_2{s}_2}{c_1+c_2}\end{array}}$

Asignamos a c₂=1. Eliminamos c₁ el sistema de dos ecuaciones

${\displaystyle s=\frac{\beta (s_2-s_1)+s_1{\beta }_2-s_2{\beta }_1}{{\beta }_2-{\beta }_1}}$

Ejemplo

Resolvamos la ecuación diferencial, con las condiciones en los extremos que se especifican

${\displaystyle \begin{array}{l}\frac{d^{2}y}{d{x}^2}-\left(1-\frac{x}{5}\right)y-x=0\\ y(1)=\mathrm{2,}y(3)=-1\end{array}}$

• para ${s_1=\frac{dy}{dx}|}_{x=a}=-1.5$, obtenemos, β₁=4.7876

• para ${s_2=\frac{dy}{dx}|}_{x=a}=-3$, obtenemos, β₂=0.4360

Calculamos s a partir de s₁, s₂, β₁, β₂ y β

para ${s=\frac{dy}{dx}|}_{x=a}=-3.4950$, obtenemos β=-1, al resolver la ecuación diferencial

alfa=2; %en x=1
beta=-1; %en x=3
f=@(t,x) [x(2); (1-t/5)*x(1)+t]; 
s1=-1.5; %pendiente en x=1
[t,x]=ode45(f,[1,3],[alfa,s1]);
beta_1=x(end,1);
hold on
plot(t, x(:,1))

s2=-3.0; %pendiente en x=1
[t,x]=ode45(f,[1,3],[alfa,s2]);
beta_2=x(end,1);
plot(t, x(:,1))

s=(beta*(s1-s2)-s1*beta_2+s2*beta_1)/(beta_1-beta_2);
[t,x]=ode45(f,[1,3],[alfa,s]);
plot(t, x(:,1))
hold off
legend('-1.5','-3.0','s','location','northwest')
grid on
xlabel('x')
ylabel('y')
title('Condiciones en los extremos')

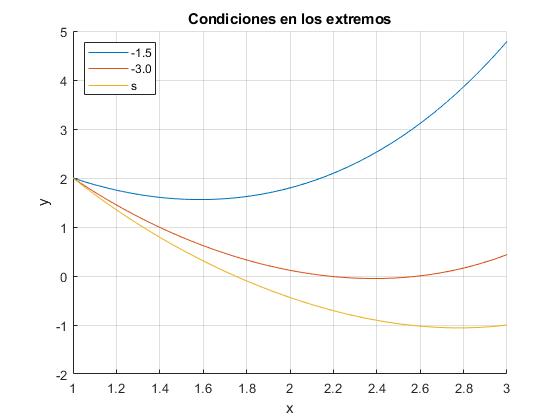
Cuando la ecuación diferencial es lineal acertamos en el 'blanco' (extremo derecho) al tercer intento

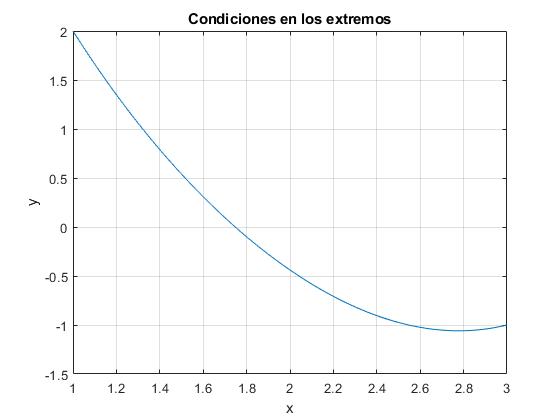
Resolvemos la ecuación diferencial utilizando el procedimiento bvp4c de MATLAB

function ecuacion_diferencial_3
    solinit = bvpinit(linspace(1,3,5), [0,-1]);
    sol = bvp4c(@f, @extremos, solinit);
    t=linspace(1,3);
    x = deval(sol,t);
    plot(t,x(1,:));
    grid on
    xlabel('x')
    ylabel('y')
    title('Condiciones en los extremos')
    
%ecuación diferencial
    function dx = f(t,x)
        dx = [x(2), (1-t/5)*x(1)+t];
    end
%condiciones en los extremos
    function res = extremos(xa,xb)
        res = [xa(1)-2, xb(1)+1];
    end
end

Ecuaciones diferenciales no lineales

Sea la ecuación diferencial con las condiciones en los extremos que se especifican

${\displaystyle \begin{array}{l}\frac{d^{2}y}{d{x}^2}-\frac{3}{2}{y}^2=\mathrm{0,}0\le x\le 1\\ y(0)=\mathrm{4,}y(1)=1\end{array}}$

Resolvemos la ecuación diferencial en el intervalo [0,1] con las condiciones iniciales ${y(0)=\mathrm{4,}\frac{dy}{dx}|}_{x=0}=s$ .Vamos cambiando s, representando la función F(s)=y(b,s)-1

alfa=4; %en x=0
beta=1; %en x=1
f=@(t,x) [x(2); 3*x(1)^2/2]; 
ss=linspace(-50,0,100);
fs=zeros(1,length(ss));
i=1;
for s=ss
    [t,x]=ode45(f,[0,1],[alfa,s]);
    fs(i)=x(end,1)-beta;
    i=i+1;
end
hold on
plot(ss, fs)
grid on
xlabel('s')
ylabel('F(s)')
title('Ceros')

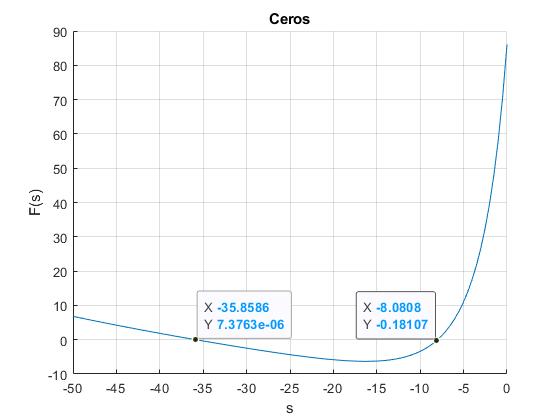
Vemos que la función F(s) se anula para dos valores de s, el primero próximo a s=-35.8 y el segundo próximo a s=-8.1

Aplicamos el procedimiento del punto medio para obtener la primera raíz, que se encuentra en el intervalo (-40,-20)

alfa=4; %en x=0
beta=1; %en x=1
f=@(t,x) [x(2); 3*x(1)^2/2]; 
a=-40; %intervalo dónde se encuentra la pimera raíz
b=-20;
CERO=1e-10;
ERROR=0.001;
MAXITER=100;
    for i=1:MAXITER
        m=(a+b)/2;
        [t,x]=ode45(f,[0,1],[alfa,a]);
        ya=x(end,1)-beta;
       [t,x]=ode45(f,[0,1],[alfa,m]);
        ym=x(end,1)-beta;
         if abs(ym)<CERO           
            break
         elseif abs((a-b)/m)<ERROR     
            break
         elseif (ya*ym)<0     
            b=m;
         else
            a=m;
         end
    end
    if(i==MAXITER) 
        error('no se ha encontrado la raiz')
    end
    disp(m)

 -35.8496

La segunda raíz se encuentra en el intervalo (-15,-5), cambiamos los valores de las variables a y b, obteniendo

  -8.0005

Representamos las dos posibles soluciones de la ecuación diferencial no lineal

alfa=4; %en x=0
f=@(t,x) [x(2); 3*x(1)^2/2]; 
hold on
for s=[-35.8496,-8.0005]
    [t,x]=ode45(f,[0,1],[alfa,s]);
    plot(t, x(:,1))
end
hold off
grid on
legend('-35.8496','-8.0005')
xlabel('x')
ylabel('y')
title('Condiciones en los extremos')

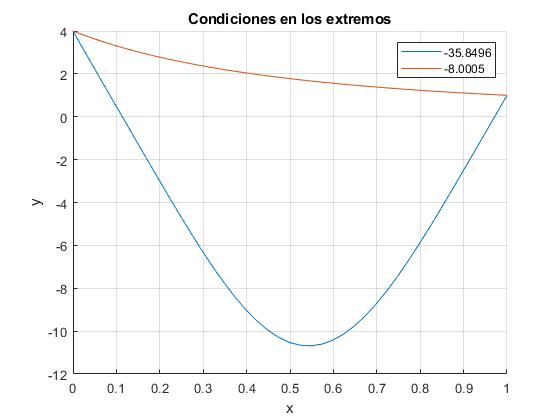
Resolvemos la ecuación diferencial utilizando el procedimiento bvp4c de MATLAB

function ecuacion_diferencial_4
    solinit = bvpinit(linspace(0,1,5), [-10,1]);
    sol1 = bvp4c(@f, @extremos, solinit);
    solinit = bvpinit(linspace(0,1,5), [4,1]);
    sol2 = bvp4c(@f, @extremos, solinit);
    t=linspace(0,1);
    x = deval(sol1,t);
    hold on
    plot(t,x(1,:));
    x = deval(sol2,t);
    plot(t,x(1,:));
    hold off
    grid on
    xlabel('x')
    ylabel('y')
    title('Condiciones en los extremos')
    
%ecuación diferencial
    function dx = f(~,x)
        dx = [x(2), 3*x(1)^2/2];
    end
%condiciones en los extremos
    function res = extremos(xa,xb)
        res = [xa(1)-4, xb(1)-1];
    end
end

Método de las diferencias finitas

Se divide el intervalo [a, b] en N partes iguales de longitud h=(b-a)/N. Las abscisas de cada uno de sus extremos son x_i=a+i·h, i=0,1, ...N

Reemplazamos las derivadas por diferencias finitas utilizando el desarrollo en serie de Taylor de una función alrededor de x_i

${\displaystyle y(x)=y(x_i)+(x-x_i){\frac{dy}{dx}|}_{x_i}+\frac{{\left(x-x_i\right)}^2}{2!}{\frac{d^{2}y}{d{x}^2}|}_{x_i}+\mathrm{....}}$

• Si x=x_i+1=x_i+h

${\displaystyle y(x_{i+1})=y(x_i)+h{\frac{dy}{dx}|}_{x_i}+\frac{h^2}{2}{\frac{d^{2}y}{d{x}^2}|}_{x_i}+\frac{h^3}{6}{\frac{d^{3}y}{d{x}^3}|}_{x_i}+\mathrm{...}}$

• Si x=x_i-1=x_i-h

${\displaystyle y(x_{i-1})=y(x_i)-h{\frac{dy}{dx}|}_{x_i}+\frac{h^2}{2}{\frac{d^{2}y}{d{x}^2}|}_{x_i}-\frac{h^3}{6}{\frac{d^{3}y}{d{x}^3}|}_{x_i}+\mathrm{...}}$

En este sistema de dos ecuaciones, despejamos la derivada primera y la derivada segunda en x_i

${\displaystyle \begin{array}{l}{\frac{dy}{dx}|}_{x_i}\approx \frac{y(x_{i+1})-y(x_{i-1})}{2h}\\ {\frac{d^{2}y}{d{x}^2}|}_{x_i}\approx \frac{y(x_{i+1})+y(x_{i-1})-2y(x_i)}{h^2}\end{array}}$

Ecuación diferencial lineal

Sea la ecuación diferencial lineal con condiciones en los extremos a y b

${\displaystyle \begin{array}{l}\frac{d^{2}y}{d{x}^2}+p(x)\frac{dy}{dx}+q(x)y+r(x)=0\\ y(a)=\alpha ,y(b)=\beta \end{array}}$

Introducimos la notación y(x_i)=y_i, p(x_i)=p_i, q(x_i)=q_i y r(x_i)=r_i.Transformamos la ecuación diferencial en una ecuación en diferencias finitas

${\displaystyle \begin{array}{l}{y}_0=\alpha \\ \frac{y_{i+1}+y_{i-1}-2y_i}{h^2}+p_i\frac{y_{i+1}-y_{i-1}}{2h}+q_i{y}_i+r_i=\mathrm{0,}i=\mathrm{1,2,3...}N-1\\ y_N=\beta \end{array}}$

Agrupando términos, obtenemos un sistema de N-1 ecuaciones con N-1 incógnitas

${\displaystyle \left(1+\frac{h}{2}{p}_i\right)y_{i+1}+\left(q_i{h}^2-2\right)y_i+\left(1-\frac{h}{2}{p}_i\right)y_{i-1}+h^2{r}_i=\mathrm{0,}i=\mathrm{1,2...}N-1}$

En forma matricial

${\displaystyle \left(\begin{array}{cccccccccc}{q}_1{h}^2-2& 1+\frac{h}{2}{p}_1& 0& 0& 0& 0& \mathrm{...}& 0& 0& 0\\ 1-\frac{h}{2}{p}_2& q_2{h}^2-2& 1+\frac{h}{2}{p}_2& 0& 0& 0& \mathrm{...}& 0& 0& 0\\ 0& 1-\frac{h}{2}{p}_3& q_3{h}^2-2& 1+\frac{h}{2}{p}_3& 0& 0& \mathrm{...}& 0& 0& 0\\ \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}\\ 0& 0& 0& 0& 0& 0& \mathrm{...}& 1-\frac{h}{2}{p}_{N-2}& q_{N-2}{h}^2-2& 1+\frac{h}{2}{p}_{N-2}\\ 0& 0& 0& 0& 0& 0& \mathrm{...}& 0& 1-\frac{h}{2}{p}_{N-1}& q_{N-1}{h}^2-2\end{array}\right)\left(\begin{array}{c}{y}_1\\ y_2\\ y_2\\ \mathrm{....}\\ y_{N-2}\\ y_{N-1}\end{array}\right)=\left(\begin{array}{c}-h^2{r}_1-\left(1-\frac{h}{2}{p}_1\right)\alpha \\ -h^2{r}_2\\ -h^2{r}_2\\ \mathrm{...}\\ -h^2{r}_{N-2}\\ -h^2{r}_{N-1}-\left(1+\frac{h}{2}{p}_{N-1}\right)\beta \end{array}\right)}$

Ejemplo 1

Resolvemos la ecuación diferencial lineal con condiciones en los extremos

${\displaystyle \begin{array}{l}\frac{d^{2}y}{d{x}^2}+(1+x^2)y+1=0\\ y(-1)=\mathrm{0,}y(1)=0\end{array}}$

Lo sustituimos por un sistema de N-1 ecuaciones con N-1 incógnitas, del siguiente modo

${\displaystyle \begin{array}{l}{x}_i=-1+ih\{\begin{array}{l}{p}_i=0\\ q_i=1+x_i^2\\ r_i=1\end{array}\\ \alpha =\mathrm{0,}\beta =0\end{array}}$

que en forma matricial se expresa

${\displaystyle \left(\begin{array}{cccccccccc}{q}_1{h}^2-2& 1& 0& 0& 0& 0& \mathrm{...}& 0& 0& 0\\ 1& q_2{h}^2-2& 1& 0& 0& 0& \mathrm{...}& 0& 0& 0\\ 0& 1& q_3{h}^2-2& 1& 0& 0& \mathrm{...}& 0& 0& 0\\ \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}\\ 0& 0& 0& 0& 0& 0& \mathrm{...}& 1& q_{N-2}{h}^2-2& 1\\ 0& 0& 0& 0& 0& 0& \mathrm{...}& 0& 1& q_{N-1}{h}^2-2\end{array}\right)\left(\begin{array}{c}{y}_1\\ y_2\\ y_2\\ \mathrm{....}\\ y_{N-2}\\ y_{N-1}\end{array}\right)=\left(\begin{array}{c}-h^2\\ -h^2\\ -h^2\\ \mathrm{...}\\ -h^2\\ -h^2\end{array}\right)}$

MATLAB facilita el trabajo con matrices: crear matrices, acceder a sus elementos, etc. Una vez que hemos definido el vector A de los coeficientes y el vector B de los términos independientes, despejamos el vector Y de las incógnitas, A·Y=B, utilizando el operador división por la izquierda '\'

alfa=0; %en x=-1
beta=0; %en x=1
N=50;
h=2/50;
A=diag(ones(1,N-2),1)+diag(ones(1,N-2),-1);
for i=1:N-1
    A(i,i)=(1+(-1+i*h)^2)*h^2-2;
end
B=ones(N-1,1)*(-h^2);
Y=A\B;
plot(-1+(0:N)*h, [alfa, Y',beta],'-ro','markersize',3,'markeredgecolor'
,'r','markerfacecolor','r')
xlabel('x')
ylabel('y')
grid on
title('Diferencias finitas')

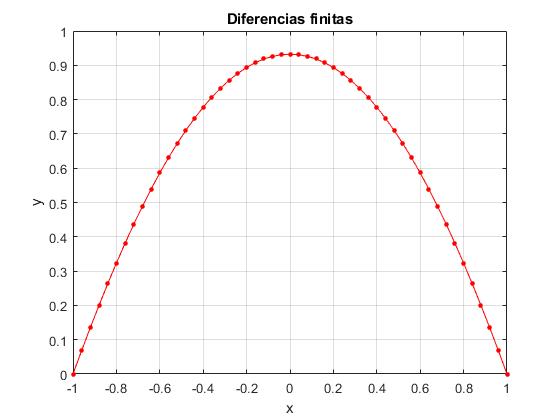
Resolvemos la ecuación diferencial utilizando el procedimiento bvp4c de MATLAB

function ecuacion_diferencial_5
    solinit = bvpinit(linspace(-1,1,5), [0,0]);
    sol = bvp4c(@f, @extremos, solinit);
    t=linspace(-1,1);
    x = deval(sol,t);
    plot(t,x(1,:));
    grid on
    xlabel('x')
    ylabel('y')
    title('Condiciones en los extremos')
    
%ecuación diferencial
    function dx = f(t,x)
        dx = [x(2), -1-(1+t^2)*x(1)];
    end
%condiciones en los extremos
    function res = extremos(xa,xb)
        res = [xa(1), xb(1)];
    end
end

Ejemplo 2

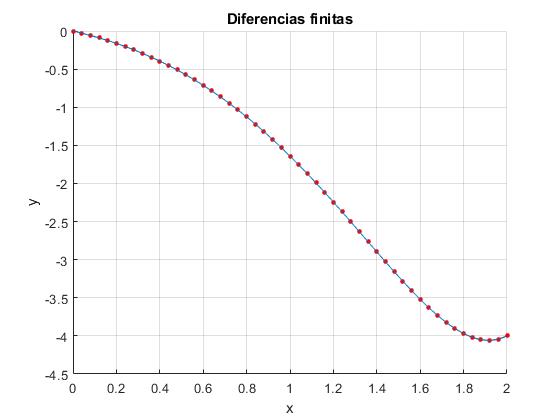
Resolvemos la ecuación diferencial lineal con condiciones en los extremos

${\displaystyle \begin{array}{l}\frac{d^{2}y}{d{x}^2}-2\frac{dy}{dx}+y-x{e}^x+x=0\\ y(0)=\mathrm{0,}y(2)=-4\end{array}}$

Esta ecuación diferencial tiene solución analítica

>> syms x;
>> y=dsolve('D2y-2*Dy+y-x*exp(x)+x',x);
>> simplify(y)
ans =(x^3*exp(x))/6 - x + C5*exp(x) + C6*x*exp(x) - 2

${\displaystyle y=\frac{1}{6}{x}^3{e}^x-x+A{e}^x+Bx{e}^x-2}$

Determinamos los coeficientes A y B a partir de las condiciones en los extremos: A=2, B=-5/3

${\displaystyle y=\left(\frac{1}{6}{x}^3-\frac{5}{3}x+2\right)e^x-x-2}$

Lo sustituimos por un sistema de N-1 ecuaciones con N-1 incógnitas, del siguiente modo

${\displaystyle \begin{array}{l}{x}_i=ih\{\begin{array}{l}{p}_i=-2\\ q_i=1\\ r_i=-x_i{e}^{x_i}+x_i\end{array}\\ \alpha =\mathrm{0,}\beta =-4\end{array}}$

que en forma matricial se expresa

${\displaystyle \left(\begin{array}{cccccccccc}{h}^2-2& 1-h& 0& 0& 0& 0& \mathrm{...}& 0& 0& 0\\ 1+h& h^2-2& 1-h& 0& 0& 0& \mathrm{...}& 0& 0& 0\\ 0& 1+h& h^2-2& 1-h& 0& 0& \mathrm{...}& 0& 0& 0\\ \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}\\ 0& 0& 0& 0& 0& 0& \mathrm{...}& 1+h& h^2-2& 1-h\\ 0& 0& 0& 0& 0& 0& \mathrm{...}& 0& 1+h& h^2-2\end{array}\right)\left(\begin{array}{c}{y}_1\\ y_2\\ y_2\\ \mathrm{....}\\ y_{N-2}\\ y_{N-1}\end{array}\right)=\left(\begin{array}{c}-h^2{r}_1-\left(1-h\right)\alpha \\ -h^2{r}_2\\ -h^2{r}_2\\ \mathrm{...}\\ -h^2{r}_{N-2}\\ -h^2{r}_{N-1}-\left(1+h\right)\beta \end{array}\right)}$

Observamos la coincidencia entre la solución analítica y numérica

alfa=0; %en x=0
beta=-4; %en x=2
N=50;
h=2/N;
A=diag((1-h)*ones(1,N-2),1)+diag((1+h)*ones(1,N-2),-1)+diag((h^2-2)*ones(1,N-1));
B=zeros(N-1,1);
for i=1:N-1
    x=i*h;
    B(i)=-h^2*(-x*exp(x)+x);
end
B(1)=B(1)-(1+h)*alfa;
B(N-1)=B(N-1)-(1-h)*beta;
Y=A\B;
hold on
plot((0:N)*h, [alfa Y',beta],'-ro','markersize',3,'markeredgecolor',
'r','markerfacecolor','r')
ye=@(x) (x.^3/6-5*x/3+2).*exp(x)-x-2; %exacta
fplot(ye,[0,2])
hold off
xlabel('x')
ylabel('y')
grid on
title('Diferencias finitas')

Resolvemos la ecuación diferencial utilizando el procedimiento bvp4c de MATLAB

function ecuacion_diferencial_6
    solinit = bvpinit(linspace(0,2,5), [0,0]);
    sol = bvp4c(@f, @extremos, solinit);
    t=linspace(0,2);
    x = deval(sol,t);
    plot(t,x(1,:));
    grid on
    xlabel('x')
    ylabel('y')
    title('Condiciones en los extremos')
    
%ecuación diferencial
    function dx = f(t,x)
        dx = [x(2), 2*x(2)-x(1)+t*exp(t)-t];
    end
%condiciones en los extremos
    function res = extremos(xa,xb)
        res = [xa(1), xb(1)+4];
    end
end

Ecuación diferencial no lineal

Este tipo de ecuaciones diferenciales con condiciones en los extremos son mucho más difíciles de resolver

${\displaystyle \begin{array}{l}\frac{d^{2}y}{d{x}^2}=f\left(x,y,\frac{dy}{dx}\right)\\ y(a)=\alpha ,y(b)=\beta \end{array}}$

Sustituimos por un sistema de N-1 ecuaciones con N-1 incógnitas, del siguiente modo

${\displaystyle \begin{array}{l}{y}_0=\alpha \\ \frac{y_{i+1}+y_{i-1}-2y_i}{h^2}=f\left(x_i,y_i,\frac{y_{i+1}-y_{i-1}}{2h}\right),i=\mathrm{1,2,3...}N-1\\ y_N=\beta \end{array}}$

de forma explícita

${\displaystyle \{\begin{array}{l}{y}_2-2y_1+\alpha -h^{2}f\left(x_1,y_{\mathrm{1,}}\frac{y_2-\alpha }{2h}\right)=0\\ y_3-2y_2+y_1-h^{2}f\left(x_2,y_{\mathrm{2,}}\frac{y_3-y_1}{2h}\right)=0\\ \mathrm{...}\\ y_{N-1}-2y_{N-2}+y_{N-3}-h^{2}f\left(x_{N-2},y_{N-\mathrm{2,}}\frac{y_{N-1}-y_{N-3}}{2h}\right)=0\\ \beta -2y_{N-1}+y_{N-2}-h^{2}f\left(x_{N-1},y_{N-\mathrm{1,}}\frac{\beta -y_{N-2}}{2h}\right)=0\end{array}}$

Ejemplo

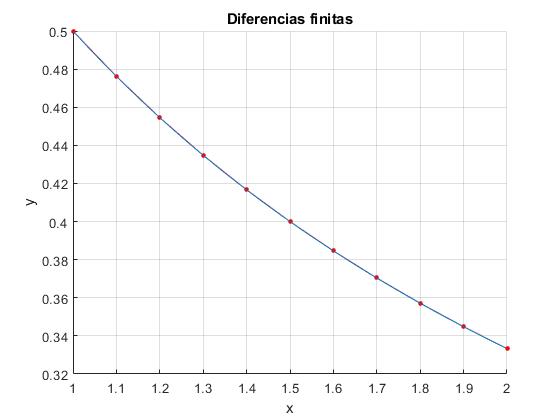
Resolvemos la ecuación diferencial no lineal con condiciones en los extremos

${\displaystyle \begin{array}{l}\frac{d^{2}y}{d{x}^2}=y^3-y\frac{dy}{dx}\\ y(1)=\frac{1}{2},y(2)=\frac{1}{3}\end{array}}$

La solución analítica es

>> dsolve('D2y-y^3+y*Dy',x)
ans =   -1/(C23 - x)
 -1/(C20 + x/2)

${\displaystyle y=\frac{-1}{A-x}}$

Determinamos A sabiendo que y(1)=1/2, A=-1

${\displaystyle y=\frac{1}{1+x}}$

En el otro extremo del intervalo, se cumple que y(2)=1/3

Comprobamos que y=1/(1+x) es solución de la ecuación diferencial

>> syms x;
>> y=1/(1+x);
>> diff(y,x,2)-y^3+y*diff(y,x)
ans =0

El sistema de N-1 ecuaciones con N-1 incógnitas, es

${\displaystyle \{\begin{array}{l}{y}_2-2y_1+\frac{1}{2}-h^2\left(y_1^3-y_1\frac{y_2-\frac{1}{2}}{2h}\right)=0\\ y_{i+1}-2y_i+y_{i-1}-h^2\left(y_i^3-y_i\frac{y_{i+1}-y_{i-1}}{2h}\right)=\mathrm{0,}i=\mathrm{2,3,...}N-2\\ \frac{1}{3}-2y_{N-1}+y_{N-2}-h^2\left(y_{N-1}^3-y_{N-1}\frac{\frac{1}{3}-y_{N-2}}{2h}\right)=0\end{array}}$

Vamos a utilizar el procedimiento de Newton-Raphson para resolver este sistema de ecuaciones no lineales

${\displaystyle \{\begin{array}{l}{g}_1(y_1,y_2\mathrm{,...,}{y}_{N-1})=0\\ g_2(y_1,y_2\mathrm{,...,}{y}_{N-1})=0\\ \mathrm{....}\\ g_{N-1}(y_1,y_2\mathrm{,...,}{y}_{N-1})=0\end{array}}$

El procedimiento se escribe

${\displaystyle \left(\begin{array}{c}{y}_1^{\text{'}}\\ y_2^{\text{'}}\\ \mathrm{...}\\ y_{N-1}^{\text{'}}\end{array}\right)=\left(\begin{array}{c}{y}_1\\ y_2\\ \mathrm{...}\\ y_{N-1}\end{array}\right)-{\left(\begin{array}{cccc}\frac{\partial g_1}{\partial y_1}& \frac{\partial g_1}{\partial y_2}& \mathrm{...}& \frac{\partial g_1}{\partial y_{N-1}}\\ \frac{\partial g_2}{\partial y_1}& \frac{\partial g_2}{\partial y_2}& \mathrm{...}& \frac{\partial g_2}{\partial y_{N-1}}\\ \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}\\ \frac{\partial g_{N-1}}{\partial y_1}& \frac{\partial g_{N-1}}{\partial y_2}& \mathrm{...}& \frac{\partial g_{N-1}}{\partial y_{N-1}}\end{array}\right)}^{-1}\left(\begin{array}{c}{g}_1(y_1,y_2\mathrm{...}{y}_{N-1})\\ g_2(y_1,y_2\mathrm{...}{y}_{N-1})\\ \mathrm{...}\\ g_{N-1}(y_1,y_2\mathrm{...}{y}_{N-1})\end{array}\right)}$

o bien, Y'=Y-J\G, utilizando el operador MATLAB, división por la izquierda \. Se obtiene el nuevo vector Y' de la izquierda, a partir del Y previo, a la derecha de la igualdad

El vector G son las ecuaciones (sin la igauldad a cero) y la matriz J es

${\displaystyle \left(\begin{array}{cccccccccc}-2-h^2\left(3y_1^2-\frac{y_2-\frac{1}{2}}{2h}\right)& 1+h\frac{y_1}{2}& 0& 0& 0& \mathrm{...}& 0& 0& 0& 0\\ 1-h\frac{y_2}{2}& -2-h^2\left(3y_2^2-\frac{y_3-y_1}{2h}\right)& 1+h\frac{y_2}{2}& 0& 0& \mathrm{...}& 0& 0& 0& 0\\ 0& 1-h\frac{y_3}{2}& -2-h^2\left(3y_2^2-\frac{y_3-y_1}{2h}\right)& 1+h\frac{y_3}{2}& 0& \mathrm{...}& 0& 0& 0& 0\\ \mathrm{...}& \mathrm{...}& \mathrm{....}& \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}\\ \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}\\ 0& 0& 0& 0& 0& \mathrm{...}& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& \mathrm{...}& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& \mathrm{...}& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& \mathrm{...}& 0& 1-h\frac{y_{N-2}}{2}& -2-h^2\left(3y_{N-2}^2-\frac{y_{N-1}-y_{N-3}}{2h}\right)& 1+h\frac{y_{N-2}}{2}\\ 0& 0& 0& 0& 0& \mathrm{...}& 0& 0& 1-h\frac{y_{N-1}}{2}& -2-h^2\left(3y_{N-1}^2-\frac{\frac{1}{3}-y_{N-2}}{2h}\right)\end{array}\right)}$

Nota: Esta expresión se muestra muy pequeña para que quepa en la página, pero se puede aumentar, utilizando el botón derecho del ratón y seleccionando en el menú flotante, Math Settings/Scale all Math...

alfa=1/2; %en x=1
beta=1/3; %en x=2
N=10;
h=1/N;
y=ones(N-1,1);
G=zeros(N-1,1);
J=zeros(N-1);
for k=1:100
    G(1)=y(2)-2*y(1)+alfa-h^2*(y(1)^3-y(1)*(y(2)-alfa)/(2*h));
    for i=2:N-2
        G(i)=y(i+1)-2*y(i)+y(i-1)-h^2*(y(i)^3-y(i)*(y(i+1)-y(i-1))/(2*h));
    end
    G(N-1)=beta-2*y(N-1)+y(N-2)-h^2*(y(N-1)^3-y(N-1)*(beta-y(N-2))/(2*h));
    J(1,1)=-2-h^2*(3*y(1)^2-(y(2)-alfa)/(2*h));
    J(N-1,N-1)=-2-h^2*(3*y(N-1)^2-(beta-y(N-2))/(2*h));
    for i=2:N-2
        J(i,i)=-2-h^2*(3*y(i)^2-(y(i+1)-y(i-1))/(2*h));
    end  
    for i=2:N-1
        J(i, i-1)=1-y(i)*h/2;
    end
    for i=1:N-2
        J(i, i+1)=1+y(i)*h/2;
    end
    dy=-J\G;
    if sqrt(norm(dy)/norm(y+dy))<0.0001
        disp('Solución')
        disp(y+dy)
        break;
    end
    y=y+dy;
end
if k==100
    disp('Se ha soprepasado el número de iteracciones');
end
hold on
plot(1+(0:N)*h, [alfa y',beta],'-ro','markersize',3,'markeredgecolor',
'r','markerfacecolor','r')
ye=@(x) 1./(x+1); %exacta
fplot(ye,[1,2])
hold off
xlabel('x')
ylabel('y')
grid on
title('Diferencias finitas')

Solución
    0.4762
    0.4546
    0.4348
    0.4167
    0.4000
    0.3846
    0.3704
    0.3571
    0.3448

Observamos la coincidencia entre la solución analítica y numérica

Resolvemos la ecuación diferencial utilizando el procedimiento bvp4c de MATLAB

function ecuacion_diferencial_7
    solinit = bvpinit(linspace(1,2,5), [0,-1]);
    sol = bvp4c(@f, @extremos, solinit);
    t=linspace(1,2);
    x = deval(sol,t);
    plot(t,x(1,:));
    grid on
    xlabel('x')
    ylabel('y')
    title('Condiciones en los extremos')
    
%ecuación diferencial
    function dx = f(~,x)
        dx = [x(2), x(1)^3-x(1)*x(2)];
    end
%condiciones en los extremos
    function res = extremos(xa,xb)
        res = [xa(1)-1/2, xb(1)-1/3];
    end
end

Referencias

James V. Lambers, Amber C. Sumner. Explorations in Numerical Analysis. December 20, 2016. pp. 343-352