Procedimiento de Picard

Vamos a resolver la ecuación diferencial

${\displaystyle \frac{dx}{dt}=f(t,x)}$

con la condición inicial, t=t₀, x=x₀

Integrando

${\displaystyle \begin{array}{l}{\displaystyle \underset{x_0}{\overset{x}{\int }}dx}={\displaystyle \underset{t_0}{\overset{t}{\int }}f(t,x)dt}\\ x=x_0+{\displaystyle \underset{t_0}{\overset{t}{\int }}f(t,x)dt}\end{array}}$

Aproximaciones sucesivas

${\displaystyle \begin{array}{l}{x}^{(1)}=x_0+{\displaystyle \underset{t_0}{\overset{t}{\int }}f(t,x^{(0)})dt},x^{(0)}=x_0\\ x^{(2)}=x_0+{\displaystyle \underset{t_0}{\overset{t}{\int }}f(t,x^{(1)})dt}\\ \mathrm{....}\\ x^{(n)}=x_0+{\displaystyle \underset{t_0}{\overset{t}{\int }}f(t,x^{(n-1)})dt}\end{array}}$

Ejemplo. Sea la ecuación diferencial

${\displaystyle \frac{dx}{dt}=x+t}$

Con la condición inicial t=0, x=1

• Solución analítica

La solución de la ecuación diferencial homogénea es

${\displaystyle \begin{array}{l}\frac{dx}{dt}-x=0\\ x_h=A{e}^t\end{array}}$

La solución particular es x_p=Bt+C. Introduciendo en la ecuación diferencial

${\displaystyle \begin{array}{l}\frac{dx}{dt}-x=t\\ B-Bt-C=t,\{\begin{array}{l}B-C=0\\ B=-1\end{array}\\ x_p=Bt+C=-t+1\end{array}}$

La solución completa de la ecuación diferencial es

${\displaystyle \begin{array}{l}\frac{dx}{dt}-x=t\\ x=x_h+x_p=A{e}^t-t-1\end{array}}$

El coeficiente A se determina a partir de la condición inicial, t=0, x=1

${\displaystyle \begin{array}{l}1=A-\mathrm{1,}A=2\\ x=2e^t-t-1\end{array}}$

• Solución aproximada

${\displaystyle \begin{array}{l}{x}^{(1)}=1+{\displaystyle \underset{0}{\overset{t}{\int }}\left(t+1\right)dt}=\frac{t^2}{2}+t+1\\ x^{(2)}=1+{\displaystyle \underset{0}{\overset{t}{\int }}\left(t+\left(\frac{1}{2}{t}^2+t+1\right)\right)dt}=1+{\displaystyle \underset{0}{\overset{t}{\int }}\left(\frac{1}{2}{t}^2+2t+1\right)dt}=\frac{t^3}{6}+t^2+t+1\\ x^{(3)}=1+{\displaystyle \underset{0}{\overset{t}{\int }}\left(t+\left(\frac{1}{6}{t}^3+t^2+t+1\right)\right)dt}=1+{\displaystyle \underset{0}{\overset{t}{\int }}\left(\frac{1}{6}{t}^3+t^2+2t+1\right)dt}=\frac{t^4}{24}+\frac{t^3}{3}+t^2+t+1\\ x^{(4)}=1+{\displaystyle \underset{0}{\overset{t}{\int }}\left(t+\left(\frac{1}{24}{t}^4+\frac{1}{3}{t}^3+t^2+t+1\right)\right)dt}=1+{\displaystyle \underset{0}{\overset{t}{\int }}\left(\frac{1}{24}{t}^4+\frac{1}{3}{t}^3+t^2+2t+1\right)dt}=\frac{t^5}{120}+\frac{t^4}{12}+\frac{t^3}{3}+t^2+t+1\\ x^{(5)}=1+{\displaystyle \underset{0}{\overset{t}{\int }}\left(t+\left(\frac{1}{120}{t}^5+\frac{1}{12}{t}^4+\frac{1}{3}{t}^3+t^2+t+1\right)\right)dt}=1+{\displaystyle \underset{0}{\overset{t}{\int }}\left(\frac{1}{120}{t}^5+\frac{1}{12}{t}^4+\frac{1}{3}{t}^3+t^2+2t+1\right)dt}=\frac{t^6}{720}+\frac{t^5}{60}+\frac{t^4}{12}+\frac{t^3}{3}+t^2+t+1\end{array}}$

Representamos la solución exacta y aproximada en el intervalo [-3,3]

syms t;
x=1; %para t=0, condición inicial
for n=1:5
    x=1+int(@(t) t+x, 0,t);
    x=simplify(x);
end
hold on
disp(x)
fplot(x,[-3,3]) %aproximada
x=2*exp(t)-t-1;
fplot(x,[-3,3]) %exacta
hold off
grid on
xlabel('t')
ylabel('x')
legend('aproximada', 'exacta')
title('Solución exacta y aproximada')

t^6/720 + t^5/60 + t^4/12 + t^3/3 + t^2 + t + 1



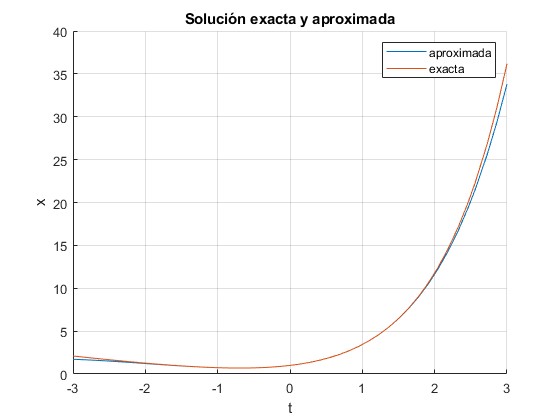
Desarrollamos en serie la exponencial e^t en la solución exacta y la comparamos con la solución aproximada

>> syms t;
>> 2*taylor(exp(t),t,0,'order',7)-t-1
 ans =t^6/360 + t^5/60 + t^4/12 + t^3/3 + t^2 + t + 1

Vemos que coinciden hasta el término en t⁵

El procedimiento de Picard está limitado a ecuaciones diferenciales que se pueden integrar fácilmente en las sucesivas aproximaciones. Por ejemplo, la ecuación diferencial

${\displaystyle \frac{dx}{dt}=\frac{x-t}{x+t}}$

Con la condición inicial, t=0, x=1

Solamente se puede obtener la primera aproximación

${\displaystyle \begin{array}{l}{x}^{(1)}=1+{\displaystyle \underset{0}{\overset{t}{\int }}\frac{1-t}{1+t}dt}=1+{\displaystyle \underset{0}{\overset{t}{\int }}\left(-1+\frac{2}{1+t}\right)dt=1-t+2\ln (1+t)}\\ x^{(2)}=1+{\displaystyle \underset{0}{\overset{t}{\int }}\left(\frac{1-t+2\ln (1+t)-t}{1-t+2\ln (1+t)+t}\right)dt}=1+{\displaystyle \underset{0}{\overset{t}{\int }}\left(\frac{1-2t+2\ln (1+t)}{1+2\ln (1+t)}\right)dt}=1+{\displaystyle \underset{0}{\overset{t}{\int }}\left(1-\frac{2t}{1+2\ln (1+t)}\right)dt}\end{array}}$

Esta integral es muy difícil de resolver

Método de Euler

Vamos aresolver la ecuación diferencial de primer orden

${\displaystyle \frac{dx}{dt}=f(t,x)}$

con con la condición inicial de que en el instante t₀ la posición es x₀

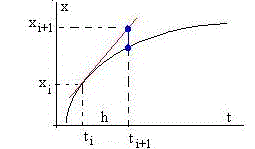
La primera derivada nos permite conocer la posición x_i+1 en el instante t_i+1, a partir de la posición x_i en el instante t_i de acuerdo a la fórmula siguiente. La línea de color rojo es la tangente a la curva en el instante t_i

x_i+1=x_i+f(t_i,x_i)h

El procedimiento de Euler produce un error que se acumula a cada paso h de integración, que es el segmento en color azul que une los dos puntos en la figura.

Escribimos una función denominada euler, a la que le pasaremos:

• la función f(t,x),
• la condición inicial de que en el instante t₀ la posición es x₀,
• el instante final t_f
• el número de pasos de integración n

y nos devolverá un vector t y su correspondiente vector x.

function [t,x] =euler(f,t0,tf,x0,n)
      h=(tf-t0)/n;
      t=t0:h:tf;
      x=zeros(n+1,1); %reserva memoria para n+1 elementos del vector x
      x(1)=x0;
      for i=1:n
          x(i+1)=x(i)+f(t(i),x(i))*h;
      end
end

Supongamos que queremos integrar la ecuación diferencial

${\displaystyle \frac{dx}{dt}=\cos t}$

con las condición inicial t=0, x=0.

${\displaystyle \begin{array}{l}x-0={\displaystyle \underset{0}{\overset{t}{\int }}\cos t·dt}\\ x=\sin t\end{array}}$

Tomamos un intervalo h=π/6, y construimos la siguiente tabla

Para aplicar el método de Euler precisamos de un paso h pequeño, incluso así los errores se van acumulando y al cabo de cierto tiempo la diferencia entre el valor exacto y el calculado es grande.

Escribimos un script en el que definiremos la función f(t,x), las condiciones iniciales y llamaremos a la función euler. Finalmente, representaremos gráficamente la solución exacta y la obtenida aplicando el método de Euler

tf=input('tiempo final, tf: ');
n=input('número de pasos, n: ');
f=@(t,x) cos(t); 
%condiciones iniciales
t0=0; 
x0=0;
[t,x]=euler(f,t0,tf,x0,n); 

hold on
plot(t,x,'b')
y=sin(t);
plot(t,y,'r')
xlabel('t')
ylabel('x')
grid on
legend('aproximada','exacta')
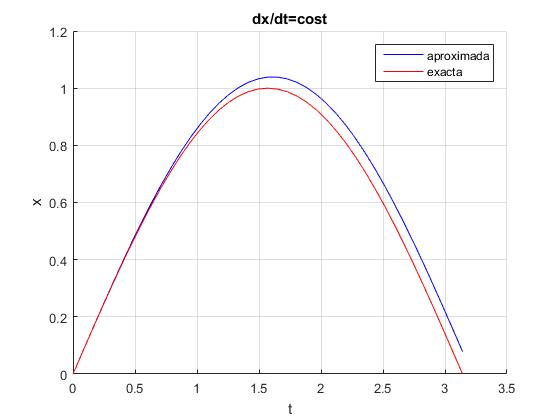
title('dx/dt=cost')
hold off

En la ventana de comandos corremos el script

tiempo final, tf: pi
número de pasos, n: 40

Apreciamos diferencias entre la solución exacta y la obtenida mediante integración numérica por el método de Euler

Método de Runge-Kutta

En esta sección vamos a estudiar la aplicación del método de Runge-Kutta a:

• Una ecuación diferencial de primer orden
• Un sistema de dos ecuaciones diferenciales de primer orden
• Una ecuación difrencial de segundo orden
• Un sistema de dos ecuaciones diferenciales de segundo orden

Ecuación diferencial de primer orden

Sea una ecuación diferencial de primer orden, con la condición inicial de que en el instante t₀ el valor inicial de x es x₀

Se elige una anchura de paso h y se calculan cuatro números k₁, k₂, k₃, k₄ de acuerdo con el procedimiento esquematizado en la tabla adjunta. Según el procedimiento ordinario de Runge-Kutta, a partir del valor de x en el instante t se determina el valor de x en el instante t+h mediante la fórmula que figura en la última fila de dicha tabla.

Definimos la función rk_1 que resuelve la ecuación diferencial de primer orden, cuando le pasamos:

• la función f(t,x),
• la condición inicial de que en el instante t₀el valor inicial es x₀,
• el instante final t_f
• el número de pasos de integración n comprendidos entre el instante inical t₀ y final t_f.

y nos devolverá un vector t y su correspondiente vector x.

function [t,x] =rk_1(f,t0,tf,x0,n)
    h=(tf-t0)/n;
    t=t0:h:tf;
    x=zeros(n+1,1); %reserva memoria para n elementos del vector x
    x(1)=x0;
    for i=1:n
        k1=h*f(t(i),x(i));
        k2=h*f(t(i)+h/2,x(i)+k1/2);
        k3=h*f(t(i)+h/2,x(i)+k2/2);
        k4=h*f(t(i)+h,x(i)+k3);
        x(i+1)=x(i)+(k1+2*k2+2*k3+k4)/6;
     end
end

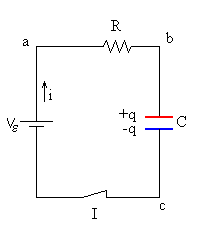
Considérese el circuito en serie de la figura. Inicialmente el condensador está descargado. Si se cierra el interruptor I la carga empieza a fluir produciendo corriente en el circuito, el condensador se empieza a cargar. Una vez que el condensador adquiere la carga máxima, la corriente cesa en el circuito.

${\displaystyle \begin{array}{l}R\frac{dq}{dt}=V_{\epsilon }-\frac{q}{C}\\ {\displaystyle \underset{0}{\overset{q}{\int }}\frac{dq}{C{V}_{\epsilon }-q}}=\frac{1}{RC}{\displaystyle \underset{0}{\overset{t}{\int }}dt}q=C{V}_{\epsilon }\left(1-\exp \left(\frac{-t}{RC}\right)\right)\end{array}}$

Escribimos un script para que realice las siguientes tareas:

1. Establezca, mediante comandos input:
• La resistencia R del circuito
• La capacidad C del condensador
• El tiempo final, tf
• el número de pasos, n.
2. Fije las condiciones iniciales, en el instante inicial t=0, el condensador está descargado x=0.
3. Defina la función f(t,x),
4. Llame al procedimiento numérico rk_1
5. Mediante el comando plot realice una representación gráfica de la solución numérica
6. Realice una representación gráfica de la solución exacta

Ejemplo: R=2.0, C=0.8, y tf=10.

V0=10;
R=input('Resistencia R: ');
C=input('Capacidad C: ');
tf=input('tiempo final, tf: ');
n=input('número de pasos, n: ');

f=@(t,x) V0/R-x/(R*C); 
%condiciones iniciales
t0=0; x0=0; 
[t,x]=rk_1(f,t0,tf,x0,n); 

hold on
plot(t,x,'b')
y=C*V0*(1-exp(-t/(R*C)));
plot(t,y,'r')
xlabel('t')
ylabel('q')
grid on
legend('aproximada','exacta','Location','Southeast')
title('Carga del condensador')
hold off

En la ventana de comandos corremos el script

Resistencia R: 2
Capacidad C: 0.8
tiempo final, tf: 10
número de pasos, n: 50

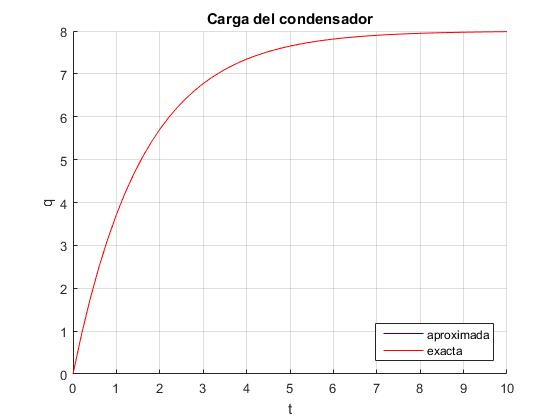
No se aprecia diferencia entre la solución exacta y la numérica, aplicando el procedimiento de Runge_Kutta.

Sistema de dos ecuaciones diferenciales de primer orden

El procedimiento de Runge-Kutta es igualmente efectivo en la resolución de un sistema de dos ecuaciones diferenciales de primer orden.

${\displaystyle \frac{dx}{dt}=f(t,x,y)\frac{dy}{dt}=g(t,x,y)}$

El procedimiento de aplicación del método de Runge-Kutta a cada una de las ecuaciones diferenciales, con las condición inicial siguiente, en el instante t₀

• el valor inicial de x es x₀
• el valor inicial de y es y₀

se esquematiza en la tabla adjunta. Como vemos además de los cuatro números k₁, k₂, k₃, k₄ para la primera ecuación diferencial precisamos otros cuatro números l₁, l₂, l₃, l₄ para la segunda ecuación diferencial. A partir del valor de x en el instante t, se determina el valor de x en el instante t+h, y a partir del valor de y en el instante t se determina el valor de y en el instante t+h mediante las fórmulas de la última fila de la tabla.

Definimos la función rk_2_1 que resuelve el sistema de dos ecuaciones diferenciales de primer orden, cuando le pasamos:

• las funciones f (t,x,y) y g(t,x,y)
• las condiciones iniciales (x₀,y₀) en el instante t₀
• el número n de pasos de integración entre t₀ y el tiempo final t_f

Nos devuelve los vectores x e y para cada instante que se guarda en el vector t comprendido entre el instante inicial t0 y el final tf.

function [t,x,y] =rk_2_1(f,g,t0,tf,x0,y0,n)
      h=(tf-t0)/n;
      t=t0:h:tf;
%reserva memoria para n+1 element(i)os del vect(i)or x(i)
      x=zeros(n+1,1); 
      y=zeros(n+1,1);
      x(1)=x0; y(1)=y0;
      
      for i=1:n
        k1=h*f(t(i),x(i),y(i));
        l1=h*g(t(i),x(i),y(i));
        k2=h*f(t(i)+h/2,x(i)+k1/2,y(i)+l1/2);
        l2=h*g(t(i)+h/2,x(i)+k1/2,y(i)+l1/2);
        k3=h*f(t(i)+h/2,x(i)+k2/2,y(i)+l2/2);
        l3=h*g(t(i)+h/2,x(i)+k2/2,y(i)+l2/2);
        k4=h*f(t(i)+h,x(i)+k3,y(i)+l3);
        l4=h*g(t(i)+h,x(i)+k3,y(i)+l3);
        
        x(i+1)=x(i)+(k1+2*k2+2*k3+k4)/6;
        y(i+1)=y(i)+(l1+2*l2+2*l3+l4)/6;        
      end
end

Consideremos una serie radioactiva de tres elementos A-->B-->C en la que, una sustancia radiactiva A se desintegra y se transforma en otra sustancia radiactiva B, que a su vez se desintegra y se transforma en una sustancia C estable. Las ecuaciones diferenciales que gobiernan el proceso y sus soluciones analíticas son, respectivamente,

${\displaystyle \begin{array}{l}\frac{dx}{dt}=-axx=x_0\exp (-at)\\ \frac{dy}{dt}=ax-byy=\frac{a}{b-a}{x}_0\left(\exp (-at)-\exp (-bt)\right)\end{array}}$

La solución analítica que aparece a la derecha, se ha obtenido con las condiciones iniciales t=0, x=x₀ e y=0. La segunda solución se obtiene siempre que a sea distinto de b. En el caso de que a sea igual a b, la solución analítica para y es

${\displaystyle y=x_{0}a\exp (-at)}$

La interpretación del sistema de ecuaciones diferenciales no es complicada. En la unidad de tiempo, desaparecen ax núcleos de la sustancia A al desintegrarse (primera ecuación). En la unidad de tiempo, se producen ax núcleos de la sustancia B y a su vez desaparecen bx núcleos de la sustancia B, que al desintegrarse se transforman en núcleos de la sustancia C estable (segunda ecuación).

Escribimos un script en el que definiremos las funciones f(t,x,y), g(t,x,y), las condiciones iniciales y llamaremos a la función rk_2_1

a=input('parámetro a: ');
b=input('parámetro b: ');
x0=input('valor inicial de x: ');
y0=input('valor inicial de y: ');
tf=input('tiempo final, tf: ');
n=input('número de pasos, n: ');
f=@(t,x,y) -a*x; 
g=@(t,x,y) a*x-b*y;
%condiciones iniciales
t0=0; 

[t,x,y]=rk_2_1(f,g,t0,tf,x0,y0,n);
hold on
plot(t,x,'b')
plot(t,y,'r')
xlabel('t')
ylabel('x,y')
grid on
legend('x(t)','y(t)')
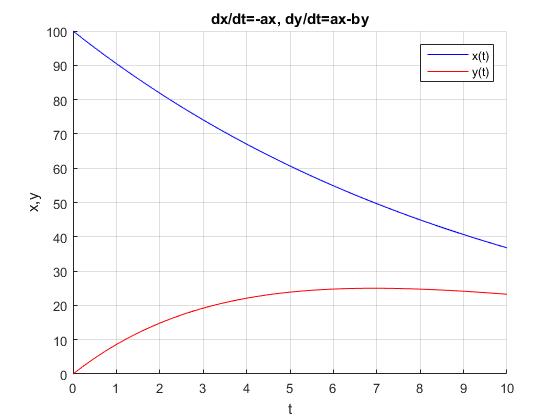
title('dx/dt=-ax, dy/dt=ax-by')
hold off

En la ventana de comandos corremos el script

parámetro a: 0.1
parámetro b: .2
valor inicial de x: 100
valor inicial de y: 0
tiempo final, tf: 10
número de pasos, n: 40

Ecuación diferencial de segundo orden

Existen muchas situaciones en las que es necesario resolver una ecuación diferencial de segundo orden.

${\displaystyle \frac{d^{2}x}{d{t}^2}=f(t,x,v)}$

con las condiciones iniciales

${\displaystyle x(t_0)=x_0{\left(\frac{dx}{dt}\right)}_{t_0}=v_0}$

Una ecuación diferencial de segundo orden es equivalente a un sistema de dos ecuaciones diferenciales de primer orden, por lo que aplicaremos el mismo esquema.

Definimos la función rk_2 que resuelve la ecuación diferencial de segundo orden, cuando le pasamos:

• la función f (t,x,v)
• las condiciones iniciales: posición inicial x₀ y velocidad inicial v₀ en el instante t₀
• el número n de pasos de integración entre t₀ y el tiempo final t_f

Nos devuelve los vectores de las posiciones x y las velocidades v para cada instante que se guarda en el vector t comprendido entre el instante inicial t0 y el final tf.

function [t,x,v] =rk_2(f,t0,tf,x0,v0,n)
      h=(tf-t0)/n;
      t=t0:h:tf;
%reserva memoria para n+1 element(i)os del vect(i)or x(i)
      x=zeros(n+1,1); 
      v=zeros(n+1,1);
      x(1)=x0; v(1)=v0;
      
      for i=1:n
        k1=h*v(i);
        l1=h*f(t(i),x(i),v(i));
        k2=h*(v(i)+l1/2);
        l2=h*f(t(i)+h/2,x(i)+k1/2,v(i)+l1/2);
        k3=h*(v(i)+l2/2);
        l3=h*f(t(i)+h/2,x(i)+k2/2,v(i)+l2/2);
        k4=h*(v(i)+l3);
        l4=h*f(t(i)+h,x(i)+k3,v(i)+l3);
        
        x(i+1)=x(i)+(k1+2*k2+2*k3+k4)/6;
        v(i+1)=v(i)+(l1+2*l2+2*l3+l4)/6;        
      end
end

La ecuación diferencial que describe un oscilador armónico amortiguado y su solución para unas condiciones iniciales fijadas es

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}+2\gamma \frac{dx}{dt}+{\omega }_0^{2}x=0\\ \omega =\sqrt{{\omega }_0^2-{\gamma }^2}\\ x=\exp (-\gamma t)\left(A\sin (\omega t)+B\cos (\omega t)\right)\\ v=\frac{dx}{dt}=-\gamma \exp (-\gamma t)\left(A\sin (\omega t)+B\cos (\omega t)\right)+\omega \exp (-\gamma t)\left(A\cos (\omega t)-B\sin (\omega t)\right)\end{array}}$

Condiciones iniciales: en el instante t=0, la posición inicial es x₀ y la velocidad inicial v₀.

${\displaystyle \begin{array}{l}t=0\{\begin{array}{l}{x}_0=B\\ v_0=-\gamma B+\omega A\end{array}\\ x=\exp (-\gamma t)\left(\frac{v_0+\gamma x_0}{\omega }\sin (\omega t)+x_0\cos (\omega t)\right)\end{array}}$

Escribimos un script en el que definiremos la función f(t,x,v), las condiciones iniciales y llamaremos a la función rk_2

w0=input('frecuencia angular w0: ');
g=input('rozamiento, gamma: ');
x0=input('posición inicial, x0: ');
v0=input('velocidad inicial,v0: ');
tf=input('tiempo final, tf: ');
n=input('número de pasos, n: ');
f=@(t,x,v) -2*g*v-w0*w0*x; 
%condiciones iniciales
t0=0;
hold on
%solución numérica
[t,x,v]=rk_2(f,t0,tf,x0,v0,n);
plot(t,x,'b')
%solución analítica
w=sqrt(w0*w0-g*g);
x=((v0+g*x0)*sin(w*t)/w+x0*cos(w*t)).*exp(-g*t);
plot(t,x,'r')
grid on
xlabel('t')
ylabel('x');
legend('aproximado','exacto')
title('oscilador amortiguado')
hold off

En la ventana de comandos corremos el script oscilador con distintas condiciones iniciales

>> oscilador
frecuencia angular, w0: 2
rozamiento, gamma: 0.5
posición inicial, x0: 1.5
velocidad inicial, v0: 0
tiempo final, tf: 8
número de pasos, n: 100

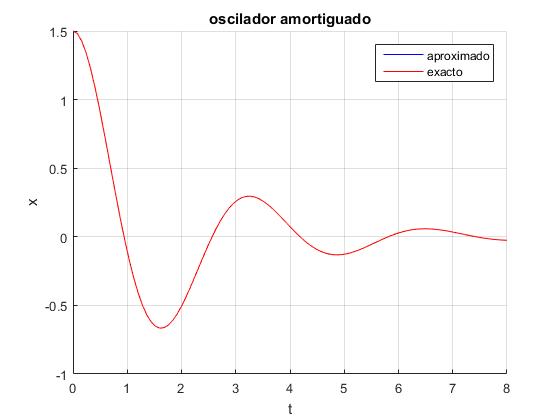
No se aprecia tampoco diferencia entre la solución exacta y la numérica, aplicando el procedimiento de Runge_Kutta.

Ejemplos en el Curso de Física

Ecuación de Lane-Emden. Interior de los cuerpos celestes

Referencias

Procedimiento de Picard

Numerical Solution of Ordinary Differential Equations