Método del punto medio

Este procedimiento se basa en el teorema de Bolzano que dice que si tenemos una función y=f(x), de variable real y continua en el intervalo [a, b], y el signo de la función en el extremo a es distinto al signo de la función en el extremo b del intervalo, existe al menos un valor c dentro de dicho intervalo tal que f(c)=0, c es por tanto, la raíz buscada, véase la figura.

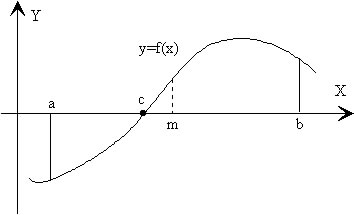
Supongamos una ecuación

f(x)=0

Para hallar la raíz de la función en el intervalo (a, b), se divide el intervalo en la mitad.

m=(a+b)/2

Pueden ocurrir uno de estos tres casos:

• Si f(m)=0 entonces m es la raíz buscada
• Si f(a) y f(m) tienen signos contrarios, como en la figura, la raíz buscada está en el intervalo (a, m).
• Si no se cumple la condición anterior, f(b) y f(m) tendrían signos contrarios y la raíz estaría en el intervalo (m, b).

El nuevo intervalo reducido se divide por la mitad y se procede de igual forma. Finalmente, en una cierta etapa del proceso tendremos bien la raíz exacta de la función f(x), o una secuencia de intervalos cada vez más reducidos [a₁,b₁], [a₂,b₂], .... [a_i, b_i]... tal que

${\displaystyle f(a_n)f(b_n)<0b_n-a_n=\frac{1}{2^n}(b-a)}$

Como los puntos extremos de la izquierda a₁, a₂, ... a_n, ...forman una sucesión creciente y acotada, y los de la derecha b₁, b₂, ... b_n, ... una sucesión acotada decreciente, existe un límite común que es la raíz ξ buscada.

${\displaystyle \xi =\underset{n\to \infty }{\lim }{a}_n=\underset{n\to \infty }{\lim }{b}_n}$

Si queremos conocer el valor de la raíz con un error menor que ε, tenemos que realizar un número n de iteracciones tal que

${\displaystyle n>\frac{1}{\ln 2}\ln \left(\frac{b-a}{\epsilon }\right)}$

Las condiciones de terminación del proceso

El ordenador trabaja con números de precisión limitada, por lo que tendremos que poner un criterio que establezca cuando la función f(x) se considera nula. Diremos que f(x) es nula cuando el valor absoluto de f(x) sea menor que una cantidad pequeña pero no nula ε₁.

${\displaystyle \left|f(x)\right|<{\epsilon }_1}$

En segundo lugar, no podemos programar un proceso indefinido, es preciso, que la rutina repetitiva acabe en un momento dado. El criterio empleado es el siguiente

${\displaystyle \left|\frac{a_n-b_n}{m}\right|<{\epsilon }_2}$

Siendo ε₂ cierta cantidad prefijada. La raíz se encuentra en el intervalo (a_n, b_n) y m es el punto medio, m=(a_n+b_n)/2 de dicho intervalo.

El tercer criterio de terminación establece, que el proceso de búsqueda de la raíz se interrumpirá después de un número prefijado de iteraciones, notificándose al usuario que no se ha encontrado la raíz de la función con las condiciones fijadas anteriormente.

Para poder codificar este procedimiento hemos de seguir los pasos siguientes

1. Partimos de un intervalo (a, b) en el que la función f(x) cambia de signo
2. Se calcula m, abscisa mitad del intervalo mediante m=(a+b)/2
3. Se verifican las condiciones de terminación
4. Si f(a) y f(m) tienen signos contrarios, como se ve en la figura, la raíz está en el intervalo (a, m), entonces b toma el valor de m.
5. Si la condición anterior no es cierta, la raíz se encuentra en el intervalo (m, b), por lo que a tomará el valor de m.
6. Se repite el proceso hasta que se cumple una u otra condición de terminación

function m=punto_medio(f, a, b, MAXITER)
    CERO=1e-10;
    ERROR=0.001;
    for i=1:MAXITER
        m=(a+b)/2;
        ym=f(m);
         if abs(ym)<CERO           
            break
         elseif abs((a-b)/m)<ERROR     
            break
         elseif (f(a)*ym)<0     
            b=m;
         else
            a=m;
         end
    end
    if(i==MAXITER) 
        error('no se ha encontrado la raiz')
    end
end

Resolvemos la ecuación trascendente f(x)=cos(x)-x=0, aplicando el procedimiento del punto medio.

En la gráfica, se representa y=cos(x)-x, tiene un cero y=0, para x comprendido entre 0.7 y 0.8

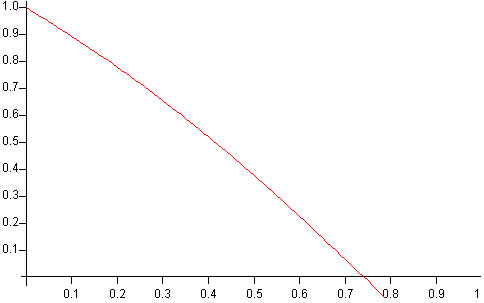
Definimos la función f para calcular la raíz de la ecuación trascendente y buscamos la raíz en el intervalo (0.5,1) haciendo 10 iteracciones. Vamos a la ventana de comandos

>> func=@(x) cos(x)-x;
>> punto_medio(func,0.5,1,10)
??? Error using ==> punto_medio at 18

Nos da un mensaje de error bien por que hemos puesto pocas iteracciones MAXITER, o por que no acotamos suficientemente el intervalo (a,b).

>> punto_medio(func,0.7,0.8,10)
ans =  0.7393

Raíces múltiples

La representación gráfica de la función, nos permitirá estimar los intervalos en los que la función cambia de signo y aplicar en consecuencia, el procedimiento mitad a cada intervalo. Si no es posible una representación gráfica, será preciso explorar el eje X en busca de intervalos en los que la función cambia de signo. Cuando los encontremos aplicaremos a cada uno de ellos el procedimiento del punto medio.

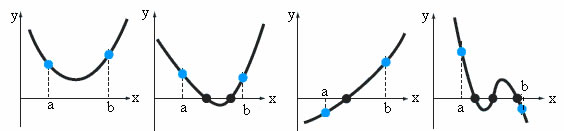
Esta exploración no es sencilla, ya que podemos encontrarnos con intervalos en que la función no cambia de signo ya sea por que no tiene raíces, o por que tiene un número par, tal como se ve en las figuras. La solución a este problema es hacer más pequeño el intervalo de exploración, esto implica más tiempo de cálculo y no garantiza que las raíces puedan ser encontradas si algunas de ellas están muy juntas, o la curva es tangente al eje X.

Las situaciones en las que nos podemos encontrar cuando buscamos las raíces de una función y=f(x) en un intervalo (a,b) se muestran en la figura

• f(a) y f(b) tienen el mismo signo, no hay raíz de la función en dicho intervalo, pero también puede ocurrir que haya un número par de raíces en dicho intervalo.
• f(a) y f(b) tienen distinto signo, hay una raíz de la función en dicho intervalo, pero también puede ocurrir que haya un número impar de raíces en dicho intervalo.

Vamos a crear un procedimiento que nos permita buscar los intervalos en los que la función cambia de signo y calcular la raíz en cada uno de ellos, definiendo una función denominada buscar_intervalos.

Se divide el intervalo (a,b) en n-1 intervalos igualmente espaciados (n divisiones incluidos los extremos) se calcula si en los extremos de los cada uno de los pequeños intervalos la función cambia de signo, en caso afirmativo se guardan los extremos (x_j, y_j) de dicho intervalo en una matriz xb. Si la matriz está vacía (no tiene ningún elemento) isempty, un mensaje nos lo indica. La función devuelve los intervalos (x_j, y_j) guardados en la matriz xb.

function xb = buscar_intervalos(f,a,b,n)
    x = linspace(a,b,n);
    j = 0; 
    xb=[];
    for i = 1:length(x)-1
        if sign(f(x(i))) ~= sign(f(x(i+1))) 
            j = j + 1;
            xb(j,1) = x(i);
            xb(j,2) = x(i+1);
        end
    end
    if isempty(xb) 
        disp('no se han encontrado cambios de signo')
    else
        disp(['número de intervalos:' int2str(j)]) 
    end
end

Este código es correcto, pero se puede hacer más eficiente, un asunto de vital importancia en el cálculo intensivo. Nos daremos cuenta, que se calcula dos veces la función f para el mismo valor de x, en el final de un intervalo y en el comienzo del siguiente, ahorraremos el tiempo que tarda al procesador en realizar estas operaciones si guardamos el valor de f(x) calculado al final del intervalo previo en la variable local y2 y lo asignamos a la variable y1, que guarda el valor de la función f(x) en el principio del intervalo siguiente.

function xb = buscar_intervalos(f,a,b,n)
    x = linspace(a,b,n);
    j = 0; 
    y1=f(x(1));
    xb=[];
   for i = 1:length(x)-1
        y2=f(x(i+1));
        if sign(y1) ~= sign(y2) 
            j = j + 1;
            xb(j,1) = x(i);
            xb(j,2) = x(i+1);
        end
        y1=y2;
    end
    if isempty(xb) 
        disp('no se han encontrado cambios de signo')
    else
        disp(['número de intervalos:' int2str(j)]) 
    end
end

Difracción Fraunhofer producida por una abertura circular

Al estudiar difracción Fraunhofer producida por una abertura circular, calculamos la intensidad en una dirección θ producida por una abertura circular de radio a es

${\displaystyle I=I_0{\left(\frac{2J_1(x)}{x}\right)}^{2}x=\frac{2\pi a}{\lambda }\sin \theta }$

Los mínimos de intensidad son los ceros de la función de Bessel J₁(x) cuya representación gráfica vemos en la figura

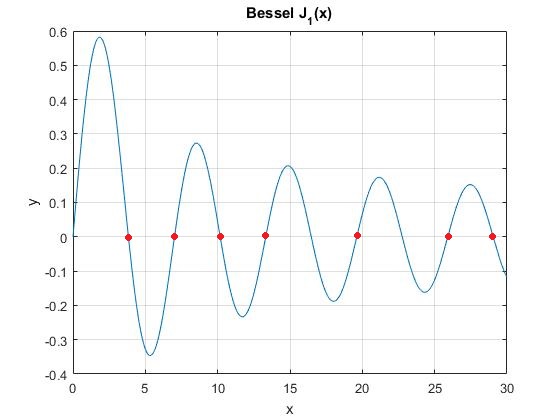
Si exploramos el intervalo comprendido entre a=0 y b=30, tomando 6 intervalos, de anchura dx=5 tal como vemos en la figura, la función cambia de signo en los intervalos (0,5), (5,10) y (20,25), pero no cambia de signo en los intervalos (10,15), (15,20) y (25,30) por tener un número par de raíces. Luego, si exploramos la función J₁(x) en el intervalo (0,30) tomando 6 intervalos de anchura dx=5 encontraremos solamente tres raíces de las nueve existentes.

Nota: omitimos el origen x=0, por que se produce un máximo (no un mínimo de intensidad)

${\displaystyle \underset{x\to 0}{\lim }\left(\frac{J_1(x)}{x}\right)=1}$

La función buscar_intervalos, busca los intervalos en los que la función J₁(x) cambia de signo, el intervalo en el que se explora la función es (0.1, 30), omitimos el origen. El número de divisiones del intervalo es 50, incluyendo los extremos. La función devuelve la matriz xb, que guarda los extremos (x_j, y_j) de cada intervalo en los que la función cambia de signo. La dimensión de la martriz xb nos la proporciona la función size y se guarda en el vector nb de dos elementos [filas, columnas]. El número de columnas nb(2) de la matriz es dos y el número de filas nb(1) es el número de intervalos.

Para cada intervalo en el que la función cambia de signo, se aplica el procedimiento del punto medio, llamando a la función punto_medio, para buscar la raíz en dicho intervalo.

Escribimos un script que realiza las siguientes tareas:

1. Define una función anónima besselj(1,x)
2. Utiliza la función buscar_intervalos para encontrar los intervalos en los que la función cambia de signo. Explorando el intervalo que va de a=0.1 y b=30. Se omite la primera raíz x=0 por que corresponde al máximo principal
3. Calcula e imprime las raíces empleando el procedimiento del punto medio, llamando a la función punto_medio. Alternativamente, se puede utilizar la función fzero de MATLAB

J1=@(x) besselj(1,x);
xb=buscar_intervalos(J1,0.1,30,50);
nb=size(xb);
min=zeros(nb(1),1);
disp('mínimos: difracción por abertura circular')
for i=1:nb(1)
    min(i)=punto_medio(J1,xb(i,1),xb(i,2),50);
    %min(i)=fzero(J1,[xb(i,1),xb(i,2)]);
end
disp(min)

En la ventana de comandos corremos el script para resolver la ecuación trascendente J₁(x)=0 en el intervalo (0.1,30)

mínimos: difracción por abertura circular
    3.8315
    7.0149
   10.1731
   13.3195
   16.4659
   19.6170
   22.7634
   25.9097
   29.0561

Difracción Fraunhofer producida por una rendija

Al estudiar la Difracción Fraunhofer producida por una rendija, vimos que el máximo principal ocurre en el origen x=0, y los máximos secundarios son las raíces de la ecuación trascendente

tan(x)-x=0

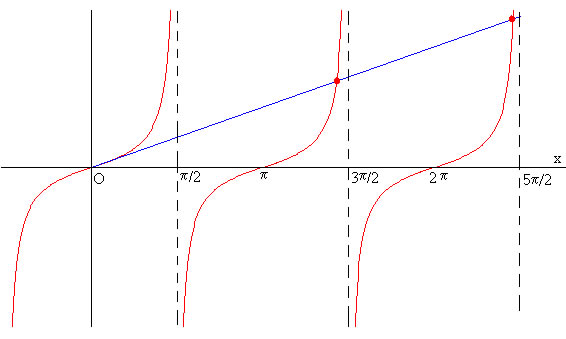
En la figura, se representan la recta y=x (color azul) y la función y=tan(x) (color rojo). Se ha hecho más pequeña la escala vertical que la horizontal.

Como observamos en la gráfica los máximos secundarios ocurren aproximadamente para x_n≈(2n+1)π/2 donde n=±1, ±2, ±3...

Escribimos un script que realiza las siguientes tareas:

1. Define una función anónima, tan(x)-x
2. Utiliza la función buscar_intervalos para encontrar los intervalos en los que la función cambia de signo. Explorando el intervalo que va de a=0.1 y b=7π/2. Se omite la primera raíz x=0 por que corresponde al máximo principal
3. Calcula e imprime las raíces empleando el procedimiento del punto medio, llamando a la función punto_medio. Alternativamente, se puede utilizar la función fzero de MATLAB

f=@(x) tan(x)-x;
xb=buscar_intervalos(f,0.1,7*pi/2,10);
nb=size(xb);
max=zeros(nb(1),1);
disp('máximos secundarios: difracción por una rendija')
for i=1:nb(1)
    max(i)=punto_medio(f,xb(i,1),xb(i,2),50);
    %max(i)=fzero(f,[xb(i,1),xb(i,2)]);
end
disp(max)

En la ventana de comandos corremos el script

máximos secundarios: difracción por una rendija
    1.5710 
    4.4933 
    4.7122  
   10.9018 

Como hemos visto en la figura (más arriba), la primera raíz es próxima a 3π/2=4.7124, la segunda, es próxima 5π/2=7.8540 y la tercera es próxima a 7π/2=10.9956. El resultado que hemos obtenido difiere notablemente. No parece adecuado el procedimiento del punto medio para calcular las raíces de la ecuación tan(x)-x=0. El problema radica, como se vé en la figura, en que la tangente se hace muy grande en valores próximos a x_n≈(2n+1)π/2.

Cambiamos la ecuación tan(x)-x=0 por su equivalente x·cos(x)-sin(x)=0. Representamos la función

y=x·cos(x)-sin(x)

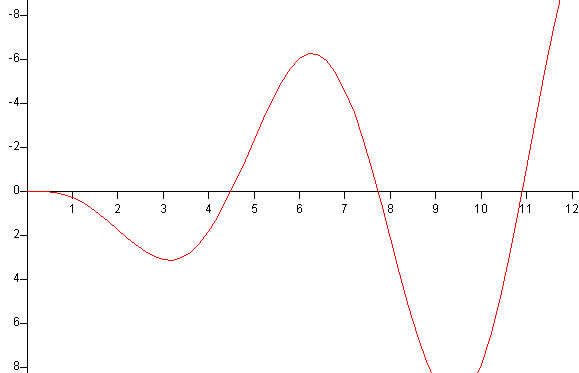
Escribimos otro script

f=@(x) x*cos(x)-sin(x);
xb=buscar_intervalos(f,0.1,7*pi/2,50);
nb=size(xb);
r=zeros(nb(1),1);
disp('máximos: difracción por una rendija')
for i=1:nb(1)
    r(i)=punto_medio(f,xb(i,1),xb(i,2),50)
    %r(i)=fzero(f,[xb(i,1),xb(i,2)]);
end
disp(r)

En la ventana de comandos

máximos: difracción por una rendija
    4.4934
    7.7253
   10.9041

Comparamos las raíces obtenidas con la representación gráfica y vemos que hemos obtenido un resultado mejor. Un procedimiento numérico no siempre es adecuado para resolver un problema particular.