Las integrales de Fresnel

Las integrales de Fresnel se definen

${\displaystyle \begin{array}{l}C(x)={\displaystyle \underset{0}{\overset{x}{\int }}\cos \left(\frac{\pi t^2}{2}\right)}dt\\ S(x)={\displaystyle \underset{0}{\overset{x}{\int }}\sin \left(\frac{\pi t^2}{2}\right)}dt\end{array}}$

La función fresnelc de MATLAB calcula la primera y fresnels, la segunda. Representamos ambas funciones

hold on
fplot(@(x) fresnelc(x), [-5,5])
fplot(@(x) fresnels(x), [-5,5])
hold off
grid on
xlabel('x')
legend('C(x)', 'S(x)','location','best')
ylabel('C(x), S(x)')
title('Las integrales de Fresnel')

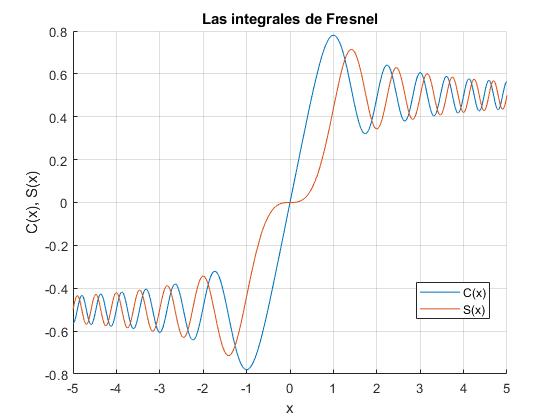
Cuando x se hace grande

>> fresnelc(inf)
ans =    0.5000
>> fresnels(inf)
ans =    0.5000

Las integrales de Fresnel tienden a 1/2

La espiral de Cornu

La espiral de Cornu, también conocida como clotoide, es una curva que se obtiene dando valores al parámetro x. A continuación, se unen los puntos cuya abscisa es C(x) y cuya ordenada es S(x).

fplot(@(x) fresnelc(x),@(x) fresnels(x), [0.02,7])
axis equal
grid on
xlabel('C(t)')
ylabel('S(t)')
title('La espiral de Cornu')

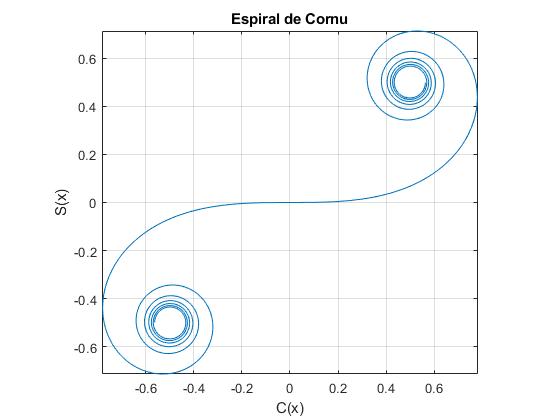
La espiral converge al centro de los dos remolinos (1/2, 1/2) y (-1/2, -1/2), a medida que x tiende a más infinito +∞ y menos infinito, -∞.

Curva de transición

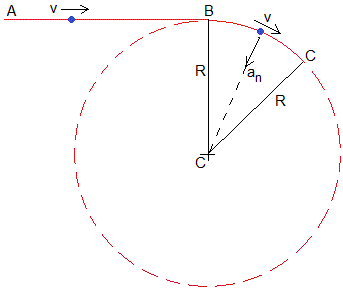
Un vehículo circula por una pista rectilínea AB con velocidad constante v y a continuación, por la pista circular BC de centro O y radio R. El vehículo experimenta una aceleración cuya dirección es radial y apuntando hacia el centro C, de módulo, a_n=v²/R

Desde el punto de vista de un observador no inercial situado en el vehículo, un pasajero experimenta una fuerza centrífuga, F_c=mv²/R.

La trayectoria rectilínea tiene una curvatura infinita (ρ=∞) y la trayectoria circular tiene una curvatura constante (ρ=R). El problema que se plantea en esta página es la de encontrar una curva (de transición) que una la trayectoria rectilínea y circular de modo que (1/ρ) se incremente de 0 a 1/R de forma constante.

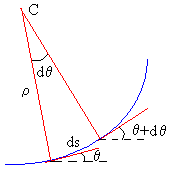
El radio de curvatura ρ y el centro C de curvatura se determinan del siguiente modo: Se traza la tangente a un punto de la trayectoria y a continuación, se traza la normal. Se toma un punto muy próximo al anterior, se traza la tangente y la normal en dicho punto.

Las normales se cortan en un punto denominado centro de curvatura C, y la distancia de C a uno u otro punto de la trayectoria, infinitamente próximos entre sí, se denomina radio de curvatura ρ.

Si el ángulo comprendido entre las dos tangentes es dθ, este es el ángulo que forman las dos normales. La longitud del arco entre los dos puntos considerados es ds=ρ·dθ.

${\displaystyle \frac{1}{\rho }=\frac{d\theta }{ds}}$

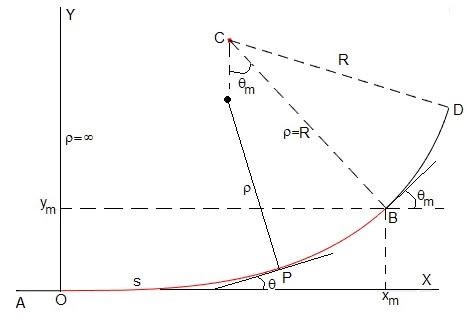
En la figura, la trayectoria rectilínea AO, se une a la trayectoria circular de centro C y radio R mediante la curva de transición OB (de color rojo). La longitud del arco OP es s. En P la tangente a la curva de transición forma un ángulo θ con la horizontal. El radio de curvatura en P es ρ. La longitud de la curva de transición OB es L, la tangente a la curva en B forma un ángulo θ_m con la horizontal y sus coordenadas son x_m e y_m

La curva de transición cumple que

${\displaystyle \frac{d}{ds}\left(\frac{1}{\rho }\right)=\frac{d^2\theta }{d{s}^2}=k}$

donde k es una constante. Integramos la ecuación diferencial

${\displaystyle \frac{d\theta }{ds}=\frac{1}{\rho }=ks+k_1}$

para s=0, 1/ρ=0, por lo que k₁=0

${\displaystyle \frac{1}{\rho }=ks,\rho s=\text{cte}}$

Una propiedad importante de la curva de transición es que el producto del arco s por el radio de curvatura ρ es constante a la largo de todos los puntos P de dicha trayectoria. Integramos de nuevo

${\displaystyle \theta =\frac{1}{2}k{s}^2+k_2}$

Para s=0, en O, la tangente a la curva de transición es horizontal, θ=0, luego, k₂=0.

${\displaystyle \theta =\frac{1}{2}k{s}^2}$

Para s=L, estamos en el punto B, final de la curva de transición y comienzo de la circular de radio ρ=R.

${\displaystyle \begin{array}{l}\frac{1}{R}=kL,k=\frac{1}{RL}\\ s=\sqrt{2RL\theta }\end{array}}$

La tangente a la trayectoria en B (s=L) forma un ángulo θ_m con la horizontal

${\displaystyle {\theta }_m=\frac{1}{2}\frac{1}{RL}{L}^2=\frac{L}{2R}}$

Ecuación de la curva de transición

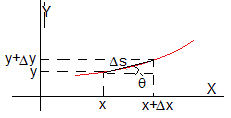
En el límite, cuando Δs→0, tiende a cero

${\displaystyle \begin{array}{l}\{\begin{array}{l}dx=\cos \theta ·ds\\ dy=\sin \theta ·ds\end{array}\\ ds=\sqrt{2RL}\frac{1}{2}\frac{d\theta }{\sqrt{\theta }}\end{array}}$

La curva buscada de transición, cuyas ecuaciones paramétricas son

${\displaystyle \begin{array}{l}x=\sqrt{\frac{RL}{2}}{\displaystyle \underset{0}{\overset{\theta }{\int }}\frac{\cos \theta }{\sqrt{\theta }}}d\theta \\ y=\sqrt{\frac{RL}{2}}{\displaystyle \underset{0}{\overset{\theta }{\int }}\frac{\sin \theta }{\sqrt{\theta }}}d\theta \end{array}}$

Haciendo el cambio de variable

${\displaystyle \begin{array}{l}\frac{\pi t^2}{2}=\theta \\ \pi t·dt=d\theta \end{array}}$

Obtenemos

${\displaystyle \begin{array}{l}x\left(\theta \right)=\sqrt{\pi RL}{\displaystyle \underset{0}{\overset{\sqrt{\frac{2\theta }{\pi }}}{\int }}\cos t^{2}dt}\\ y\left(\theta \right)=\sqrt{\pi RL}{\displaystyle \underset{0}{\overset{\sqrt{\frac{2\theta }{\pi }}}{\int }}\sin t^{2}dt}\end{array}}$

En términos de las integrales de Fresnel S(x) y C(x) se expresan

${\displaystyle \begin{array}{l}x=\sqrt{\pi RL}·S\left(\sqrt{\frac{2\theta }{\pi }}\right)\\ y=\sqrt{\pi RL}·C\left(\sqrt{\frac{2\theta }{\pi }}\right)\end{array}}$

Calculamos las coordenadas del punto B, cuya tangente forma un ángulo θ_m=L/(2R) con la horizontal.

${\displaystyle \begin{array}{l}{x}_m=\sqrt{\pi RL}·C\left(\sqrt{\frac{L}{\pi R}}\right)\\ y_m=\sqrt{\pi RL}·S\left(\sqrt{\frac{L}{\pi R}}\right)\end{array}}$

Las coordenadas del centro C del tramo circular de radio R son

${\displaystyle \{\begin{array}{l}{x}_C=x_m-R\sin {\theta }_m\\ y_C=y_m+R\cos {\theta }_m\end{array}}$

El código para representar los tramos de la curva: rectilíneo AO, transición, OB, circular, BD, es

R=1; %radio tramo circular
L=1.5; %longitud de la curva de transición
x_m=sqrt(pi*R*L)*fresnelc(sqrt(L/(pi*R))); %extremo
y_m=sqrt(pi*R*L)*fresnels(sqrt(L/(pi*R)));
x_C=x_m-R*sin(L/(2*R)); %centro C
y_C=y_m+R*cos(L/(2*R));
phi=L/(2*R)+pi/6; %ángulo del tramo circular
hold on
line([-0.2,0],[0,0],'color','k')
plot(x_C,y_C,'ro','markersize',3,'markerfacecolor','r')
fplot(@(t) sqrt(pi*R*L)*fresnelc(sqrt(2*t/pi)),@(t) sqrt(pi*R*L)*
fresnels(sqrt(2*t/pi)),[0,L/(2*R)],'color','r');
fplot(@(t) x_C+R*sin(t), @(t) y_C-R*cos(t),[L/(2*R), phi],'color','k')
line([x_C,x_m],[y_C,y_m],'lineStyle','--','color','k')
line([x_C,x_C+R*sin(phi)],[y_C,y_C-R*cos(phi)],'lineStyle','--','color','k')
hold off
axis equal

Aceleraciones

Supongamos que el vehículo circula por la vía con velocidad v constante

• En el tramo recto AO, la aceleración a_n=0

• En el tramo circular de centro C y radio R, la aceleración es $a_n=\frac{v^2}{R}$

• En la curva de transición OB, $a_n=\frac{v^2}{\rho }=\frac{v^2}{RL}s$, que se incrementa linealmente de 0 a v²/R

Curva compuesta

Unimos los tramos rectos AO y BO que forman un ángulo π-φ mediante un arco de circunferencia de centro C radio R.

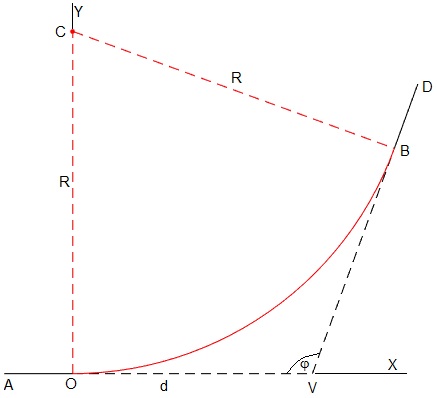
El código para representar los tramos de la curva es

R=1; %radio del tramo circular
phi=110*pi/180; %ángulo de las tramos rectilíneos
d=R/tan(phi/2); %distancia al vértice V
hold on
line([-0.2,0],[0,0],'color','k')
line([0,d],[0,0],'lineStyle','--','color','k')
line([d,d-d*cos(phi)],[0, d*sin(phi)],'lineStyle','--','color','k')
line([d-d*cos(phi), d-(d+0.2)*cos(phi)], [d*sin(phi),(d+0.2)*sin(phi)],
'color','k')
plot(0, R,'ro','markersize',3,'markerfacecolor','r')
fplot(@(t) R*sin(t),@(t) R-R*cos(t),[0,pi-phi],'color','r')
line([0,0],[0,R],'lineStyle','--','color','r')
line([0,R*sin(pi-phi)],[R,R-R*cos(pi-phi)],'lineStyle','--','color','r')
hold off
axis off
axis equal

Para evitar los cambios bruscos de aceleración, como hemos visto en el apartado anterior, entre los tramos rectos y el arco de circunferencia de radio R insertaremos dos curvas de transición de longitud L

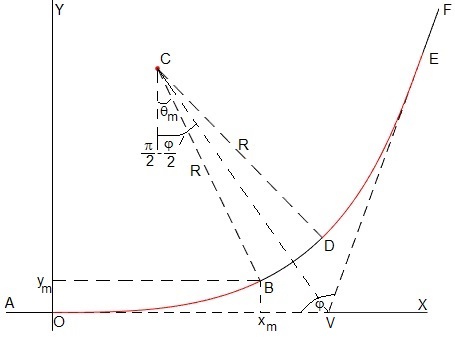
La trayectoria AO (rectilínea), OB (transición), BD (circular), DE (transición), EF (rectilínea), es simétrica respecto de la bisetriz VC

Como en el apartado anterior

${\displaystyle \begin{array}{l}\{\begin{array}{l}{x}_m=\sqrt{\pi RL}·C\left(\sqrt{\frac{L}{\pi R}}\right)\\ y_m=\sqrt{\pi RL}·S\left(\sqrt{\frac{L}{\pi R}}\right)\end{array}\\ {\theta }_m=\frac{L}{2R}\end{array}}$

x_m e y_m son las coordenadas del punto B, final de la curva de transición y principio de la circular de radio R y centro C. θ_m es el ángulo que forma la tangente a la curva en B con la horizontal.

Las coordenadas del centro de la circunferencia C son

${\displaystyle \{\begin{array}{l}{x}_C=x_m-R\sin {\theta }_m\\ y_C=y_m+R\cos {\theta }_m\end{array}}$

En esta figura, superponemos la trayectoria circular GH que une los tramos recilíneos AG y HF (en color azul), y la trayectoria que evita los cambios bruscos de aceleración, AO (rectilínea), OB (transición), BD (circular), DE (transición), EF (rectilínea)

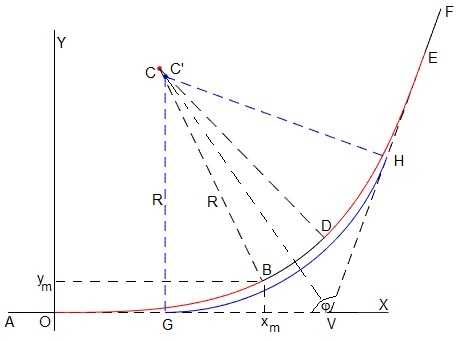
Los centros de los tramos circulares C (del tramo BC) y C' (del tramo GH) están desplazados a lo largo de la bisetriz VC. Ampliamos la figura

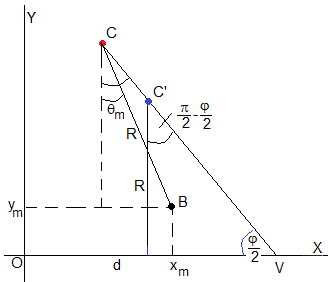
Las distancias CV y C'V, son

${\displaystyle C\text{'}V=\frac{R}{\sin \frac{\phi }{2}},CV=\frac{y_m+R\cos {\theta }_m}{\sin \frac{\phi }{2}}}$

La distancia d de O a V es

${\displaystyle \begin{array}{l}d=x_m-R\sin {\theta }_m+CV·\cos \frac{\phi }{2}=\\ x_m-R\sin {\theta }_m+\frac{y_m+R\cos {\theta }_m}{\tan \frac{\phi }{2}}\end{array}}$

Las coordenadas del centro C' son

${\displaystyle \begin{array}{l}{x}_{C\text{'}}=x_C+CC\text{'}\sin \left(\frac{\pi }{2}-\frac{\phi }{2}\right)=x_m-R\sin {\theta }_m+\left(CV-C\text{'}V\right)\cos \frac{\phi }{2}\\ \{\begin{array}{l}{x}_{C\text{'}}=x_m-R\sin {\theta }_m+\frac{y_m+R\cos {\theta }_m-R}{\tan \frac{\phi }{2}}\\ y_{C\text{'}}=R\end{array}\end{array}}$

Simetría

Como apreciamos en la figura, la trayectoria es simétrica respecto de la bisetriz VC

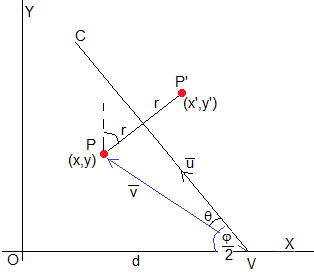
Calculamos las coordenadas del punto P' (x', y') simétrico de P (x, y) respecto a la bisetriz VC.

${\displaystyle \{\begin{array}{l}x\text{'}=x+2r\sin \frac{\phi }{2}\\ y\text{'}=y+2r\cos \frac{\phi }{2}\end{array}}$

Siendo r la distancia del punto P (x, y) a la recta de pendiente tan(π-φ/2) y que pasa por el punto (d,0), cuya ecuación es

${\displaystyle y=\tan \left(\pi -\frac{\phi }{2}\right)(x-d)}$

Utilizamos el módulo del producto vectorial, para calcular la distancia r del punto P a la recta.

${\displaystyle r=v\sin \theta =\frac{\left|\overrightarrow{u}\times \overrightarrow{v}\right|}{u}=\frac{\left|u_x{v}_y-u_y{v}_x\right|}{u}}$

• El vector $\overrightarrow{v}$, une el punto P(x,y) con el vértice V (d, 0),
• El vector $\overrightarrow{u}$, une cualquier punto de la recta (x, tan(π-φ/2)(x-d)) con el vértice V (d,0)

La distancia r del punto P a la recta es

${\displaystyle \begin{array}{l}\{\begin{array}{l}\overrightarrow{v}=(x-d)\widehat{i}+y\widehat{j}\\ \overrightarrow{u}=\widehat{i}+\tan \left(\pi -\frac{\phi }{2}\right)\widehat{j}\end{array}\\ r=\frac{\left|\tan \left(\pi -\frac{\phi }{2}\right)(x-d)-y\right|}{\sqrt{1+{\tan }^2\left(\pi -\frac{\phi }{2}\right)}}=\left|y+(d-x)\tan \left(\pi -\frac{\phi }{2}\right)\right|\cos \left(\pi -\frac{\phi }{2}\right)=\\ \left|y\cos \left(\pi -\frac{\phi }{2}\right)+(d-x)\sin \left(\pi -\frac{\phi }{2}\right)\right|\end{array}}$

La transformación que relaciona (x', y') con (x, y) nos permite representar la curva de transición simétrica.

El código para representar los tramos de la curva es

R=1; %radio del tramo circular
phi=110*pi/180; %ángulo de las tramos rectilíneos
L=0.9; %longitud de la curva de transición
x_m=sqrt(pi*R*L)*fresnelc(sqrt(L/(pi*R)));
y_m=sqrt(pi*R*L)*fresnels(sqrt(L/(pi*R)));
d=x_m-R*sin(L/(2*R))+(y_m+R*cos(L/(2*R)))/tan(phi/2);
x_C=x_m-R*sin(L/(2*R));
y_C=y_m+R*cos(L/(2*R));
hold on
line([-0.2,0],[0,0],'color','k')
line([0,d],[0,0],'lineStyle','--','color','k')
line([d,d-d*cos(phi)],[0, d*sin(phi)],'lineStyle','--','color','k')
line([d-d*cos(phi), d-(d+0.2)*cos(phi)], [d*sin(phi),(d+0.2)*sin(phi)],
'color','k')
plot(x_C,y_C,'ro','markersize',3,'markerfacecolor','r')
delta=pi-phi-L/R;
fplot(@(t) x_C+R*sin(t), @(t) y_C-R*cos(t),[pi/2-phi/2-delta/2, 
pi/2-phi/2+delta/2],'color','k')
line([x_C, x_C+R*sin(pi/2-phi/2-delta/2)],[y_C,y_C-R*cos(pi/2-phi/2-delta/2)],
'lineStyle','--','color','k')
line([x_C, x_C+R*sin(pi/2-phi/2+delta/2)],[y_C,y_C-R*cos(pi/2-phi/2+delta/2)],
'lineStyle','--','color','k')
th=linspace(0, L/(2*R),50);
x=sqrt(pi*R*L)*fresnelc(sqrt(2*th/pi));
y=sqrt(pi*R*L)*fresnels(sqrt(2*th/pi));
plot(x,y,'r')
dd=abs(y*cos(pi-phi/2)+(d-x)*sin(pi-phi/2));
xx=x+2*dd*sin(phi/2);
yy=y+2*dd*cos(phi/2);
plot(xx,yy,'r')
%tramo circular de centro C'
x_Cp=x_C+(y_m+R*cos(L/(2*R))-R)/tan(phi/2);
y_Cp=R;
plot(x_Cp, y_Cp,'bo','markersize',3,'markerfacecolor','b')
fplot(@(t) x_Cp+R*sin(t),@(t) y_Cp-R*cos(t),[0, pi-phi],'color','b')
line([x_Cp,x_Cp],[y_Cp,y_Cp-R],'lineStyle','--','color','b')
line([x_Cp,x_Cp+R*sin(pi-phi)],[y_Cp,y_Cp-R*cos(pi-phi)],'lineStyle',
'--','color','b')
hold off
axis equal

Curva de transición que une dos trayectorias circulares

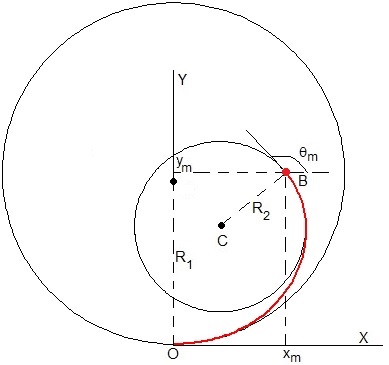
Sean dos trayectorias circulares de radio R₁ y R₂. Situamos la primera centrada en el eje Y a la altura R₁.

La curva de transición cumple que

${\displaystyle \frac{d}{ds}\left(\frac{1}{\rho }\right)=\frac{d^2\theta }{d{s}^2}=k}$

donde k es una constante. Integramos la ecuación diferencial

${\displaystyle \frac{d\theta }{ds}=\frac{1}{\rho }=ks+k_1}$

para s=0, 1/ρ=1/R₁, y para s=L, 1/ρ=1/R₂, despejamos las constantes k y k₁

${\displaystyle \frac{d\theta }{ds}=\frac{1}{\rho }=\left(\frac{1}{R_2}-\frac{1}{R_1}\right)\frac{s}{L}+\frac{1}{R_1}}$

Integramos de nuevo

${\displaystyle \theta =\frac{1}{2}\frac{R_1-R_2}{R_1{R}_{2}L}{s}^2+\frac{1}{R_1}s+k_2}$

Para s=0, en O, la tangente a la curva de transición es horizontal, θ=0, luego, k₂=0.

${\displaystyle \theta =\frac{1}{2}\frac{R_1-R_2}{R_1{R}_{2}L}{s}^2+\frac{1}{R_1}s}$

La tangente a la trayectoria en B (s=L) forma un ángulo θ_m con la horizontal

${\displaystyle {\theta }_m=\frac{1}{2}\frac{R_1+R_2}{R_1{R}_2}L}$

Ecuación de la curva de transición

La curva buscada de transición, cuyas ecuaciones paramétricas son

${\displaystyle \{\begin{array}{l}x={\displaystyle \underset{0}{\overset{s}{\int }}\cos \theta ·ds}={\displaystyle \underset{0}{\overset{s}{\int }}\cos \left(\frac{1}{2}\frac{R_1-R_2}{R_1{R}_{2}L}{s}^2+\frac{1}{R_1}s\right)·ds}\\ y={\displaystyle \underset{0}{\overset{s}{\int }}\sin \theta ·ds}={\displaystyle \underset{0}{\overset{s}{\int }}\sin \left(\frac{1}{2}\frac{R_1-R_2}{R_1{R}_{2}L}{s}^2+\frac{1}{R_1}s\right)·ds}\end{array}}$

Calculamos las coordenadas del punto B, cuya tangente forma un ángulo θ_m con la horizontal.

${\displaystyle \{\begin{array}{l}{x}_m={\displaystyle \underset{0}{\overset{L}{\int }}\cos \left(\frac{1}{2}\frac{R_1-R_2}{R_1{R}_{2}L}{s}^2+\frac{1}{R_1}s\right)·ds}\\ y_m={\displaystyle \underset{0}{\overset{L}{\int }}\sin \left(\frac{1}{2}\frac{R_1-R_2}{R_1{R}_{2}L}{s}^2+\frac{1}{R_1}s\right)·ds}\end{array}}$

Calculamos estas integrales utilizando el procedimiento numérico integral de MATLAB

Las coordenadas del centro C de la trayectoria circular de radio R₂ son

${\displaystyle \{\begin{array}{l}{x}_C=x_m-R_2\sin {\theta }_m\\ y_C=y_m+R_2\cos {\theta }_m\end{array}}$

El código para representar los tramos de la curva: circular de radio R₁=1, transición, OB, (línea de gruesa de color rojo), circular de radio R₂=0.5, es

R1=1; %radio tramo circular
R2=0.5;
L=1.5; %longitud de la curva de transición
k=(R1-R2)/(2*L*R1*R2);
th_m=(R1+R2)*L/(2*R1*R2);
x_m=integral(@(x) cos(x/R1+k*x.^2),0,L); %extremo
y_m=integral(@(x) sin(x/R1+k*x.^2),0,L); 
x_C=x_m-R2*sin(th_m); %centro C
y_C=y_m+R2*cos(th_m);
hold on
plot(x_C,y_C,'ro','markersize',3,'markerfacecolor','r')
plot(0,R1,'ro','markersize',3,'markerfacecolor','r')
fplot(@(t) R1*cos(t), @(t) R1-R1*sin(t), [0,2*pi],'color','k')
fplot(@(t) x_C+R2*cos(t), @(t) y_C+R2*sin(t), [0,2*pi],'color','k')
line([x_C,x_m],[y_C,y_m],'lineStyle','--','color','k')
line([0,0],[0,R1],'lineStyle','--','color','k')
%curva de transición
xx=linspace(0,L,100);
xs=zeros(1,length(xx));
ys=zeros(1,length(xx));
i=1;
for x=xx
    xs(i)=integral(@(x) cos(x/R1+k*x.^2),0,x);
    ys(i)=integral(@(x) sin(x/R1+k*x.^2),0,x);
    i=i+1;
end
plot(xs,ys, 'lineWidth',1.2,'color','r')
hold off
axis equal

Cuando R₁=R₂, las dos circunfencias coinciden y la curva de trasnsición es un arco de circunferencia de longitud L

${\displaystyle \{\begin{array}{l}x=R_1\sin \left(\frac{s}{R_1}\right)\\ y=R_1-R_1\cos \left(\frac{s}{R_1}\right)\end{array}}$

Otros ejemplos en el Curso de Física

Movimiento de un disco impulsado por una fuerza de módulo constante

Difracción Fresnel producida por una abertura rectangular

Difracción de Fresnel

Referencias

R. E. Deakin. ENGINEERING SURVEYING 1. HORIZONTAL CURVES.