El péndulo doble

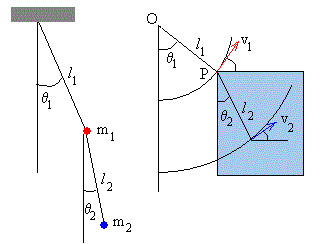
El péndulo doble como se muestra en la figura, está formado por dos péndulos simples de longitudes l₁ y l₂, de los que cuelgan partículas de masas m₁ y m₂. En un instante determinado t, los hilos inextensibles forman ángulos θ₁ y θ₂ con la vertical.

Energía

La energía del sistema es la suma de la energía potencial y de la energía cinética de las dos partículas.

Energía potencial

Situamos el nivel cero de energía potencial en el punto de suspensión del primer péndulo. La energía potencial es

V=-m₁·gl₁cos θ₁-m₂g(l₁cos θ₁+l₂cos θ₂)=-(m₁+m₂)·gl₁cos θ₁-m₂gl₂cos θ₂

Energía cinética

El módulo de la velocidad del primer péndulo es v₁=l₁·dθ₁/dt (velocidad angular por el radio de la circunferencia que describe), sus componentes son

$\vec{v_{1}} = l_{1} \frac{d θ_{1}}{d t} \cos θ_{1} \hat{i} + l_{1} \frac{d θ_{1}}{d t} \sin θ_{1} \hat{j}$

El módulo de la velocidad de la segunda partícula en un sistema de referencia que se mueve con la velocidad $\vec{v_{1}}$ de la primera partícula es v₂=l₂·dθ₂/dt. Sus componentes son

$\vec{v_{2}} = l_{2} \frac{d θ_{2}}{d t} \cos θ_{2} \hat{i} + l_{2} \frac{d θ_{2}}{d t} \sin θ_{2} \hat{j}$

La velocidad de la segunda partícula respecto al sistema de referencia inercial situado en O es la suma vectorial de ambas velocidades (véase la figura de la derecha)

$\vec{v_{2}} + \vec{v_{1}} = (l_{2} \frac{d θ_{2}}{d t} \cos θ_{2} + l_{1} \frac{d θ_{1}}{d t} \cos θ_{1}) \hat{i} + (l_{2} \frac{d θ_{2}}{d t} \sin θ_{2} + l_{1} \frac{d θ_{1}}{d t} \sin θ_{1}) \hat{j}$

Calculamos los módulos de las velocidades de las dos partículas. La energía cinética del sistema es

$T = \frac{1}{2} m_{1} l_{1}^{2} {(\frac{d θ_{1}}{d t})}^{2} + \frac{1}{2} m_{2} l_{1}^{2} {(\frac{d θ_{1}}{d t})}^{2} + \frac{1}{2} m_{2} l_{2}^{2} {(\frac{d θ_{2}}{d t})}^{2} + m_{2} l_{1} l_{2} (\frac{d θ_{1}}{d t}) (\frac{d θ_{2}}{d t}) \cos (θ_{1} - θ_{2})$

Ecuaciones del movimiento

Las ecuaciones del movimiento de Lagrange nos llevan al sistema de dos ecuaciones diferenciales de segundo orden.La lagrangiana L=T-V

$\begin{array}{l} L = \frac{1}{2} (m_{1} + m_{2}) l_{1}^{2} {(\frac{d θ_{1}}{d t})}^{2} + \frac{1}{2} m_{2} l_{2}^{2} {(\frac{d θ_{2}}{d t})}^{2} + m_{2} l_{1} l_{2} (\frac{d θ_{1}}{d t}) (\frac{d θ_{2}}{d t}) \cos (θ_{1} - θ_{2}) \\ + (m_{1} + m_{2}) g l_{1} \cos θ_{1} + m_{2} g l_{2} \cos θ_{2} \end{array}$

Las primera ecuación del movimiento se obtiene

$\begin{array}{l} \frac{d}{d t} \frac{\partial L}{\partial {\dot{θ}}_{1}} - \frac{\partial L}{\partial θ_{1}} = 0 {\dot{θ}}_{1} = \frac{d θ_{1}}{d t} \\ \frac{\partial L}{\partial {\dot{θ}}_{1}} = (m_{1} + m_{2}) l_{1}^{2} (\frac{d θ_{1}}{d t}) + m_{2} l_{1} l_{2} (\frac{d θ_{2}}{d t}) \cos (θ_{1} - θ_{2}) \\ \frac{\partial L}{\partial θ_{1}} = - m_{2} l_{1} l_{2} (\frac{d θ_{1}}{d t}) (\frac{d θ_{2}}{d t}) \sin (θ_{1} - θ_{2}) - (m_{1} + m_{2}) g l_{1} \sin θ_{1} \\ \frac{d}{d t} (\frac{\partial L}{\partial {\dot{θ}}_{1}}) = (m_{1} + m_{2}) l_{1}^{2} (\frac{d^{2} θ_{1}}{d t^{2}}) + m_{2} l_{1} l_{2} (\frac{d^{2} θ_{2}}{d t^{2}}) \cos (θ_{1} - θ_{2}) - m_{2} l_{1} l_{2} (\frac{d θ_{2}}{d t}) \sin (θ_{1} - θ_{2}) (\frac{d θ_{1}}{d t} + \frac{d θ_{2}}{d t}) \\ (m_{1} + m_{2}) l_{1}^{2} (\frac{d^{2} θ_{1}}{d t^{2}}) + m_{2} l_{1} l_{2} (\frac{d^{2} θ_{2}}{d t^{2}}) \cos (θ_{1} - θ_{2}) + m_{2} l_{1} l_{2} {(\frac{d θ_{2}}{d t})}^{2} \sin (θ_{1} - θ_{2}) + (m_{1} + m_{2}) g l_{1} \sin θ_{1} = 0 \end{array}$

La segunda ecuación del movimiento, se obtiene

$\begin{array}{l} \frac{d}{d t} \frac{\partial L}{\partial {\dot{θ}}_{2}} - \frac{\partial L}{\partial θ_{2}} = 0 {\dot{θ}}_{2} = \frac{d θ_{2}}{d t} \\ \frac{\partial L}{\partial {\dot{θ}}_{2}} = m_{2} l_{2}^{2} (\frac{d θ_{2}}{d t}) + m_{2} l_{1} l_{2} (\frac{d θ_{1}}{d t}) \cos (θ_{1} - θ_{2}) \\ \frac{\partial L}{\partial θ_{1}} = - m_{2} l_{1} l_{2} (\frac{d θ_{1}}{d t}) (\frac{d θ_{2}}{d t}) \sin (θ_{1} - θ_{2}) - m_{2} g l_{2} \sin θ_{2} \\ \frac{d}{d t} (\frac{\partial L}{\partial {\dot{θ}}_{1}}) = m_{2} l_{2}^{2} (\frac{d^{2} θ_{2}}{d t^{2}}) + m_{2} l_{1} l_{2} (\frac{d^{2} θ_{1}}{d t^{2}}) \cos (θ_{1} - θ_{2}) - m_{2} l_{1} l_{2} (\frac{d θ_{1}}{d t}) \sin (θ_{1} - θ_{2}) (\frac{d θ_{1}}{d t} + \frac{d θ_{2}}{d t}) \\ m_{2} l_{2}^{2} (\frac{d^{2} θ_{2}}{d t^{2}}) + m_{2} l_{1} l_{2} (\frac{d^{2} θ_{1}}{d t^{2}}) \cos (θ_{1} - θ_{2}) - m_{2} l_{1} l_{2} {(\frac{d θ_{1}}{d t})}^{2} \sin (θ_{1} - θ_{2}) + m_{2} g l_{2} \sin θ_{2} = 0 \end{array}$

Dividimos ambas ecuaciones por m₂l₁l₂ y llamamos m=m₁/m₂

$\begin{array}{l} (m + 1) \frac{l_{1}}{l_{2}} (\frac{d^{2} θ_{1}}{d t^{2}}) + (\frac{d^{2} θ_{2}}{d t^{2}}) \cos (θ_{1} - θ_{2}) + {(\frac{d θ_{2}}{d t})}^{2} \sin (θ_{1} - θ_{2}) + (m + 1) \frac{g}{l_{2}} \sin θ_{1} = 0 \\ \frac{l_{2}}{l_{1}} (\frac{d^{2} θ_{2}}{d t^{2}}) + (\frac{d^{2} θ_{1}}{d t^{2}}) \cos (θ_{1} - θ_{2}) - {(\frac{d θ_{1}}{d t})}^{2} \sin (θ_{1} - θ_{2}) + \frac{g}{l_{1}} \sin θ_{2} = 0 \end{array}$

Tenemos un sistema de dos ecuaciones con dos incógnitas en las que tenemos que despejar la derivada segunda de la posición angular de θ₁ y θ₂ de cada uno de los péndulos para proceder a su integración numérica.

$\begin{array}{l} {\begin{cases} a_{1} \frac{d^{2} θ_{1}}{d t^{2}} + b \frac{d^{2} θ_{2}}{d t^{2}} + c_{1} = 0 \\ a_{2} \frac{d^{2} θ_{2}}{d t^{2}} + b \frac{d^{2} θ_{1}}{d t^{2}} + c_{2} = 0 \end{cases} \\ \frac{d^{2} θ_{1}}{d t^{2}} = \frac{a_{2} c_{1} - b c_{2}}{b^{2} - a_{1} a_{2}} \\ \frac{d^{2} θ_{2}}{d t^{2}} = \frac{a_{1} c_{2} - b c_{1}}{b^{2} - a_{1} a_{2}} \end{array}$

El resultado es

$\begin{array}{l} \frac{d^{2} θ_{1}}{d t^{2}} = \frac{\cos (θ_{1} - θ_{2}) (\frac{g}{l_{1}} \sin θ_{2} - {(\frac{d θ_{1}}{d t})}^{2} \sin (θ_{1} - θ_{2})) - \frac{l_{2}}{l_{1}} ((m + 1) \frac{g}{l_{2}} \sin θ_{1} + {(\frac{d θ_{2}}{d t})}^{2} \sin (θ_{1} - θ_{2}))}{m + \sin^{2} (θ_{1} - θ_{2})} \\ \frac{d^{2} θ_{2}}{d t^{2}} = \frac{\cos (θ_{1} - θ_{2}) ((m + 1) \frac{g}{l_{2}} \sin θ_{1} + {(\frac{d θ_{2}}{d t})}^{2} \sin (θ_{1} - θ_{2})) - (m + 1) \frac{l_{1}}{l_{2}} (\frac{g}{l_{1}} \sin θ_{2} - {(\frac{d θ_{1}}{d t})}^{2} \sin (θ_{1} - θ_{2}))}{m + \sin^{2} (θ_{1} - θ_{2})} \end{array}$

Se resuelve el sistema de ecuaciones diferenciales por procedimientos numéricos con las siguientes condiciones iniciales: en el instante t=0, θ₁=θ₁₀ y dθ₁/dt=0, θ₂=θ₂₀ y dθ₂/dt=0

La energía total del sistema de dos partículas es constante, lo que nos permitirá verificar si el procedimiento numérico aplicado da buenos resultados

$\begin{array}{l} E = \frac{1}{2} (m_{1} + m_{2}) l_{1}^{2} {(\frac{d θ_{1}}{d t})}^{2} + \frac{1}{2} m_{2} l_{2}^{2} {(\frac{d θ_{2}}{d t})}^{2} + m_{2} l_{1} l_{2} (\frac{d θ_{1}}{d t}) (\frac{d θ_{2}}{d t}) \cos (θ_{1} - θ_{2}) \\ - (m_{1} + m_{2}) g l_{1} \cos θ_{1} - m_{2} g l_{2} \cos θ_{2} \end{array}$

m=1;  %relación m1/m2
L1=1;
L2=2;
x0=[pi/3, 0, -pi/6, 0];
tspan=[0,10];

fg=@(t,x)[x(2);(cos(x(1)-x(3))*(9.8*sin(x(3))/L1-x(2)^2*sin(x(1)-x(3)))-
(L2*((m+1)*9.8*sin(x(1))/L2+x(4)^2*sin(x(1)-x(3)))/L1))
/(m+sin(x(1)-x(3))*sin(x(1)-x(3))); x(4);
(cos(x(1)-x(3))*((m+1)*9.8*sin(x(1))/L2+x(4)^2*sin(x(1)-x(3)))
-((m+1)*L1*(9.8*sin(x(3))
/L1-x(2)^2*sin(x(1)-x(3)))/L2))/(m+sin(x(1)-x(3))*sin(x(1)-x(3)))];
[t,x]=ode45(fg,tspan,x0);
hold on
plot(x(:,1),x(:,2),'r') 
plot(x(:,3),x(:,4),'b')
hold off
grid on
legend('1','2');
xlabel('\theta_1, \theta_2')
ylabel('\omega_1, \omega_2')
title('Péndulo doble')

Einicial=-(m+1)*9.8*cos(x0(1))/L2-9.8*cos(x0(3))/L1;
E=(m+1)*L1*x(:,2).^2/(2*L2)+L2*x(:,4).^2/(2*L1)+(x(:,2).*x(:,4)).
*cos(x(:,1)-x(:,3))-(m+1)*9.8*cos(x(:,1))/L2-9.8*cos(x(:,3))/L1;
max(abs(100*(Einicial-E)/Einicial)) 
%error máximo en el intervalo de tiempo especificado

ans =    0.7792

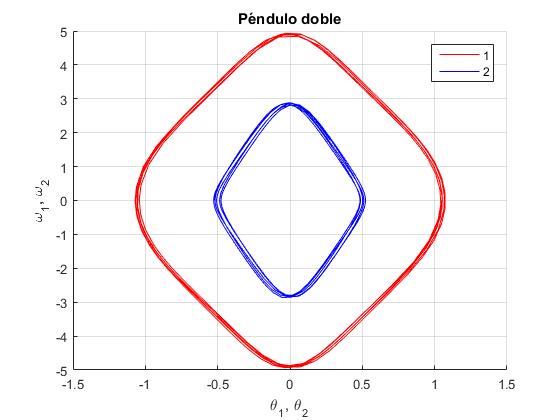
Representación de la trayectoria de las dos partículas en el espacio de las fases: θ₁, dθ₁/dt en color rojo y θ₂, dθ₂/dt en color azul

Actividades

Se introduce

La masa m₂ de la partícula del péndulo inferior en kg, en el control titulado Masa 2.
La masa de la partícula del péndulo superior se ha fijado en m₁=1 kg
La longitud l₂ del péndulo inferior en el control titulado Longitud 2.
La longitud del péndulo superior se ha fijado en l₁=1 m
El ángulo de desviación inicial θ₁₀ del péndulo superior en grados, en el control titulado Angulo 1.
El ángulo de desviación inicial θ₂₀ del péndulo inferior en grados, en el control titulado Angulo 2.

Se pulsa el botón titulado Nuevo

Se observa el movimiento de los dos partículas en el espacio de las fases: θ₁, dθ₁/dt en color rojo y θ₂, dθ₂/dt en color azul.

Se calcula el tanto por ciento de error,

$| \frac{E - E_{0}}{E_{0}} | \cdot 100$ .

Donde E₀=-(m₁+m₂)·gl₁cos θ₁₀-m₂gl₂cos θ₂₀, es la energía inicial y E es la energía en el instante t. Ambas cantidades deberían ser iguales. Cuando el tanto por ciento de error supera el 1%, el proceso de integración se detiene, se considera el procedimiento numérico no resuelve adecuadamente el sistema de ecuaciones diferenciales y se invita al lector a disminuir el Paso de integración, que por defecto, se ha establecido en h=0.01

Se puede controlar la trayectoria en el control titulado Trayectoria, n. puntos. Se dibuja un punto por cada paso de integración de la ecuación diferencial. Por defecto, se muestran los últimos 400 puntos. Se puede cambiar este número para ver con más detalle la trayectoria en el espacio de las fases

Angulo 1: Angulo 2:
Masa 2: Longitud 2:

Paso: Trayectoria: n. puntos:

Modos normales de vibración

Si nos restringimos a pequeños valores de los ángulos θ₁ y θ₂, las ecuaciones del movimiento se hacen mucho más simples. Desarrollamos en serie de Taylor cosθ y tomamos los dos primeros términos no nulos del desarrollo en serie

$\cos θ \approx 1 - \frac{1}{2} θ^{2}$

La energía potencial con esta aproximación, se expresa

$\begin{array}{l} E_{p} \approx - (m_{1} + m_{2}) g l_{1} (1 - \frac{1}{2} θ_{1}^{2}) - m_{2} g l_{2} (1 - \frac{1}{2} θ_{2}^{2}) = \\ \frac{1}{2} (m_{1} + m_{2}) g l_{1} θ_{1}^{2} + \frac{1}{2} m_{2} g l_{2} θ_{2}^{2} + cte \end{array}$

La energía cinética con esta aproximación, se expresa

$E_{k} \approx \frac{1}{2} (m_{1} + m_{2}) l_{1}^{2} {(\frac{d θ_{1}}{d t})}^{2} + \frac{1}{2} m_{2} l_{2}^{2} {(\frac{d θ_{2}}{d t})}^{2} + m_{2} l_{1} l_{2} (\frac{d θ_{1}}{d t}) (\frac{d θ_{2}}{d t})$

Las ecuaciones del movimiento de Lagrange nos llevan al sistema de dos ecuaciones diferenciales de segundo orden. La lagrangiana L=E_k-E_p con el símbolo $\dot{θ} = \frac{d θ}{d t}$

$\begin{array}{l} L = \frac{1}{2} (m_{1} + m_{2}) l_{1}^{2} {\dot{θ}}_{1}^{2} + \frac{1}{2} m_{2} l_{2}^{2} {\dot{θ}}_{2}^{2} + m_{2} l_{1} l_{2} {\dot{θ}}_{1} {\dot{θ}}_{2} - \frac{1}{2} (m_{1} + m_{2}) g l_{1} θ_{1}^{2} - \frac{1}{2} m_{2} g l_{2} θ_{2}^{2} \\ \frac{d}{d t} \frac{\partial L}{\partial {\dot{θ}}_{1}} - \frac{\partial L}{\partial θ_{1}} = 0 \\ \frac{d}{d t} \frac{\partial L}{\partial {\dot{θ}}_{2}} - \frac{\partial L}{\partial θ_{2}} = 0 \end{array}$

Las ecuaciones del movimiento son

$\begin{array}{l} (m_{1} + m_{2}) l_{1} \frac{d^{2} θ_{1}}{d t^{2}} + (m_{1} + m_{2}) g θ_{1} + m_{2} l_{2} \frac{d^{2} θ_{2}}{d t^{2}} = 0 \\ l_{2} \frac{d^{2} θ_{2}}{d t^{2}} + g θ_{2} + l_{1} \frac{d^{2} θ_{1}}{d t^{2}} = 0 \end{array}$

Calculamos las derivadas segundas respecto del tiempo de estas dos ecuaciones diferenciales

$\begin{array}{l} (m_{1} + m_{2}) l_{1} \frac{d^{4} θ_{1}}{d t^{4}} + (m_{1} + m_{2}) g \frac{d^{2} θ_{1}}{d t^{2}} + m_{2} l_{2} \frac{d^{4} θ_{2}}{d t^{4}} = 0 \\ l_{2} \frac{d^{4} θ_{2}}{d t^{4}} + g \frac{d^{2} θ_{2}}{d t^{2}} + l_{1} \frac{d^{4} θ_{1}}{d t^{4}} = 0 \end{array}$

Entre estas cuatro ecuaciones, eliminamos θ₂, obteniendo la ecuación diferencial de cuarto orden en θ₁.

$m_{1} l_{1} \frac{d^{4} θ_{1}}{d t^{4}} + (m_{1} + m_{2}) g (1 + \frac{l_{1}}{l_{2}}) \frac{d^{2} θ_{1}}{d t^{2}} + \frac{(m_{1} + m_{2}) g^{2}}{l_{2}} θ_{1} = 0$

Suponiendo una solución de la forma

θ₁=Asin(ωt)+Bcos(ωt) o bien, θ₁=Asin(ωt+φ)

Calculamos la derivada segunda y la derivada cuarta de θ₁ y las introducimos en la ecuación diferencial de cuarto orden, obteniendo la siguiente ecuación bicuadrada en ω.

$m_{1} l_{1} ω^{4} - (m_{1} + m_{2}) g (1 + \frac{l_{1}}{l_{2}}) ω^{2} + \frac{(m_{1} + m_{2}) g^{2}}{l_{2}} = 0$

Las dos raíces reales de esta ecuación son las frecuencias ω₁ y ω₂ de los modos normales de vibración

$\begin{array}{l} ω_{1}^{2} = \frac{(m_{1} + m_{2}) g}{2 m_{1} l_{1}} {(1 + \frac{l_{1}}{l_{2}}) - \sqrt{{(1 + \frac{l_{1}}{l_{2}})}^{2} - \frac{4 m_{1}}{(m_{1} + m_{2})}} \frac{l_{1}}{l_{2}}} \\ ω_{2}^{2} = \frac{(m_{1} + m_{2}) g}{2 m_{1} l_{1}} {(1 + \frac{l_{1}}{l_{2}}) + \sqrt{{(1 + \frac{l_{1}}{l_{2}})}^{2} - \frac{4 m_{1}}{(m_{1} + m_{2})}} \frac{l_{1}}{l_{2}}} \end{array}$

La forma general del ángulo θ₁ en función del tiempo t es una combinación de los dos modos normales de vibración

θ₁(t)=A₁sin(ω₁t)+ B₁cos(ω₁t)+ C₁sin(ω₂t)+ D₁cos(ω₂t)

Lo mismo para θ₂

θ₂(t)=A₂sin(ω₁t)+ B₂cos(ω₁t)+ C₂sin(ω₂t)+ D₂cos(ω₂t)

Las velocidades angulares son

$\begin{array}{l} \frac{d θ_{1}}{d t} = A_{1} ω_{1} \cos (ω_{1} t) - B_{1} ω_{1} \sin (ω_{1} t) + C_{1} ω_{2} \cos (ω_{2} t) - D_{1} ω_{2} \sin (ω_{2} t) \\ \frac{d θ_{2}}{d t} = A_{2} ω_{1} \cos (ω_{1} t) - B_{2} ω_{1} \sin (ω_{1} t) + C_{2} ω_{2} \cos (ω_{2} t) - D_{2} ω_{2} \sin (ω_{2} t) \end{array}$

Relacionamos los coeficientes A₁ y A₂, B₁ y B₂, C₁ y C₂, D₁ y D₂, calculando la derivada segunda de θ₂, la derivada segunda de θ₁ e introduciéndolos en una de las dos ecuaciones diferenciales del movimiento

$l_{2} \frac{d^{2} θ_{2}}{d t^{2}} + g θ_{2} + l_{1} \frac{d^{2} θ_{1}}{d t^{2}} = 0$

Tenemos cuatro relaciones

$\begin{array}{l} (- ω_{1}^{2} l_{2} + g) A_{2} - ω_{1}^{2} l_{1} A_{1} = 0 \\ (- ω_{1}^{2} l_{2} + g) B_{2} - ω_{1}^{2} l_{1} B_{1} = 0 \\ (- ω_{2}^{2} l_{2} + g) C_{2} - ω_{2}^{2} l_{1} C_{1} = 0 \\ (- ω_{2}^{2} l_{2} + g) D_{2} - ω_{2}^{2} l_{1} D_{1} = 0 \end{array}$

Las condiciones iniciales determinan los valores de los cuatro coeficientes A₁, B₁, C₁ y D₁ y por tanto, de los coeficientes A₂, B₂, C₂ y D₂, a través de las relaciones establecidas anteriormente.

Desplazamos el primer péndulo un ángulo θ₁₀ con respecto a la vertical y el segundo péndulo un ángulo θ₂₀ a continuación, los soltamos. La velocidad inicial es dθ₁/dt=0, dθ₂/dt=0 en el instante t=0.

Resolvemos el sistema de cuatro ecuaciones junto a las relaciones establecidas anteriormente.

θ₁₀=B₁+D₁0=ω₁·A₁+ ω₂·C₁θ₂₀=B₂+D₂0=ω₁·A₂+ ω₂·C₂

La solución de este sistema es

A₁=C₁=A₂=C₂=0

$\begin{array}{l} B_{2} = \frac{ω_{1}^{2} (ω_{2}^{2} l_{1} θ_{10} + ω_{2}^{2} l_{2} θ_{20} - g θ_{20})}{g (ω_{2}^{2} - ω_{1}^{2})} B_{1} = (\frac{- ω_{1}^{2} l_{2} + g}{ω_{1}^{2} l_{1}}) B_{2} \\ D_{2} = \frac{ω_{2}^{2} (- ω_{1}^{2} l_{1} θ_{10} - ω_{1}^{2} l_{2} θ_{20} + g θ_{20})}{g (ω_{2}^{2} - ω_{1}^{2})} D_{1} = (\frac{- ω_{2}^{2} l_{2} + g}{ω_{2}^{2} l_{1}}) D_{2} \end{array}$

La posición angular en función del tiempo t de cada una de las partículas es

θ₁(t)=B₁cos(ω₁t)+ D₁cos(ω₂t)
θ₂(t)=B₂cos(ω₁t)+D₂cos(ω₂t)

Modos normales de vibración

El modo 1 de frecuencia angular ω₁, se obtiene cuando D₂=0, la relación entre los ángulos iniciales de desviación de los dos péndulos es

$θ_{10} = \frac{g - ω_{1}^{2} l_{2}}{ω_{1}^{2} l_{1}} θ_{20}$

B₁=θ₁₀, B₂=θ₂₀

La posición angular en función del tiempo t de cada una de las partículas es

$\begin{array}{l} θ_{2} (t) = θ_{20} \cos (ω_{1} t) \\ θ_{1} (t) = θ_{10} \cos (ω_{1} t) \end{array}$

El modo 2 de frecuencia angular ω₂, se obtiene cuando B₂=0, la relación entre los ángulos iniciales de desviación de los dos péndulos es

$θ_{10} = \frac{g - ω_{2}^{2} l_{2}}{ω_{2}^{2} l_{1}} θ_{20}$

D₂=θ₂₀, y D₁=θ₁₀

La posición angular en función del tiempo t de cada una de las partículas es

$\begin{array}{l} θ_{2} (t) = θ_{20} \cos (ω_{2} t) \\ θ_{1} (t) = θ_{10} \cos (ω_{2} t) \end{array}$

Cuando los péndulos son iguales

Cuando m₁=m₂ y l₁=l₂ las frecuencias ω₁ y ω₂de los modos normales de vibración tienen una expresión mucho más simple

$ω_{1}^{2} = \frac{g}{l} (2 - \sqrt{2}) ω_{2}^{2} = \frac{g}{l} (2 + \sqrt{2})$

Los coeficientes B₂, B₁, D₂ y D₁ valen

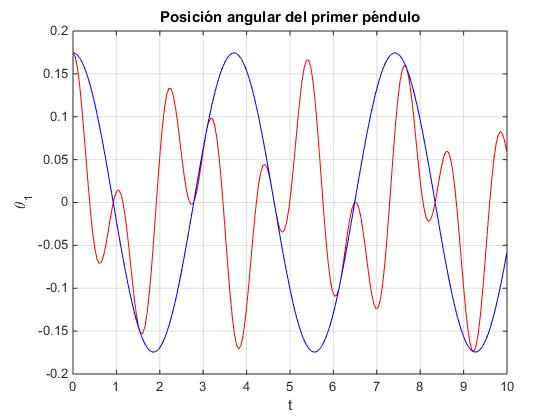
$\begin{array}{l} B_{2} = \frac{\sqrt{2} - 1}{2} ((2 + \sqrt{2}) (θ_{10} + θ_{20}) - θ_{20}) B_{1} = \frac{\sqrt{2}}{2} B_{2} \\ D_{2} = \frac{\sqrt{2} + 1}{2} (- (2 - \sqrt{2}) (θ_{10} + θ_{20}) + θ_{20}) D_{1} = - \frac{\sqrt{2}}{2} D_{2} \end{array}$

Es importante analizar el caso de que θ₂₀=0. Se desplaza el primer péndulo un ángulo θ₁₀ respecto de la vertical y se suelta

$\begin{array}{l} B_{2} = \frac{\sqrt{2}}{2} θ_{10} B_{1} = \frac{1}{2} θ_{10} \\ D_{2} = - \frac{\sqrt{2}}{2} θ_{10} D_{1} = \frac{1}{2} θ_{10} \end{array}$

Las ecuaciones del movimiento de cada unos de las partículas se escriben

$\begin{array}{l} θ_{1} (t) = \frac{1}{2} θ_{10} (\cos (ω_{1} t) + \cos (ω_{2} t)) = θ_{10} \cos (\frac{ω_{2} - ω_{1}}{2} t) \cos (\frac{ω_{2} + ω_{1}}{2} t) \\ θ_{2} (t) = \frac{\sqrt{2}}{2} θ_{10} (\cos (ω_{1} t) - \cos (ω_{2} t)) = \sqrt{2} θ_{10} \sin (\frac{ω_{2} - ω_{1}}{2} t) \sin (\frac{ω_{2} + ω_{1}}{2} t) \end{array}$

En la figura, se representa en color rojo θ₁(t) y en color azul la amplitud modulada $θ_{10} cos (\frac{ω_{2} - ω_{1}}{2} t)$

m1=1; %masa del primer péndulo
m2=1;  %masa del segundo péndulo
lon1=1;  %longitud del primer péndulo
lon2=1; %longitud del segundo péndulo
ang1=pi/18; %angulo inicial del primer péndulo
ang2=0; %angulo inicial del segundo péndulo

w1=((m1+m2)*9.8/(2*m1*lon1))*((1+lon1/lon2)
-sqrt((1+lon1/lon2)*(1+lon1/lon2)-4*m1*lon1/((m1+m2)*lon2)));
w2=((m1+m2)*9.8/(2*m1*lon1))*((1+lon1/lon2)
+sqrt((1+lon1/lon2)*(1+lon1/lon2)-4*m1*lon1/((m1+m2)*lon2)));
%coeficientes
B2=w1*(w2*lon1*ang1+w2*lon2*ang2-9.8*ang2)/(9.8*(w2-w1));
D2=w2*(-w1*lon1*ang1-w1*lon2*ang2+9.8*ang2)/(9.8*(w2-w1));
B1=(-w1*lon2+9.8)*B2/(w1*lon1);
D1=(-w2*lon2+9.8)*D2/(w2*lon1);

t=linspace(0,10,200);
y1=B1*cos(sqrt(w1)*t)+D1*cos(sqrt(w2)*t);
y2=B2*cos(sqrt(w1)*t)+D2*cos(sqrt(w2)*t);
  
figure
amplitud1=ang1*cos((sqrt(w2)-sqrt(w1))*t/2);
plot(t,y1,'r',t,amplitud1,'b')
grid on
xlabel('t')
ylabel('\theta_1')
title('Posición angular del primer péndulo')

figure
amplitud2=sqrt(2)*ang1*sin((sqrt(w2)-sqrt(w1))*t/2);
plot(t,y2,'r',t,amplitud2,'b')
grid on
xlabel('t')
ylabel('\theta_2')
title('Posición angular del segundo péndulo')

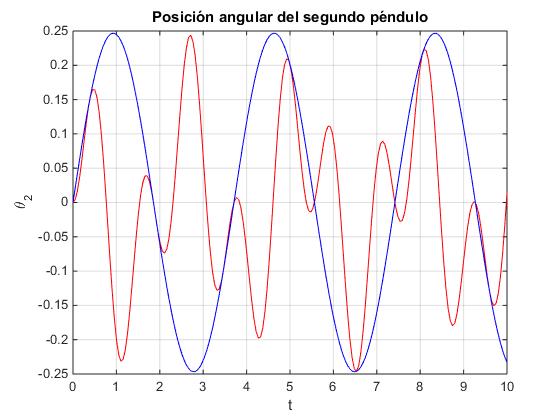
En la figura, se representa en color rojo θ₂(t) y en color azul la amplitud modulada $\sqrt{2} θ_{10} \sin (\frac{ω_{2} - ω_{1}}{2} t)$

El modo 1 de frecuencia angular ω₁, se obtiene cuando D₂=0, la relación entre los ángulos iniciales de desviación de los dos péndulos es

$θ_{10} = \frac{\sqrt{2}}{2} θ_{20}$

B₂=θ₂₀, y B₁=θ₁₀

La posición angular en función del tiempo t de cada una de las partículas es

$\begin{array}{l} θ_{2} (t) = θ_{20} \cos (ω_{1} t) \\ θ_{1} (t) = θ_{10} \cos (ω_{1} t) \end{array}$

El modo 2 de frecuencia angular ω₂, se obtiene cuando B₂=0, la relación entre los ángulos iniciales de desviación de los dos péndulos es

$θ_{10} = - \frac{\sqrt{2}}{2} θ_{20}$

D₂=θ₂₀, y D₁=θ₁₀

La posición angular en función del tiempo t de cada una de las partículas es

$\begin{array}{l} θ_{2} (t) = θ_{20} \cos (ω_{2} t) \\ θ_{1} (t) = θ_{10} \cos (ω_{2} t) \end{array}$

Actividades

Se introduce

La masa m₂ de la partícula del péndulo inferior en kg, en el control titulado Masa 2.
La masa de la partícula del péndulo superior se ha fijado en m₁=1 kg
La longitud l₂ del péndulo inferior en el control titulado Longitud 2.
La longitud del péndulo superior se ha fijado en l₁=1 m
El ángulo de desviación inicial θ₁₀ del péndulo superior en grados, en el control titulado Angulo 1.
El ángulo de desviación inicial θ₂₀ del péndulo inferior en grados, en el control titulado Angulo 2.

Se pulsa el botón titulado Nuevo

Se observa el movimiento de los dos péndulos y la representación gráfica del ángulo de desviación de cada péndulo θ₁ y θ₂ en función del tiempo t.

En la parte superior derecha, se muestra el valor de la energía total que permanece constante durante el movimiento de los péndulos.

Para observar los modos normales de vibración, se introducen los siguientes datos. Para el primer modo: Angulo 1, 7.07, Angulo 2, 10. Para el segundo modo: Angulo 1, -7.07, Angulo 2, 10

Angulo 1: Angulo 2:
Masa 2: Longitud 2:

Referencias

Lee S. M. The double-simple pendulum problem. Am. J. Phys. 38 (1970) pp. 536-537