Movimiento Armónico Simple

Una partícula describe un Movimiento Armónico Simple (M.A.S.) cuando se mueve a lo largo del eje X, estando su posición x dada en función del tiempo t por la ecuación

x=A·sin(ωt+φ)

• A es la amplitud.
• ω la frecuencia angular.
• φ la fase inicial.

• Periodo, $P=\frac{2\pi }{\omega }$

Condiciones iniciales

Posición x y velocidad v en cualquier instante t

${\displaystyle \begin{array}{l}x=A\sin (\omega t+\phi )\\ v=\frac{dx}{dt}=A\omega \cos (\omega t+\phi )\end{array}}$

Conociendo la posición inicial x₀ y la velocidad inicial v₀ en el instante t=0.

x₀=A·sinφ
v₀=Aω·cosφ

se determinan la amplitud A y la fase inicial φ

Energías

Energía potencial

${\displaystyle E_p(x)=\frac{1}{2}m{\omega }^2{x}^2}$

Energía cinética

${\displaystyle E_k=\frac{1}{2}m{v}^2}$

Osciladores

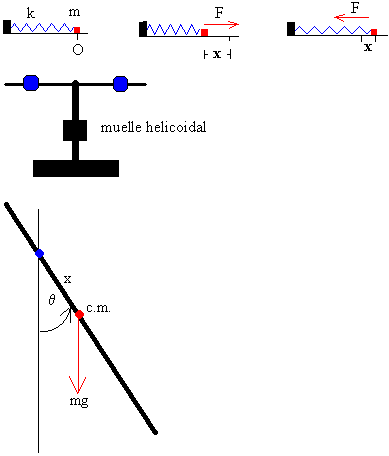
Muelle elástico

${\displaystyle P=2\pi \sqrt{\frac{m}{k}}}$

Péndulo de torsión

${\displaystyle P=2\pi \sqrt{\frac{I}{K}}}$

Péndulo compuesto

${\displaystyle P=2\pi \sqrt{\frac{I_o}{mgx}}}$

Composición de dos MAS de la misma dirección y frecuencia

• El primero con amplitud A₁, y fase inicial φ₁.

${\displaystyle x_1=A_1\sin (\omega t+{\phi }_1)}$

• el segundo con amplitud A₂, y fase inicial φ₂.

${\displaystyle x_2=A_2\sin (\omega t+{\phi }_2)}$

El resultado es un M.A.S. de la misma dirección y de la misma frecuencia

${\displaystyle x=A\sin (\omega t+\phi )}$

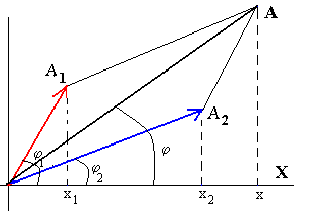
La amplitud y fase inicial se pueden obtener a partir de la figura, sumando los vectores rotatorios que representan a cada uno de los dos M.A.S. componentes.

${\displaystyle \overrightarrow{A}=\overrightarrow{A_1}+\overrightarrow{A_2}}$