Expresamos la solución particular de la ecuación diferencial que describe el oscilador forzado, de la forma

x₂=Acos(ω_f t)+Bsin(ω_f t)

o de la forma equivalente

${\displaystyle \begin{array}{l}x=A_0\sin \left({\omega }_{f}t-\delta \right)\\ x=A_0\cos \delta \sin \left({\omega }_{f}t\right)-A_0\sin \delta \cos \left({\omega }_{f}t\right)\end{array}}$

Obtendremos los valores de A₀ y δ a través de los parámetros A y B de la solución particular de la ecuación diferencial que ya hemos calculado.

${\displaystyle \begin{array}{l}{A}_0\sin \delta =-\frac{F_0\left({\omega }_0^2-{\omega }_f^2\right)}{m\left({\left({\omega }_0^2-{\omega }_f^2\right)}^2+4{\gamma }^2{\omega }_f^2\right)}\\ A_0\cos \delta =\frac{2\gamma {\omega }_f{F}_0}{m\left({\left({\omega }_0^2-{\omega }_f^2\right)}^2+4{\gamma }^2{\omega }_f^2\right)}\\ A_0=\frac{F_0/m}{\sqrt{{\left({\omega }_0^2-{\omega }_f^2\right)}^2+4{\gamma }^2{\omega }_f^2}}\tan \delta =\frac{{\omega }_f^2-{\omega }_0^2}{2\gamma {\omega }_f}\end{array}}$

El cosδ es siempre positivo y el sinδ es positivo cuando ω_f>ω₀ y negativo cuando ω_f<ω₀. Es decir, el desfase δ varía entre -π/2 y +π/2.

Comparamos el estado transitorio y su evolución hacia el estado estacionario, de un oscilador que parte del origen x₀=0, en reposo, v₀=0

Establecemos los siguientes valores:

• Coeficiente de rozamiento γ=7;
• Frecuencia angular propia, ω₀=100 rad/s y
• Frecuencia de la fuerza oscilante, ω_f=120 rad/s

wf=120; %frecuencia de la fuerza oscilante
w0=100; %frecuencia natural
gamma=7; %amortiguamiento
w=sqrt(w0^2-gamma^2);
x=@(t) ((w0^2-wf^2)*(cos(wf*t)-exp(-gamma*t).*cos(w*t))+
2*gamma*wf*(sin(wf*t)-(w0^2+wf^2)*exp(-gamma*t).*sin(w*t)/(2*w*wf)))
/((w0^2-wf^2)^2+4*gamma^2*wf^2);
%estado estacionario
A=1/sqrt((w0^2-wf^2)^2+4*gamma^2*wf^2); 
delta=atan((wf^2-w0^2)/(2*gamma*wf));
hold on
fplot(x,[0,0.2*pi])
fplot(@(t) A*sin(wf*t-delta),[0,0.2*pi])
hold off
grid on
legend('transitorio','estacionario','Location','southeast')
xlabel('t')
ylabel('\theta')
title('Oscilaciones forzadas')

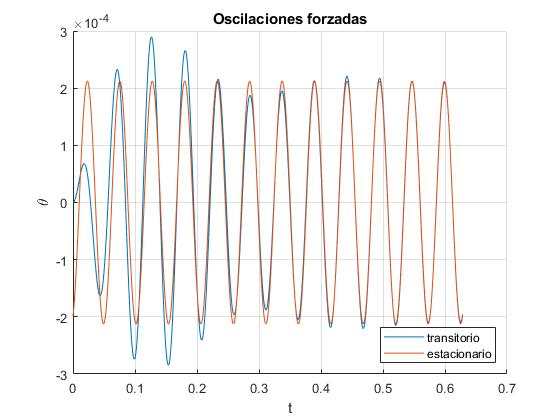
Al cabo de un cierto tiempo t≈0.5 s, el estado estacionario coincide con el transitorio

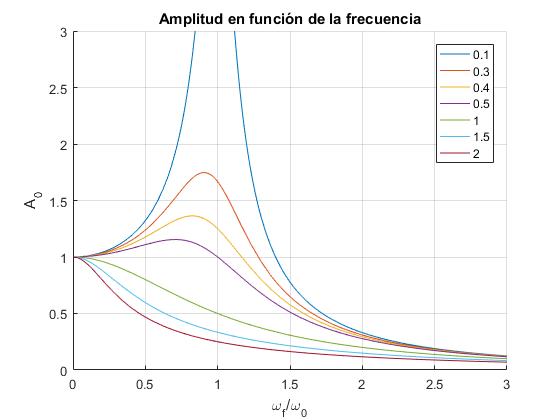
En la figura (más abajo), se muestra la respuesta en amplitud de la oscilación forzada, en el estado estacionario.

Derivando la expresión de la amplitud A₀ en función de la frecuencia de la fuerza oscilante, respecto de ω_f, e igualando a cero, obtenemos la frecuencia ω_f para la cual la amplitud en el estado estacionario presenta un máximo

${\displaystyle \frac{d{A}_0}{d{\omega }_f}=-\frac{F_0}{m}\frac{2\left({\omega }_f^2-{\omega }_0^2\right)(-2{\omega }_f)+8{\gamma }^2{\omega }_f}{2{\left({\left({\omega }_f^2-{\omega }_0^2\right)}^2+4{\omega }_f^2{\gamma }^2\right)}^{3/2}}=0{\omega }_f=\sqrt{{\omega }_0^2-2{\gamma }^2}}$

• En el caso ideal de que no existiese rozamiento γ=0, la amplitud de la oscilación forzada se haría muy grande, tendería a infinito, cuando la frecuencia ω_f de la fuerza oscilante es igual a la frecuencia propia del oscilador ω₀.
• En el caso habitual de que exista rozamiento (γ>0), la amplitud se hace máxima cuando la frecuencia ω_f de la fuerza oscilante es próxima a la natural del oscilador ω₀

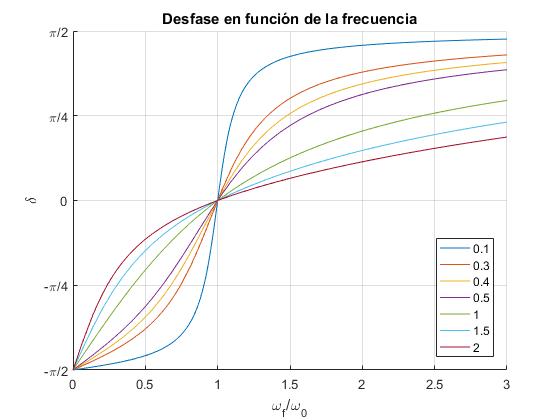
La característica esencial del estado estacionario, es que la velocidad de la partícula

${\displaystyle v=\frac{dx}{dt}=A_0{\omega }_f\cos ({\omega }_{f}t-\delta )}$

está en fase δ=0 con la fuerza oscilante cuando la frecuencia de la fuerza oscilante ω_f es igual a la frecuencia propia del oscilador ω₀.

Expresamos la amplitud A₀ y la fase δ en términos de los cocientes r=ω_f/ω₀ y ξ=γ/ω₀.

${\displaystyle A_0=\frac{F_0/m}{{\omega }_0^2}\frac{1}{\sqrt{{\left(r^2-1\right)}^2+4r^2{\xi }^2}}\tan \delta =\frac{r^2-1}{2r\xi }}$

Representamos la amplitud en función de r=ω/ω₀ para varios valores de la constante de amortiguamiento ξ

hold on
for x=[0.1 0.3 0.4 0.5 1 1.5 2]
    f=@(r) 1./sqrt((r.^2-1).^2+4*r.^2*x^2);
    fplot(f,[0,3],'displayName',num2str(x))
end
hold off
ylim([0 3])
grid on
title('Amplitud en función de la frecuencia')
xlabel('\omega_f/\omega_0')
ylabel('A_0')
legend('-DynamicLegend','location','Northeast')

Representamos la fase δ en función de r=ω/ω₀ para varios valores de la constante de amortiguamiento ξ

hold on
for x=[0.1 0.3 0.4 0.5 1 1.5 2] %amortiguamiento
    f=@(r) atan((r.^2-1)./(2*r*x));
    fplot(f,[0,3],'displayName',num2str(x))
end
hold off
set(gca,'YTick',-pi/2:pi/4:pi/2)
set(gca,'YTickLabel',{'-\pi/2','-\pi/4','0','\pi/4','\pi/2'})
grid on
ylim([-pi/2,pi/2])
title('Desfase en función de la frecuencia')
xlabel('\omega_f/\omega_0')
ylabel('\delta')
legend('-DynamicLegend','location','Southeast')

Práctica de laboratorio

Con el dispositivo de PASCO, medimos el periodo P₀=1.45 s y frecuencia f₀=1/1.45 Hz, de las oscilaciones libres

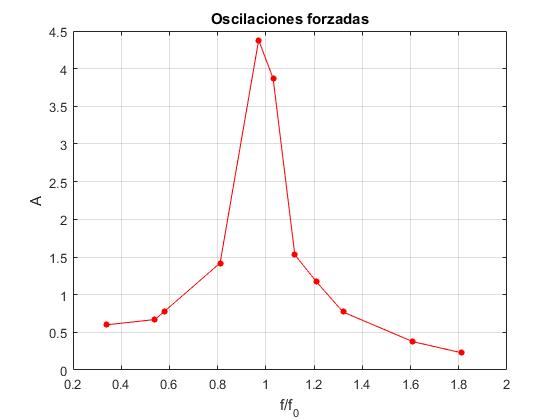
Conectamos la fuerza oscilante, un motor de velocidad angular variable a un generador de corriente contínua, esperamos un tiempo hasta que decaiga el estado transitorio. Las medidas de la amplitud A y del periodo P_f de las oscilaciones en el estado estacionario, tomadas por una estudiante de primer curso del Grado en Ingeniería de Energías Renovables han sido las siguientes:

x=[0.34,0.54,0.58,0.81,0.97,1.03,1.12,1.21,1.32,1.61,1.81];
y=[0.60,0.67,0.78,1.42,4.38,3.87,1.53,1.17,0.77,0.376,0.23];
plot(x,y,'-ro','markersize',4,'markeredgecolor','r','markerfacecolor','r')
grid on
xlabel('f/f_0')
ylabel('A')
title('Oscilaciones forzadas')

Energía del oscilador forzado. Resonancia

La energía de la partícula de masa m unida a un muelle elástico de constante k es la suma de la energía cinética y potencial

${\displaystyle \begin{array}{l}x=A_0\sin \left({\omega }_{f}t-\delta \right)\\ v=\frac{dx}{dt}=A_0{\omega }_f\cos \left({\omega }_{f}t-\delta \right)\\ E_k=\frac{1}{2}m{v}^2=\frac{1}{2}m{A}_0^2{\omega }_f^2{\cos }^2\left({\omega }_{f}t-\delta \right)\\ E_p=\frac{1}{2}k{x}^2=\frac{1}{2}m{A}_0^2{\omega }_0^2{\sin }^2\left({\omega }_{f}t-\delta \right)\\ E=E_k+E_p=\frac{1}{2}m{\omega }_0^2{A}_0^2\left({\omega }_f^2{\cos }^2\left({\omega }_{f}t-\delta \right)+{\omega }_0^2{\sin }^2\left({\omega }_{f}t-\delta \right)\right)\end{array}}$

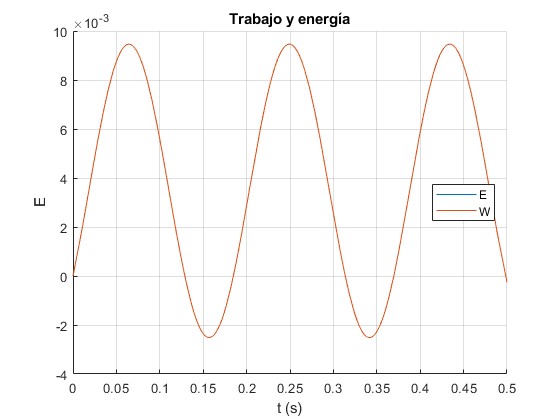
El trabajo W₁ de la fuerza oscilante es

${\displaystyle \begin{array}{l}{W}_1={\displaystyle \underset{0}{\overset{t}{\int }}{F}_0\cos \left({\omega }_{f}t\right)dx}={\displaystyle \underset{0}{\overset{t}{\int }}{F}_0\cos \left({\omega }_{f}t\right)vdt}={\displaystyle \underset{0}{\overset{t}{\int }}{F}_0\cos \left({\omega }_{f}t\right)A_0{\omega }_f\cos \left({\omega }_{f}t-\delta \right)dt}=\\ F_0{A}_0{\omega }_f{\displaystyle \underset{0}{\overset{t}{\int }}\left({\cos }^2\left({\omega }_{f}t\right)\cos \delta +\frac{1}{2}\sin \left(2{\omega }_{f}t\right)\sin \delta \right)dt}=\\ F_0{A}_0{\omega }_f\left\{\cos \delta {\displaystyle \underset{0}{\overset{t}{\int }}\frac{1+\cos \left(2{\omega }_{f}t\right)}{2}dt+\frac{1}{2}\sin \delta {\displaystyle \underset{0}{\overset{t}{\int }}\sin \left(2{\omega }_{f}t\right)dt}}\right\}\\ W_1=F_0{A}_0\left\{\frac{\cos \delta }{2}\left({\omega }_{f}t+\frac{1}{2}\sin \left(2{\omega }_{f}t\right)\right)+\frac{\sin \delta }{4}\left(1-\cos \left(2{\omega }_{f}t\right)\right)\right\}\end{array}}$

El trabajo W₂ de la fuerza de rozamiento es

${\displaystyle \begin{array}{l}{W}_2={\displaystyle \underset{0}{\overset{t}{\int }}-\lambda v·dx}=-2\gamma m{\displaystyle \underset{0}{\overset{t}{\int }}{v}^{2}dt}=-2\gamma m{\displaystyle \underset{0}{\overset{t}{\int }}{A}_0^2{\omega }_f^2{\cos }^2\left({\omega }_{f}t-\delta \right)dt}=\\ -2\gamma m{A}_0^2{\omega }_f^2{\displaystyle \underset{0}{\overset{t}{\int }}{\cos }^2\left({\omega }_{f}t-\delta \right)dt}=-2\gamma m{A}_0^2{\omega }_f^2{\displaystyle \underset{0}{\overset{t}{\int }}\frac{1+\cos \left(2{\omega }_{f}t-2\delta \right)}{2}dt}\\ W_2=-\gamma m{A}_0^2{\omega }_f\left\{{\omega }_{f}t+\frac{\sin \left(2{\omega }_{f}t-2\delta \right)}{2}+\frac{\sin \left(2\delta \right)}{2}\right\}\end{array}}$

Comprobamos que el trabajo de ambas fuerzas es igual a la variación de la energía del sistema formado por la partícula unida al muelle elástico

${\displaystyle W=W_1+W_2=E(t)-E(0)}$

m=1; %masa
F0=1; %fuerza
g=1/2; %gamma
w0=16; %frecuencia angular natural
wf=17; %frecuencia de la fuerza oscilante
A=(F0/m)/sqrt((w0^2-wf^2)^2+4*g^2*wf^2); %amplitud
delta=atan((wf^2-w0^2)/(2*g*wf)); %fase
%energía
E=@(t) m*A^2*(w0^2*sin(wf*t-delta).^2+wf^2*cos(wf*t-delta).^2)/2; 
%trabajo de la fuerza oscilante
W1=@(t) F0*A*(cos(delta)*(wf*t+sin(2*wf*t)/2)+sin(delta)*(1-cos(2*wf*t))/2)/2;
%trabajo de la fuerza de rozamiento
W2=@(t) -(wf*t+sin(2*wf*t-2*delta)/2+sin(2*delta)/2)*g*m*A^2*wf;

hold on
e=@(t) E(t)-E(0);
w=@(t) W1(t)+W2(t);
fplot(e, [0,0.5])
fplot(w, [0,0.5])
hold off
grid on
xlabel('t (s)')
ylabel('E,W')
title('Trabajo y energía')

La función W₁(t)+W₂(t) coincide con la función E(t)-E(0)

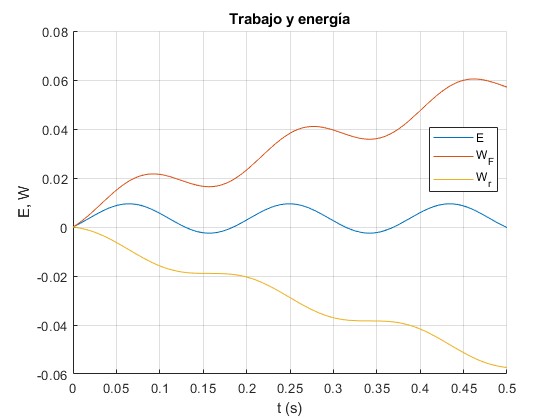
Representamos por separado el trabajo de la fuerza oscilante W₁(t), el trabajo de la fuerza de rozamiento W₂(t) y la variación de energía, E(t)-E(0)

F0=1; %fuerza
g=1/2; %gamma
w0=16; %frecuencia angular natural
wf=17; %frecuencia de la fuerza oscilante
A=(F0/m)/sqrt((w0^2-wf^2)^2+4*g^2*wf^2); %amplitud
delta=atan((wf^2-w0^2)/(2*g*wf)); %fase
%energía
E=@(t) m*A^2*(w0^2*sin(wf*t-delta).^2+wf^2*cos(wf*t-delta).^2)/2;  
%trabajo de la fuerza oscilante
W1=@(t) F0*A*(cos(delta)*(wf*t+sin(2*wf*t)/2)+sin(delta)*(1-cos(2*wf*t))/2)/2; 
%trabajo de la fuerza de rozamiento
W2=@(t) -(wf*t+sin(2*wf*t-2*delta)/2+sin(2*delta)/2)*g*m*A^2*wf;

hold on
e=@(t) E(t)-E(0);
fplot(e, [0,0.5])
fplot(W1, [0,0.5])
fplot(W2, [0,0.5])
hold off
grid on
xlabel('t (s)')
legend('E','W_F','W_r','location','best')
ylabel('E,W')
title('Trabajo y energía')

Resonancia

Denotemos por valor medio de una función periódica f(t) de periodo P a

${\displaystyle \langle f(t)\rangle =\frac{1}{P}{\displaystyle {\int }_0^{P}f(t)dt}}$

Calculemos el valor medio de la energía por unidad de tiempo suministrada por la fuerza oscilante

${\displaystyle P_1=\langle F_0\cos ({\omega }_{f}t)\cdot v\rangle }$

El valor medio de la energía por unidad de tiempo que disipa el oscilador a causa de su interacción con el medio que le rodea. Dicha interacción se describe en términos de una fuerza de rozamiento proporcional a la velocidad λv.

${\displaystyle P_2=\langle \lambda v\cdot v\rangle }$

En el estado estacionario

x=A₀·sin(ω_f·t-δ)
v=ω_f·A₀·cos(ω_f·t-δ)

Haciendo algunas operaciones, se obtiene la misma expresión para P₁ y para P₂.

${\displaystyle P_1=P_2=\frac{F_0^2\gamma {\omega }_f^2/m}{{\left({\omega }_f^2-{\omega }_0^2\right)}^2+4{\gamma }^2{\omega }_f^2}}$

Nota: para el cálculo con MATLAB utilizamos la expresión de x=A·cos(ω_f·t)+B·sin(ω_f·t) de la solución de la ecuación diferencial en vez de x=A₀·sin(ω_f·t-δ) del párrafo anterior.

>> syms F wf w0 g t;
>> A=F*(w0^2-wf^2)/((w0^2-wf^2)^2+4*wf^2*g^2);
>> B=2*g*wf*F/((w0^2-wf^2)^2+4*wf^2*g^2);
>> x=A*cos(wf*t)+B*sin(wf*t);
>> v=diff(x,t);
>> p=F*cos(wf*t)*v;
>> pot_1=int(p,t,0,P)/P %integramos respecto de t entre los límites 0 y P
pot_1 =(F^2*g*wf^2)/((w0^2 - wf^2)^2 + 4*g^2*wf^2)
>> f=2*g*v^2;
>> P=2*pi/wf; %periodo
>> pot_2=int(f,t,0,P)/P
pot_2 =(F^2*g*wf^2)/(w0^4 + wf^4 + wf^2*(4*g^2 - 2*w0^2))

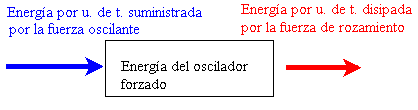
En el estado estacionario, el valor medio de la energía por unidad de tiempo suministrada por la fuerza oscilante, es igual al valor medio de la energía por unidad de tiempo que disipa el oscilador a causa de su interacción con el medio que le rodea. Manteniéndose la energía del oscilador forzado constante en valor medio.

Escribimos la expresión anterior de una forma más simple

${\displaystyle P=\frac{F_0^2}{4m{\gamma }^2}\left(\frac{1}{1+X^2}\right)X=\tan \delta =\frac{{\omega }_f^2-{\omega }_0^2}{2\gamma {\omega }_f}}$

Cuando la frecuencia ω_f de la fuerza oscilante es igual a la frecuencia ω₀ natural del oscilador la fuerza oscilante F₀·cos(ω_f t) y la velocidad v del oscilador están en fase δ=0, el valor medio de la energía por unidad de tiempo P suministrada por la fuerza oscilante es máxima. Esta situación recibe el nombre de resonancia.

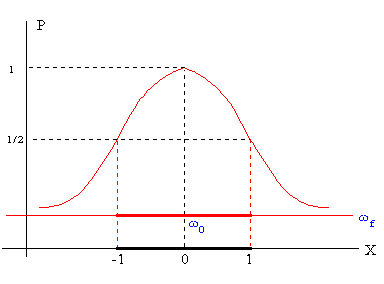
La representación de la potencia P en función de X tiene la forma de la curva acampanada de la figura. El máximo de la potencia P se obtiene para X=0, o bien, cuando la frecuencia ω_f de la fuerza oscilante es igual a la frecuencia ω₀ natural del oscilador.

Vemos también que la función es simétrica, tiene el mismo valor para X positivos y X negativos, y que P tiende rápidamente a cero a medida que X se hace mayor o menor que cero, es decir, a medida que la frecuencia ω_f de la fuerza oscilante se hace mayor o menor que la frecuencia ω₀ propia del oscilador.

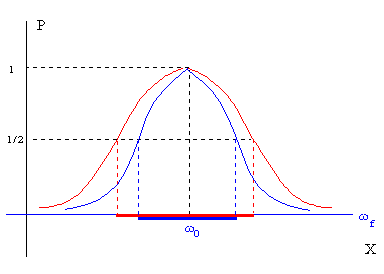
La anchura es otra característica importante de la curva. Se define como el intervalo de frecuencias de la fuerza oscilante para los cuales la potencia P es mayor que la mitad de la máxima. El intervalo de frecuencias ω_f alrededor de la frecuencia ω₀ propia del oscilador está comprendido entre X=-1 a X=+1, y vale aproximadamente 2γ.

En la figura, se representan dos curvas con la misma frecuencia de resonancia pero con disinta anchura.

El acelerómetro

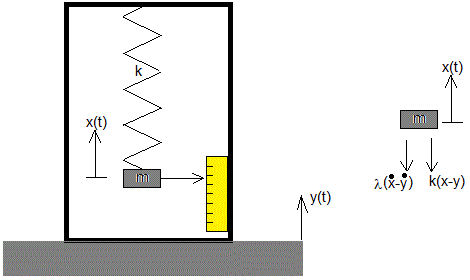
Un acelerómetro consta de un sistema masa-muelle elástico con rozamiento proporcional a la velocidad, situado sobre un soporte que vibra con frecuencia angular ω, de la forma y(t)=y₀sin(ωt) y por tanto, con aceleración

${\displaystyle \frac{d^{2}y}{d{t}^2}=-{\omega }^2{y}_0\sin \left(\omega t\right)}$

La aguja indicadora unida a la masa m, señala en la escala el desplazamiento relativo z(t)=x(t)-y(t).

${\displaystyle \frac{d^{2}x}{d{t}^2}=\frac{d^{2}z}{d{t}^2}-{\omega }^2{y}_0\sin \left(\omega t\right)}$

En la parte derecha de la figura, hemos dibujado las fuerzas sobre la partícula de masa m. La ecuación del movimiento es

${\displaystyle m\frac{d^{2}x}{d{t}^2}=-k(x-y)-\lambda \left(\frac{dx}{dt}-\frac{dy}{dt}\right)}$

El muelle de constante k se deforma x-y. La velocidad relativa de la partícula es dx/dt-dy/dt por tanto, la fuerza de rozamiento es proporcional a esta velocidad

${\displaystyle \frac{d^{2}z}{d{t}^2}+2\gamma \frac{dz}{dt}+{\omega }_0^{2}z={\omega }^2{y}_0\sin \left(\omega t\right)}$

que es similar a la ecuación diferencial de las oscilaciones forzadas. La solución particular es z=Asin(ωt)+Bcos(ωt), que es la que corresponde al estado estacionario.

Introducimos z e la ecuación diferencial y obtenemos el sistema de dos ecuaciones

${\displaystyle \begin{array}{l}\{\begin{array}{l}\left({\omega }_0^2-{\omega }^2\right)A-2\gamma \omega B={\omega }^2{y}_0\\ \left({\omega }_0^2-{\omega }^2\right)B+2\gamma \omega A=0\end{array}\\ A=\frac{\left({\omega }_0^2-{\omega }^2\right)\left({\omega }^2{y}_0\right)}{{\left({\omega }_0^2-{\omega }^2\right)}^2+4{\gamma }^2{\omega }^2}B=-\frac{2\gamma \omega \left({\omega }_0^2-{\omega }^2\right)}{{\left({\omega }_0^2-{\omega }^2\right)}^2+4{\gamma }^2{\omega }^2}\end{array}}$

Calculamos la amplitud z₀ y la fase δ de la expresión equivalente, z=z₀sin(ωt-δ)

${\displaystyle \begin{array}{l}{z}_0\cos \delta =A\\ z_0\sin \delta =-B\end{array}\}{z}_0=\frac{{\omega }^2{y}_0}{\sqrt{{\left({\omega }_0^2-{\omega }^2\right)}^2+4{\gamma }^2{\omega }^2}}\tan \delta =\frac{2\gamma \omega }{{\omega }_0^2-{\omega }^2}}$

Llamando r=ω/ω₀ y ξ=γ/ω₀

${\displaystyle z_0=\frac{r^2{y}_0}{\sqrt{{\left(1-r^2\right)}^2+4{\xi }^2{r}^2}}\tan \delta =\frac{2\xi r}{1-r^2}}$

Representamos la amplitud z₀/y₀ en función de r para varios valores de la constante de amortiguamiento ξ

hold on
for x=[0,0.3,0.5,0.7,1]
    z=@(r) (r.^2)./sqrt((1-r.^2).^2+4*x^2*r.^2);
    fplot(z,[0,5],'displayName',num2str(x))
end
hold off
grid on
ylim([0,3])
legend('-DynamicLegend','location','northeast')
xlabel('r')
ylabel('z_0/y_0')
title('Amplitud')

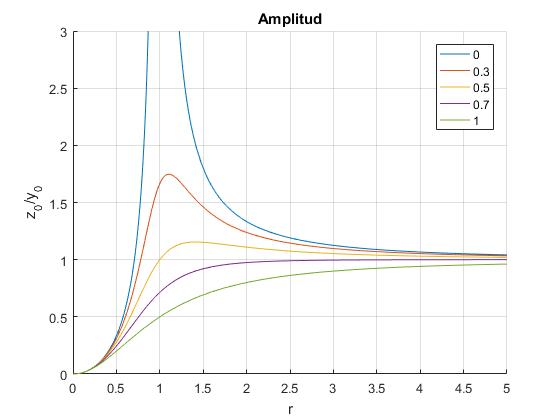
Como podemos apreciar, la amplitud z₀/y₀≈1 para r grande. Midiendo z₀ sabemos y₀ con un cierto margen de error

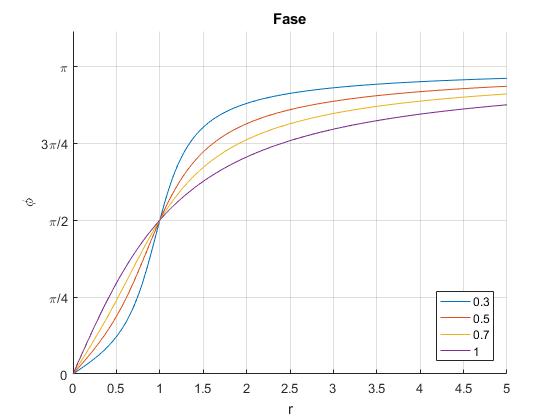
Representamos la fase δ para varios valores de la constante de amortiguamiento ξ

hold on
r=linspace(0,5,100);
for x=[0.3,0.5,0.7,1]
    phi=atan(2*x*r./(1-r.^2));
    phi=(phi<0)*pi+phi;
    plot(r,phi,'displayName',num2str(x))
end
hold off
grid on
legend('-DynamicLegend','location','southeast')
set(gca,'YTick',0:pi/4:pi)
set(gca,'YTickLabel',{'0','\pi/4','\pi/2','3\pi/4','\pi'})
xlabel('r')
ylabel('\delta')
title('Fase')