Movimiento Armónico Simple

Una partícula describe un Movimiento Armónico Simple (M.A.S.) cuando se mueve a lo largo del eje X, estando su posición x dada en función del tiempo t por la ecuación

x=A·sin(ωt+φ)

donde

A es la amplitud.
ω la frecuencia angular.
ω t+φ la fase.
φ la fase inicial.

Las características de un M.A.S. son:

Como los valores máximo y mínimo de la función seno son +1 y -1, el movimiento se realiza en una región del eje X comprendida entre -A y +A.
La función seno es periódica y se repite cada 2π, por tanto, el movimiento se repite cuando el argumento de la función seno se incrementa en 2π, es decir, cuando transcurre un tiempo P tal que ω(t+P)+φ=ω t+φ+2π .

$P = \frac{2 π}{ω}$

Se denomina frecuencia f a la inversa del periodo P. La frecuencia se mide en Hz (Hercio) en honor a Hertz. La ecuación de un MAS se escribe

x=A·sin(2πf·t+φ)

Examinamos utilizando MATLAB el papel de la amplitud A, frecuencia f y fase inicial φ

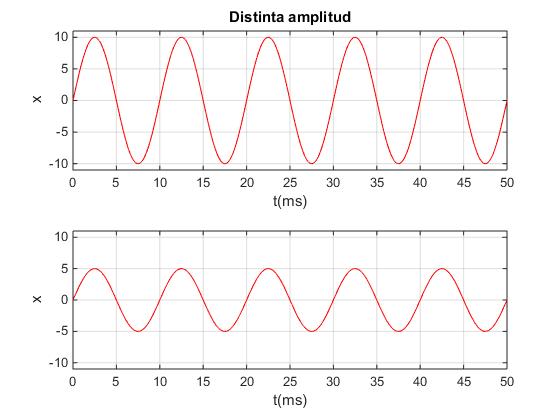
Dos amplitudes distintas, A=10 y A=5 y la misma frecuencia f=100 Hz, (el tiempo se mide en milisegundos, ms)

subplot(2,1,1)
t=0:0.1:50; %en milisegundos
x=10*sin(2*pi*0.1*t); %amplitud 10
plot(t,x,'r')
xlabel('t(ms)')
ylabel('x')
title('Distinta amplitud')
ylim([-11,11])
grid on

subplot(2,1,2)
x=5*sin(2*pi*0.1*t); %amplitud 5
plot(t,x,'r')
ylim([-10,10])
xlabel('t(ms)')
ylabel('x')
ylim([-11,11])
grid on

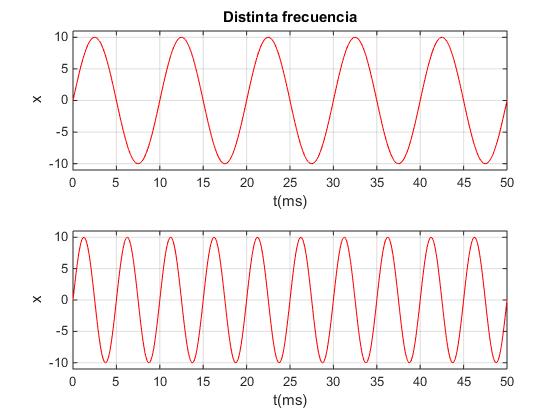
La misma amplitud A=10, dos frecuencias distintas f=100 y f=200 Hz

subplot(2,1,1)
t=0:0.1:50; %milisegundos
x=10*sin(2*pi*0.1*t); %frecuencia, 100 Hz
plot(t,x,'r')
xlabel('t(ms)')
ylabel('x')
title('Distinta frecuencia')
ylim([-11,11])
grid on

subplot(2,1,2)
x=10*sin(2*pi*0.2*t);  %frecuencia, 200 Hz
plot(t,x,'r')
xlabel('t(ms)')
ylabel('x')
ylim([-11,11])
grid on

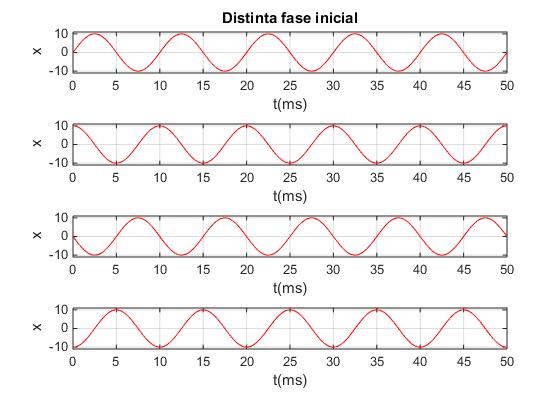
Fases iniciales distintas: 0, π/2, π,3π/2, misma frecuencia f=100 Hz y misma amplitud A=10

subplot(4,1,1)
t=0:0.1:50; %milisegundos
x=10*sin(2*pi*0.1*t);
plot(t,x,'r')
xlabel('t(ms)')
ylabel('x')
title('Distinta fase inicial')
ylim([-11,11])
grid on

subplot(4,1,2)
x=10*sin(2*pi*0.1*t+pi/2);
plot(t,x,'r')
xlabel('t(ms)')
ylabel('x')
ylim([-11,11])
grid on

subplot(4,1,3)
x=10*sin(2*pi*0.1*t+pi);
plot(t,x,'r')
xlabel('t(ms)')
ylabel('x')
ylim([-11,11])
grid on

subplot(4,1,4)
x=10*sin(2*pi*0.1*t+3*pi/2);
plot(t,x,'r')
xlabel('t(ms)')
ylabel('x')
ylim([-11,11])
grid on

Cinemática de un M.A.S.

La posición del móvil que describe un M.A.S. en función del tiempo viene dada por la ecuación

x=A·sin(ωt+φ)

Derivando con respecto al tiempo, obtenemos la velocidad del móvil

$v = \frac{d x}{d t} = A ω \cdot \cos (ω t + φ)$

Derivando de nuevo respecto del tiempo, obtenemos la aceleración del móvil

$a = \frac{d v}{d t} = - A ω^{2} \cdot \sin (ω t + φ) = - ω^{2} x$

M.A.S y movimiento circular

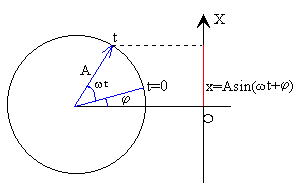
La ecuación de un M.A.S. es

x=A·sin(ωt+φ)

En la figura, se observa la interpretación de un M.A.S. como proyección sobre el eje X, del extremo de un vector rotatorio de longitud igual a la amplitud A, que gira con velocidad angular ω igual a la frecuencia angular del M.A.S, en el sentido contrario a las agujas del reloj.

El ángulo ω t+φ que forma el vector rotatorio con el eje de las X se denomina fase del movimiento. El ángulo φ que forma en el instante t=0, se denomina fase inicial.

Se introduce

la amplitud A, en el control titulado Amplitud
la frecuencia angular ω, en el control titulado Frecuencia
la fase inicial φ (en grados), en el control de edición titulado Fase inicial

Se pulsa en el botón titulado Nuevo.

Amplitud: Frecuencia:
Fase inicial :

Dinámica de un M.A.S.

Aplicando la segunda ley de Newton obtenemos la expresión de la fuerza necesaria para que un móvil de masa m describa un M.A.S. Esta fuerza es proporcional al desplazamiento x y de sentido contrario a éste.

$F = m a = - m ω^{2} x$

Como la fuerza F es conservativa. El trabajo de dicha fuerza es igual a la diferencia entre el valor inicial y el final de la energía potencial E_p.

$\begin{array}{l} \int_{x_{1}}^{x_{2}} F \cdot d x = E_{p 1} - E_{p 2} \\ \int_{x_{1}}^{x_{2}} F \cdot d x = \int_{x_{1}}^{x_{2}} - m ω^{2} x \cdot d x = - {\frac{1}{2} m ω^{2} x^{2} |}_{x_{1}}^{x_{2}} = \frac{1}{2} m ω^{2} x_{1}^{2} - \frac{1}{2} m ω^{2} x_{2}^{2} \end{array}$

La expresión de la energía potencial es

$E_{p} (x) = \frac{1}{2} m ω^{2} x^{2} + c$

Donde c es cualquier constante. Se toma como nivel cero de la energía potencial E_p=0 cuando el móvil está en el origen, x=0, por lo que c=0

La energía total E, es la suma de la energía cinética E_k y de la energía potencial E_p que es constante.

$\begin{array}{l} E = E_{k} + E_{p} = \frac{1}{2} m v^{2} + \frac{1}{2} m ω^{2} x^{2} = \\ \frac{1}{2} m ω^{2} A^{2} \cos^{2} (ω t + φ) + \frac{1}{2} m ω^{2} A^{2} \sin^{2} (ω t + φ) = \frac{1}{2} m ω^{2} A^{2} \end{array}$

Curva de energía potencial

La función $E_{p} = \frac{1}{2} m ω^{2} x^{2}$ representa una parábola cuyo vértice está en el origen, que tiene un mínimo en x=0 cuyo valor es E_p=0.

Las región donde se puede mover la partícula está determinada por la condición de que la energía cinética ha de ser mayor o igual a cero E_k>=0. En otras palabras, que la energía total sea mayor o igual que la energía potencial E>=E_p. Si la partícula tiene una energía total E, la partícula solamente se podrá mover en la región comprendida entre -A y +A, siendo A la amplitud de su M.A.S.

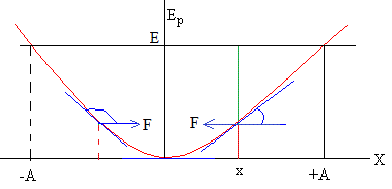
El módulo y el sentido de la fuerza vienen dados por la pendiente de la recta tangente cambiada de signo. Por tanto, la fuerza que actúa sobre la partícula es negativa a la derecha del origen y positiva a la izquierda.

$F = - \frac{d E_{p}}{d x} = - m ω^{2} x$

En el origen la pendiente es nula, la fuerza es nula, una situación de equilibrio, que por coincidir con un mínimo de la energía potencial es de carácter estable.

La energía total E de la partícula está representada por el segmento vertical de color negro. En un punto x el segmento vertical de color rojo representa la energía potencial E_p y el segmento de color verde la energía cinética E_k

En un sistema conservativo dibujamos la curva de la energía potencial E_p(x) y una línea horizontal a una altura E, que representa la energía total. De este modo, podemos describir cualitativamente el movimiento de la partícula: los intervalos x en los que se puede mover, las posiciones donde su velocidad es máxima o mínima, las posiciones de equilibrio (F=0), etc.

Se introduce

El valor de mω², en el control del mismo nombre
La energía total de la partícula E, en el control titulado Energía.

Se pulsa en el botón titulado Nuevo.

Observamos los valores de la energía cinética, potencial y la fuerza sobre la partícula, en particular, cuando la partícula pasa por el origen y por las posiciones de máximo desplazamiento.

m·ω²
Energía: