Péndulo de torsión
Procedimiento estático
Ya hemos estudiado el comportamiento de los muelles elásticos. La fuerza F que aplicamos es proporcional a la deformación del muelle, x.
F=kx
k se denomina constante elástica del muelle y se mide en N/m
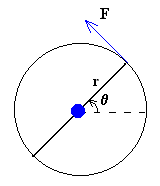
Para los muelles helicoidales existe una ley similar, la diferencia es que se aplica un momento en vez de una fuerza y la deformación es un desplazamiento angular.
F·r=Kθ
K se denomina constante de torsión y se mide en N·m
En el experimento real, se gira la varilla soporte un cierto ángulo θ, se mide con un dinamómetro la fuerza F que hay que aplicar a una distancia r del eje para que la varilla soporte se mantenga en equilibrio para dicho desplazamiento angular. Se ha de tener cuidado de que el eje del dinamómetro forme 90º con la varilla. Se desvía la varilla un ángulo mayor, se mide la fuerza F, situando el dinamómetro a la misma distancia r del eje, y así sucesivamente.
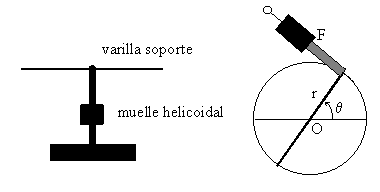
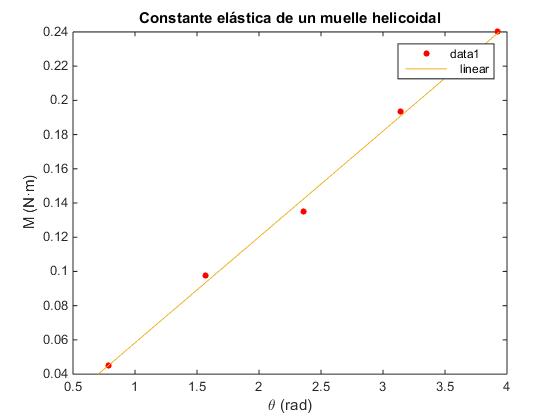
En una experiencia, se ha medido la fuerza F con un dinamómetro situado a r=15 cm del eje y formando 90º con la varilla para cada una de las posiciones angulares θ de la varilla 45º, 90º, 135º, 180º, 225º. A partir de estos datos, se le pide calcular la constante K del muelle helicoidal
| ángulo, θ | Fuerza(N) |
|---|---|
| 45 | 0.30 |
| 90 | 0.65 |
| 135 | 0.90 |
| 180 | 1.29 |
| 225 | 1.60 |
En un sistema de ejes se representa:
- M=F·d en N·m el eje vertical.
- El ángulo en radianes θ en el eje horizontal
Se calcula y se traza la recta que mejor ajusta a los datos cuya pendiente es la constante K del muelle helicoidal.
>> x=[45 90 135 180 225]*pi/180;
>> y=[0.30 0.65 0.90 1.29 1.60]*0.15;
>> plot(x,y,'ro','markersize',4,'markerfacecolor','r')
>> xlabel('\theta (rad)')
>> ylabel('M (N·m)')
>> title('Constante elástica de un muelle helicoidal')
En la ventana gráfica de MATLAB elegimos Tools/Basic fitting, activamos la casilla linear y obtenemos para la pendiente de la recta que mejor ajusta a los datos experimentales p1=0.061879. Por tanto la constante del muelle es K= 0.06 N·m
Procedimiento dinámico
En el procedimiento dinámico se separa la varilla soporte un cierto ángulo de su posición de equilibrio, se suelta y la varilla comienza a oscilar.
A partir de la medida del periodo de las oscilaciones se obtiene la constante elástica del muelle.
Cuando la varilla soporte se ha desviado un ángulo θ y se suelta el muelle ejerce sobre la varilla soporte un momento -Kθ. El momento es de sentido contrario al desplazamiento angular.
Tenemos un sólido en rotación alrededor de un eje fijo bajo la acción de un momento. La ecuación de la dinámica de rotación se escribe
Iα =-Kθ .
En forma de ecuación diferencial
Esta es la ecuación diferencial de un MAS de frecuencia angular ω 2=K/I y periodo
Ahora bien, el momento de inercia de la varilla soporte, del eje de rotación y del tornillo de sujeción no es conocido. Superamos este inconveniente, midiendo el periodo de las oscilaciones cuando la varilla tiene colocados dos cuerpos iguales de masa conocida, simétricamente dispuestos sobre la varilla.
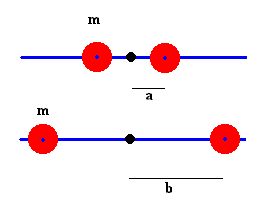
Cuando los cuerpos, en este caso cilindros, están a una distancia a del eje, el momento de inercia es
El último término de la suma, proviene de la aplicación del teorema de Steiner.
El periodo de las oscilaciones vale
Cuando los cuerpos están a una distancia b del eje, el momento de inercia es
El periodo de las oscilaciones vale
Restando los cuadrados de ambos periodos se eliminan las cantidades desconocidas Ivarilla e Icilindro
Midiendo Pa y Pb despejamos de la fórmula la constante de torsión del muelle helicoidal K.
En una experiencia se se han tomado los siguientes datos y a partir de ellos, se calcula la constante del muelle helicoidal K.
| Masa de cada una de los cilindros, m | 213 g |
| Posición a | 26 cm |
| Periodo a | 4.1 s |
| Posición b | 10 cm |
| Periodo b | 2.1 s |
| Constante de torsión K | 0.08 N·m |
|---|
Actividades
Se introduce
- Posición de a, en cm
- Posición de b, en cm
- Masa m de cada uno de los cilindros, en g
Se pulsa en el botón titulado Nuevo.
Se mide el periodo Pa de las oscilaciones del péndulo de torsión estando los cilindros en la posición a. Aparece activado el correspondiente botón de radio.
Se cambia los cilindros a la posición b, activando el botón de radio correspondiente. Se mide el periodo Pb de las oscilaciones del péndulo de torsión
Para que la precisión en la medidas sea mayor, se mide el periodo de varias oscilaciones y se divide el tiempo total entre el número de oscilaciones.
Práctica de laboratorio

Los datos de los equipos que disponemos en el laboaratorio son los siguientes:
| Masa de cada cilindro (kg) | 0.21 |
| Posición a (m) | 0.12 |
| Periodo a (s) | 2.3 |
| Posición b (m) | 0.26 |
| Periodo b (s) | 4.3 |
| Constante de torsión K (N·m) | 0.069 |
|---|
Sabiendo la constante K, nos disponemos a calcular los momentos de inercia I de tres cuerpos: el cilindro, el disco y la esfera. Compararemos con los resultados de aplicar las fórmulas de los momentos de inercia de estos cuerpos .

Cilindro
| Masa, m (kg) | 0.419 |
| Radio, R (m) | 0.05 |
| Momento de inercia calculado, mR2/2 (kg·m2) | 0.0005237 |
| Periodo P (s) | 0.58 |
| Momento de inercia medido (kg·m2) | 0.00059 |
Disco
| Masa, m (kg) | 0.2632 |
| Radio, R (m) | 0.1075 |
| Momento de inercia calculado, mR2/2 (kg·m2) | 0.00152 |
| Periodo P (s) | 0.87 |
| Momento de inercia medido (kg·m2) | 0.00132 |
Esfera
| Masa, m (kg) | 0.89 |
| Radio, R (m) | 0.069 |
| Momento de inercia calculado, 2mR2/5 (kg·m2) | 0.00169 |
| Periodo P (s) | 1.04 |
| Momento de inercia medido (kg·m2) | 0.00189 |

