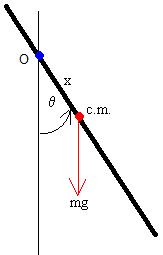
El péndulo compuesto es un sólido en rotación, alrededor de un eje fijo perpendicular a la varilla que pasa por O

La ecuación de la dinámica de rotación se escribe

I_O·α=-mgxsinθ

Donde x es la distancia entre el centro de masa y el centro de oscilación O.

I_O es el momento de inercia del cuerpo respecto del eje de rotación que pasa por O.

Cuando la varilla se separa un ángulo θ de la posición de equilibrio y se suelta, sobre el sólido actúa el momento del peso, que tiene signo contrario al desplazamiento.

Expresamos la ecuación de la dinámica de rotación en forma de ecuación diferencial

${\displaystyle \frac{d^2\theta }{d{t}^2}+\frac{mgx}{I_O}\sin \theta =0}$

Esta no es la ecuación diferencial de un Movimiento Armónico Simple. Si la amplitud es pequeña aproximamos el seno del ángulo al ángulo medido en radianes sinθ≈θ. La ecuación diferencial se escribe entonces

${\displaystyle \frac{d^2\theta }{d{t}^2}+\frac{mgx}{I_O}\theta =0}$

Esta es la ecuación diferencial de un M.A.S. de frecuencia angular ω y periodo P

${\displaystyle {\omega }^2=\frac{mgx}{I_O},P=2\pi \sqrt{\frac{I_O}{mgx}}}$

Por el teorema de Steiner

I_O=I_C+mx²=mR²+mx²

R se denomina radio de giro, para una varilla R²=l²/12, siendo l la longitud de la varilla. El periodo se escribe

${\displaystyle P=2\pi \sqrt{\frac{R^2+x^2}{gx}}}$

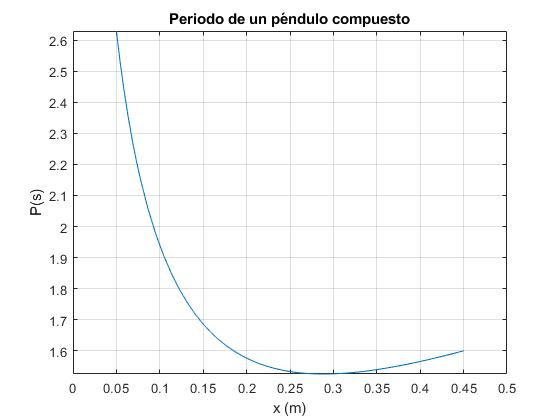
Cuando se representa P en función de x. Aparecen dos curvas simétricas con respecto a la posición de centro de masas. El periodo alcanza un valor infinito para x=0, es decir, cuando coincide el centro de masa con el centro de oscilación O. La curva presenta un mínimo para un cierto valor de x que se puede calcular derivando P respecto de x e igualando a cero.

${\displaystyle \frac{d{P}^2}{dx}=4{\pi }^2\frac{2g{x}^2-(R^2+x^2)g}{g^2{x}^2}=0,x_m=R,P_m=2\pi \sqrt{\frac{2R}{g}}}$

%péndulo compuesto de l=1 m de longitud
fplot(@(x) 2*pi*sqrt((1/12+x.^2)./(9.8*x)),[0.05,0.45])
xlim([0,0.5])
grid on
xlabel('x (m)')
ylabel('P(s)')
title('Periodo de un péndulo compuesto')

Actividades

Se mide el periodo de las oscilaciones para cada una de las posiciones del centro de oscilación.

El péndulo compuesto es una varilla de longitud l=1 m en la que se han hecho agujeros equidistantes 5 cm. El péndulo aparece oscilando en el primer agujero.

Se selecciona el centro de oscilación en el control Posición, se pulsa el botón titulado Nuevo

Momento de inercia y aceleración de la gravedad

Elevando al cuadrado la fórmula del periodo P del péndulo compuesto

${\displaystyle \frac{P^2}{4{\pi }^2}=\frac{R^2}{g}\frac{1}{x}+\frac{1}{g}x}$

Medimos el periodo P_i de péndulo para cada posición x_i, completando una tabla con N pares de datos

MATLAB nos permite ajustar los datos experimentales del cuadrado del periodo y=P²/(4π²) para cada posición x, a la función no lineal y=a/x+bx mediante la función nlinfit, alternativamente, se puede utilizar fminsearch

x=(5:5:45)/100;  
y=[2.620 1.936 1.668 1.568 1.520 1.512 1.536 1.576 1.600].^2/(4*pi^2); 
hold on
%representa los datos experimentales
plot(x,y,'bo','markersize',6,'markerfacecolor','b')
%modelo de función
f_ajuste =@(a,x) a(1)./x+a(2)*x;          
a0=[0.3 4];  %valor inicial de los parámetros
af=nlinfit(x,y,f_ajuste,a0)
%representa la función 
x=linspace(0.04,0.45,100);
y=f_ajuste(af,x);
plot(x,y,'r')
title('Péndulo compuesto')
xlabel('x (m)')
ylabel('P^2/(4·\pi^2)')
hold off   

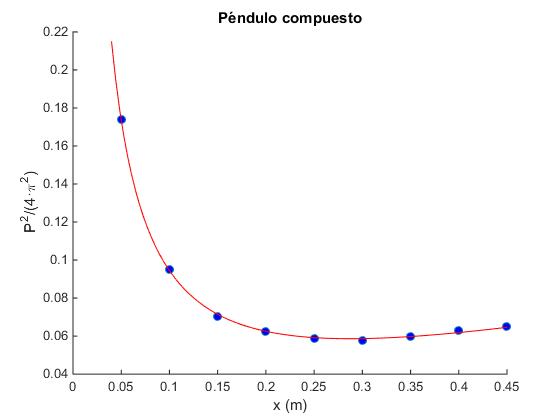
El valor de a es el primer elemento del vector af y el valor de b, el segundo elemento

af =    0.0084    0.1020

Los coeficientes a y b

${\displaystyle a=\frac{R^2}{g}=0.0084,b=\frac{1}{g}=0.102}$

La aceleración de la gravedad vale g=1/b=9.8 m/s². Conocida la aceleración de la gravedad g, obtenemos el momento de inercia del péndulo respecto de un eje que pasa por el centro de masas, mR²=0.0084·9.8·m=0.0823·m kg·m²

Fuerzas en el centro de oscilación

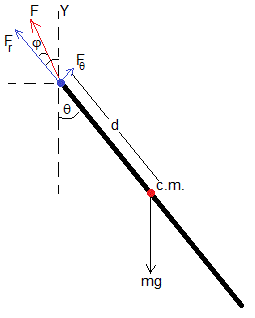
En el centro de oscilación actúa una fuerza F desconocida que forma un ángulo φ con la dirección radial (la que une el centro de oscilación con el centro de masa)

Ya hemos deducido al principio de esta página, la ecuación de la dinámica de rotación alrededor de un eje perpendicular que pasa por el centro de oscilación

${\displaystyle I_O\frac{d^2\theta }{d{t}^2}=-mgd\sin \theta }$

Tomando momentos respecto del centro de masa, la ecuación de la dinámica de rotación se escribe

${\displaystyle I_c\frac{d^2\theta }{d{t}^2}=-F\sin \phi ·d}$

I_c es el momento de inercia respecto de un eje perpendicular al plano de oscilación del péndulo que pasa por el c.m.. El teorema de Steiner relaciona los dos momentos de inercia.

${\displaystyle I_O=I_c+m{d}^2}$

Aplicamos la ecuación de la dinámica del movimiento circular uniforme, para describir el movimiento en la dirección radial, de forma similar al péndulo simple

${\displaystyle m{\left(\frac{d\theta }{dt}\right)}^{2}d=F\cos \phi -mg\cos \theta }$

Tomando el nivel cero de energía potencial en el centro de oscilación, el principio de conservación de la energía se escribe

${\displaystyle -mgd\cos {\theta }_0=\frac{1}{2}{I}_O{\left(\frac{d\theta }{dt}\right)}^2-mgd\cos \theta }$

Despejamos las componentes, Fcosφ y Fsinφ

${\displaystyle \begin{array}{l}F\sin \phi =\frac{I_c}{I_c+m{d}^2}mg\sin \theta \\ F\cos \phi =\frac{mg}{I_c+m{d}^2}\left\{\left(I_c+3m{d}^2\right)\cos \theta -2m{d}^2\cos {\theta }_0\right\}\end{array}}$

En el péndulo simple, solamente tenemos componente en la dirección radial, la tensión de la cuerda

Las componentes rectangulares de la fuerza F en el centro de oscilación son

• Horizontal, F_x

${\displaystyle \begin{array}{l}{F}_x=-F\sin (\theta -\phi )=F\cos \phi \sin \theta -F\sin \phi \cos \theta =\\ -\frac{mg}{I_c+m{d}^2}\left\{\left(I_c+3m{d}^2\right)\cos \theta -2m{d}^2\cos {\theta }_0\right\}\sin \theta -\frac{I_c}{I_c+m{d}^2}mg\sin \theta \cos \theta =\\ =-\frac{m{d}^2}{I_c+m{d}^2}mg\left\{\left(3\cos \theta -2\cos {\theta }_0\right)\sin \theta \right\}\end{array}}$

• Vertical, F_y

${\displaystyle \begin{array}{l}{F}_y=F\cos (\theta -\phi )=F\cos \phi \cos \theta +F\sin \phi \sin \theta =\\ \frac{mg}{I_c+m{d}^2}\left\{\left(I_c+3m{d}^2\right)\cos \theta -2m{d}^2\cos {\theta }_0\right\}\cos \theta +\frac{I_c}{I_c+m{d}^2}mg{\sin }^2\theta =\\ =\frac{m{d}^2}{I_c+m{d}^2}mg\left\{\left(3\cos \theta -2\cos {\theta }_0\right)\sin \theta +\frac{I_c}{m{d}^2}\right\}\end{array}}$

La componente F_x es similar al péndulo simple salvo el factor de escala que multiplica al peso mg. La componente F_y es similar al péndulo simple salvo el factor de escala que multiplica al peso y el término adicional I_c/(md²)

• Representamos $\frac{F_x}{mg}\frac{I_c+m{d}^2}{m{d}^2}$, el término proporcional a F_x entre corchetes, en función de θ para varias amplitudes

hold on
for th=[30,60,90,120,150,179]*pi/180 %amplitudes
    fplot(@(x) -(3*cos(x)-2*cos(th)).*sin(x),[-th,th],
'displayName',num2str(th*180/pi))
end
hold off
legend('-DynamicLegend','location','best')
xlabel('\theta')
ylabel('F_x')
grid on
title('Componente F_x')



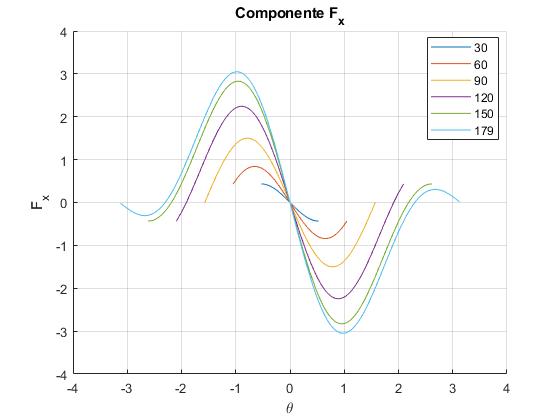
• Representamos $\frac{F_y}{mg}\frac{I_c+m{d}^2}{m{d}^2}-\frac{I_c}{m{d}^2}$, el término proporcional a F_y sin el término constante, en función de θ para varias amplitudes

hold on
for th=[30,60,90,120,150,179]*pi/180 %amplitudes
    fplot(@(x) (3*cos(x)-2*cos(th)).*cos(x),[-th,th],
'displayName',num2str(th*180/pi))
end
hold off
legend('-DynamicLegend','location','best')
xlabel('\theta')
ylabel('F_y')
grid on
title('Componente F_y')

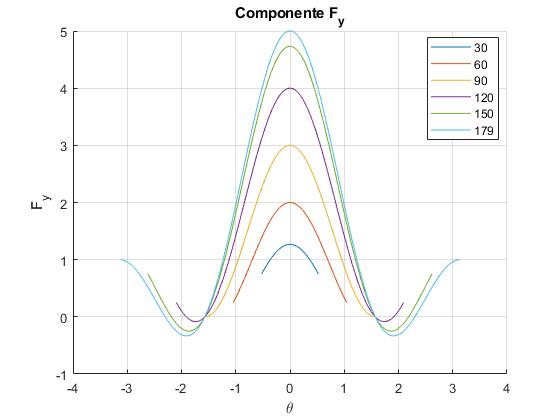
El lector interesado, puede estudiar en detalle estas funciones, máximos, mínimos y los puntos de corte con el eje horizontal, es decir, los ángulos para los cuales la componente F_x se anula

Referencias

Peter F Hinrichsen. Compound pendulum pivot force. Eur. J. Phys. 42 (2020) 025001