Elektromagnetismoa

Autoindukzioa 
eta elkar-indukzioa

Autoindukzioa.
R-L zirkuitua

Zirkuitu akoplatuak (I)

Zirkuitu akoplatuak (II)

Oszilazio elektrikoak

Kondentsadore-
bikotearen problema

K. alternoko zirkuitu
baten elementuak

Sistema elektro-
mekaniko oszilatzailea

Eraztun baten auto-
indukzioa neurtzea

LCR zirkuitua seriean
Erresonantzia

Argiaren abiadura 
hutsean neurtzea

Faraday-ren legearen
efektu mekanikoak

Thomson-en eraztuna (I)

Thomson-en eraztuna (II)

Ekuazio diferentzialaren soluzioak

Kondentsadoreen kargak amaieran

Energiaren analisia

Zirkuitu erreal baten portaera

Saiakuntza

Erreferentzia

Kondentsadoreen elkarketak orrian adibide bat aztertzen da: kondentsadore bi paraleloan konektatuta, biak C kapazitate berekoak. Hasierako egoeran bietako batek Q karga du eta bestea deskargatuta dago, eta amaierako egoeran biek dute karga bera: Q/2 alegia. Kondentsadoreetan metatutako energia kalkulatzen bada frogatzen da, amaierako egoeran, energia justu hasierakoaren erdia dela.

Energia-galera hori justifikatzeko, zirkuituan kondentsadore bi eta erresistentzia bat dagoela suposatzen da. Energia-galera guztia erresistentzian gertatu da bero gisa, Joule efektuaz. Azalpen honek sinesgarria dirudi, kondentsadore bien arteko edozein kablek R erresistentzia duelako baina, hala ere, zirkuituaren autoindukzioak badu zerikusia.

Korrontea hasieran,  t<0 denean, i=0 balio du. Eta bat-batean, konexioa burutzean,  t=0 aldiunean alegia, i₀=Q/(RC) balio du. Hortaz, intentsitateak jarraitasun-eza dauka, eta horren arrazoia da, edozein zirkuituk ere L autoindukzioa baduela eta ez dugula kontutan hartu. Azter dezagun bada efektu guztiekin.

Kondentsadore bi, erresistentzia bat eta autoindukzio batez osatutako zirkuitua

Kontsidera dezagun ondoko irudian erakusten den zirkuitua: C₁ eta C₂ kondentsadoreak, R erresistentzia eta L autoindukzioa.

Hasierako egoeran 1 kondentsadoreak Q karga osoa du eta 2 kondentsadorea deskargatuta dago, eta zirkuitua etenda dago. Halako batean, t=0 aldiunean, zirkuitua ixten da, 1 kondentsadorea deskargatzen hasten da eta 2 kondentsadorea ordea, kargatzen.

Bitarteko t aldiune batean honakoa betetzen da:

• C₁ kondentsadoreak  q₁ karga du.
• C₂ kondentsadoreak  q₂ karga du.
• R erresistentzian zehar i intentsitatea zirkulatzen ari da.
• L autoindukzioan zehar i intentsitatea zirkulatzen ari da.

Neur ditzagun potentzial-diferentziak ondoko puntu guztien artean: a-b, b-c, c-d, eta d-a.

Zirkuitua itxita dagoenean honakoa betetzen da:

V_ab+V_bc+V_cd+ V_da =0

• C₁ kondentsadorean a puntuko potentziala (xafla negatiboa) b puntukoa baino baxuagoa da (xafla positiboa), beraz, V_ab= -q₁/C₁
• R erresistentzian korronteak zirkulatzen du b-tik c-rantz, beraz V_bc= iR
• C₂ kondentsadorean c puntuko potentziala (xafla positiboa) a puntukoa baino altuagoa da (xafla negatiboa), beraz, V_cd=q₂/C₂
• Autoindukzioan intentsitatea handitzen ari bada indar elektroeragilea handitzearen aurka doa:  V_da=Ldi/dt.

Zirkuitu osoaren ekuazioa hau da:

Eta edozein aldiunetan q₁+q₂=Q.  Gainera, hasierako egoeran 2 kondentsadorea bada deskargatuta dagoena eta 1 kondentsadorea kargatuta dagoena, q₁ gutxitzen joango da eta q₂ handitzen, beraz intentsitatea (karga-garraioa denbora unitateko):

Ekuazio osoa berridatz daiteke  q₂-ren menpe:

edo bestela,

Ekuazio diferentzial horren soluzioa honelakoa da:

y₁ konstantea soluzio partikularra da eta gainerakoa soluzio orokorra, hain zuzen oszilazio indargetuetan agertzen dena.

y₁ soluzio partikularra ekuazio diferentzialean ordezkatuz honakoa lortzen da:  y₁=QC₂/(C₁+C₂)

Hasierako baldintzen arabera A eta B kalkula daitezke: q₂=0, eta dq₂/dt=0.

Egiaztatzen da, hasieran, t=0 unean, q₂=0 eta  i=0. Eta denbora luzea iragan ondoren, t→∞,  i→0 eta

Beste dedukzio osagarri bat

Zirkuitu osoaren ekuazioa denborarekiko deribatzen bada

Geratzen den ekuazioa oszilazio indargetuena da:

Ekuazio diferentzial hori integratzeko hasierako baldintzak ezagutu behar dira: t=0 aldiunean, i intentsitatea eta bere lehen deribatua di/dt.

Gure kasuan hasierako baldintzak honakoak dira: t=0 unean intentsitatea i=0, C₁ kondentsadorearen karga q₁=Q, eta C₂ kondentsadorearen karga nulua q₂=0. Zirkuitu osoaren ekuazioa hasierako aldiunean:

Ekuazio diferentzialaren soluzioak

Ekuazio diferentzialaren soluzioa, bi parametroen araberakoa da: g eta w_o .

Oszilazio indargetuak (g<w₀)

Hasierako baldintzen arabera A anplitudea eta φ hasierako fasea kalkulatzen dira:

Oszilazio indargetuen ekuazioa hau da:

Oszilazio kritikoa (g=w₀)

Kasu honetan ekuazio diferentzialaren soluzioa honelakoa da:

Hasierako baldintzen arabera A eta B konstanteak kalkulatzen dira:

Eta i intentsitatearen adierazpena denboraren menpe honela geratzen da:

Oszilazio gain-indargetua (g>w₀)

Kasu honetan ekuazio diferentzialaren soluzioa honelakoa da:

Hasierako baldintzen arabera A eta B konstanteak kalkulatzen dira:

Eta i intentsitatearen adierazpena denboraren menpe honela geratzen da:

Kondentsadoreen kargak amaieran

Hasierako baldintzak ezagunak dira, (t=0, C₁ kondentsadorearen karga q₁=Q, eta C₂ kondentsadorearena q₂=0) eta kondentsadore bakoitzaren karga denboraren menpe kalkula daiteke:

Denbora nahikoa iragan ondoren (teorikoki infinitu) oreka-egoera atzemango da, baina kondentsadoreen karga kalkulatzeko ez da beharrezkoa kasu bakoitzeko integrazio-prozesu osoa burutzea. Horren ordez, oreka-egoerako baldintza ordezka daiteke: i zerorantz doa eta bere deribatua ere bai di/dt . Hona zirkuitu osoaren ekuazioa, oreka-egoeran:

-q₁/C₁+q₂/C₂=0.

Eta karga osoa kontserbatu behar denez:

q₁+q₂=Q

Orduan:

Energiaren analisia

Hasieran energia osoa C₁ kapazitateko kondentsadorean baino ez dago:

Eta amaieran, oreka egoeran (teorikoki denbora infinituan),  energia kondentsadore bietan banatuta dago:

Energia-galera, U_f-U_i, da, R erresistentzian bero gisa barreiatu dena:

Emaitza hau berau, alegia R erresistentzian barreiatutako energia, egiazta daiteke ere integralen kalkulu osoa burutzen:

• Oszilazio indargetuak:

Zatika integratzen. Azken adierazpenera iristeko ordezkatu behar da:

• Oszilazio gain-indargetuak:

Sinu hiperbolikoaren terminoa ordezkatuz, sinh(βt)=(exp(βt)-exp(-βt))/2 , karratura berretuz, gero bider exp(-2γt) bidertuz, integrala berehalakoa geratzen da. Baina azken adierazpeneraino iristeko, kontuan izan behar da: 

• Oszilazio kritikoak

Aldagai aldaketa egin behar da: x=2γt, eta geratzen den integrala funtzio ezaguna da, gamma funtzioa alegia, eta integralen tauletan azaltzen da:

Azken emaitzaraino iristeko kontuan izan behar da:  γ=ω₀

Zirkuitu erreal baten portaera

Intentsitatearen portaera hiru parametroen menpekoa da:  R, L eta C.

Demagun esate baterako zirkuitu bat 5 cm-ko erradioduna, kobrezko kableez konektatua, eta kableek 0.5mm-ko erradioa dutela.

Kableen erresistentzia hau da:

Autoindukzioa ondoko formulaz kalkula daiteke:

D zirkuituaren diametroa da eta d kablearen diametroa.

Kondentsadore biak berdinak badira eta euren kapazitatea adibidez C₁=C₂=100μF, orduan frekuentzia angeluar propioa edo naturala honakoa izango da:

Eta indargetze-koefizientea

Kasu honetan  γ/ω₀<<1. Beraz oszilazio indargetuen kasuan gaude eta ontzi komunikatuen kasuan suposatzen den antzera jokatuko dugu:

Kondentsadore biak berdinak badira C₁=C₂=C, eta indargetze txikiaren baldintza betetzen da, alegia γ<<ω₀,  orduan oszilazio indargetuaren frekuentzia ia oszilazio askeen frekuentzia naturalaren berdina da ω≈ω₀

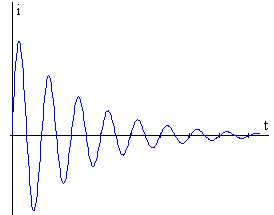	Honelako emaitza lortzeko oszilazio indargetuen applet-ean honako baldintzak idatzi behar dira: Indargetze-koefizientea, 7.0 Posizioa, 0.0 Abiadura, 500
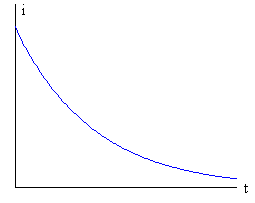	Zirkuituaren autoindukzioa kontutan hartu gabe bestelako emaitza hau lortzen da: Emaitza horretan intentsitatea denborarekin gutxituz doa eta esponentzialki.

Saiakuntza

Idatzi:

• Kapazitatea 1 laukian, lehen kondentsadorearen C₁ kapazitatea, hasieran kargatuta dagoena, μF-tan.

• Kapazitatea 2 laukian, bigarren kondentsadorearen C₂ kapazitatea, hasieran deskargatuta dagoena, μF-tan.

• Zirkuituaren R erresistentzia miliohmetan (mΩ).

• Zirkuituaren L autoindukzioa mikroHenrytan (μH).

• Adierazpen grafikoaren denbora-eskala ere alda daiteke Eskala laukian ematen diren aukerak erabilita.

Hasi botoia sakatu.

Kondentsadore batetik bestera karga pasatuz zirkuituak oszilatzen du, likido batek ontzi komunikatuetan egiten duen bezalaxe. Karga-fluxua (korrontearen intentsitatea) puntu gorriez adierazten da.

Kondentsadore bakoitzaren karga-kopuruak oszilatzen du baina, denbora pasa ahala, balio limite konstante baterantz jotzen du, R erresistentzia nulua ez bada behintzat.

Grafikoaren ardatz bertikalean kondentsadore bien karga adierazten da, q₁/Q eta q₂/Q  eta ardatz horizontalean t denbora mikrosegundotan, μs.

Adibidea:

Idatz bedi

• Kapazitateak: C₁=3·10^-6 F, C₂=2·10^-6 F

• Erresistentzia R=50·10^-3 Ω

• Autoindukzioa L=2·10^-6 H

Kalkulatzen da

• Indargetze-koefizientea  γ=12500 s^-1

• Maiztasun angeluar naturala, ω₀=645497 rad/s

• Maiztasun angeluar indargetua ω=645377 rad/s

Maiztasun biak ia berdinak dira.

Kalkula ditzagun kargak, t=100·10^-6 s unean:

• C₂ kondentsadorean karga,  q_2/Q = 0.41

• eta C₁ kondentsadorean,  q₁/Q = 1-q₂/Q = 0.59

Hemen Q , hasierako kargari deitu zaio, t=0 unekoa alegia.

Denbora 'infinitua' iragan ondoren kondentsadore bietako kargak konstante mantentzen dira:

• q₂/Q=0.4

• q₁/Q=0.6