Solido zurruna

Momentu angeluarra
kontserbatzen

Disko bi akoplatzen (I)

Disko bi akoplatzen (II)

Indar zentral bat
hagatxo batean

Patinatzaile bat biraka

Aurrez aurreko talka
elastikoaren analogia

Pendulu balistikoa (II)

Kutxa bat irauli

Talka inelastikoa: bala
eta disko biratzailea

Hagatxo batez
abiadura transmititzen

Kontserbazioak:
momentu lineala eta 
momentu angeluarra

Disko-horma talka

Diskoa-diskoa talka (I)

Diskoa-diskoa talka (II)

Multzoaren egoera hasieran eta amaieran

Hasierako egoeratik amaierako egoerara

Saiakuntza

Erreferentziak

Partikula biren aurrez-aurreko talkak aztertzen direnean (dimentsio bakarrean) bi talka-mota bereizten dira: talka elastikoak eta inelastikoak. Bietan kontserbatzen da momentu lineal totala, baina talka elastikoetan bakarrik kontserbatzen da partikulen energia zinetiko totala.

Orri honetan dispositibo bat aztertzen da, momentu angeluarraren kontserbazioaren adibide, baina gainera erakusten du, disko baten energia zinetikoa nola transferi dakieken oso-osorik bi partikulari.

Demagun irudiko diskoa: M masa eta R erradioa, eta bere zentroaren inguruan bira dezake. Partikula bi, m masadunak, soka banarekin lotuta daude diskoaren zentrora, sokak ertzeko bi koskatan tolesten dira. Irudian sokak gorriak dira eta aldiz, koskak urdinak. Diskoa biraka hasten da eta, halako batean, partikulak askatu egiten dira zulotxotik, baina sokekin lotuta segitzen dute. Soken luzera (l+R) da, diskoaren zentrotik neurtuta, irudiak erakusten duen bezala. Azkenean, sokak zuzendu egiten dira, baina zentroan lotuta jarraitzen dute (ikusi amaierako saiakuntza).

Talka elastikoak aurrez aurre

Demagun aurrez aurreko talka elastikoa partikula biren artean. Esaterako, bietako bat geldi dago, u₂=0

1. Momentu linealaren kontserbazioa:

m₁u₁ =m₁v₁+m₂v₂

2. Energia zinetikoaren kontserbazioa:

Ekuazio biko sistema da, eta esaterako, ezagutzen badira, partikula mugikorraren abiadura talkaren aurretik (u₁) eta partikula bien masak (m₁ eta m₂), kalkula daitezke partikulen abiadurak talkaren ondoren (v₁ eta v₂). Hona hemen emaitzak:

Partikulen masen erlazioaren arabera, talkaren ondoren, lehen partikula:

• Geldi gera daiteke, baldin m₁=m₂ bada.

• Hasierako noranzko berean mugi daiteke, baldin m₁>m₂ bada.

• Hasierako noranzkoaren aurka mugi daiteke, baldin m₁<m₂ bada.

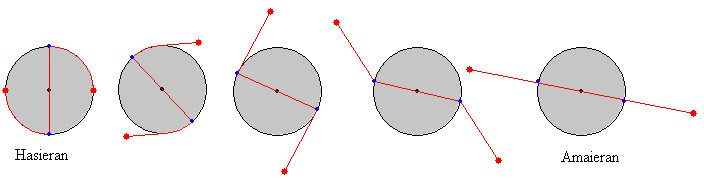
Multzoaren egoera, hasieran eta amaieran

Hasieran, diskoak biratu egiten du abiadura angeluar konstanteaz eta partikula biak itsatsita ditu zulotxoetan. Bat batean, partikulak zulotxoetatik askatzen dira, eta diskotik urrutiratzen doaz eta, beraz, diskoaren errotazioaren abiadura angeluarra gutxituz doa. Amaieran, sokek erabat zuzen bukatzen dute, alegia, ez dituzte jadanik koskak ukitzen, eta abiadura angeluar konstanteaz biratzen segitzen dute, hasierako noranzko berean, baina diskoaren abiadura angeluarrak honako hiru egoerak izan ditzake:

• Abiadura angeluar konstantea du hasierako noranzko berean.

• Geldi geratzen da.

• Abiadura angeluar konstantea atzematen du, baina aurkako noranzkoan.

Sekzio honetan aztertuko ditugu hasierako eta amaierako egoerak soilik, eta ondorengo sekzioan aztertuko da, zehazkiago, batetik bestera doan denbora-tartea.

Hasierako egoera

Partikula biak diskoaren ertzean lotuta daude. Partikulen masa m da, diskoaren masa M eta erradioa R, eta hasierako abiadura angeluarra ω₀.

• Multzoaren momentu angeluar totala,

• Eta E energia totala:

Amaierako egoera

Alde batetik, diskoak biratu egiten du ω_d abiadura angeluarraz eta, bestetik, partikula biek higidura zirkularra dute, ω_p abiadura angeluarraz eta l+R erradioaz.

• Multzoaren L momentu angeluar totala

• Eta E energia totala:

Kanpo-indarrak dira, ardatzak egiten dituen erreakzioak, beraz, momentu erresultantea ardatzarekiko nulua da: M_k=0. Hortaz, L momentu angeluarra konstantea da. Barne-indarrek ere ez dute lanik egiten (partikulak lotzen dituen soka luzaezina delako, ez-elastikoa) eta hortaz, energia ere kontserbatzen da.

Momentu angeluarraren kontserbazioa eta energiaren kontserbazioa idazten badira, ekuazio biko sistema lortzen da, justu talka elastikoaren modukoa:

Ezagutzen badira hasierako abiadura angeluarra eta masa guztiak, orduan kalkula daitezke amaierako abiadura angeluarrak:

• Partikulen abiadura angeluarra (ω_p) beti da positiboa.

• Diskoaren abiadura angeluarra (ω_d)  positiboa, negatiboa edo nulua izan daiteke.

Esaterako, ω_d  nulua izateko honako baldintza bete behar da: c²a²=abc(a+b-c), eta hortik bakan daiteke b.

b²-b(c-a)-ca=0

Soluzio bat negatiboa da (ez du esangura fisikorik) eta bestea positiboa: b=c, edota bestela idatzita:

Baldintza hori betetzen bada, partikulak askatzean, diskoa gelditu egingo da: ω_d=0

• Erlazio horretan m da, partikulen masa.

• M, diskoaren masa.

• R, diskoaren erradioa.

• (R+l) sokaren luzera, diskoaren zentrotik neurtuta.

Hasierako egoeratik amaierako egoerara

Ondoko irudiak erakusten ditu higiduraren zati ezberdinak, hasieratik amaierara arte. Atal honetan aztertuko ditugu zehazkiago:

Partikulak euren zulotxoetatik askatzen diren unean, indar zentrifugoak diskoaren ertzetik urrutiratu egiten ditu, eta espiral baten moduko ibilbidea jarraitzen dute.

Azter dezagun partikula baten posizioa bitarteko aldiune batean: une horretan, partikula dago r distantziara diskoaren zentrotik, eta θ angelua osatzen du erreferentziazko X ardatzarekin (koordenatu polarrak), ezkerreko irudiak erakusten duen bezala. Beste partikula justu aurkako posizioan dago. Partikularen vp abiadura deskonposa daiteke bi osagaitan: bata erradiala, vr, eta bestea tangentziala: vθ=r·ωp. Hemen, vr=dr/dt eta vθ=r·dθ/dt. Diskoaren abiadura angeluarra une horretan ωd da.

• Egoera horretan, momentu angeluar totala honela adieraz daiteke:

    (1)

• Eta energia totala:

       (2)

Higiduraren lehen atala

Partikula askatu ondoren, hasieran, sokaren zati bat aske dago airean, baina beste zati batek oraindik diskoaren ertza ukitzen du. Aske dagoen soka-zatia zuzena da eta diskoaren ertza ukitzen dagoen zatia zirkularra da. Dei diezaiogun D sokaren zati biak elkartzen diren puntuari. D puntuaren abiadura, hain zuzen, R·ω_d da. Lor dezagun erlazio bat abiadura horren eta P puntuaren v_p abiaduraren artean. Horretarako, proiekta ditzagun bi abiadurak P eta D puntuak lotzen dituen norabidean.

R·ω_d=r·ω_p·sinδ-v_r·cosδ,   (3)

eta hemen sinδ=R/r

Orduan hiru ekuazio dauzkagu eta hiru ezezagun:

• partikularen abiaduraren bi osagaiak: erradiala v_r=dr/dt, eta tangentziala v_θ=r·ω_p=r·dθ/dt

• diskoaren abiadura angeluarra.

Lehen eta hirugarren ekuazioetatik ω_p eta ω_d bakan daitezke r eta v_r-ren menpe. Hona hemen emaitzak:

ω_p eta ω_d-ren bi adierazpen horiek ordezka daitezke bigarren ekuazioan eta ekuazio hori garatuz eta sinplifikatuz, honako emaitza lor daiteke: v_r(r):

Kalkulatu nahi duguna da partikulen posizioa (r,q) denboraren menpe. Lehenik, r kalkulatzeko, azken ekuazio diferentzial hori ebatzi behar da, lehen ordenakoa. Ondoren, r ezagututa, q  kalkulatzeko beste ekuazio diferentzial bat ebatzi behar da: ω_p=dθ/dt , hori ere lehen ordenakoa. Ekuazio biak lehen ordenakoak dira eta prozedura numerikoez ebatz daitezke:

Aurreko irudiaren ezkerreko aldean ikusten da, diskoaren diametroaren posizio angeluarra erlazionatuta dagoela partikularen posizio angeluarrarekin (q) (irudian hartu da  l=πR/2, baina edozein luzera izan daiteke). Hona hemen diskoaren diametroaren posizio angeluarra:

θ+(π/2-δ)+φ.

Izan ere, PD eta O puntuek hiruki zuzena osatzen dute, eta beraz (ikusi irudiaren eskumako aldean):

	Hasierako egoera Hasierako aldiunean, t=0, partikularen posizioa da, θ=0, eta r=R. Hasierako baldintza horiekin vr=0, eta orduan kalkulu numerikoa ez da abiatzen. Ondorengo simulazioan kalkulua abiatzeko, honako baldintzak hartzen dira hasieran:  t=0, θ=0, eta r=R+ΔR. Kalkuluan, ΔR txikia hartu da, izan ere, R-ren milarena.
	Amaierako egoera Soka erabat askatzen da eta ez du jadanik diskoaren ertza ukitzen, koskatxoa izan ezik. Une horretan, sokaren bi zatiak perpendikularrak dira, beraz: r2=R2+l2 edota bestela esanda tanδ=R/l, edota φ=0.

Higiduraren bigarren atala

Soka osorik askatzen denean diskoaren ertzetik, jadanik sokaren bi zatiak zuzenak dira, justu D puntuan tolestuta. D puntuaren abiadura hau da: R·ω_d . Kalkula dezagun P puntuaren v_p abiadura baldintza berri horietan. Horretarako, proiekta ditzagun P puntuaren eta D puntuaren abiadurak P eta D puntuak lotzen dituen norabidean. Bi puntuak lotuta daudenez, abiadura horiek berdinak izan behar dira:

R·ω_d·cosf=r·ω_p·sinδ-v_r·cosδ,   (3)

Erlazio horretan f angelua da, sokak osatzen duena diskoaren ertzaren tangentearekin

POD hirukian, sinuaren eta kosinuaren teoremak aplika daitezke:

Higiduraren bigarren zati honetan, berriz ere hiru ekuazio ditugu eta hiru ezezagun. Lehenengo bi ekuazioak, lehen bezala, momentu angeluarraren eta energiaren kontserbazioak dira. Ezezagunak ere hiru:

• partikularen abiaduraren bi osagaiak: erradiala v_r=dr/dt, eta tangentziala v_θ=r·ω_p=r·dθ/dt

• diskoaren abiadura angeluarra: ω_d

Lehen eta hirugarren ekuazioetatik ω_p eta ω_d bakan daitezke, r eta v_r-ren menpe adierazita.

Adierazpen horiek, ω_p eta ω_d , ordezka daitezke bigarren ekuazioan eta ekuazio hori garatuz eta sinplifikatuz, honako emaitza lortzen da v_r(r):

Kalkulatu nahi duguna da partikulen posizioa (r,q) denboraren menpe. Lehenik, r kalkulatzeko, azken ekuazio diferentzial hori ebatzi behar da, lehen ordenakoa. Ondoren, r ezagututa, q  kalkulatzeko beste ekuazio diferentzial bat ebatzi behar da: ω_p=dθ/dt , hori ere lehen ordenakoa. Ekuazio biak lehen ordenakoak dira eta prozedura numerikoez ebatz daitezke:

Goiko irudian ikusten da, diskoaren diametroaren posizio angeluarra erlazionatuta dagoela partikularen posizio angeluarrarekin (q). Hona hemen diskoaren diametroaren posizio angeluarra:

θ+π-(π/2+f+δ)= θ+π/2-f-δ

Eta,

Hasierako egoera

Higiduraren bigarren atalaren hasierako egoera da, higiduraren lehen atalaren amaierakoa, alegia, soka eta diskoaren diametroa elkarren perpendikularrak direnean. t=t₀ aldiunean, partikulatik diskoaren zentrora dagoen distantzia hau da: r²=R²+l², eta θ₀ angelua osatzen du X ardatzarekin.

Amaierako egoera

Sokak erabat zuzen daude, eta diskoaren diametroaren norabide bera dute. Une horretan, diskoaren ω_d abiadura angeluarra konstante bilakatzen da, eta partikulek ibilbide zirkularra dute, (R+l) erradioduna eta ω_p abiadura angeluar konstantea.

Adibideak

• Partikulen masak, m=0.07 kg, bakoitzak.

• Diskoaren masa, M=1.0 kg

• Diskoaren erradioa, R=0.5 m

• Sokaren luzera, (R+l)=R+πR/2, beraz, l=0.785 m

• Diskoaren hasierako abiadura angeluarra, ω₀=1 rad/s

Momentu angeluarra:

Energia totala:

Amaierako egoeran, diskoaren abiadura angeluarra ω_d da, partikulek ibilbide zirkularra dute, l+R=1.285 m, erradioduna eta ω_p abiadura angeluarra dute.

Plantea ditzagun momentu angeluarraren eta energiaren kontserbazioak:

Hona hemen, ezezagun bi eta ekuazio biko sistemaren emaitzak:

ω_d= -0.227 rad/s eta ω_p=0.815 rad/s

2 adibidea:

Bada partikulen masa kritiko bat, diskoa geldirik uzten dutena:

Egiazta dezagun:

Momentu angeluar totala:

L=0.1473 kgm²/s

Energia totala:

E=0.0736 J

Plantea ditzagun momentu angeluarraren eta energiaren kontserbazioak, eta lortuko ditugu diskoaren eta partikulen abiadura angeluarrak, ω_d eta ω_p.

Hona hemen, sistemaren emaitzak:

ω_d=0.0 rad/s eta ω_p=1.0 rad/s

Egiazta  bedi beste adibide bat. Partikulen masa honakoa bada: m=M/π=1.0/π=0.3183 kg, orduan diskoaren errotazioaren noranzkoa aldatu egiten da amaierako egoeran.

Saiakuntza

Aukeran idatz daiteke:

• Partikularen masa, m  kg-tan, desplazamendu-barrari saguaz eragiten.

Eta gainontzeko parametroak finkotzat hartu dira:

• Diskoaren masa: M=1.0 kg

• Diskoaren erradioa: R=0.5 m

• Sokaren luzera (R+l), eta hartu den balioa hau da: (R+πR/2) beraz, l= πR/2=0.785 m

• Diskoaren hasierako abiadura angeluarra: ω₀=1 rad/s.

Hasi botoia sakatu.

Diskoa mugitzen hasten da, eta ikusten da, nola doazen partikulak diskotik urruntzen. Amaieran, sokak erabat zuzendu dira eta partikulek ibilbide zirkularra jarraitzen dute soketan lotuta abiadura angeluar konstanteaz, eta diskoa ere abiadura angeluar konstanteaz mugitzen da. Leihatilaren ezkerreko aldean bi barra-diagramek adierazten dituzte energia zinetikoak eta momentu angeluarrak (diskoarenak urdinez eta partikulenak gorriz). Ikusten denez, bai energia zinetiko totala eta baita momentu angeluar totala ere konstanteak dira, baina diskoaren energia eta momentu angeluarra partikuletara transferitzen doa, eta alderantziz ere, diskoak alderantzizko noranzkoaz biratzen amaitzen duen kasuan.

Leihatilaren eskumako aldean, eta uneoro, idatziz ematen dira hainbat datu: lehenik, partikulen posizio erradiala (r) eta angeluarra (q), eta abiadura angeluarra (w_p). Bigarrenik diskoaren posizioa (angelua) eta abiadura angeluarra (w_d). Eta azkenik, multzo osoaren momentu angeluarra (L) eta energia (E).