Solido zurruna

Solido zurrun baten momentu angeluarra

Steiner-en teorema

Errotaziozko energia zinetikoa

Errotazioaren dinamikaren ekuazioa

Momentu angeluarraren kontserbazio-printzipioa

Lana eta energia errotazio-higiduran

Bulkada angeluarra

Partikula baten momentu angeluarra

Partikula baten momentu angeluarra puntu batekiko honela definitzen da: posizio-bektorearen (r) eta momentu linealaren (mv) arteko biderketa bektoriala: L=r´mv

Solido zurrun baten momentu angeluarra

Solido zurrun batek ardatz finko baten inguruan biratzen duenean, solidoa osatzen duten partikulek zirkunferentziak deskribatzen dituzte (ikusi ondorengo irudia). Zirkunferentzia guztien zentroak errotazio-ardatzean kokatuta daude eta partikula baten abiadura bere zirkuluaren erradioaren proportzionala da:

v_i =w ×r_i      edo      v_i=w ·R_i

Partikula guztiek w abiadura angeluar bera dutenez, ardatzetik hurbil dauden partikulek v_i abiadura txikiagoa dute, eta ardatzetik urruti daudenek berriz, handiagoa. Irudian, errotazio-ardatza Z ardatza da.

Har dezagun solidoa osatzen duen partikula bat: mi masa du, ri posizio-bektorea O puntuarekiko, eta Ri erradiodun zirkunferentzia bat deskribatzen ari da vi abiaduraz. Partikularen momentu angeluarra Li da, O puntuarekiko, irudiak erakusten duena, eta honako modulua du: Li=rimivi Li momentu angeluarrak ez du Z ardatzaren norabidea, baina bere Z osagaia hau da: Liz=miviricos(90-q i), hau da,

Solidoa osatzen duten partikula guztien momentu angeluar totala O puntuarekiko hau da:

Eta momentu angeluar totalaren Z osagaia:

Parentesiaren barruko terminoari "inertzia-momentu" deritzo:

Orokorrean, momentu angeluar total bektoreak (L) ez du izaten errotazio-ardatzaren norabide bera (w-ren norabide bera), baina posiblea da, esaterako, solidoa simetrikoa denean errotazio-ardatzarekiko. Orduan, L-ren x eta y osagaiak nuluak dira eta Lz da osagai bakarra. Ondorioz, w eta L bektoreak paraleloak dira, alboko irudian bezala. Hori gertatzen denean errotazio-ardatzari "inertziazko ardatz nagusi" deritzo. Kasu horretan, alegia, errotazio-ardatza "nagusia" denean, badago erlazio sinple bat L momentu angeluarraren eta w abiadura angeluarraren artean: Lz=Iw        edota           L=Iw

Solido baten inertzia-momentua ez da kantitate finko bat, masa edo bolumena bezalakoa, aldiz, inertzia-momentua errotazio-ardatzaren arabera aldatzen da. Inertzia-momentua minimoa da errotazio-ardatza masa-zentrotik pasatzen denean.

Steiner-en teorema

Solido baten inertzia-momentua ezagutzen bada, bere masa-zentrotik pasatzen den edozein ardatzekiko, orduan, Steiner-en teoremari esker, solido horren inertzia-momentua kalkula daiteke aurreko ardatzaren paraleloa den beste edozein ardatzekiko.

O puntutik pasatzen den ardatzarekiko inertzia-momentua hau da:

Eta C masa-zentrotik pasatzen den ardatzarekiko inertzia-momentua hau da:

I_O eta I_C erlazionatzeko r_i eta R_i erlazionatu behar dira:

Irudiak erakusten du:

Bigarren ataleko bigarren terminoa nulua da, masa-zentroaren posizioa delako (x_C) masa-zentrotik ikusita.

Adibideak

Demagun hagatxo bat, M masa eta L luzeraduna, eta hagatxoaren alde banatan esfera bi, m masa eta r erradiodunak, eta biak hagatxoaren zentrotik d distantziara. Steiner-en teorema erabiliz, kalkula dezagun gorputz horren inertzia-momentua, zentrotik pasatzen den ardatz perpendikularrarekiko:

Pendulu batek hagatxo bat du, M masa eta L luzeraduna, eta bere muturrean disko bat kokatu da, m masa eta r erradioduna. Steiner-en teorema erabiliz, kalkula dezagun pendulu horren inertzia-momentua O tik pasatzen den eta pantailarekiko perpendikularra den ardatzarekiko:

Errotaziozko energia zinetikoa

Solido baten partikulek zirkuluak deskribatzen dituzte, zirkuluen zentroa errotazio-ardatzean dago eta partikulen abiadurak zirkuluen erradioen proportzionalak dira: v_i=w ·R_i . Solidoaren energia zinetiko totala izango da, partikula guztien energia zinetikoen batura. Batura hori, sinplifikazioak egin ondoren, inertzia-momentuaren eta abiadura angeluarraren menpekoa geratzen da soilik:

Errotazioaren dinamikaren ekuazioa

Solidoa partikula-multzo bat ere bada. Partikula-multzoen errotazioaren dinamika gogoratuz, partikula bakoitzak jasaten duen indarra bi zatitan bana daiteke: batetik, kanpo-indarrek eragiten diotena eta bestetik, multzoko gainontzeko partikulek eragiten diotena. Har dezagun bi partikulaz osaturiko multzoa. 1 partikulak jasaten dituen indarrak bi dira: F₁ kanpo-indarra eta 2 partikulak eragiten diona, F₁₂. Aldiz, 2 partikulak jasaten dituen indarrak ere bi dira: F₂ kanpo-indarra eta 1 partikulak eragiten diona, F₂₁.

Esaterako, bikote hori Lurra eta Ilargia balira, kanpo-indarrak izango lirateke Eguzkiak eragiten dizkienak (eta gainontzeko planetek). Barne-indarra ordea, elkarri eragiten dioten erakarpena izango litzateke.

Partikula bakoitzerako betetzen da, bere momentu angeluarraren aldakuntza denborarekiko dela, jasaten ari den indar totalaren momentua:

Ekuazio bi horiek gehitzen baditugu, atalez atal, gero, aplikatzen badugu biderketa bektoriala banakorra dela baturarekiko, eta azkenik, Newton-en hirugarren legea gogoratzen badugu (F₁₂= −F₂₁) honakoa lortzen da:

Baina honako bektore biak paraleloak dira: r₁-r₂ eta F₁₂. Beraz, euren arteko biderketa bektoriala nulua da. Hortaz, geratzen den ekuazioa hau da:

Partikula-multzoaren L momentu angeluar totalaren deribatua denborarekiko eta kanpo-indarren M_k momentu erresultantea berdinak dira.

Gatozen berriz ere solido zurruna aztertzera. Demagun solidoa ardatz "nagusi"  baten inguruan biraka ari dela. Orduan, bere momentu angeluarra hau da: L=I·w. Eta aurreko ekuazioa honela berridatz daiteke:

Partikula-multzo baten momentu angeluarra

Har dezagun berriz ere lehengo irudiko partikula-bikotea. Bere momentu angeluar totala, koordenatuen jatorriarekiko, hau da:

L=r₁´ m₁·v₁+r₂´ m₂·v₂

Berridatz ditzagun posizioak eta abiadurak, baina oraingoan, masa zentroarekiko:

r_1mz=r₁ -r_mz
r_2mz=r₂ -r_mz

v_1mz=v₁-v_mz
v_2mz=v₂-v_mz

Ordezkatzen baditugu momentu angeluarraren adierazpenean:

L=(r_1mz+r_mz) ´ m₁·(v_1mz+v_mz)+ (r_2mz+r_mz) ´ m₂·(v_2mz+v_mz)=

(r_1mz ´ m₁·v_1mz)+ (r_2mz ´ m₂·v_2mz)+ r_mz´ (m₁·v_1mz+ m₂·v_2mz)+ (m₁·r_1mz+ m₂·r_2mz) ´ v_mz

Baina masa-zentroaren posizioak eta abiadurak honako baldintzak betetzen dituzte:

m₁·v_1mz+ m₂·v_2mz=0,
m₁·r_1mz+ m₂·r_2mz=(m₁+m₂)·r_mz

Beraz:

L=L_mz+(m₁+m₂)·r_mz ´ v_mz

Orokorrean, edozein partikula-multzotan, bere masa totala m bada:

Lehen terminoa barne-momentu angeluarra da, alegia, partikulek dutena masa zentroarekiko, eta bigarrena kanpo-momentu angeluarra da, alegia, masa-zentroak duena koordenatuen jatorriarekiko.

Kanpo-indarren momentua, M_k, eta barne momentu angeluarra, L_mz: zein erlazio dute.

Partikula-bikote batek jasaten duen kanpo-indarren momentuak koordenatuen jatorriarekiko, bi atal ditu:

M_k= r₁´F₁+r₂´ F₂=(r_1mz+r_mz) ´ F₁+(r_2mz+r_mz) ´ F₂= r_1mz´ F₁+r_2mz´ F₂+ r_mz´ (F₁+F₂)= M_mz+ r_mz´ (F₁+F₂).

Lehen terminoa da, kanpo-indarren momentua masa-zentroarekiko eta bigarrena da, F₁+F₂ kanpo-indar erresultantearen momentua masa-zentroan aplikatuta egongo balitz bezala.

Momentu angeluarra, L, deribatzen bada denborarekiko:

Bigarren terminoa, bi bektore paraleloren biderketa bektoriala da, beraz nulua, eta masa-zentroaren higidura ekuazioa gogoratuz:

honela berridatz daiteke:

Baina aurreko atalean frogatu dugunez:

Orduan honako erlazioa lortzen da:

Azken emaitza hori eta aurrekoa (dL/dt=M_k) berdinak dira, baina interpretazio ezberdinak dituzte.

Aurrekoan aipatzen den momentu angeluarra (L) eta indarren momentua (M_k) biak definitzen dira koordenatuen O jatorri finkoarekiko, alegia erreferentzia-sistema inertzial batena. Azken horrek ordea, aipatzen dituen momentu angeluarra (L_mz) eta indarren momentua (M_mz) biak definitzen dira masa-zentroarekiko, eta masa-zentroak ez du zertan geldi egon, izan ere, azeleratua izan daiteke.

Azken erlazio hori oso erabilgarria da solido zurrunaren higidura deskribatzeko masa-zentroaren inguruan.

Azter dezagun zehazkiago erlazio hori:

Hemen A edozein puntu izan daiteke, L_A partikula-multzoaren momentu angeluarra A puntuarekiko, eta M_A kanpo-indarren momentu totala puntu berarekiko.

Dei diezaiogun "i" partikularen posizioari koordenatuen jatorriarekiko, ri . Dei diezaiogun "i" partikularen posizioari A puntuarekiko, riA . Irudiak bi bektore horien erlazioa erakusten du. ri=rA+riA "i" partikularen abiadura erreferentzia-sistema inertzialarekiko vi, da eta A puntuaren abiadura vA.

Partikula-multzoaren momentu angeluarra A puntuarekiko, L_A , hau da:

Dei diezaiogun F_i "i" partikulak jasaten duen kanpo-indarrari. Newton-en bigarren legearen arabera:

Eta kanpo-indar totalaren momentua A puntuarekiko:

Masa zentroaren posizioa , r_mz , honela definitzen da:

Hemen M da, partikula-multzoaren masa totala, eta orduan kanpo-indar totalaren momentua honela berridatz daiteke:

Erlazio bera lortzen da L_A momentu angeluarra deribatzen badugu denborarekiko:

bigarren terminoa, M(r_mz-r_A)×a_A , baliogabetzen bada, orduan honako erlazio sinplifikatua betetzen da: M_A=dL_A/dt . Noiz baliogabetzen da bigarren termino gehigarri hori?

• A puntua masa-zentroa bera denean: r_mz=r_A

• A puntuaren azelerazioa nulua denean: a_A =0, hau da, A puntua abiadura konstantez mugitzen denean (erreferentzia-sistema inertzial baten jatorria izan daiteke).

• A puntuaren azelerazioa, a_A, honako bektorearekiko paraleloa denean: (r_mz-r_A), hau da, A-ren azelerazioa masa-zentrorantz doanean.

Solido zurrunaren Higidura Orokorra aztertzen dugunean, adibide guztietan honakoa erabiliko dugu:

solido zurrunaren momentu angeluarra, L_mz , eta kanpo-indarren momentuak, M_mz , biak kalkulatuko dira masa-zentroarekiko.

Momentu angeluarraren kontserbazio-printzipioa

Momentu angeluarraren kontserbazio-printzipioa ondorio zuzena da: kanpo-indarren momentu totala (M_k) nulua bada, orduan solidoaren momentu angeluarra (L) konstantea izango da:

Kanpo-indarren momentu totala nulua izateak (M_k=0) ez du esan nahi kanpo-indar erresultantea nulua izan behar denik (F_k=0), eta alderantziz, kanpo indar erresultantea nulua izateak (F_k=0) ez du esan nahi kanpo indarren momentu totala nulua izan behar denik (M_k=0).

Lana eta energia errotazioan

Partikularen dinamikan frogatzen da, indar erresultantearen lana eta partikula horren energia zinetikoaren aldakuntza berdinak direla.

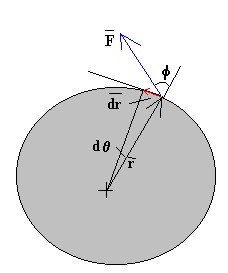Har dezagun solido zurrun bat, irudiak erakusten duen bezala biratzen ari dena, ardatz finko baten inguruan. Demagun kanpo-indar bat aplikatzen zaiola, F, solidoaren P puntu batean. Solidoak dt denbora-tarte txiki batean dq  angelua biratzen du, eta beraz P puntua desplazatu egin da: dr=rdq . Orduan, F indarrak egindako lan infinitesimala honela idatz daiteke: dW = F ·dr = F sinf ·rdq

F·sinf , aplikatutako F indarraren osagai tangentziala da, izan ere, desplazamenduaren norabideko osagaia. Indar horren osagai erradialak ez du lanik burutzen, desplazamenduarekiko perpendikularra delako.

Izan ere, F indarraren momentua da, indar horren osagai tangentziala bider ardatzerainoko r distantzia. Hortaz, indar horrek egindako lana honela ere berridatz dezakegu:

Eta solidoak angelu finitu bat biratu badu, lan totala honela kalkulatzen da:

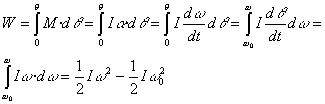
Frogaketa horretan errotazioaren dinamikaren ekuazioa erabili da, alegia, M=Ia , eta baita ere, abiadura angeluarraren eta azelerazio angeluarraren definizioak.

Lortu dugun emaitza hori partikula baten lana-energia teoremaren antzekoa da: solido bati eragiten dioten indarren momentu totalak (M_k), solidoaren errotaziozko energia zinetikoa aldatzen du (Iw²/2).

Bulkada (edo inpultsu) angeluarra

Partikularen dinamikan bulkada (edo inpultsu) linealaren kontzeptua jorratzen da. Partikula bati indar erresultanteak denbora batez eragiten badio, partikularen momentu lineala aldatzen da:

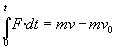
Solido biratzaile baten kasuan, bulkada "angeluarra" modu analogoan definitzen da.

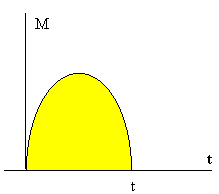Ardatz finko baten inguruan biratzen ari den solido bati aplikatzen zaizkion indarren momentu totalak (Mk), t denbora batez irauten badu, solidoaren momentu angeluarra (Iw) honenbeste aldatzen da :