| Orri honetan berriz ere aztertuko dugu disko biren
arteko talka, baina oraingoan sei ezezaguneko eta sei ekuazioko sistema
ebatzi beharrean, adierazpen matematikoak lortzen saiatuko gara:
- Bi diskoen abiadurak talkaren ondoren: v1 eta v2.
- Bi diskoen norabideek talkaren ondoren osatzen dituzten angeluak,
f1 eta f2,
talkaren unean bi zentroak lotzen dituen zuzenarekiko.
- Bi diskoen abiadura angeluarrak talkaren ondoren:
w1
eta w2.
- Talkan galdutako energia: Q.
Datu gisa hartuko ditugu bi parametro: bata, lehen diskoaren u1
abiadura talka baino lehen, eta bestea, abiadura horrek osatzen duen θ1
angelua, talkaren unean bi zentroak lotzen dituen zuzenarekiko. Zuzen horri
X ardatza deituko diogu, eta angelu guztiak berarekiko adieraziko ditugu.
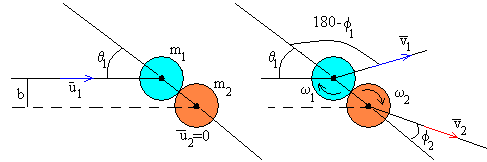
Irudiak erakusten ditu gainera, diskoen masak (m1 eta m2)
eta erradioak (r1 eta
r2). Bigarren diskoa geldi dago talka baino lehen (u2=0)
eta lehenak u1 abiadura du. Talka-parametroa da, lehen
diskoaren zentroaren abiaduraren norabidetik bigarren diskoaren zentrora
dagoen distantzia (b), baina θ1 angeluaz
finkatua dago.
Talkaren ondoren, lehen diskoaren abiadura v1
da eta f1 angelua osatzen du X
ardatzarekiko, eta aldi berean biraka ari da
w1
abiadura angeluarraz, bere zentrotik pasatzen den ardatz
perpendikularrarekiko. Bigarren diskoak, talkaren ondoren, v2
abiadura du, f2 angelua osatzen
du X ardatzarekiko eta w2
abiadura angeluarraz biratzen du bere zentrotik pasatzen den ardatz
perpendikularrarekiko.
Datutzat hartzen dira:
- Bi diskoen masak, m1 eta m2
eta erradioak, r1 eta r2
- Talka baino lehen, bigarren diskoa geldi dago, u2=0.
Lehen diskoaren abiadura u1 da eta bere
norabidea θ1, lehen esan bezala, X ardatzarekiko.
Ezezagunak sei, denak talkaren ondorengoak:
- Lehen diskoaren zentroaren abiadura, v1,
norabidea f1, eta
errotazioaren abiadura angeluarra: w1.
- Bigarren diskoaren zentroaren abiadura, v2,
norabidea f2, eta
errotazioaren abiadura angeluarra: w2.
Talka-parametroa
Talka-parametroa honela definitzen da: lehen diskoaren zentroaren
abiaduraren norabidetik bigarren diskoaren zentroraino dagoen distantzia (b).
Izan ere, talka parametroa ezagututa, θ1 angelua
finkatuta geratzen da, ondoko irudiak erakusten duen bezala (θ1
angelua da, talkaren unean bi zentroak lotzen dituen zuzenak lehen diskoaren
zentroaren abiaduraren norabidearekin osatzen duena.)
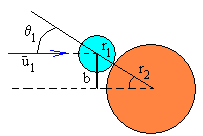 |
b=(r1+r2)·sinθ1 |
- Bi diskoek multzo isolatu bat osatzen dute, kanpo-indar erresultantea
nulua baita. Beraz, momentu lineal totala kontserbatzen da:
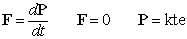
Esan bezala, X ardatza deritzogu talkaren unean bi diskoen zentroak
lotzen dituen zuzenari, eta beraz, Y ardatza norabide horrekiko
perpendikularrari.
Irudian u1, v1
eta v2 bektoreak, adierazi dira euren osagaien
menpe, X eta Y ardatzean zehar:
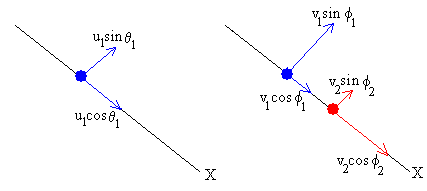
- Momentu lineala Y ardatzean:
m1u1·sinq1=m1v1·sinf1+m2v2·sinf2
(1)
m1u1·cosq1=
m1v1·cosf1+m2v2·cosf2
(2)
- Disko bakoitzak jasaten duen indar erresultantea, izan ere, talkaren
indarra da, eta justu P kontaktu-puntuan aplikatzen da. Beraz, P
puntuarekiko, disko bakoitzaren momentu angeluar indibiduala ere
konstantea izango da:
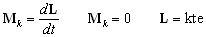
Lehen diskoan:
m1·r1·u1sinq1=m1·r1·v1sinf1+I1w1
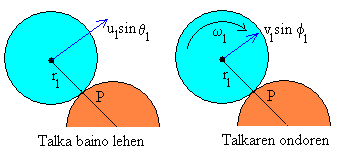
Eta bigarren diskoan:
0= -m2·r2·v2sinf2+I2w2
Diskoak direnez, hona hemen euren inertzia-momentuak zentrotik pasatzen
den ardatzarekiko:

Beraz:
r1w1 =2·u1sinq1-2·v1sinf1 (3)
r2w2 =2·v2sinf2
(4)
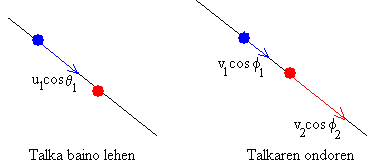
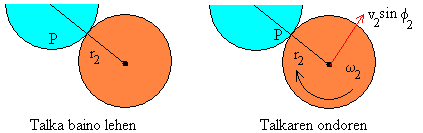
Hona hemen
itzultze-koefizientearen definizioa:
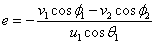
e ·u1cosq1=
-v1cosf1+v2cosf2
(5)
Guztira, 6 ezezagun ditugu eta 5 ekuazio soilik, beste ekuazio bat
gehiago behar da arazoa osorik ebazteko. Azter dezagun disko biek elkarri
egiten dioten indarra justu kontaktuan daudenean.
Hasteko, diskoen arteko indarrak ezagut ditzagun:
- Bi diskoen arteko indar normalak diskoen elastikotasunaren
menpekoak dira; indar tangentzialak aldiz, diskoen arteko
marruskadura-indarraren menpekoak dira, eta beraz, bi gainazalen
egoeraren menpekoak.
- Bai itzultze-koefizientea eta baita marruskadura-koefizientea ere
konstanteak dira, eta materialen ezaugarrien menpekoak dira soilik.
Kasu bi gerta daitezke:
Ez dute irristatzen

Diskoek P kontaktu-puntuan eta talkaren ondoren ez badute irristatzen,
orduan bi diskoen abiadurak P puntuan berdinak izan behar dira:
v1sinf1-r1
w 1=v2sinf2+r2
w2
(6)
Irristatzen dute
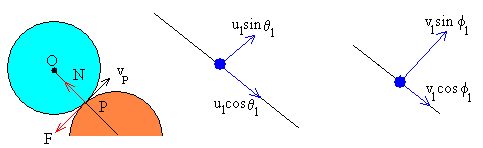
Lehen diskoak jasaten dituen indarrak bi dira:
- N, erreakzio normala, diskoaren zentrorantz.
- F, marruskadura-indarra, P puntuaren abiaduraren aurka.
N erreakzio normalak lehen diskoari momentu linealaren X osagaia
soilik aldatzen dio, irauten duen
Dt denbora-tarte txikian.
Inpultsoa kalkulatzen badugu:
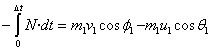
Era berean, F indarraren inpultsoak lehen diskoaren momentu
linealaren Y osagaia aldatzen dio soilik:
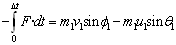
Baina irristatzen badu, orduan N eta F erlazionatuta daude: F=m ·N,
eta beraz inpultsoak ere bai:
m ·(v1cosf1-
u1cosq1)=
(v1sinf1-u1sinq1)
(6')

bigarren diskoak jasaten dituen indarrak ere bi dira:
- N, erreakzio normala, diskoaren zentrorantz.
- F, marruskadura-indarra, P puntuaren abiaduraren aurka.
Indar bi horiek eta lehen diskoak jasaten dituenak berdinak eta aurkakoak
dira.
N erreakzio normalak bigarren diskoari momentu linealaren X
osagaia soilik aldatzen dio. Hona hemen
inpultsoa:
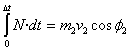
Era berean, F indarraren inpultsoak momentu linealaren Y osagaia
aldatzen dio soilik, eta F indarraren noranzkoa P puntuaren
abiaduraren aurkakoa da.
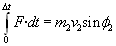
Eta N eta F erlazionatuta daude: F=m ·N,
eta beraz inpultsoak ere bai:
m ·v2cos
f2= v2sinf2
tanf2 =m
(7')
Sei ezezagun dauzkagu eta bost ekuazio, aztertu ditugun bi
kasuetan balio dutenak:
m1u1·sinq1=m1v1·sinf1+m2v2·sinf2 (1)
m1u1·cosq1=
m1v1·cosf1+m2v2·cosf2
(2)
r1w1 =2·u1sinq1-2·v1sinf1
(3)
r2w2 =2·v2sinf2
(4)
e·u1cosq1=
-v1cosf1+v2cosf2
(5)
Irristatzen badu
- (7') ekuazioak berak bakarrik f2
angelua ematen du, alegia bigarren diskoaren zentroaren v2
abiadurak X ardatzarekin osatzen duen angelua:
tanf2 =m
(7')
(7') ekuazio hori bestela ere berridatz
daiteke:
sinf2 =m
·cosf2
(7')
- Nola kalkulatu lehen diskoaren v1 abiadura eta
f1 angelua: (7') ekuazioa (1) ekuazioan
ordezkatu eta ondoren bakandu (5) ekuazioan v2cosf2
eta ordezkatu (2) ekuazioan:
u1·(m1sinq1-m
·e·m2cosq1)=m1v1·sinf1+m2v1·m
·cosf1
u1·(m1-m2 ·e)·cosq1=
(m1+m2)v1·cosf1
Dei diezaiogun M=m1/m2, eta bakan
dezagun (2) ekuazioan v1·cosf1
eta (1) ekuazioan v1·sinf1
:
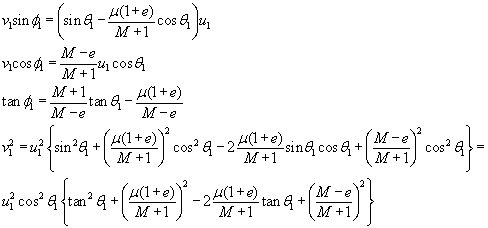
- Nola kalkulatu bigarren diskoaren v2
abiadura:
(5) ekuazioan bakan bedi v1·cosf1
eta ordezka bedi (2) ekuazioan:
m1u1·cosq1=
m1v1·cosf1+m2v2·cosf2
(2)
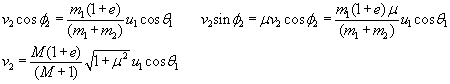
- Bi diskoen errotazioen abiadura angeluarrak:
w1 eta w2
Bakan bedi (1) ekuazioan v1·sinf1 eta
ordezka bedi (3) ekuazioan:
r1w1 =2·u1sinq1-2·v1sinf1=2(m2/m1)v2·sinf2
(3)
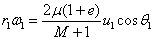
r2w2 =2·v2sinf2
(4)
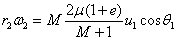
Egiaztatzea
Orain arte ez dugu (6) ekuazioa erabili, baina egiazta daiteke betetzen
dela:
m ·(v1cosf1-
u1cosq1)= v1sinf1-u1sinq1
(6')
Ordezka bitez, lehen bakandutako v1cosf1
eta v1sinf1
eta ekuazioa betetzen dela egiaztatzen da.
Energiaren
balantzea
Kalkulatzen badira energia
zinetikoak talkaren ondoren eta talkaren aurretik, euren arteko diferentzia
talkaren Q energia-galera da.
Talkaren ondoren, disko
bakoitzaren energia zinetikoa kalkulatzeko translazioa eta errotazioa gehitu
behar dira, baina talka baino lehen lehen diskoak translazio hutsa du:
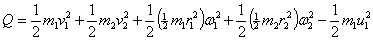
Talkaren ondoren lortutako abiadurak
ordezkatzen baditugu (v1, v2,
w1 eta w2)
orduan, energia-galeraren ekuazio osoa geratzen da hasierako baldintzen
menpe idatzita (u1 eta θ1):
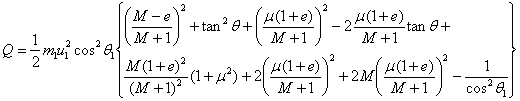
Ekuazio hori sinplifika daiteke honako erlazio trigonometrikoak erabiliz: sin2θ1=2sinθ1·cosθ1
eta 1+tan2θ1=1/cos2θ1
. Zenbait buruketaren ondoren honako emaitza lortzen da:
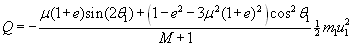
Ez badu irristatzen
- Nola kalkulatu bigarren diskoaren v2
abiadura eta f2
norabidea:
Bakan bitez (3) eta (4) ekuazioetan r1w1
eta
r2w2 , eta
ordezka bitez (6) ekuazioan:
r1w1 =2·u1sinq1-2·v1sinf1
(3)
r2w2 =2·v2sinf2
(4)
v1sinf1-r1
w1=v2sinf2+r2
w2
(6)
Ordezkatu ondoren, honelako adierazpena lortzen da:
3v1sinf1-2·u1sinq1=3v2sinf2
Eta ekuazio horretan bakan daiteke v1sinf1
eta (1) ekuazioan ordezkatu:
m1u1·sinq1=m1v1·sinf1+m2v2·sinf2
(1)
(m1/3)u1·sinq1=(m1+m2)v2·sinf2
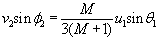
Ondoren (5) ekuazioan bakan bedi v1cosf1
eta ordezka bedi (2) ekuazioan:
m1u1·cosq1=
m1v1·cosf1+m2v2·cosf2
(2)
e·u1cosq1= -v1cosf1+v2cosf2
(5)
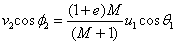
Ekuazio bi horiek ematen dituzte bigarren diskoaren v2
abiadura eta f2
norabidea talkaren ondoren:
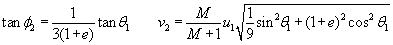
- Nola kalkulatu lehen diskoaren v1 abiadura eta f1
norabidea:
(1) ekuazioan ordezka bedi v2·sinf2
eta bakan bedi v1·sinf1
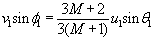
Orduan, (2) ekuazioan ordezka bedi v2·cosf2
eta bakan bedi v1·cosf1
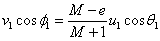
Ekuazio bi horiek ematen dituzte lehen diskoaren v1
abiadura eta f1
norabidea talkaren ondoren:
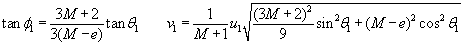
- Bi diskoen errotazioen abiadura angeluarrak:
w1 eta w2
(3) eta (4) ekuazioetan ordezka bitez lehenago bakandutako v1sinf1
eta v2sinf2 :
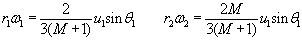
Energiaren
balantzea
Lehen bezala, kalkulatzen
badira energia zinetikoak talkaren ondoren eta talkaren aurretik, euren
arteko diferentzia talkaren Q energia-galera da. Talkaren ondoren,
disko bakoitzaren energia zinetikoa kalkulatzeko translazioa eta errotazioa
gehitu behar dira, baina talkaren aurretik lehen diskoak translazio hutsa
du:
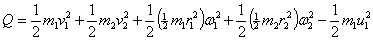
Talkaren ondoren lortutako abiadurak
ordezkatzen baditugu (v1, v2,
w1 eta w2)
orduan, energia-galeraren ekuazio osoa geratzen da hasierako baldintzen
menpe idatzita (u1 eta θ1):
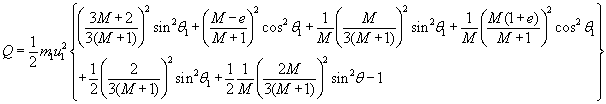
Eta zenbait sinplifikazio eginez honako adierazpena lortzen da:
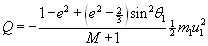
Kasu berezia: Aurrez-aurreko talkak.
Talka-parametroa nulua denean, b=0, orduan θ1
angelua ere nulua da: θ1=0. Talka-mota horri
aurrez-aurreko deritzo:
- Talkaren ondoren bi diskoen abiadurek X ardatzarekin osatzen dituzten
angeluak, biak nuluak dira: f1=0
eta f2 =0.
- Bi diskoen errotazioen abiadura angeluarrak ere nuluak dira:
w1=0 eta w2 =0.
- Bi diskoen zentroen abiadurak:

Izan ere, ekuazio horiek eurak lortzen dira partikulen arteko
aurrez aurreko talkak aztertzean eta bigarren partikula geldi dagoenean
talka baino lehen: u2=0
. Kasu horretan definitzen bada M=m1/m2.
Orduan, hona hemen talkan galdutako energia:
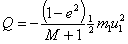
izan ere, lehen diskoak talka baino lehen duen
energia zinetikoaren (1-e2)/(M+1)
zatia galtzen da.
Angelu kritikoa
Konpara ditzagun diskoen
f1 eta f2 angeluak
talkaren ondoren, aztertu ditugun bi kasuetan:
tanf2
=m
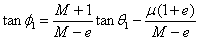
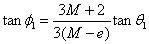
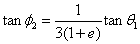
tanθc=3(1+e)μ
Eta orduan
f1 eta
f2 angeluen
adierazpenak honakoak dira kasu bietan:
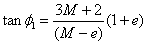
tanf2
=m
-
Baldin θ1<θc
bada, orduan, bi diskoek talka egitean ez dute irristatzen, eta
kasu horri dagozkion ekuazioak erabili behar dira.
-
Aldiz, θ1>θc
baldin bada, orduan bi diskoek talka egitean irristatzen
dute, eta beraz, kasu horri dagozkion ekuazioak erabili behar dira.
Laborategian errazago neurtzen da b talka-parametroa, θ1
angelua baino baina, lehen esan bezala, biak erlazionatuta daude:
b=(r1+r2)·sinθ1
Eta
f1 eta
f2 angeluak baino
errazago neurtzen dira φ1
eta φ2 , hots, v1 eta v2
abiadurek osatzen dituzten angeluak, baina
lehen diskoaren eraso-norabidearekiko, irudiak erakusten duen bezala:
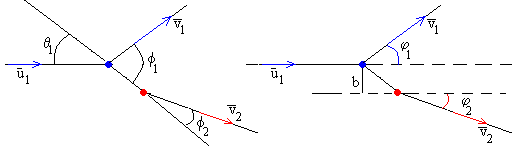
Hona hemen angelu horien arteko erlazioak:
φ1=f1
-θ1
φ2=θ1-f2
1 adibidea: Diskoen datuak:
- Demagun M=m1/m2=1 alegia bi diskoen masak
berdinak direla.
- Diskoen erradioak: r2=1 eta r1=1.
- Bi diskoak altzairuzkoak dira: e=0.94 eta m
=0.10
Talka baino lehen:
- Lehen diskoaren hasierako abiadura: u1=3.5
- Talka-parametroa: b=1.5.
Talka-parametroa ezagututa, θ1 angelua kalkula
daiteke:
1.5=(1+1)·sinθ1
θ1 =48.6º Eta irristatzearen angelu kritikoa hau da: tanθc=3(1+0.94)0.1
θc=30.2º
Beraz, kasu berezi honetan bi diskoek elkar ukitzean irristatzen dute.
Talkaren ondoren:
- Lehen diskoaren v1 abiadura eta f1
norabidea:
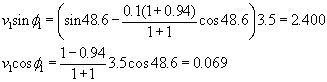
v1=2.40,
f1=88.3º
Eta laborategian neurtutako angelua: φ1=88.3 - 48.6=39.7º
(horizontalaren gainetik)
- Bigarren diskoaren v2 abiadura eta f2
norabidea:
tanf2
=0.1
f2
=5.7º
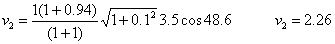
Eta laborategian neurtutako angelua: φ2=48.6 - 5.7=42.9º
(horizontalaren azpitik)
- Bi diskoen errotazioen abiadura angeluarrak:
w1 eta w2
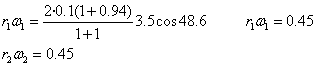
(Berdinak ateratzen dira, eta biak positiboak, beraz, erlojuaren orratzen
alde)
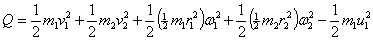
Q= -0.594
Bestela ere kalkula daiteke:
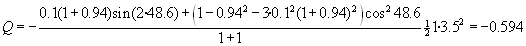
2. adibidea: Diskoen datuak:
- Demagun m1=0.5 eta m2=1.
- Diskoen erradioak: r2=1 eta r1=2.
- Bi diskoak altzairuzkoak dira: e=0.94 eta m
=0.10
Talka baino lehen:
- Lehen diskoaren hasierako abiadura: u1=3.5
- Talka-parametroa: b=0.4.
Talka-parametroa ezagututa, θ1 angelua kalkula
daiteke:
0.4=(2+1)·sinθ1
θ1 =7.7º Eta irristatzearen angelu kritikoa hau da: tanθc=3(1+0.94)0.1
θc=30.2º
Beraz, kasu berezi honetan bi diskoek elkar ukitzean ez dute irristatzen.
Talkaren ondoren:
- Bigarren diskoaren v2 abiadura eta f2
norabidea:
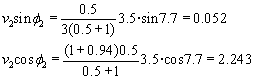
v2=2.244
f2 =1.3
Eta laborategian neurtutako angelua: φ2=7.7-1.3=6.4º
(horizontalaren azpitik)
- Lehen diskoaren v1 abiadura eta f1
norabidea:
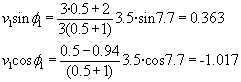
v1=1.080
f1 =160.4º
Eta laborategian neurtutako angelua: φ1=160.4-7.7=152.7º
(horizontalaren gainetik)
- Bi diskoen errotazioen abiadura angeluarrak:
w1 eta w2
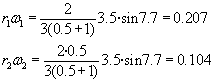
(Biak positiboak dira, erlojuaren orratzen alde)
- Talkan galdutako energia:
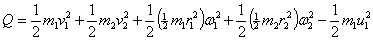
Q= -0.246
Eta bestela kalkulatuta:
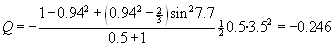
Saiakuntza
Ondoko taulan zenbait materialen itzultze- eta marruskadura-koefizienteak
ematen dira:
| Materialak |
Itzultze-koef. e |
Marruskadura-koef.
m |
| Altzairua-altzairua |
0.94 |
0.10 |
| Aluminioa-aluminioa |
0.61 |
0.12 |
| Letoia-letoia |
0.57 |
0.11 |
| Altzairua-letoia |
0.65 |
0.10 |
| Aluminioa-letoia |
0.55 |
0.10 |
| Altzairua-aluminioa |
0.62 |
0.09 |
Iturria: Doménech A, Doménech M.T. Colisiones inelásticas de
esferas. Revista Española de Física 4, 3 (1990) 52-56 orrialdeak.
Aukeran idatz daitezke:
- Lehen diskoaren masa, m1, dagokion kontrolean
idatziz (bigarren diskoaren masa finkotzat hartu da, m2=1)
- Lehen diskoaren erradioa, r1 dagokion
kontrolean idatziz (bigarren diskoaren erradioa finkotzat hartu da,
r2=1)
- Bi diskoen materialak, zerrenda tolestuan bikote bat
aukeratuta. Bikotea aukeratu ondoren marruskadura- eta itzultze-
koefizienteak finkatuta geratzen dira, eta beheko laukietan erakusten
dira.
- Lehen diskoaren hasierako abiadura, talka baino lehen, u1
, dagokion kontrolean idatziz.
- Bigarren diskoa hasieran geldirik dago.
- Talka-parametroa, b, dagokion kontrolean idatziz:
zenbaki horren balio maximoa (r1+r2) da.
Handiagoa ezin da, diskoek ez luketelako elkar joko. Talka parametroaren
balio minimoa 0 da, aurrez-aurreko talkarako.
- Diskoek hasieran ez dute abiadura angeluarrik:
ω1=ω2=0
Hasi botoia sakatu.
Ikusten da, bi diskoak nola mugitzen diren talka baino lehen eta ondoren,
laborategiko erreferentzia-sistemaren ikuspegitik.
Programak kalkulu guztiak burutzen ditu:
- Bi diskoen abiadurak talkaren ondoren: v1 eta v2.
- Bi diskoen norabideak talkaren ondoren, φ1
eta φ2
lehen diskoaren eraso-norabidearekiko.
- Bi diskoen errotazioko abiadura angeluarrak talkaren ondoren:
w1 eta
w2.
- Talkan galdutako energia: Q.
Hasieran aukeratutako datuetatik (m1, r1
eta b) eta programak kalkulatzen dituen magnitude guztietatik,
egiazta daiteke kontserbatzen direla, momentu lineal totala eta diskoen
momentu angeluar indibidualak P puntuarekiko. Gainera, diskoen momentu
angeluar totala ere kontserbatzen da.
|