Meniscos

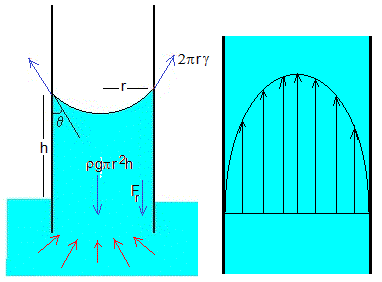
En las proximidades de la pared de un recipiente, una molécula del líquido (señalada en color rojo) experimenta las siguientes fuerzas:

• Su peso, P
• La fuerza de cohesión que ejercen el resto de las moléculas del líquido sobre dicha molécula F_c.
• La fuerza de adherencia que ejercen las moléculas de la pared sobre la molécula del líquido F_a.

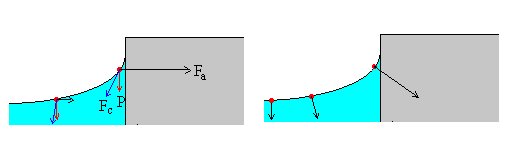
Supondremos despreciable la fuerza que ejercen sobre la molécula considerada, las moléculas de vapor por encima de la superficie del líquido.

En la figura de la izquierda, se muestran las fuerzas sobre dos moléculas, una que está muy cerca de la pared y otra que está más alejada.

En la figura de la derecha, se muestra la resultante de dichas fuerzas. La superficie es siempre normal a la resultante. Cuando las moléculas están alejadas de la pared, la resultante debida al peso y a las fuerzas de cohesión (las fuerzas de adherencia son despreciables) es vertical hacia abajo, la superficie es entonces, horizontal.

Pueden ocurrir dos casos según sea la intensidad de las fuerzas de cohesión y adherencia.

• Que el líquido moje, por ejemplo, agua en un recipiente de vidrio. Las fuerzas de adherencia son mucho mayores que las de cohesión.

En los líquidos que mojan, la resultante de las fuerzas que actúan sobre las moléculas próximas a la pared, está dirigida hacia el interior de la pared (véase la figura de la derecha), por lo que la forma de la superficie del líquido es cóncava. (menisco cóncavo).

• Que el líquido no moje, por ejemplo, mercurio en un recipiente de vidrio. Las fuerzas de cohesión son mayores que las de adherencia.

En los líquidos que no mojan, la resultante de las fuerzas que actúan sobre las moléculas próximas a la pared, está dirigida hacia el interior del líquido, por lo que la forma del la superficie del líquido será convexa (menisco convexo).

Recibe el nombre de ángulo θ de contacto, al formado por la tangente a la superficie del menisco en el punto de contacto con la pared. Este ángulo es agudo cuando el líquido moja y es obtuso cuando el líquido no moja.

Fenómenos capilares. Ley de Jurín

Si se coloca un capilar verticalmente en un recipiente de líquido que moje, el líquido asciende por el capilar, hasta alcanzar determinada altura. Si el líquido no moja, el nivel de líquido en el capilar es menor que en el recipiente.

Debido a la curvatura de una superficie se produce una sobrepresión en su interior, que ya hemos estudiado en anteriores páginas.

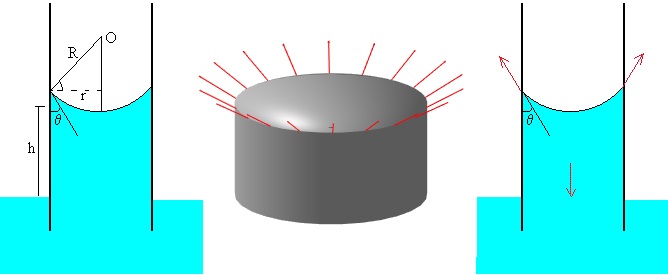
La superficie del menisco en el capilar se puede considerar como un casquete esférico de radio R. La relación entre el radio del capilar r, el radio del menisco R y el ángulo de contacto θ, es.

r=Rcosθ

Debido a la curvatura de la superficie habrá una sobrepresión hacia el centro del menisco, que de acuerdo con la ley de Laplace (superficie de una cara), valdrá

${\displaystyle \Delta p=\frac{2\gamma }{R}=\frac{2\gamma }{r}\cos \theta }$

Por efecto de esta sobrepresión, el líquido asciende una altura h.

Δp=ρgh

La altura h a la que asciende el nivel del líquido en el capilar será

${\displaystyle h=\frac{2\gamma }{rg\rho }\cos \theta }$

Esta expresión es la denominada ley de Jurín:

Otra forma de obtener esta relación, el peso de la columna de líquido se compensa con la componente vertical de la fuerza que ejerce la tensión superficial

${\displaystyle \begin{array}{l}\left(2\pi r\gamma \right)\cos \theta =\rho \left(\pi r^{2}h\right)g\\ h=\frac{2\gamma \cos \theta }{\rho rg}\end{array}}$

La altura a la que se eleva o desciende un líquido en un capilar es directamente proporcional a su tensión superficial y está en razón inversa a la densidad del líquido y del radio del tubo.

El líquido asciende por un tubo capilar

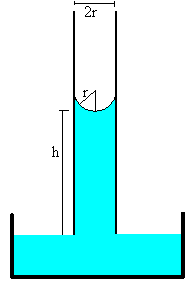
En el apartado anterior, se ha descrito el fenómeno de la elevación h de un líquido en un capilar de radio r conocido, a partir de la cual, se puede obtener la tensión superficial γ del líquido.

En este apartado, se describe el aspecto dinámico de dicha situación física. Introducimos el tubo capilar en posición vertical en un depósito grande de líquido y observaremos como se incrementa la altura de líquido en el capilar a medida que transcurre el tiempo.

Cuando el líquido de viscosidad η, asciende por el tubo capilar de radio r supondremos que fluye en régimen laminar, aplicamos la ley de Poiseuille,

${\displaystyle G=\frac{\pi }{8}\frac{\Delta p·r^4}{\eta ·h}}$

donde G es el gasto o volumen de líquido que fluye en la unidad de tiempo,

${\displaystyle G=\pi r^2\frac{dh}{dt}}$

dh/dt es el incremento de altura de líquido en el capilar en la unidad de tiempo y h es la altura de la columna de fluido en el tubo capilar en el instante t.

Δp es la diferencia de presión que hace que el líquido ascienda.

${\displaystyle \Delta p=\frac{2\gamma }{r}-\rho gh}$

Cuando esta diferencia de presión se hace cero, Δp=0, se alcanza la situación de equilibrio estudiada en el apartado anterior. El líquido deja de ascender por el tubo capilar. La altura máxima a la que asciende es

${\displaystyle h_{máx}=\frac{2\gamma }{\rho gr}}$

La ecuación diferencial que describe la variación de la altura h de líquido en el tubo capilar en función del tiempo t es,

${\displaystyle \pi r^2\frac{dh}{dt}=\frac{\pi r^4}{8\eta h}\left(\frac{2\gamma }{r}-\rho gh\right)}$

o bien,

${\displaystyle \frac{dh}{dt}=\frac{a-bh}{h}a=\frac{\gamma r}{4\eta }b=\frac{\rho g{r}^2}{8\eta }}$

Integramos la ecuación

${\displaystyle {\displaystyle \underset{0}{\overset{h}{\int }}\frac{hdh}{a-bh}}={\displaystyle \underset{0}{\overset{t}{\int }}dt}}$

Después de hacer algunas operaciones obtenemos la ecuación

${\displaystyle h+\frac{a}{b}\ln \frac{a-bh}{a}=-bt}$

Esta función implícita t=f(h) se puede hacer explícita h=g(t) expresándola en términos de la función W de Lambert

${\displaystyle \begin{array}{l}\ln \left(1-\frac{b}{a}h\right)=-\frac{b}{a}(h+bt)\hfill \\ \exp \left(-\frac{b}{a}h-\frac{b^2}{a}t\right)=-\frac{b}{a}h+1\hfill \end{array}}$

Comparamos la ecuación, a^b·x+c=d·x+f con su expresión en términos de la función W de Lambert

${\displaystyle x=\frac{-1}{b\ln a}W\left(\frac{-b}{d}\left(\ln a\right)a^{c-bf/d}\right)-\frac{f}{d}}$

Sustituyendo la variable x por h, obtenemos

${\displaystyle \begin{array}{l}h=-\frac{1}{-\frac{b}{a}\ln e}W\left(-\frac{-\frac{b}{a}}{-\frac{b}{a}}(\ln e)\exp \left(-\frac{b^2}{a}t-\frac{-\frac{b}{a}·1}{-\frac{b}{a}}\right)\right)-\frac{1}{-\frac{b}{a}}\\ h=\frac{a}{b}W\left(-\exp \left(-\frac{b^2}{a}t-1\right)\right)+\frac{a}{b}\end{array}}$

%agua
tensionSup=0.0728; %tensión superficial del agua
densidad=1000; %densidad
viscosidad=0.00105; %viscosidad
radio=0.1/1000; %radio capilar en m
a=tensionSup*radio/(4*viscosidad);
b=densidad*9.8*radio^2/(8*viscosidad);

f=@(t) a*lambertw(0,-exp(-1-b^2*t/a))/b+a/b;
fplot(f,[0,250])
grid on
xlabel('t(s)')
ylabel('h(m)')
title('Fenómeno capilar')

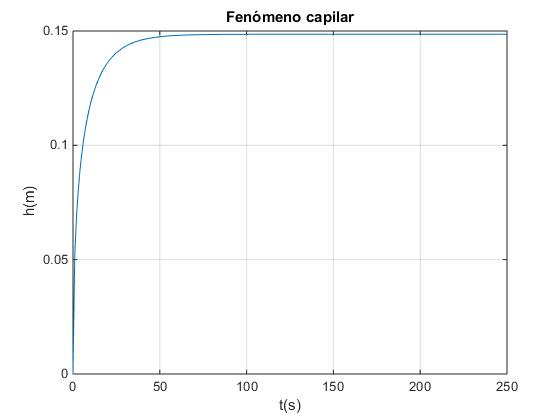
Cuando t tiende a infinito h tiende al cociente a/b.

${\displaystyle h_{máx}=\frac{a}{b}=\frac{2\gamma }{\rho gr}}$

>>  hMax=2*tensionSup/(densidad*9.8*radio)
hMax =    0.1486

La altura máxima h_max es independiente de la viscosidad del fluido η, pero el tiempo que tarda en alcanzar aproximadamente esta altura, depende de la viscosidad, una situación análoga a la carga de un condensador a través de una resistencia, o a la velocidad que alcanza una esfera que se deja caer en el seno de un fluido viscoso.

La ecuación que nos da h en función del tiempo t, no es idéntica, a la ecuación que nos da la carga del condensador en función del tiempo.

Actividades:

• Se elige el líquido, en el control titulado Líquidos

• Se elige el radio del capilar (en mm) en el control titulado Radio capilar.

Se pulsa el botón titulado Nuevo.

El tubo capilar en posición vertical se pone en contacto con el líquido y se observa como asciende el líquido en el tubo capilar.

Los datos de los líquidos examinados se indican en el siguiente cuadro, expresados en el S.I. de unidades.

Fuente: Manual de Física Elemental. Koshkin N. I., Shirkévich M. G. Edtorial Mir (1975)

El aceite y la glicerina tienen viscosidades η elevadas, por lo que estos líquidos ascienden lentamente en el tubo capilar en comparación con el agua y en el alcohol. El radio r del capilar juega también un papel importante. Aunque un radio mayor disminuye la diferencia de presión Δp, aumenta sin embargo, la rapidez con la que asciende el líquido

Una descripción más completa

Cómo asciende un líquido en un tubo capilar es un fenómeno complejo para el cual existen varias explicaciones, la más sencilla es la descrita en el apartado anterior. Se trata de un problema de masa variable bajo la acción de las fuerzas debidas a la tensión superficial, al peso y a las fuerzas de rozamiento (viscoso) y otras fuerzas.

Se supondrá que el flujo de líquido a través del tubo capilar tiene un perfil de velocidades parabólico como indica la ley de Poiseuille

Se inserta un tubo capilar vertical en un depósito de líquido muy grande. En el instante t=0, h=0, y dh/dt=0. Debido a la componente vertical de la fuerza que ejerce la tensión superficial, el líquido se acelera dentro del tubo capilar. Mientras el fluido asciende, el rozamiento con el tubo y el peso del líquido se oponen y la columna de líquido empieza a decelerarse hasta que finalmente se detiene cuando alcanza la altura máxima h_∞ dada por la ley de Jurín para t→∞

${\displaystyle h_{\infty }=\frac{2\gamma }{rg\rho }\cos \theta }$

Pueden ocurrir dos casos, que la altura de fluido h(t) tienda hacia el valor asintótico h_∞

• oscilando
• sin oscilar

La ecuación diferencial que describe estos dos comportamientos es

${\displaystyle \left(h+\frac{37}{36}r\right)\frac{d^{2}h}{d{t}^2}+\frac{7}{6}{\left(\frac{dh}{dt}\right)}^2+\frac{\eta }{\rho }\left(\frac{8h}{r^2}+\frac{2}{r}\right)\frac{dh}{dt}+gh=\frac{2\gamma }{\rho r}\cos \theta }$

En el estado estacionario, se alcanza la altura h_∞

Resolvemos esta ecuación diferencial por procedimientos numéricos con los siguientes datos

• Viscosidad, η=2.2·10^-4 kg/(m·s)
• Coeficiente de tensión superficial, γ=1.67·10^-2 N/m
• Angulo de contacto, θ=26°
• Densidad, ρ=710 kg/m³

Para cinco radios del tubo capilar: r=0.1 0.2, 0.3, 0.4 y 0.5 mm

eta=2.2e-4; %viscosidad
gamma=1.67e-2; %tensión superficial
th=26*pi/180; %ángulo de contacto
rho=710; %densidad
hold on
for k=1:5
    r=0.0001*k; %radio del tubo capilar
    f=@(t,x) [x(2);(2*gamma*cos(th)/(rho*r)-7*x(2)^2/6-
eta*(8*x(1)/r^2+2/r)*x(2)/rho-9.81*x(1))/(x(1)+37*r/36)]; 
    [t,x]=ode45(f,[0,1],[0,0]);
    plot(t,x(:,1))
end
hold off
grid on
legend('i=1','i=2','i=3','i=4','i=5','Location','best')
xlabel('t')
ylabel('h');
title('Capilar')

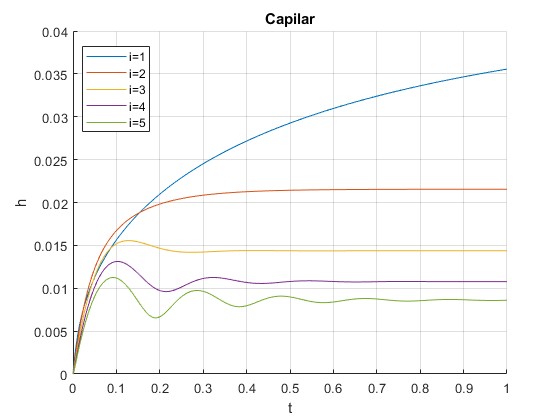
Observamos los dos tipos de comportamiento, oscilando alrededor de h_∞ para r=0.5, 0.4 y 0.3 mm, sin oscilar r=0.2 y 0.1 mm

Una solución analítica que no contempla las oscilaciones alrededor de la altura final h_∞ es

${\displaystyle \begin{array}{l}h(t)=\frac{2\gamma \cos \theta }{\rho gr}\left\{1-\left(1+t\sqrt{\frac{6g}{7r}}+\alpha t^3\right)\exp \left(-t\sqrt{\frac{6g}{7r}}\right)\right\}\\ \alpha \approx \frac{7\eta \gamma \cos \theta }{12{\rho }^2{r}^5}-\frac{1}{15}{\left(\sqrt{\frac{6g}{7r}}\right)}^3\end{array}}$

En el estado estacionario, t→∞, h(t)→h_∞

La velocidad y la aceleración son, respectivamente,

${\displaystyle \begin{array}{l}\frac{dh}{dt}=\frac{2\gamma \cos \theta }{\rho gr}\left(\frac{6g}{7r}-3\alpha t+t^2\alpha \sqrt{\frac{6g}{7r}}\right)t\exp \left(-t\sqrt{\frac{6g}{7r}}\right)\\ \frac{d^{2}h}{d{t}^2}=\frac{2\gamma \cos \theta }{\rho gr}\left\{\frac{6g}{7r}-\left(6\alpha +{\left(\frac{6g}{7r}\right)}^{3/2}\right)t+6\alpha \sqrt{\frac{6g}{7r}}{t}^2-\alpha \frac{6g}{7r}{t}^3\right\}\exp \left(-t\sqrt{\frac{6g}{7r}}\right)\end{array}}$

Representamos la altura h(t), la velocidad dh/dt y la aceleración d²h/dt², con los datos siguienets

• Viscosidad, η=2.2·10^-4 kg/(m·s)
• Coeficiente de tensión superficial, γ=1.67·10^-2 N/m
• Angulo de contacto, θ=26°
• Densidad, ρ=710 kg/m³
• Radio del tubo capilar, r= 0.5 mm

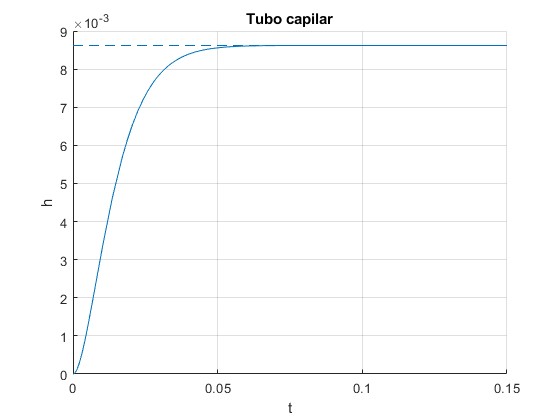
1. Altura, h(t)

eta=2.2e-4; %viscosidad
gamma=1.67e-2; %tensión superficial
th=26*pi/180; %ángulo de contacto
rho=710; %densidad
r=0.0005; %radio del tubo capilar
alfa=7*eta*gamma*cos(th)/(12*rho^2*r^5)-sqrt(6*9.81/(7*r))^3/15;
h=@(t) 2*gamma*cos(th)*(1-(1+t*sqrt(6*9.81/(7*r))+alfa*t.^3).
*exp(-t*sqrt(6*9.81/(7*r))))/(rho*9.81*r);
H=2*gamma*cos(th)/(rho*9.81*r);
hold on
line([0,0.15],[H,H],'lineStyle','--')
fplot(h,[0,0.15])
hold off
grid on
ylim([0,0.009])
xlabel('t')
ylabel('h')
title('Tubo capilar')



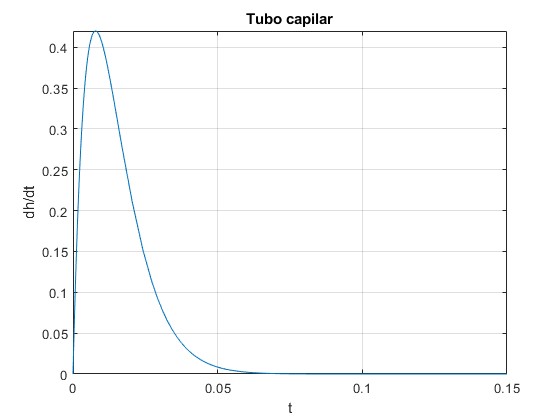
2. Velocidad, dh/dt

eta=2.2e-4; %viscosidad
gamma=1.67e-2; %tensión superficial
th=26*pi/180; %ángulo de contacto
rho=710; %densidad
r=0.0005; %radio del tubo capilar
alfa=7*eta*gamma*cos(th)/(12*rho^2*r^5)-sqrt(6*9.81/(7*r))^3/15;
h=@(t) 2*gamma*cos(th)*(1-(1+t*sqrt(6*9.81/(7*r))+alfa*t.^3).*
exp(-t*sqrt(6*9.81/(7*r))))/(rho*9.81*r);
H=2*gamma*cos(th)/(rho*9.81*r);
hold on
line([0,0.15],[H,H],'lineStyle','--')
fplot(h,[0,0.15])
hold off
grid on
ylim([0,0.009])
xlabel('t')
ylabel('h')
title('Tubo capilar')



3. Aceleración, d²h/dt²

eta=2.2e-4; %viscosidad
gamma=1.67e-2; %tensión superficial
th=26*pi/180; %ángulo de contacto
rho=710; %densidad
r=0.0005; %radio del tubo capilar
alfa=7*eta*gamma*cos(th)/(12*rho^2*r^5)-sqrt(6*9.81/(7*r))^3/15;
v=@(t) 2*gamma*cos(th)*(6*9.81/(7*r)-(6*alfa+(6*9.81/(7*r))^(3/2))*t+
6*alfa*sqrt(6*9.81/(7*r))*t.^2-6*9.81*alfa*t.^3/(7*r)).
*exp(-t*sqrt(6*9.81/(7*r)))/(rho*9.81*r);
fplot(v,[0,0.15])
grid on
ylim([-25,150])
xlabel('t')
ylabel('d^2h/dt^2')
title('Tubo capilar')



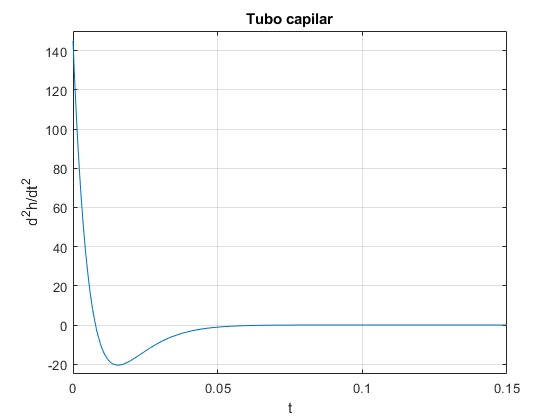
La aceleración producida por la componente vertical de la fuerza que origina la tensión superficial, va disminuyendo con el incremento del peso de la columna de fluido y la fuerza de rozamiento

Referencias

Peiris M. G. C. , Tenmakone K.. Rate of rise of a liquid in a capillary tube. Am. J. Phys. 48 (5) May 1980, pp. 415

BoHua Sun. The monotonic rising and oscillating of capillary driven flow in circular cylindrical tubes. AIP Advances. February 2021

BoHua Sun. Singularity-free approximate analytical solution of capillary rise dynamics. SCIENCE CHINA Physics, Mechanics &! Astronomy. August 2018, Vol. 61, No. 8: 084721