Consideremos una membrana circular de radio a, que está fija por su borde. La ecuación del movimiento ondulatorio en coordenadas polares se escribe.

${\displaystyle \frac{{\partial }^2\Psi }{\partial t^2}=c^2\left(\frac{{\partial }^2\Psi }{\partial {\rho }^2}+\frac{1}{\rho }\frac{\partial \Psi }{\partial \rho }+\frac{1}{{\rho }^2}\frac{{\partial }^2\Psi }{\partial {\phi }^2}\right)}$

Simetría radial

Estudiamos primero, el caso más sencillo, las soluciones Ψ(r,t)independientes del ángulo φ.

${\displaystyle \frac{{\partial }^2\Psi }{\partial t^2}=c^2\left(\frac{{\partial }^2\Psi }{\partial {\rho }^2}+\frac{1}{\rho }\frac{\partial \Psi }{\partial \rho }\right)}$

Condiciones iniciales y de contorno

Las condiciones de contorno son

${\displaystyle \Psi (a\mathrm{,0})=0t\ge 0}$

Las condiciones iniciales son:

${\displaystyle t=0\{\begin{array}{l}\Psi (\rho \mathrm{,0})={\Psi }_0(\rho )\\ {\frac{\partial \Psi (\rho ,t)}{\partial t}|}_{t=0}={\dot{\Psi }}_0(\rho )\end{array}}$

Modos de vibración

Aplicamos el procedimiento de separación de variables

${\displaystyle \Psi (\rho ,t)=R(\rho )·T(t)}$

Sustituimos en la ecuación diferencial

${\displaystyle \frac{1}{T(t)}·\frac{d^{2}T}{d{t}^2}=\frac{c^2}{R(\rho )}\left(\frac{d^{2}R}{d{\rho }^2}+\frac{1}{\rho }\frac{dR}{d\rho }\right)}$

Como el miembro izquierdo depende solamente de t y el derecho solamente de ρ, entonces, igualamos ambos a una constante que denominaremos -ω².

${\displaystyle \begin{array}{l}\frac{1}{T(t)}·\frac{d^{2}T}{d{t}^2}=\frac{c^2}{R(\rho )}\left(\frac{d^{2}R}{d{\rho }^2}+\frac{1}{\rho }\frac{dR}{d\rho }\right)=-{\omega }^2\\ \{\begin{array}{l}\frac{d^{2}R}{d{\rho }^2}+\frac{1}{\rho }\frac{dR}{d\rho }+{\frac{\omega }{c^2}}^{2}R=0\\ \frac{d^{2}T}{d{t}^2}+{\omega }^{2}T(t)=0\end{array}\end{array}}$

Definimos una nueva variable x=ω·ρ/c.

${\displaystyle \begin{array}{l}\frac{d^{2}R}{d{x}^2}+\frac{1}{x}\frac{dR}{dx}+R=0\\ x^2\frac{d^{2}R}{d{x}^2}+x\frac{dR}{dx}+x^{2}R=0\end{array}}$

Esta es la ecuación de Bessel de orden cero. La solución de esta ecuación es

${\displaystyle R=C·J_0(x)+D·Y_0(x)}$

Como Y₀(x) se hace infinito cuando s se aproxima a cero, el coeficiente D deberá ser cero.

${\displaystyle R(\rho )=J_0\left(\frac{\omega }{c}\rho \right)}$

La condición de contorno implica que para todo t, Ψ(a,t)=0 por lo que R(a)=0. Las raíces de la ecuación

J₀(α)=0 con α=ω·a/c.

son α₁=2.405, α₂=5.520, α₃=8.654,.... Los sucesivos valores de α determinan las frecuencias ω₁, ω₂ .... ω_n, de los distintos modos de vibración.

Representamos gráficamente J₀(x)

>> x=linspace(0,20,200);
>> plot(x,besselj(0,x),'b')
>> xlabel('x')
>> ylabel('y')
>> title('Raíces de J_0')
>> grid on

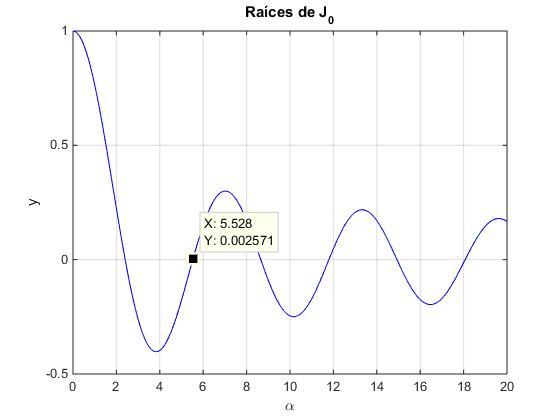
Con la herramienta Data cursor, determinamos los valores aproximados de las raíces: 2.4, 5.5, 8.6, 11.8, 14.9...

La función raices calcula las raíces múltiples de la función f(x) buscando los intervalos en los que dicha función cambia de signo y utilizando la función MATLAB fzero para encontrarlas

function r = raices(f, x)
    y=f(x);
    indices=find(y(1:end-1).*y(2:end)<0);
    r=zeros(1,length(indices));
    for k=1:length(indices)
        r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
    end
end

>> x=linspace(0,20,20);
>> raices(@(x) besselj(0,x),x)
ans =    2.4048    5.5201    8.6537   11.7915   14.9309   18.0711

La diferencia entre dos raíces consecutivas se aproxima a π.

Representamos el tercer modo de vibración

%raíces
x=linspace(0,20,20);
f=@(x) besselj(0,x);
alfa=raices(f,x);

a=1; %radio de la membrana circular
r=0:0.01:1;
ang=0:pi/50:2*pi;
[r,ang]=meshgrid(r,ang);
x=r.*cos(ang);
y=r.*sin(ang);
z=besselj(0,alfa(3)*r/a); %tercer modo
surf(x,y,z)
xlabel('x')
ylabel('y')
zlabel('z')
title('Vibración de una membrana circular')

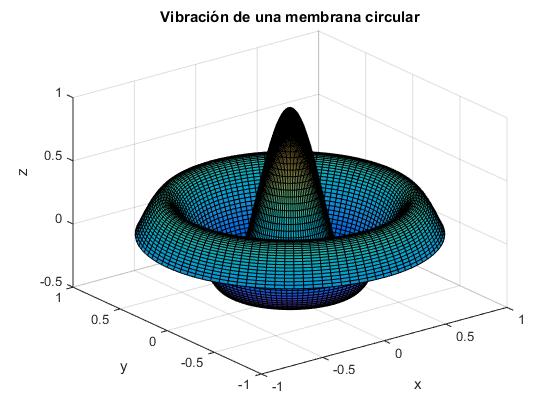
La solución de la ecuación diferencial dependiente del tiempo es tambien conocida

${\displaystyle \begin{array}{l}\frac{d^{2}T}{d{t}^2}+{\omega }^2·T=0\\ T_n(t)=A_n\cos ({\omega }_{n}t)+B_n\sin ({\omega }_{n}t)\end{array}}$

La solución de la ecuación diferencial correspondiente al modo n de vibración de la membrana circular es

${\displaystyle {\Psi }_n(\rho ,t)=R_n(\rho )T_n(t)=J_0\left(\frac{{\alpha }_n}{a}\rho \right)\left(A_n\cos ({\omega }_{n}t)+B_n\sin ({\omega }_{n}t)\right)}$

Solución completa

La solución general que satisface las condiciones de contorno es la superposición

${\displaystyle \Psi (\rho ,t)={\displaystyle \sum _{n=1}^{\infty }{\Psi }_n(\rho ,t)}={\displaystyle \sum _{n=1}^{\infty }{J}_0\left(\frac{{\alpha }_n}{a}\rho \right)\left(A_n\cos ({\omega }_{n}t)+B_n\sin ({\omega }_{n}t)\right)}}$

Esta ecuación describe todos los posibles modos de vibración de la membrana circular. La vibración particular que experimenta la membrana está únicamente determinada por las condiciones iniciales, que a su vez determinan los valores de las constantes A_n y B_n.

${\displaystyle \Psi (\rho ,0)={\displaystyle \sum _{n=1}^{\infty }{J}_0\left(\frac{{\alpha }_n}{a}\rho \right)A_n}}$

Utilizamos las propiedades de las funciones de Bessel para calcular el coeficiente A_n

${\displaystyle \begin{array}{l}\underset{0}{\overset{a}{{\displaystyle \int }}}\rho \Psi (\rho ,0)J_0\left(\frac{{\alpha }_n}{a}\rho \right)d\rho ={\displaystyle \sum _{n=1}^{\infty }{A}_n{\displaystyle \underset{0}{\overset{a}{\int }}\rho J_0\left(\frac{{\alpha }_n}{a}\rho \right)J_0\left(\frac{{\alpha }_m}{a}\rho \right)d\rho }}\\ \underset{0}{\overset{a}{{\displaystyle \int }}}\rho \Psi (\rho ,0)J_0\left(\frac{{\alpha }_n}{a}\rho \right)d\rho =a^2{\displaystyle \sum _{n=1}^{\infty }{A}_n{\displaystyle \underset{0}{\overset{1}{\int }}u{J}_0\left({\alpha }_{n}u\right)J_0\left({\alpha }_{m}u\right)du}}\\ A_n=\frac{2}{a^2{J}_1^2({\alpha }_n)}\underset{0}{\overset{a}{{\displaystyle \int }}}\rho \Psi (\rho ,0)J_0\left(\frac{{\alpha }_n}{a}\rho \right)d\rho n=\mathrm{1,2,3...}\end{array}}$

Téngase en cuenta que α_n son las raíces de la ecuación J₀(x)=0

Del mismo modo, procedemos para calcular los coeficientes B_n

${\displaystyle \begin{array}{l}{\frac{\partial \Psi (\rho ,t)}{\partial t}|}_{t=0}={\displaystyle \sum _{n=1}^{\infty }{J}_0\left(\frac{{\alpha }_n}{a}\rho \right){\omega }_n{B}_n}\\ B_n=\frac{2}{a^2{J}_1^2({\alpha }_n){\omega }_n}\underset{0}{\overset{a}{{\displaystyle \int }}}\rho \left({\frac{\partial \Psi (\rho ,t)}{\partial t}|}_{t=0}\right)J_0\left(\frac{{\alpha }_n}{a}\rho \right)d\rho n=\mathrm{1,2,3...}\end{array}}$

Condiciones iniciales, t=0

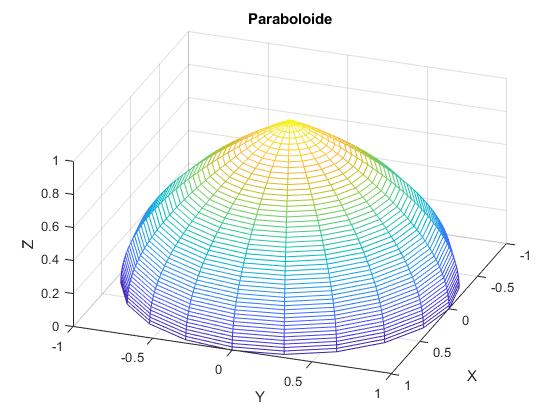
Consideremos una membrana de radio a, que en el instante inicial t=0, tiene la forma de paraboloide de revolución

${\displaystyle \Psi (\rho ,0)=A\left(1-\frac{{\rho }^2}{a^2}\right)}$

Representamos la superficie de revolución dada por la función z=1-x²/a²

a=1; %radio de la membrana
x=linspace(0, a, 50);
z=1-x.^2/a^2; 
[X,Y,Z]=cylinder(z);
mesh(X,Y,Z);
xlabel('X'); ylabel('Y'); zlabel('Z') 
title('Paraboloide')
view(110,40)

Como la membrana está en reposo en el instante t=0, los coeficientes B_n=0. Calculamos los coeficientes A_n

${\displaystyle A_n=\frac{2}{a^2{J}_1^2({\alpha }_n)}{\displaystyle \underset{0}{\overset{a}{\int }}\rho A\left(1-\frac{{\rho }^2}{a^2}\right)J_0\left(\frac{{\alpha }_n}{a}\rho \right)d\rho }n=\mathrm{1,2,3...}}$

Teniendo en cuenta el resultado de las integrales

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{a}{\int }}x}{J}_0(x)·dx=a{J}_1(a)\\ {\displaystyle \underset{0}{\overset{a}{\int }}{x}^3}{J}_0(x)·dx=2a^2{J}_0(a)+\left(a^3-4a\right)J_1(a)\end{array}}$

>> syms x a;
>> int(besselj(0,x)*x,x,0,a)
ans =a*besselj(1, a)
>> int(besselj(0,x)*x^3,x,0,a)
ans =2*a^2*besselj(0, a) - 4*a*besselj(1, a) + a^3*besselj(1, a)

Llegamos al siguiente resultado

${\displaystyle \begin{array}{l}{A}_n=\frac{2A}{a^2{J}_1^2({\alpha }_n)}\left\{{\displaystyle \underset{0}{\overset{a}{\int }}\rho J_0\left(\frac{{\alpha }_n}{a}\rho \right)d\rho }-\frac{1}{a^2}{\displaystyle \underset{0}{\overset{a}{\int }}{\rho }^3{J}_0\left(\frac{{\alpha }_n}{a}\rho \right)d\rho }\right\}=\\ \frac{2A}{a^2{J}_1^2({\alpha }_n)}\left\{\frac{a^2}{{\alpha }_n^2}{x{J}_1(x)|}_0^{{\alpha }_n}-\frac{1}{a^2}\frac{a^4}{{\alpha }_n^4}{\left(2x^2{J}_0(x)+\left(x^3-4x\right)J_1(x)\right)|}_0^{{\alpha }_n}\right\}=\\ \frac{2A}{a^2{J}_1^2({\alpha }_n)}\left\{\frac{a^2}{{\alpha }_n}{J}_1({\alpha }_n)-\frac{a^2}{{\alpha }_n^4}\left(2{\alpha }_n^2{J}_0({\alpha }_n)+\left({\alpha }_n^3-4{\alpha }_n\right)J_1({\alpha }_n)\right)\right\}=\frac{8A}{{\alpha }_n^3{J}_1({\alpha }_n)}\end{array}}$

Téngase en cuenta que α_n son las raíces de la ecuación J₀(x)=0

La solución de la ecuación diferencial del movimiento ondulatorio con las condiciones de contorno especificadas (bordes fijos) y la froma inicial de la membrana en reposo es

${\displaystyle \Psi (\rho ,t)=8A{\displaystyle \sum _{n=1}^{\infty }\frac{J_0\left(\frac{{\alpha }_n}{a}\rho \right)}{{\alpha }_n^3{J}_1({\alpha }_n)}\cos \left(\frac{c{\alpha }_n}{a}t\right)}}$

Comprobamos que la forma inicial de la membrana se obtiene para t=0. Tomaremos varias raíces de la ecuación J₀(α)=0

function membrana_4
    a=1; %radio de la membrana
    c=1; %velocidad de propagación
    t=0; %instante inicial
    %raíces
    x=linspace(0,20,20);
    f=@(x) besselj(0,x);
    alfa=raices(f,x);

    x=linspace(0, a, 50);
    z=onda(x);
    [X,Y,Z]=cylinder(z);
    mesh(X,Y,Z);
    xlabel('X'); ylabel('Y'); zlabel('Z') 
    title('Paraboloide')
    view(110,40)

    function z=onda(x)
        z=0;   
        for n=1:length(alfa)
            z=z+besselj(0,alfa(n)*x/a)*cos(c*alfa(n)*t/a)/
(alfa(n)^3*+besselj(1,alfa(n)));
        end
        z=z*8;
    end

    function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for k=1:length(indices)
            r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
        end
    end
end

Modos de vibración de una membrana circular (solución general)

Consideremos una membrana circular de radio a, que está fija por su borde. La ecuación del movimiento ondulatorio se escribe.

${\displaystyle \frac{{\partial }^2\Psi }{\partial t^2}=c^2\left(\frac{{\partial }^2\Psi }{\partial {\rho }^2}+\frac{1}{\rho }\frac{\partial \Psi }{\partial \rho }+\frac{1}{{\rho }^2}\frac{{\partial }^2\Psi }{\partial {\phi }^2}\right)}$

Aplicamos el método de separación de variables y sustituimos en la ecuación diferencial

${\displaystyle \begin{array}{l}\Psi (\rho ,t)=F(\rho ,\phi )·T(t)\\ \frac{1}{T(t)}·\frac{d^{2}T}{d{t}^2}=\frac{c^2}{F(\rho ,\phi )}\left(\frac{{\partial }^{2}F}{\partial {\rho }^2}+\frac{1}{\rho }\frac{\partial F}{\partial \rho }+\frac{1}{{\rho }^2}\frac{{\partial }^{2}F}{\partial {\phi }^2}\right)=-{\omega }^2\end{array}}$

Como el miembro izquierdo depende solamente de t y el derecho solamente de r y φ, entonces, igualamos ambos a una constante que denominaremos -ω².

${\displaystyle \{\begin{array}{l}\frac{{\partial }^{2}F}{\partial {\rho }^2}+\frac{1}{\rho }\frac{\partial F}{\partial \rho }+\frac{1}{{\rho }^2}\frac{{\partial }^{2}F}{\partial {\phi }^2}+\frac{{\omega }^2}{c^2}F=0\\ \frac{d^{2}T}{d{t}^2}+{\omega }^{2}T(t)=0\end{array}}$

Aplicamos el método de separación de variables a la primera ecuación diferencial

${\displaystyle \begin{array}{l}F(\rho ,\phi )=R(\rho )·\Phi (\phi )\\ \Phi (\phi )\left({\rho }^2\frac{d^{2}R}{d{\rho }^2}+\rho \frac{dR}{d\rho }\right)+R(\rho )\frac{d^2\Phi }{d{\phi }^2}+\frac{{\omega }^2}{c^2}{\rho }^{2}R(\rho )\Phi (\phi )=0\\ -\frac{1}{R(\rho )}\left({\rho }^2\frac{d^{2}R}{d{\rho }^2}+\rho \frac{dR}{d\rho }+\frac{{\omega }^2}{c^2}{\rho }^{2}R(\rho )\right)=\frac{1}{\Phi (\phi )}\frac{d^2\Phi }{d{\phi }^2}=-m^2\end{array}}$

Obteniendo el sistema de ecuaciones diferenciales

${\displaystyle \{\begin{array}{l}\frac{d^{2}R}{d{\rho }^2}+\frac{1}{\rho }\frac{dR}{d\rho }+\left(\frac{{\omega }^2}{c^2}-\frac{m^2}{{\rho }^2}\right)R=0\\ \frac{d^2\Phi }{d{\phi }^2}+m^2\Phi =0\end{array}}$

Multiplicamos la primera por ρ² y hacemos el cambio de variable x=ρω/c. Obtenemos la ecuación de Bessel

${\displaystyle \begin{array}{l}{x}^2\frac{d^{2}y}{d{x}^2}+x\frac{dy}{dx}+(x^2-m^2)y=0\\ y=A{J}_m(x)+B{Y}_m(x)\end{array}}$

La solución del sistema de dos ecuaciones diferenciales es

${\displaystyle \{\begin{array}{l}R(\rho )=C_{\rho }{J}_m\left(\frac{\omega }{c}\rho \right)+D_{\rho }{Y}_m\left(\frac{\omega }{c}\rho \right)\\ \Phi (\phi )=C_{\phi }\cos (m\phi )+D_{\phi }\sin (m\phi )\end{array}}$

Donde m es un número entero m=0,1,2,3...

Como Y(ρ) se hace infinito cuando ρ se aproxima a cero, el coeficiente D_ρ deberá ser cero, como en el caso anterior.

Representamos las primeras funciones J_m(x), para m=0,1,2,3

hold on
for m=0:3
    fplot(@(x) besselj(m,x),[0,20],'displayName',num2str(m))
end
hold off
xlabel('x')
ylabel('y')
title('J_m')
legend('-DynamicLegend','location','Best')
grid on

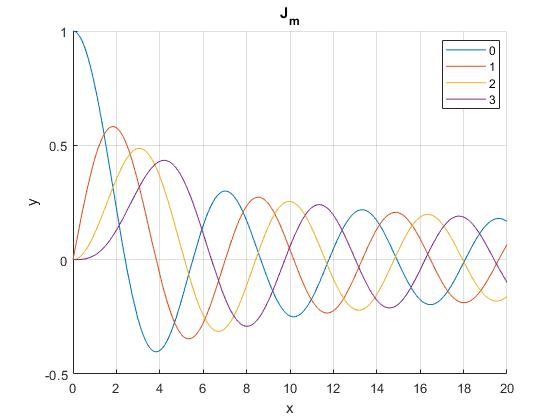
Como la función radial R(r) se hace cero cuando r=a en el borde de la membrana circular. Calculamos las raíces de 1,2,3...n de la función J_m(x) que denominaremos α_m,n, Los sucesivos valores de α=ω·R/c determinan las frecuencias ω_m1, ω_m2 .... ω_mn, de los distintos modos de vibración.

x=linspace(0,20,20);
for m=0:3;
    alfa=raices(@(x) besselj(m,x),x);
    disp([m,alfa])
end

    0         2.4048    5.5201    8.6537   11.7915   14.9309   18.0711
    1.0000    3.8317    7.0156   10.1735   13.3237   16.4706   19.6159
    2.0000    5.1356    8.4172   11.6198   14.7960   17.9598
    3.0000    6.3802    9.7610   13.0152   16.2235   19.4094

Las primeras raíces de las funciones de Bessel J_m(x) son

El modo de vibración m,n se describe por la función

${\displaystyle \begin{array}{l}{\Psi }_{m,n}(\rho ,\phi ,t)=\\ J_m\left({\alpha }_{m,n}\frac{\rho }{R}\right)·\left(C_n\cos (m\phi )+D_n\sin (m\phi )\right)·\left(A_n\cos ({\omega }_{m,n}t)+B_n\sin ({\omega }_{m,n}t)\right)\\ m=\mathrm{0,1,2,...}n=\mathrm{1,2,3...}\end{array}}$

Los primeros modos de vibración de una membrana circular. Las líneas en color rojo señalan los nodos, los puntos de la membrana que no vibran para un modo particular. Más abajo, veremos la representación en 3D de los distintos modos (m,n) de vibración

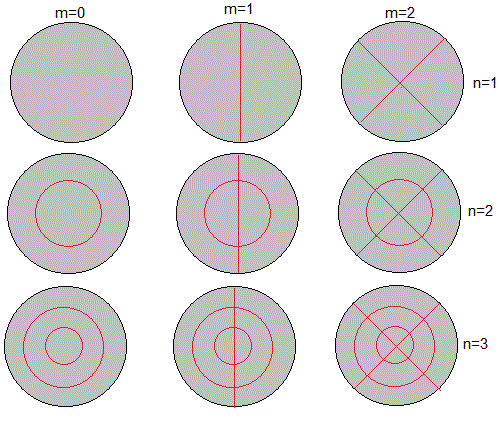
Los nodos corresponden a las raíces de la ecuación

${\displaystyle J_m\left({\alpha }_{m,n}\frac{\rho }{a}\right)=0}$

Consideremos el caso n=2. Supongamos que hemos calculado las raíces (véase la tabla más arriba) α₀₁=5.5201 (segunda raíz de J₀(x)), α₁₁=7.0156 (segunda raíz de J₁(x)), α₂₁=8.4172 (segunda raíz de J₂(x))

alfa=[5.5201,7.0156,8.4172];
for m=0:2
    f=@(x) besselj(m,alfa(m+1)*x);
    r=fzero(f, 0.5);
    disp(r)
end

Radios ρ/a de los nodos

    0.4356
    0.5462
    0.6101

Consideremos el caso n=3. Supongamos que hemos calculado las raíces (véase la tabla más arriba) α₀₂=8.6537 (tercera raíz de J₀(x)), α₁₂=10.1735 (tercera raíz de J₁(x)), α₂₂=11.6198 (tercera raíz de J₂(x))

alfa=[8.6537,10.1735,11.6198];
for m=0:2
    f=@(x) besselj(m,alfa(m+1)*x);
    r1=fzero(f, 0.2);
    r2=fzero(f, 0.8);
    disp([r1,r2])
end

Radios ρ/a de los nodos

    0.2779    0.6379
    0.3766    0.6896
    0.4420    0.7244

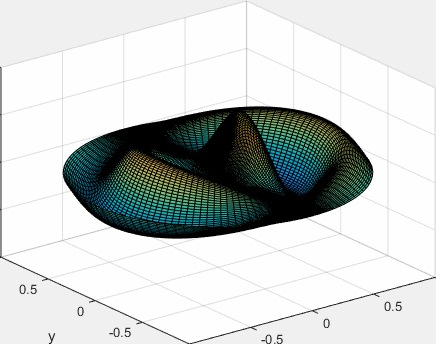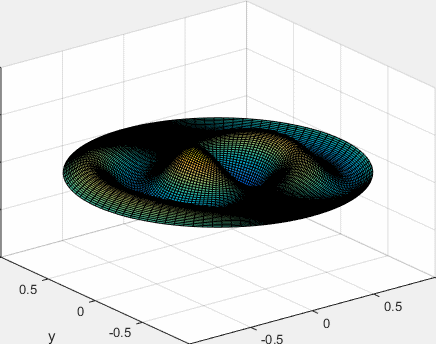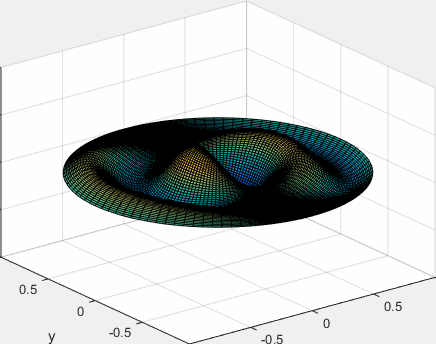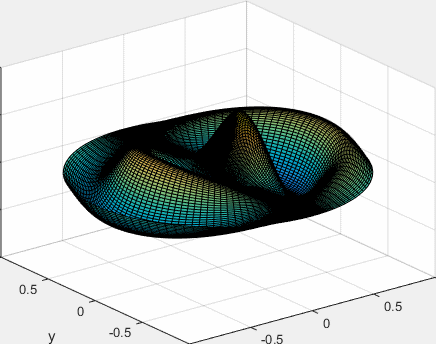
Representamos el modo de vibración de la membrana circular, para m=1 y para n=3, tercera raíz de J₁(x)

${\displaystyle {\Psi }_{m,n}(\rho ,\phi ,t)=J_m\left({\alpha }_{m,n}\frac{\rho }{a}\right)·\cos (m\phi )·\cos ({\omega }_{m,n}t)}$

La función seno se podría poner en vez de coseno.

alpha=10.1735; % raiz n=3 de J1(x) 
R=1; %radio de la membrana circular
r=0:0.01:R;
ang=0:pi/50:2*pi;
[r,ang]=meshgrid(r,ang);
x=r.*cos(ang);
y=r.*sin(ang);
fichero = 'placa_c.gif';
P=1;
m=1; %modo de vibración
n=3;
for t=0:P/20:P
    z = besselj(m,alpha*r/R).*cos(m*ang)*cos(2*pi*t/P);
    surf(x,y,z)
    xlabel('x')
    ylabel('y')
    zlabel('z')
    title('Vibración de una membrana circular')
    axis([-1 1 -1 1 -1 1]);
    
    frame=getframe;
    im = frame2im(frame);
    [imind,cm] = rgb2ind(im,256);
    if t==0
        imwrite(imind,cm,fichero,'gif','DelayTime',0,'loopcount',inf);
    else
        imwrite(imind,cm,fichero,'gif','DelayTime',0,'writemode','append');
    end
end

Modos de vibración de un anillo

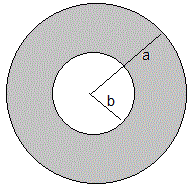
Supongamos una membrana en forma de anillo de radio exterior a y radio interior b

Partimos de la solución de las dos ecuaciones diferenciales, que hemos deducido en el apartado titulado 'Modos de vibración de una membrana circular (solución general)'

${\displaystyle \{\begin{array}{l}R(\rho )=C_{\rho }{J}_m\left(\frac{\omega }{c}\rho \right)+D_{\rho }{Y}_m\left(\frac{\omega }{c}\rho \right)\\ \Phi (\phi )=C_{\phi }\cos (m\phi )+D_{\phi }\sin (m\phi )\end{array}}$

La función R(r) se tiene que hacer cero para ρ=a y para ρ=b. Obtenemos un sistema homogéneo de dos ecuaciones con dos incógnitas C y D.

${\displaystyle \{\begin{array}{l}C{J}_m\left(\frac{\omega }{c}a\right)+D{Y}_m\left(\frac{\omega }{c}a\right)=0\\ C{J}_m\left(\frac{\omega }{c}b\right)+D{Y}_m\left(\frac{\omega }{c}b\right)=0\end{array}}$

Despejamos C en la primera ecuación y lo sustituimos en la segunda, obteniendo una ecuación trascendente en x=ω/c

${\displaystyle J_m\left(\frac{\omega }{c}a\right)Y_m\left(\frac{\omega }{c}b\right)-Y_m\left(\frac{\omega }{c}a\right)J_m\left(\frac{\omega }{c}b\right)=0}$

a=4; %radios
b=2;
x=linspace(0,10,20);
for m=0:3;
    f=@(x) bessely(m,x*b).*besselj(m,x*a)-besselj(m,x*b).*bessely(m,x*a);
    k=raices(f,x);
    disp([m,k])
end

         0    1.5615    3.1367    4.7091    6.2807    7.8520    9.4231
    1.0000    1.5983    3.1562    4.7222    6.2906    7.8599    9.4297
    2.0000    1.7035    3.2139    4.7614    6.3202    7.8837    9.4496
    3.0000    1.8644    3.3080    4.8261    6.3692    7.9231    9.4825

La solución R(ρ) es

${\displaystyle R_{mn}(\rho )=Y_m\left(\frac{{\omega }_{mn}}{c}b\right)J_m\left(\frac{{\omega }_{mn}}{c}\rho \right)-J_m\left(\frac{{\omega }_{mn}}{c}b\right)Y_m\left(\frac{\omega }{c}\rho \right)}$

Comprobamos que cumple R(a)=0 y R(b)=0.

La solución completa es similar a la membrana circular, excepto en la parte radial, que ya hemos determinado

${\displaystyle \begin{array}{l}{\Psi }_{m,n}(\rho ,\phi ,t)=\left\{Y_m\left(\frac{{\omega }_{mn}}{c}b\right)J_m\left(\frac{{\omega }_{mn}}{c}\rho \right)-J_m\left(\frac{{\omega }_{mn}}{c}b\right)Y_m\left(\frac{\omega }{c}\rho \right)\right\}·\\ (C_n\cos (m\phi )+D_n\sin (m\phi ))·(A_n\cos ({\omega }_{m,n}t)+B_n\sin ({\omega }_{m,n}t))\\ m=\mathrm{0,1,2,...}n=\mathrm{1,2,3...}\end{array}}$

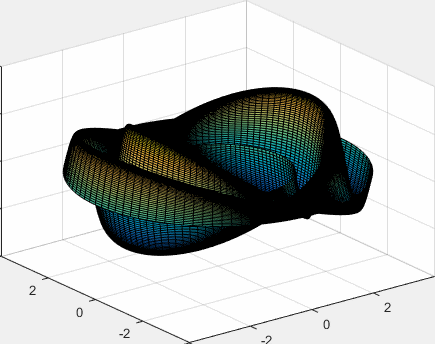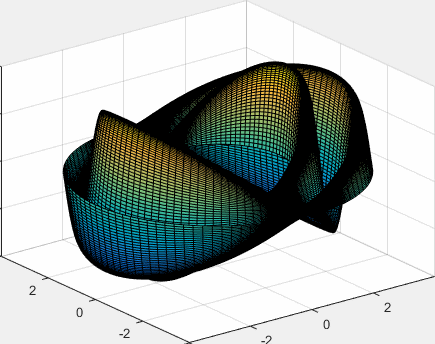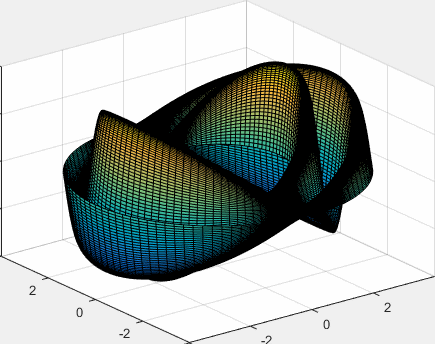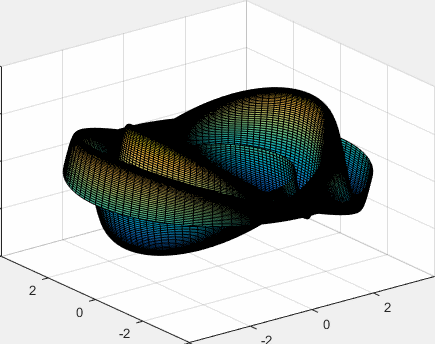
Representamos el modo de vibración de la membrana, para m=1 y para n=3, la raíz de la ecuación transcendente es ω₁₃/c=4.7222 (segunda fila, cuarta columna de la tabla)

${\displaystyle {\Psi }_{m,n}(\rho ,\phi ,t)=\left\{Y_m\left(\frac{{\omega }_{mn}}{c}b\right)J_m\left(\frac{{\omega }_{mn}}{c}\rho \right)-J_m\left(\frac{{\omega }_{mn}}{c}b\right)Y_m\left(\frac{\omega }{c}\rho \right)\right\}·\cos (m\phi )·\cos ({\omega }_{m,n}t)}$

alfa=4.722232462741136;  
a=4; %radios del anillo circular
b=2;
r=b:0.01:a;
ang=0:pi/50:2*pi;
[r,ang]=meshgrid(r,ang);
x=r.*cos(ang);
y=r.*sin(ang);
fichero = 'anillo_c.gif';
P=1;
m=1; %modo de vibración
n=3;
for t=0:P/20:P
    z = (bessely(m,alfa*b)*besselj(m,alfa*r)-besselj(m,alfa*b)*bessely(m,alfa*r))
.*cos(m*ang)*cos(2*pi*t/P);
    surf(x,y,z)
    xlabel('x')
    ylabel('y')
    zlabel('z')
    title('Vibración de anillo circular')
     
    frame=getframe;
    im = frame2im(frame);
    [imind,cm] = rgb2ind(im,256);
    if t==0
        imwrite(imind,cm,fichero,'gif','DelayTime',0,'loopcount',inf);
    else
        imwrite(imind,cm,fichero,'gif','DelayTime',0,'writemode','append');
    end
end

Referencias

M. M. Smirnov. Problemas de ecuaciones de la física matemática. Editorial Mir Moscú. 1976. Problema 113, enunciado, pág. 39, solución, págs. 105