Vamos a estudiar las oscilaciones transversales de una membrana rectangular de lados a y b.

La ecuación diferencial del movimiento ondulatorio es

${\displaystyle \frac{{\partial }^2\Psi }{\partial t^2}=c^2\left(\frac{{\partial }^2\Psi }{\partial x^2}+\frac{{\partial }^2\Psi }{\partial y^2}\right)}$

Condiciones iniciales y de contorno

Con las siguientes condiciones iniciales:

${\displaystyle t=0\{\begin{array}{l}\Psi (x,y\mathrm{,0})={\Psi }_0(x,y)\\ {\frac{\partial \Psi (x,y,t)}{\partial t}|}_{t=0}={\dot{\Psi }}_0(x,y)\end{array}}$

y de contorno:

La deformación Ψ(x,y,t) de la membrana en su contorno es nula para cualquier instante t

Modos de vibración

Supondremos que la solución de la ecuación diferencial del movimiento ondulatorio se puede expresar como producto

${\displaystyle \Psi (x,y,t)=\Phi (x,y)·T(t)}$

Introducciendo Ψ(x,y,t) en la ecuación diferencial del movimiento ondulatorio

${\displaystyle \begin{array}{l}\Phi (x,y)·\frac{d^{2}T}{d{t}^2}=c^2\left(T(t)\frac{{\partial }^2\Phi }{\partial x^2}+T(t)\frac{{\partial }^2\Phi }{\partial y^2}\right)\\ \frac{1}{T(t)}\frac{d^{2}T}{d{t}^2}=\frac{c^2}{\Phi (x,y)}\left(\frac{{\partial }^2\Phi (x,y)}{\partial x^2}+\frac{{\partial }^2\Phi (x,y)}{\partial y^2}\right)=-{\omega }^2\end{array}}$

Como el miembro izquierdo depende solamente de t y el derecho solamente de x e y, entonces, igualamos ambos a una constante que denominaremos -ω².

${\displaystyle \begin{array}{l}\frac{d^{2}T}{d{t}^2}+{\omega }^2·T=0\\ \frac{{\partial }^2\Phi }{\partial x^2}+\frac{{\partial }^2\Phi }{\partial y^2}+\frac{{\omega }^2}{c^2}\Phi =0\end{array}}$

Aplicamos el método de separación de variables a la segunda ecuación diferencial

${\displaystyle \begin{array}{l}\Phi (x,y)=H(x)·W(y)\\ W\frac{d^{2}H}{d{x}^2}+H\frac{d^{2}W}{d{y}^2}+\frac{{\omega }^2}{c^2}H·W=0\end{array}}$

Dividimos entre el producto H·W.

${\displaystyle \frac{1}{H}\frac{d^{2}H}{d{x}^2}=-\frac{1}{W}\left(\frac{d^{2}W}{d{y}^2}+\frac{{\omega }^2}{c^2}W\right)=-q^2}$

Como el miembro izquierdo depende solamente de x y el derecho solamente de y, entonces, igualamos ambos a una constante que denominaremos -q².

${\displaystyle \begin{array}{l}\frac{d^{2}H}{d{x}^2}+q^{2}H=0\\ \frac{d^{2}W}{d{y}^2}+\left(\frac{{\omega }^2}{c^2}-q^2\right)W=0\frac{d^{2}W}{d{y}^2}+r^{2}W=0\end{array}}$

Las dos ecuaciones diferenciales tienen soluciones conocidas

${\displaystyle \begin{array}{l}H(x)=C_x\cos \left(qx\right)+D_x\sin \left(qx\right)\\ W(y)=C_y\cos \left(ry\right)+D_y\sin \left(ry\right)\end{array}}$

Las condiciones de contorno imponen que los cuatro lados de la membrana estén fijos en todo momento:

${\displaystyle \begin{array}{l}\begin{array}{l}H(0)=0\\ H(a)=0\end{array}\}{C}_x=0\sin (qa)=0q=\frac{m\pi }{a}\\ \begin{array}{l}W(0)=0\\ W(b)=0\end{array}\}{C}_y=0\sin (rb)=0r=\frac{n\pi }{a}\\ {\Phi }_{mn}(x,y)=H_m(x)·W_n(y)=\sin \left(\frac{m\pi }{a}x\right)·\sin \left(\frac{n\pi }{b}y\right)m,n=\mathrm{1,2,3...}\end{array}}$

Para cada par de valores m y n tenemos la frecuencia del modo de vibración ω_m,n

${\displaystyle \frac{{\omega }^2}{c^2}=q^2+r^2{\omega }_{mn}^2=c^2\left(\frac{m^2{\pi }^2}{a^2}+\frac{n^2{\pi }^2}{b^2}\right)}$

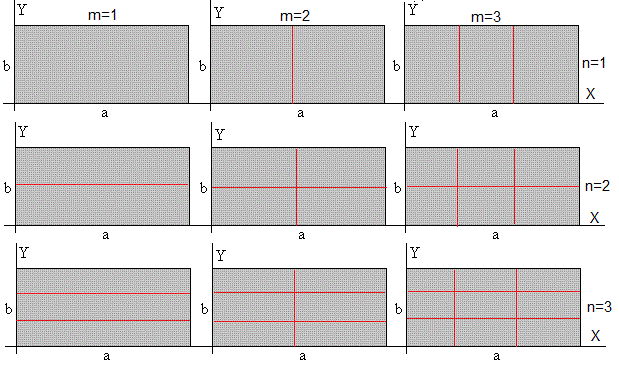
Los primeros modos de vibración de una membrana rectangular. Las líneas en color rojo señalan los nodos, los puntos de la membrana que no vibran para un modo particular. Más abajo, veremos la representación en 3D de los distintos modos (m,n) de vibración

m=2; %modo de vibración m,n
n=1;

%Dimensiones de la placa rectangular a=1, b=1
[x,y] = meshgrid(0:0.01:1);
z = sin(m*pi*x).*sin(n*pi*y);
surf(x,y,z)
xlabel('x')
ylabel('y')
zlabel('z')
title('Modos de vibración de una membrana rectangular')

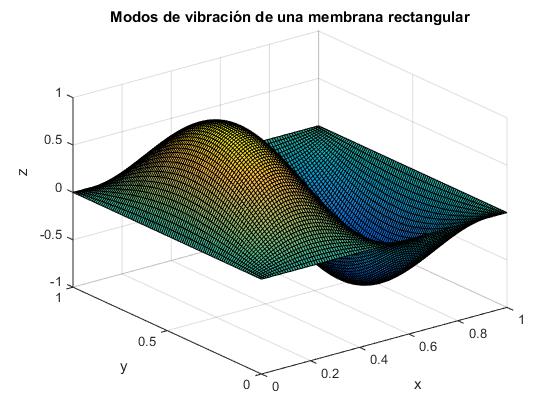
La solución de la ecuación diferencial dependiente del tiempo es tambien conocida

${\displaystyle T_{mn}(t)=A_{mn}\cos ({\omega }_{mn}t)+B_{mn}\sin ({\omega }_{mn}t)}$

La solución de la ecuación diferencial correspondiente al modo m, n de vibración de la membrana es

${\displaystyle \begin{array}{l}{\Psi }_{mn}(x,y,t)={\Phi }_{mn}(x,y)T_{mn}(t)=\\ \sin \left(\frac{m\pi }{a}x\right)·\sin \left(\frac{n\pi }{b}y\right)\left(A_{mn}\cos ({\omega }_{mn}t)+B_{mn}\sin ({\omega }_{mn}t)\right)\end{array}}$

En este script cremos una animación. Cada imagen generada (frame) se guarda en el vector F.

m=2; %modo de vibración m,n
n=1;
[x,y] = meshgrid(0:0.01:1);
j=0;
P=2/sqrt(m^2+n^2); %periodo de las oscilaciones
for t=0:P/20:P
    z = sin(m*pi*x).*sin(n*pi*y)*sin(2*pi*t/P);
    surf(x,y,z)
    xlabel('x')
    ylabel('y')
    zlabel('z')
    axis([0 1 0 1 -1 1]);
    j=j+1;
    F(j) = getframe;
end

Mediante el comando movie reproducimos la animación cuatro veces.

>> movie(F,4)

Alternativamente, podemos crear un fichero de imágenes GIF que muestran una animación

m=2; %modo de vibración m,n
n=1;
[x,y] = meshgrid(0:0.01:1);

P=2/sqrt(m^2+n^2); %periodo de las oscilaciones
fichero = 'placa_r.gif';
for t=0:P/20:P
    z = sin(m*pi*x).*sin(n*pi*y)*sin(2*pi*t/P);
    surf(x,y,z)
    xlabel('x')
    ylabel('y')
    zlabel('z')
    axis([0 1 0 1 -1 1]);
    
   frame=getframe;
    im = frame2im(frame);
    [imind,cm] = rgb2ind(im,256);
    if t==0
        imwrite(imind,cm,fichero,'gif','DelayTime',0,'loopcount',inf);
    else
        imwrite(imind,cm,fichero,'gif','DelayTime',0,'writemode',
'append');
    end
end

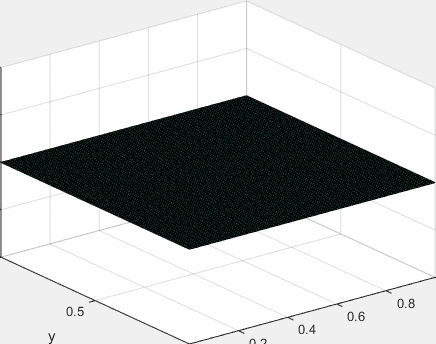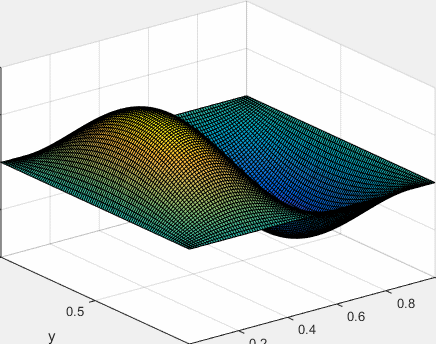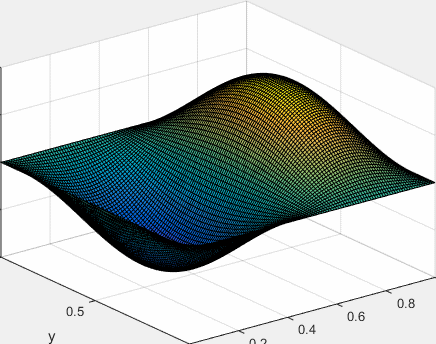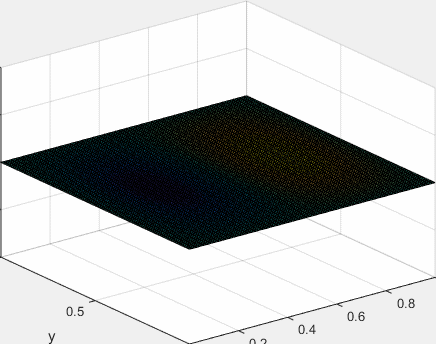
Solución completa

La solución general que satisface las condiciones de contorno es la superposición

${\displaystyle \begin{array}{l}\Psi (x,y,t)={\displaystyle \sum _{m=1}^{\infty }{\displaystyle \sum _{n=1}^{\infty }{\Psi }_{mn}(x,y,t)}}=\\ {\displaystyle \sum _{m=1}^{\infty }{\displaystyle \sum _{n=1}^{\infty }\sin \left(\frac{m\pi }{a}x\right)·\sin \left(\frac{n\pi }{b}y\right)\left(A_{mn}\cos ({\omega }_{mn}t)+B_{mn}\sin ({\omega }_{mn}t)\right)}}\end{array}}$

Esta ecuación describe todos los posibles modos de vibración de la membrana. La vibración particular que experimenta la membrana está únicamente determinada por las condiciones iniciales, que a su vez determinan los valores de las constantes A_mn y B_mn.

${\displaystyle \begin{array}{l}\Psi (x,y\mathrm{,0})={\Psi }_0(x,y)\\ \Psi (x,y\mathrm{,0})={\displaystyle \sum _{m=1}^{\infty }{\displaystyle \sum _{n=1}^{\infty }\sin \left(\frac{m\pi }{a}x\right)·\sin \left(\frac{n\pi }{b}y\right)A_{mn}}}\\ A_{mn}=\frac{4}{ab}{\displaystyle \underset{0}{\overset{a}{\int }}{\displaystyle \underset{0}{\overset{b}{\int }}{\Psi }_0(x,y)\sin \left(\frac{m\pi }{a}x\right)·\sin \left(\frac{n\pi }{b}y\right)dx·dy}}\\ {\frac{\partial \Psi (x,y,t)}{\partial t}|}_{t=0}={\dot{\Psi }}_0(x,y)\\ {\dot{\Psi }}_0(x,y)={\displaystyle \sum _{m=1}^{\infty }{\displaystyle \sum _{n=1}^{\infty }\sin \left(\frac{m\pi }{a}x\right)·\sin \left(\frac{n\pi }{b}y\right){\omega }_{mn}{B}_{mn}}}\\ B_{mn}=\frac{4}{ab{\omega }_{mn}}{\displaystyle \underset{0}{\overset{a}{\int }}{\displaystyle \underset{0}{\overset{b}{\int }}{\dot{\Psi }}_0(x,y)\sin \left(\frac{m\pi }{a}x\right)·\sin \left(\frac{n\pi }{b}y\right)dx·dy}}\end{array}}$

Consideremos una membrana cuadrada de lado a, que en el instante inicial t=0, tiene la forma

${\displaystyle {\psi }_0(x,y)=Axy(a-x)(a-y)}$

Representamos la función z=xy(a-x)(a-y)

a=1; %lado del cuadrado
x=0:0.02:a;
y=0:0.02:a;
[X,Y]=meshgrid(x,y);
Z=(X.*Y).*((a-X).*(a-Y));
mesh(X,Y,Z);
xlabel('X')
ylabel('Y')
zlabel('Z')
view(60,64)

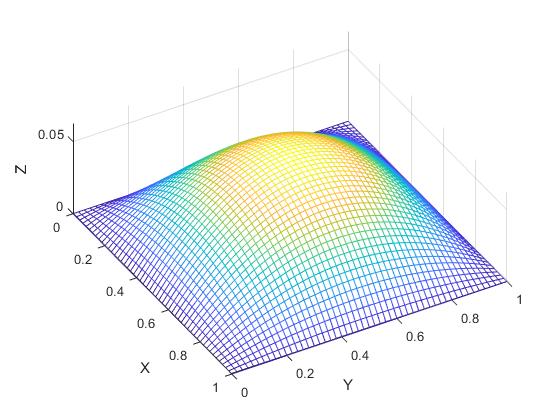
Como la membrana está en reposo en el instante t=0, los coeficientes B_mn=0. Calculamos los coeficientes A_mn

${\displaystyle \begin{array}{l}{A}_{mn}=\frac{4}{a^2}{\displaystyle \underset{0}{\overset{a}{\int }}{\displaystyle \underset{0}{\overset{a}{\int }}Axy(a-x)(a-y)\sin \left(\frac{m\pi }{a}x\right)}}\sin \left(\frac{n\pi }{a}y\right)dx·dy=\\ \frac{4A}{a^2}\left({\displaystyle \underset{0}{\overset{a}{\int }}x(a-x)\sin \left(\frac{m\pi }{a}x\right)dx}\right)\left({\displaystyle \underset{0}{\overset{a}{\int }}y(a-y)\sin \left(\frac{n\pi }{a}y\right)dy}\right)\end{array}}$

Integramos por partes

${\displaystyle \begin{array}{l}{\displaystyle \int x(a-x)\sin \left(\frac{m\pi }{a}x\right)dx}=-\frac{a}{m\pi }x(a-x)\cos \left(\frac{m\pi }{a}x\right)+\frac{a}{m\pi }{\displaystyle \int (a-2x)\cos \left(\frac{m\pi }{a}x\right)dx}=\\ -\frac{a}{m\pi }x(a-x)\cos \left(\frac{m\pi }{a}x\right)+\frac{a}{m\pi }\left\{\frac{a^2}{m\pi }\sin \left(\frac{m\pi }{a}x\right)-2\left(x\frac{a}{m\pi }\sin \left(\frac{m\pi }{a}x\right)+\frac{a^2}{m^2{\pi }^2}\cos \left(\frac{m\pi }{a}x\right)\right)\right\}=\\ -\frac{a}{m\pi }x(a-x)\cos \left(\frac{m\pi }{a}x\right)+\frac{a^3}{m^2{\pi }^2}\sin \left(\frac{m\pi }{a}x\right)-2\frac{a^2}{m^2{\pi }^2}x\sin \left(\frac{m\pi }{a}x\right)-2\frac{a^3}{m^3{\pi }^3}\cos \left(\frac{m\pi }{a}x\right)\end{array}}$

Evaluamos la integral entre los límites, superior a e inferior 0

${\displaystyle {\displaystyle \underset{0}{\overset{a}{\int }}x(a-x)\sin \left(\frac{m\pi }{a}x\right)dx}=-2\frac{a^3}{m^3{\pi }^3}\cos \left(m\pi \right)+2\frac{a^3}{m^3{\pi }^3}\cos \left(0\right)=\{\begin{array}{l}\mathrm{0,}m=\text{par}\\ 4\frac{a^3}{m^3{\pi }^3},m=\text{impar}\end{array}}$

Los coeficientes A_mn valen

${\displaystyle A_{mn}=\frac{4A}{a^2}\left({\displaystyle \underset{0}{\overset{a}{\int }}x(a-x)\sin \left(\frac{m\pi }{a}x\right)dx}\right)\left({\displaystyle \underset{0}{\overset{a}{\int }}y(a-y)\sin \left(\frac{n\pi }{a}y\right)dy}\right)=\frac{4A}{a^2}\{\begin{array}{l}\mathrm{0,}m,n=\text{par}\\ \left(4\frac{a^3}{m^3{\pi }^3}\right)\left(4\frac{a^3}{n^3{\pi }^3}\right),m,n=\text{impar}\end{array}}$

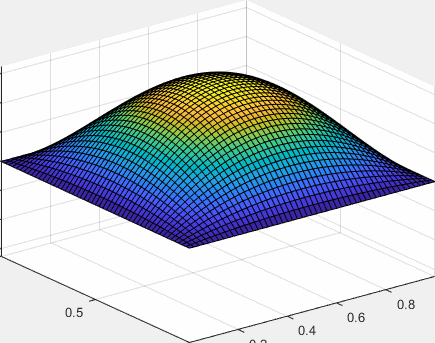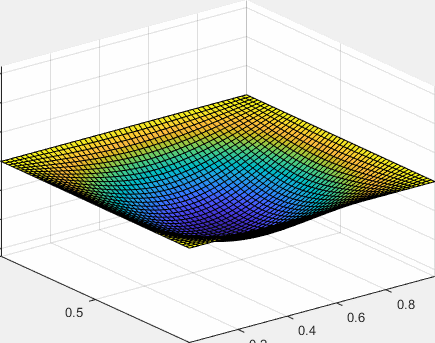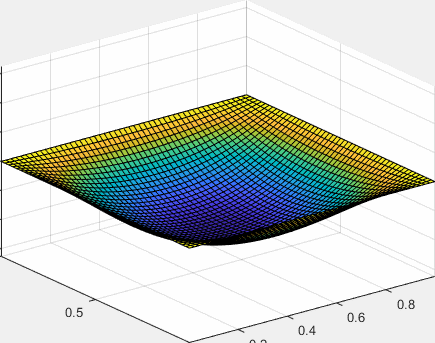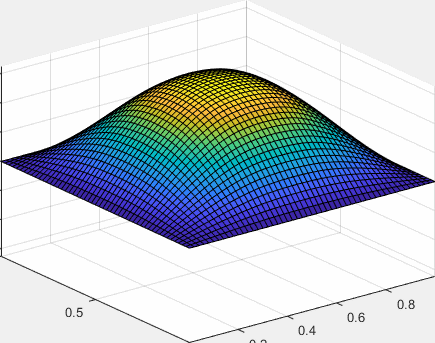
La solución de la ecuación diferencial del movimiento ondulatorio con las condiciones de contorno especificadas (bordes fijos) y la froma inicial de la membrana en reposo es

${\displaystyle \Psi (x,y,t)=\frac{64A{a}^4}{{\pi }^6}{\displaystyle \sum _{n=0}^{\infty }{\displaystyle \sum _{m=0}^{\infty }\frac{\sin \left(\frac{(2m+1)\pi }{a}x\right)\sin \left(\frac{(2n+1)\pi }{a}y\right)}{{\left(2m+1\right)}^3·{\left(2n+1\right)}^3}\cos \left(\frac{c\pi }{a}t\sqrt{{\left(2m+1\right)}^2+{\left(2n+1\right)}^2}\right)}}}$

Comprobamos que la forma inicial de la membrana se obtiene para t=0. Tomaremos n, m=10 términos del desarrollo en serie

function membrana_1
    a=1; %membrana cuadrada
    c=1; %velocidad ondas
    t=0; %forma inicial de la membrana
    
    x=0:0.02:a;
    y=0:0.02:a;
    [X,Y]=meshgrid(x,y);
    Z=onda(X,Y);
    mesh(X,Y,Z);
    xlabel('X')
    ylabel('Y')
    zlabel('Z')
    view(60,64)

    function z=onda(x,y)
        z=0;   
        for n=0:10
            for m=0:10
            z=z+sin((2*m+1)*x*pi/a).*sin((2*n+1)*y*pi/a)*
cos(c*pi*t*sqrt((2*m+1)^2+(2*n+1)^2)/a)/((2*m+1)^3*(2*n+1)^3);
            end
        end
        z=z*64*a^4/pi^6;
    end
end

La frecuencia angular mínima ${\omega }_{00}=\frac{c\pi }{a}\sqrt{2}$, para n, m=0, el periodo máximo es 2π/ω₀₀. Creamos un fichero GIF para producir una animación de la vibración de la membrana durante este tiempo

function membrana_2
    a=1; %membrana cuadrada
    c=1; %velocidad ondas
    tFin=sqrt(2); %tiempo final
    
    x=0:0.02:a;
    y=0:0.02:a;
    [X,Y]=meshgrid(x,y);
    fichero = 'placa_t.gif';
    for t=0:0.1:tFin
        z=onda(X,Y, t);
        surf(x,y,z)
        xlabel('x')
        ylabel('y')
        zlabel('z')
        axis([0 1 0 1 -0.065 0.065]);
        frame=getframe;
        im = frame2im(frame);
        [imind,cm] = rgb2ind(im,256);
        if t==0
            imwrite(imind,cm,fichero,'gif','DelayTime',0,'loopcount',tFin);
        else
            imwrite(imind,cm,fichero,'gif','DelayTime',0,'writemode','append');
        end
    end

    function z=onda(x,y, t)
        z=0;   
        for n=0:10
            for m=0:10
            z=z+sin((2*m+1)*x*pi/a).*sin((2*n+1)*y*pi/a)*
cos(c*pi*t*sqrt((2*m+1)^2+(2*n+1)^2)/a)/((2*m+1)^3*(2*n+1)^3);
            end
        end
        z=z*64*a^4/pi^6;
    end
end

Referencias

M. M. Smirnov. problemas de ecuaciones de la física matemática. Editorial Mir Moscú. 1976. Problema 122, enunciado, pág. 41, solución, pág. 111