Cañón de vapor de agua

El dispositivo consiste en un tubo cilíndrico de hierro de diámetro interno d=20 cm, longitud L=1 m, de masa m_t=20 kg, cerrado por su extremo izquierdo y que supondremos anclado al suelo para evitar retrocesos en el proceso de lanzamiento.

Se coloca dentro del tubo una bala de hierro de masa m_b=2 kg, que encaja perfectamente y sin rozamiento con las paredes del tubo y que está inicialmente a distancia a=50 cm de la base del tubo, creando una cámara hermética en la que previamente se han introducido 100 ml de agua. El resto de la cámara contiene aire y una cantidad inicialmente despreciable de vapor de agua.

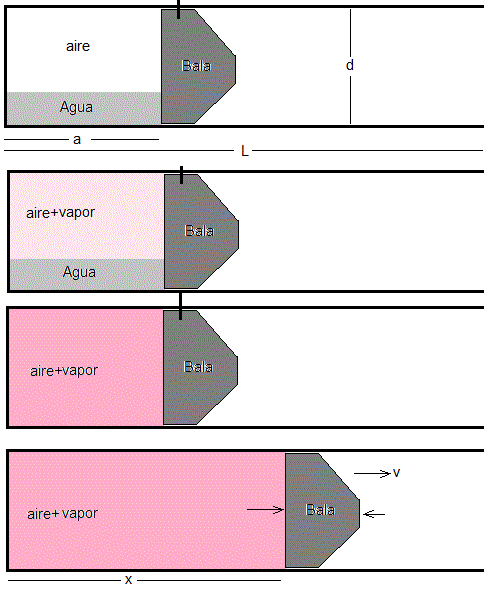
La temperatura inicial del cañón (tubo, bala, agua y aire) es T₁=20 °C y la presión inicial en la cámara es la atmosférica, p₁=1 atm. Se conecta al cañón una fuente de calor que le comunica una energía por unidad de tiempo k=5·10³ J/s.

Suponemos que todo el sistema se calienta de forma homogénea. Consideraremos en todo el problema que tanto el aire como el vapor de agua se comportan como gases ideales.

Datos

densidad del agua, ρ_a=1000 kg/m²
masa molecular del agua, M_a=0.018 kg/mol
masa molecular del aire, M_aire=0.029 kg/mol
presión atmosférica, 1 atm=101 325 Pa
temperatura del cero absoluto, T₀=- 273.15 °C=0 K
constante de los gases ideales, R=8.31 J/(kg·K)
calor latente de vaporización del agua, L= 40·10³ J/mol=2.22·10⁶ J/kg
calor específico del agua, c_a=4 180 J/(kg·K)
calor específico del hierro, c_Fe=450 J/(kg·K)
calor específico a volumen constante del vapor, c_v=1 410 J/(kg·K)
calor específico a volumen constante del aire, c_aire= 720 J/(kg·K)
coeficiente adiabático del vapor, γ=1.324
coeficiente adiabático del aire, γ=1.4

Estado del sistema para varias temperaturas

Primera figura, calculamos el número de moles de agua y el número de moles de aire que hay inicialmente dentro del cañón

Como hay 100 ml de agua su volumen será V_a=0.0001 m³, y su masa será m_a=0.1 kg. El número de moles es la masa dividida por la masa molecular:

$n_{a} = \frac{m_{a}}{M_{a}} = \frac{0.1}{0.018} = 5.56 moles$

El volumen de la cámara es V_total=π(d/2)²a=0.0157 m³. El volumen que ocupa el aire es V_aire=V_total-V_a=0.0157-0.0001=0.0156 m³ que es prácticamente el volumen total. La temperatura inicial es 20 °C

$n_{a i r e} = \frac{p_{1} V_{a i r e}}{R T_{1}} = \frac{101325 \cdot 0.0156}{8.31 \cdot (273.15 + 20)} = 0.65 moles$

La densidad del aire es

$ρ_{a i r e} = \frac{m_{a i r e}}{V_{a i r e}} = \frac{n_{a i r e} M_{a i r e}}{V_{a i r e}} = \frac{0.65 \cdot 0.029}{0.0156} = 1.2 \frac{kg}{m^{3}}$

Segunda figura, elevamos la temperatura a T₂=150 °C

La presión de vapor de agua p_v se relaciona con la temperatura T por medio de la ecuación de Clausius-Clapeyron

$p_{v} = p_{v_{0}} \exp (\frac{L}{R} (\frac{1}{T_{0}} - \frac{1}{T}))$

donde p_v está expresada en Pa y T en K, la constante L es el calor latente de vaporización del agua y R es la constante de los gases ideales. (Se comprueba que a 100 °C la presión de vapor es 1 atm.). La presión de vapor a 150 °C es

$p_{v 2} = 101325 \exp (\frac{40 \cdot 10^{3}}{8.31} (\frac{1}{273.15 + 100} - \frac{1}{273.15 + 150})) = 4.59 atm$

Aunque ya se ha evaporado algo de agua, ésta ocupa un volumen despreciable y podemos considerar que el volumen que ocupa el aire y el vapor es prácticamente el mismo que el inicial. La presión del aire es

$p_{a i r e 2} = \frac{n_{a i r e} R T_{2}}{V_{a i r e}} = \frac{0.65 \cdot 8.31 \cdot (273.15 + 150)}{0.0156} = 1.44 atm$

La presión total dentro de la cámara será la suma de la presión del aire y la presión de vapor:

p_total=p_aire2+p_v2=1.44+4.59=6.043 atm

El número de moles de vapor es

$n_{v 2} = \frac{p_{v 2} V_{a i r e}}{R T_{2}} = \frac{(101325 \cdot 4.59) \cdot 0.0156}{8.31 \cdot (273.15 + 150)} = 2.06 moles$

Por tanto, quedan 5.56-2.06=3.5 moles de agua sin evaporar

Tercera figura, elevamos la temperatura a T₃ hasta que todo el agua se convierte en vapor

Seguimos calentando hasta una temperatura T₃, justo a la cual toda el agua líquida se ha evaporado y ya sólo hay vapor en la cámara del cañón.

Cuando se ha evaporado toda el agua, el número de moles de vapor es igual al número inicial de moles de agua es decir, n_v=n_a=5.56 moles. El vapor ocupará todo el volumen de la cámara, V_total. Según la ecuación de los gases ideales, la presión del vapor y la temperatura cumplirán

$\begin{array}{l} p_{v 3} = \frac{n_{v} R T_{3}}{V_{t o t a l}} = \frac{5.56 \cdot 8.31}{0.0157} T_{3} = 2943 \cdot T_{3} Pa \\ p_{v 3} = 101325 \exp (\frac{40 \cdot 10^{3}}{8.31} (\frac{1}{373.15} - \frac{1}{T_{3}})) = 4.05 \cdot 10^{10} \exp (- \frac{4813.5}{T_{3}}) Pa \end{array}$

Resolvemos la ecuación transcendente

$2943 \cdot T_{3} = 4.05 \cdot 10^{10} \exp (- \frac{4813.5}{T_{3}})$

hold on
fplot(@(t) 2943*(t+273.15)/101325,[150, 250])
fplot(@(t) 4.05e10*exp(-4813.5./(t+273.15))/101325,[150, 250])
f=@(t) 2943*(t+273.15)-4.05e10*exp(-4813.5/(t+273.15));
T3=fzero(f,[150,250]);
pv=2943*(T3+273.15)/101325;
plot(T3,pv,'ro','markersize',3,'markerfacecolor','r')
line([T3,T3],[0,pv],'lineStyle','--')
line([150,T3],[pv,pv],'lineStyle','--')
disp([T3, 2943*(T3+273.15)])
hold off
grid on
xlabel('t')
ylabel('p_v (atm)')
title('Solución gráfica')

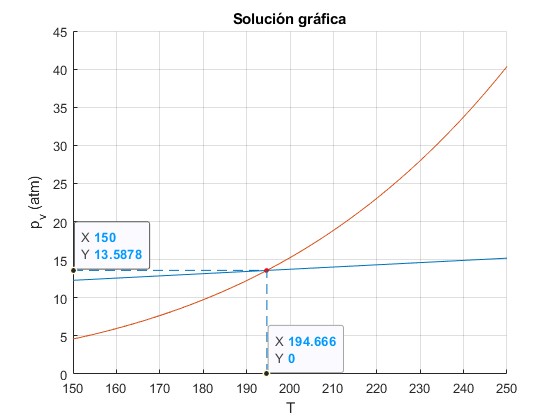
 194.6657   13.5878

La temperatura buscada T₃=194.7 °C≈195 °C y la presión de vapor p_v3=13.6 atm

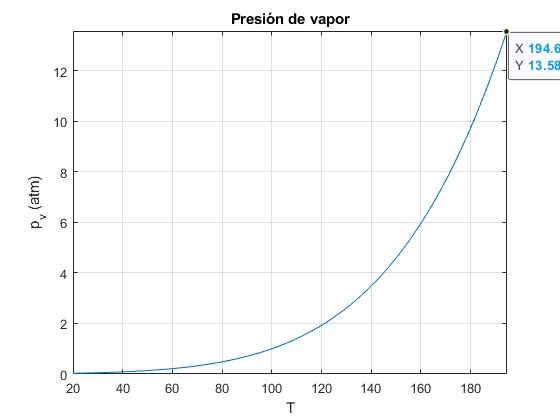
Representamos la presión de vapor p_v en función de la temperatura en el intervalo 20 a 194.6 °C

pv=@(t) exp(40e3*(1/373.15-1./(t+273.15))/8.31);
fplot(pv,[20,194.6])
grid on
xlabel('t')
ylabel('p_v (atm)')
title('Presión de vapor')

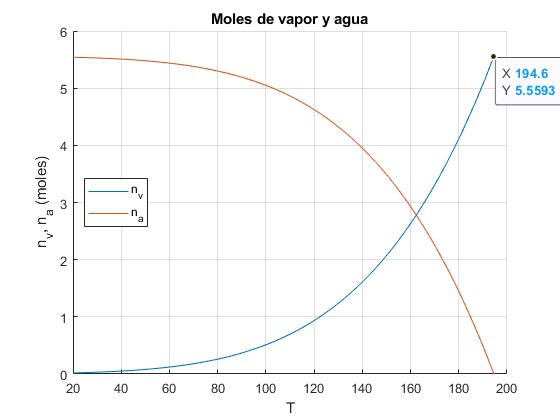
Representamos el número de moles de vapor n_v y de agua n_a en función de la temperatura en el intervalo 20 a 194.6 °C

$\begin{array}{l} p_{v} = \frac{n_{v} R T}{V_{t o t a l} - (n_{a} - n_{v}) M_{a} / ρ_{a}} = \frac{n_{v} \cdot 8.31 \cdot T}{0.0157 - (5.56 - n_{v}) 0.018 / 1000} \\ n_{v} = \frac{p_{v} (0.0157 - 5.56 \cdot 0.018 / 1000)}{8.31 \cdot T - p_{v} \cdot 0.018 / 1000} \\ n_{a} + n_{v} = 5.56 \end{array}$

pv=@(t) 101325*exp(40e3*(1/373.15-1./(t+273.15))/8.31);
nv=@(t) pv(t).*(0.0157-5.56*0.018/1000)./(8.31*(t+273.15)-
pv(t)*0.018/1000);
hold on
fplot(nv,[20,194.6]) %moles de vapor
na=@(t) 5.56-nv(t);
fplot(na,[20,194.6]) %moles de agua
hold off
grid on
xlabel('t')
ylabel('n_v, n_a (moles)')
legend('n_v','n_a', 'Location','best')
title('Moles de vapor y agua')

Se calienta aún más hasta alcanzar la temperatura de T₄=300 °C

La presión parcial del vapor es

$p_{v 4} = \frac{n_{v} R T_{4}}{V_{t o t a l}} = \frac{5.56 \cdot 8.31 \cdot (273.15 + 300)}{0.0157} = 16.6 atm$

La presión parcial del aire es

$p_{a i r e 4} = \frac{n_{a i r e} R T_{4}}{V_{t o t a l}} = \frac{0.65 \cdot 8.31 \cdot (273.15 + 300)}{0.0157} = 1.9 atm$

La presión total es p_t=16.6+1.9=18.5 atm

La presión en función de la temperatura

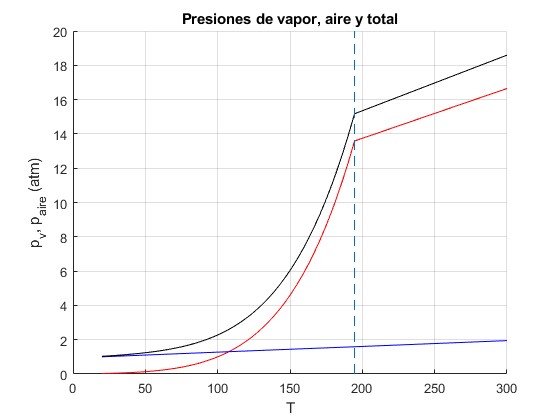
Representamos la presión parcial de vapor p_v (en atm) en función de la temperatura (color rojo) en el intervalo 20 a 300 °C

$\begin{array}{l} p_{v} = 101325 \exp (\frac{40 \cdot 10^{3}}{8.31} (\frac{1}{373.15} - \frac{1}{273.15 + t})), 20 < t < 194.6 \\ p_{v} = \frac{n_{a} R T}{V_{t o t a l}} = \frac{5.56 \cdot 8.31 \cdot (t + 273.15)}{0.0157}, 194.6 < t < 300 \end{array}$

Representamos la presión parcial del aire p_aire (en atm) en función de la temperatura (color azul) en el intervalo 20 a 300 ºC

$\begin{array}{l} p_{a i r e} = \frac{n_{a i r e} R T}{V_{t o t a l} - V_{a}} = \frac{0.65 \cdot 8.31 \cdot (t + 273.15)}{0.0157 - (5.56 - n_{v}) \cdot 0.018 / 1000}, 20 < t < 194.6 \\ p_{a i r e} = \frac{n_{a i r e} R T}{V_{t o t a l}} = \frac{0.65 \cdot 8.31 \cdot (t + 273.15)}{0.0157}, 194.6 < t < 300 \end{array}$

El número de moles de vapor n_v en función de la temperatura se ha dterminado en el punto anterior

La presión total (color negro) es la suma de las dos presiones parciales

pv_1=@(t) exp(40e3*(1/373.15-1./(t+273.15))/8.31);
nv=@(t) 101325*pv_1(t).*(0.0157-5.56*0.018/1000)./
(8.31*(t+273.15)-101325*pv_1(t)*0.018/1000);
hold on
p_aire_1=@(t) 0.65*8.31*(273.15+t)./
((0.0157-(5.56-nv(t))*0.018/1000)*101325);
fplot(pv_1,[20,194.6],'color','r') %presión de vapor
fplot(p_aire_1,[20,194.6],'color','b') %presión de aire
p1=@(t) pv_1(t)+p_aire_1(t);
fplot(p1,[20,194.6],'color','k') %presión total

pv_2=@(t) 5.56*8.31*(t+273.15)/(0.0157*101325);
p_aire_2=@(t) 0.65*8.31*(273.15+t)/(0.0157*101325);
fplot(pv_2,[194.6,300],'color','r') %presión de vapor
fplot(p_aire_2,[194.6,300],'color','b') %presión de aire
p2=@(t) pv_2(t)+p_aire_2(t);
fplot(p2,[194.6,300],'color','k') %presión total
line([194.6,194.6],[0,20],'lineStyle','--')
hold off
grid on
xlabel('T')
ylabel('p_v, p_{aire} (atm)')
title('Presiones de vapor, aire y total')

Movimiento de la bala

Figura 4, se libera el pasador y la bala se puede mover sin fricción a lo largo del tubo

Esta presión es mucho mayor que la atmosférica, por eso, cuando se suelte el pasador, la bala del cañón comenzará a acelerarse hacia la derecha. El proceso de expansión es muy rápido supondremos que es un adiabático, pV^γ=cte. Las presiones parciales y la total de la cámara cuando la bala está a distancia x será

$\begin{array}{l} p_{v} (x) = {(\frac{V_{t o t a l}}{V (x)})}^{γ} p_{v 4} = 16.6 {(\frac{π {(\frac{d}{2})}^{2} a}{π {(\frac{d}{2})}^{2} x})}^{1.324} = 16.6 {(\frac{0.5}{x})}^{1.324} = \frac{6.63}{x^{1.324}} atm= \frac{6.7 \cdot 10^{5}}{x^{1.324}} Pa \\ p_{a i r e} (x) = {(\frac{V_{t o t a l}}{V (x)})}^{γ} p_{a i r e 4} = 1.9 {(\frac{π {(\frac{d}{2})}^{2} a}{π {(\frac{d}{2})}^{2} x})}^{1.4} = 1.9 {(\frac{0.5}{x})}^{1.4} = \frac{0.38}{x^{1.4}} atm= \frac{3.85 \cdot 10^{4}}{x^{1.4}} Pa \\ p (x) = p_{a i r e} (x) + p_{v} (x) \end{array}$

Para x=L=1 m, la presión total es p(L)=7.01 atm

La fuerza sobre la bala cuando se encuentra a una distancia x, es (p-p_atm)π(d/2)²

$F (x) = (\frac{6.7 \cdot 10^{5}}{x^{1.324}} + \frac{3.85 \cdot 10^{4}}{x^{1.4}} - 101325) π {(\frac{0.2}{2})}^{2}$

La ecuación del movimiento

$\begin{array}{l} m_{b} \frac{d^{2} x}{d t^{2}} = F (x) \\ m_{b} \frac{d v}{d t} = F (x) \\ m_{b} \frac{d v}{d x} \frac{d x}{d t} = F (x) \\ m_{b} v \frac{d v}{d x} = F (x) \end{array}$

Integramos

$\begin{array}{l} \int_{0}^{v} v \cdot d v = \frac{π \cdot {0.1}^{2}}{2} \int_{0.5}^{1} (\frac{6.7 \cdot 10^{5}}{x^{1.324}} + \frac{3.85 \cdot 10^{4}}{x^{1.4}} - 101325) d x \\ \frac{1}{2} v^{2} = \frac{π \cdot {0.1}^{2}}{2} {- 6.7 \cdot 10^{5} \frac{x^{- 0.324}}{0.324} - 3.85 \cdot 10^{4} \frac{x^{- 0.4}}{0.4} - 101325 x}_{0.5}^{1} \\ v = 125.43 m/s \end{array}$

Si solamente tuviésemos en cuenta la fuerza que ejerce la presión de vapor

$\begin{array}{l} \int_{0}^{v} v \cdot d v = \frac{π \cdot {0.1}^{2}}{2} \int_{0.5}^{1} \frac{6.7 \cdot 10^{5}}{x^{1.324}} d x \\ \frac{1}{2} v^{2} = \frac{π \cdot {0.1}^{2}}{2} {- 6.7 \cdot 10^{5} \frac{x^{- 0.324}}{0.324}}_{0.5}^{1} \\ v = 127.9 m/s \end{array}$

Un valor similar

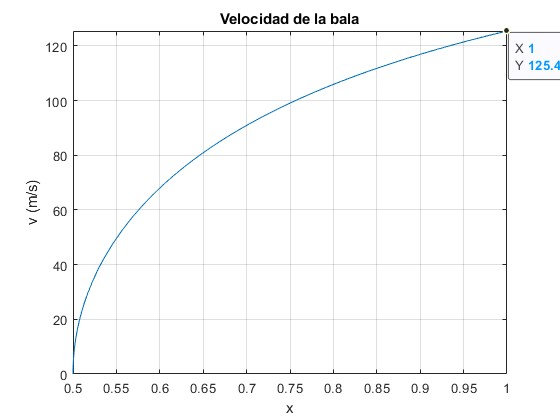
Representamos la velocidad de la bala v en función de su posición x en el tubo en el intervalo 0.5 (parte del reposo) a 1 m

f=@(x) -6.7e5*x.^-0.324/0.324-3.85e4*x.^-0.4/0.4-101325*x;
v=@(x) 0.1*sqrt(pi*(f(x)-f(0.5)));
fplot(v,[0.5,1])
grid on
xlabel('x')
ylabel('v (m/s)')
title('Velocidad de la bala')

Resolvemos por el procedimiento numérico ode45 de MATLAB la ecuación diferencial del movimiento de la bala

$\frac{d^{2} x}{d t^{2}} = \frac{1}{2} (\frac{6.7 \cdot 10^{5}}{x^{1.324}} + \frac{3.85 \cdot 10^{4}}{x^{1.4}} - 101325) π {(\frac{0.2}{2})}^{2}$

con las condiciones iniciales, para t=0, x=0.5 m, dx/dt=0 (parte del reposo)

function canon_5
    opts=odeset('events',@stop_planeta);
    f=@(t, x) [x(2);(6.7e5/x(1)^1.324+3.85e4/x(1)^1.4-101325)*pi*0.01/2];
    [t,x]=ode45(f,[0,1],[0.5,0],opts);
    plot(t,x(:,1))
    grid on
    xlabel('t(s)')
    ylabel('x (m)')
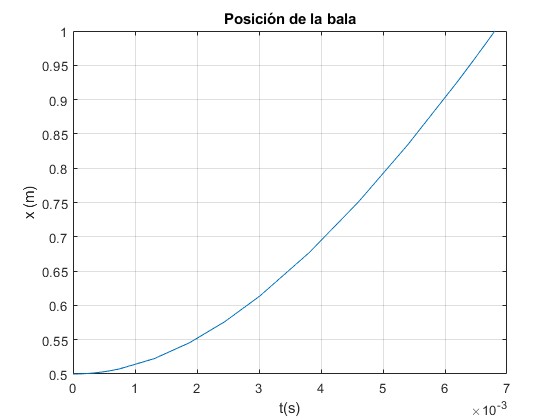
    title('Posición de la bala')
    disp([t(end),x(end,2)])

    function [value,isterminal,direction]=stop_planeta(~,x)
        value=x(1)-1;
        isterminal=1;  
        direction=1; 
    end
end

 0.0068  125.4270

El tiempo que tarda la bala en salir del cañón x=1 m, es t=0.0068 s, alcanzando una velocidad de 125.4 m/s, que ya hemos calculado previamente

Calor suministrado al sistema

Calculamos el calor total empleado para aumentar la temperatura de T₁=20 °C a T₄=300 °C

Supondremos que, aunque la evaporación es gradual, toda el agua permanece líquida hasta T₃=195 °C. Supondremos también que el aire y el vapor experimentan procesos a volumen constante.

Calentamiento de una masa de hierro m_t+m_b=22 kg de T₁ a T₄

Q_Fe=(m_t+m_b)c_Fe(T₄-T₁)=22·450(300-20)=2772 kJ

Calentamiento de una masa de aire m_aire=0.65·0.029=0.0189 kg de de T₁ a T₄

Q_aire=m_aire·c_aire(T₄-T₁)=0.65·0.029·720(300-20)=3.8 kJ

Calentamiento de una masa de agua m_a=0.1 kg desde T₁ a T₄

Aunque la evaporación es gradual, como aproximación, supondremos que toda el agua permanece líquida hasta T₃

Q_a=m_a·c_a(T₃-T₁)=0.1·4180(195-20)=73.2 kJ

Calentamiento de una masa de vapor m_v=0.1 kg desde T₃ a T₄

Q_v=m_v·c_v(T₃-T₃)=0.1·1410(300-195)=14.8 kJ

Vaporización de una masa de agua m_a=0.1 kg

Q_L=m_a·L=0.1·2.22·10⁶=222 kJ

El calor total necesario para llevar el sistema hasta desde T₁ a T₄

Q=Q_Fe+Q_aire+Q_a+Q_L=3086 kJ

La fuente de calor ha estado encendida un tiempo t=Q/k=3086/5=10.3 min

Referencias

Problemas de las Olimpiadas Nacionales. Problema 1.-Architronito de Arquímedes. OEF 2023 (Lugo)