Medida de la presión de vapor del agua (I)
La presión de vapor
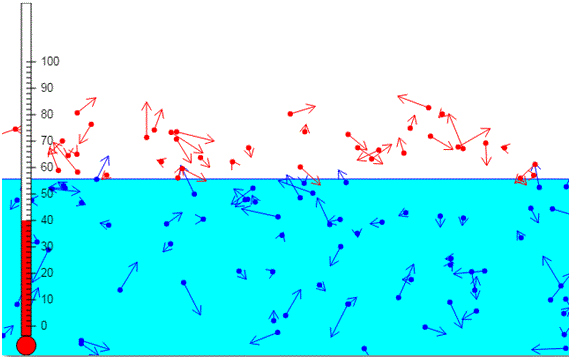
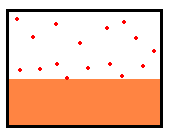
Si se calienta un líquido se incrementa la energía cinética media de sus moléculas. Las moléculas cuya energía cinética es más elevada y que están cerca de la superficie del líquido escaparán y darán lugar a la fase de vapor
Si el líquido está contenido en un recipiente cerrado, algunas moléculas del vapor seguirán el camino inverso chocando con la superficie del líquido e incorporándose a la fase líquida.
Se establece un equilibrio dinámico, cuando el número de moléculas que se escapan del líquido sea igual (en valor medio) al número de moléculas que se incorporan al mismo. Decimos entonces, que tenemos vapor saturado a la temperatura T y la presión parcial que ejercen las moléculas de vapor a esta temperatura se denomina presión de vapor Pv.
La presión de vapor de una sustancia depende solamente de la temperatura y no del volumen; esto es, un recipiente que contiene líquido y vapor en equilibrio a una temperatura fija, la presión es independiente de las cantidades relativas de líquido y de vapor presentes.
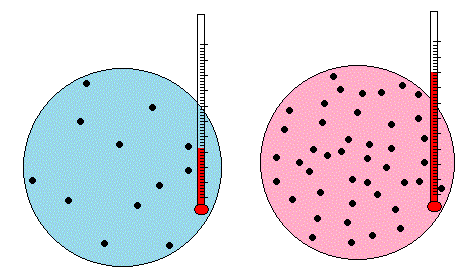
Al incrementarse la temperatura del líquido, un mayor número de moléculas tiene energía cinética suficiente para escapar de la fase líquida, el flujo de moléculas que escapan es mayor y por tanto, en el equilibrio, la presión de vapor saturado será aún mayor.
La presión de vapor a 273.15 K es Pv= 6.11 hPa que es una cantidad muy pequeña frente a la presión total de alrededor de 1000 hPa. A 25° C la presión de saturación Pv se incrementa cinco veces.
La temperatura de ebullición es aquella para la cual, la presión de vapor es igual a la presión exterior. La presión de vapor del agua es igual a una atmósfera a la temperatura de 100ºC
La ecuación de Clausius-Clapeyron
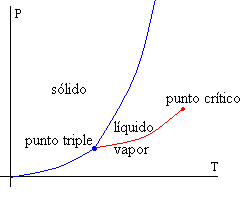
La evaporación del agua es un ejemplo de cambio de fase de líquido a vapor.
La ecuación de Clapeyron deriva del equilibrio entre dos fases de una sustancia, en dicha situación la entropía es máxima. En el artículo de Koutsoylannis se deriva esta ecuación llegando a la expresión
T0=273.16 K es la temperatura del punto triple del agua y Pv0=6.11657 hPa es la presión de vapor a dicha temperatura.
tt=linspace(-40,50,200);
f=@(t) 6.11657*exp(24.921*(1-273.16./(t+273.16))).*(273.16./(t+273.16)).^5.06;
semilogy(tt,f(tt))
grid on
xlabel('t ºC')
ylabel('P_v (hPa)')
title('Presión de vapor')
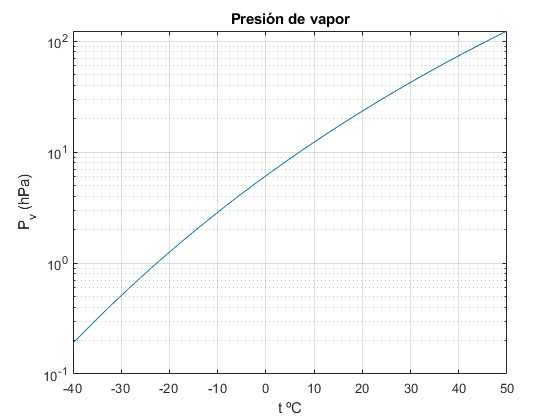
Existen otras fórmulas, en el artículo de Huang se proporciona las fórmulas de la presión de vapor del agua para el agua y para el hielo
tt=-100:20:0; f=@(t) exp(43.494-6545.8./(t+278))./(t+868).^2; Pv=f(tt); disp([tt',Pv']) tt=20:20:100; tt=[0.01,tt]; f=@(t) exp(34.494-4924.99./(t+237.1))./(t+105).^1.57; Pv=f(tt); disp([tt',Pv'])
| Temperatura °C | Presión de vapor (Pa) |
|---|---|
| -100 | 0.0014 |
| -80 | 0.0548 |
| -60 | 1.0814 |
| -40 | 12.841 |
| -20 | 103.23 |
| 0 | 611.29 |
| 0.01 | 611.69 |
| 20 | 2 339.32 |
| 40 | 7 384.93 |
| 60 | 19 946.1 |
| 80 | 47 415.0 |
| 100 | 101 417 |
A 100° C la presión de vapor coincide con la presión atmosférica, se produce la ebullición
Deducción cualitativa
Suponiendo que la fase vapor es un gas ideal y que el volumen molar del líquido es despreciable comparado con el volumen molar de gas, se llega a la denominada ecuación de Clausius-Clapeyron que nos proporciona la presión de vapor del agua Pv en función de la temperatura T, suponiendo además, que la entalpía L de vaporización es independiente de la temperatura (al menos en un determinado intervalo)
donde C es una constante
Una derivación sencilla de la ecuación de Clausius- Clapeyron es la siguiente
El primer principio de la Termodinámica
ΔU=Q-W
siendo Q el calor absorbido (Q>0) por el sistema y W el trabajo realizado por el sistema (W>0 si el sistema aumenta su volumen).
Supongamos que una cantidad de calor Q=Li convierte un mol de líquido en un mol de vapor sin cambio de volumen, entonces
ΔU=Q=Li
Sin embargo, durante el proceso de vaporización hay un cambio de volumen, un mol de líquido Vl ocupa menos volumen que un mol de vapor Vv a la misma presión P y temperatura T. El trabajo realizado por el sistema es W=P(Vv-Vl)
El calor que tenemos que suministrar es
Q=L= ΔU+W=Li+ P(Vv-Vl)
L se define como el calor latente o entalpía de vaporización, es decir, el calor necesario para que se evapore un mol de líquido a una presión constante P y a la temperatura T.
Normalmente Vv>> Vl y suponiendo que el vapor se comporta como un gas ideal, tendremos para un mol de vapor
PV=RT
Finalmente, tendremos la relación
L=Li+RT
Si consideramos que la función de distribución de Boltzmann se aplica al mecanismo de la evaporación
donde nv y nl son el número de moles en la unidad de volumen en el vapor y en el líquido, respectivamente a la temperatura absoluta T, y Li es el valor medio por mol de sustancia de la diferencia entre la energía potencial de las moléculas en su fase de vapor y en su fase líquida.
Esta ecuación nos dice que nv y por tanto, la presión de vapor Pv, se incrementan rápidamente con la temperatura absoluta T.
Derivando esta ecuación respecto de T, suponiendo que nl es independiente de T.
Si el vapor se comporta como un gas ideal Pv=nvRT o bien, ln nv=ln Pv-ln(RT)
Derivando esta expresión respecto de T
o bien,
Esta es una de las formas de la famosa ecuación de Clausius-Clapeyron que proporciona la pendiente de la curva, en el diagrama P-T (figura al principio de esta sección), de coexistencia de las fases líquida y de vapor en equilibrio.
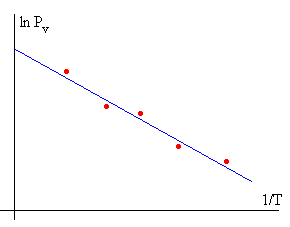
El calor latente L varía con la temperatura T, pero podemos suponerlo constante en un intervalo dado de temperaturas. Integrando la ecuación diferencial, obtenemos
De este modo, haciendo una representación gráfica de ln Pv en función de la inversa de la temperatura T, la pendiente de la recta nos proporciona el valor medio del calor latente de vaporización L en un intervalo dado de temperaturas.
Experimento
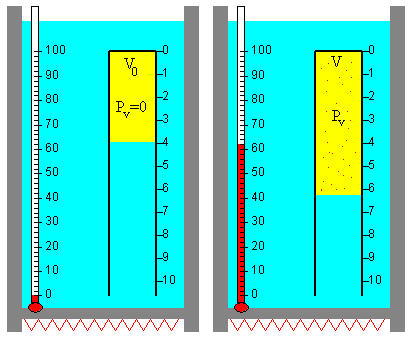
Se coloca un tubo de vidrio de 10 cm3 boca abajo en un recipiente lleno de agua, tal como se muestra en la figura.
A la temperatura T0=0º C, supondremos que el tubo solamente contiene un volumen V0 de aire y que la cantidad de vapor es despreciable. La presión del aire es la presión atmosférica P0 y se desprecia la presión producida por la columna de agua por encima de la superficie de separación entre el agua y el aire en el tubo invertido.
Suponiendo que el aire es un gas ideal, el número de moles na de aire contenido en el volumen V0 es
La cantidad de aire en el tubo na no cambia durante la experiencia. A la temperatura T, el tubo contiene una mezcla de aire y vapor de agua, sus presiones parciales son Pa y Pv, respectivamente, de modo que
Midiendo el volumen V de la mezcla de aire y vapor de agua en el tubo invertido determinamos la presión Pv de vapor del agua. Si representamos
- en el eje vertical el logaritmo neperiano de la presión de vapor, lnPv
- en el eje horizontal la inversa de la temperatura 1/T
obtendremos un conjunto de puntos que se sitúa sobre una recta verificándose la ecuación de Clausius-Clapeyron. La pendiente de la recta de ajuste L/R nos permite calcular la entalpía de vaporización L.
Actividades
De acuerdo a los datos proporcionados en el primer artículo citado en las referencias, se ha fijado
-
La presión atmosférica P0=100690 Pa
-
El volumen que ocupa el aire a la temperatura de T0=273.15 K es V0=3.95 cm3, a esta temperatura se supone que la cantidad de vapor de agua es muy pequeña.
-
En la simulación, los valores “experimentales” de la presión de vapor Pv se obtienen para cada temperatura T en K a partir de la ecuación de Antoine
Se pulsa el botón titulado Nuevo
-
Se observa el aire en el tubo de vidrio invertido dentro del recipiente de agua a la temperatura de T0=0º C=273.15 K.
Se introduce
-
La temperatura T en ºC actuando en el control titulado Temperatura en el intervalo especificado.
Se pulsa el botón titulado Calcula
Se mide el volumen V de la mezcla de aire y vapor de agua y se calcula la presión de vapor a partir de la ecuación
Se representa,
- en el eje vertical el logaritmo neperiano de la presión de vapor, lnPv
- en el eje horizontal la inversa de la temperatura 1/T
Se verifica la ecuación de Clausius-Clapeyron.
Ejemplo
Se han tomado los siguientes datos de la simulación:
| Temperatura | 0 | 50 | 55 | 60 | 65 | 70 | 75 |
|---|---|---|---|---|---|---|---|
| Volumen | 3.97 | 5.33 | 5.62 | 6.00 | 6.50 | 7.18 | 8.15 |
T=(50:5:75)+273;
V=[5.33,5.62,6.00,6.50,7.18,8.15];
Pv=100690*(1-3.97*T./(273*V));
plot(1./T, log(Pv),'ro','markersize',3,'markeredgecolor','r',
'markerfacecolor','r')
grid on
xlabel('1/T')
ylabel('log(P_v)')
title('Presión de vapor')
En el menú seleccionamos Tools/Basic Fitting, aparece un cuadro de diálogo donde marcamos la casilla linear en Plot fits. A continuación, pulsamos la flecha hacia la derecha --> para mostrar los coeficientes p1 y p2 del polinomio (recta) y=p1*x+p2 de ajuste.
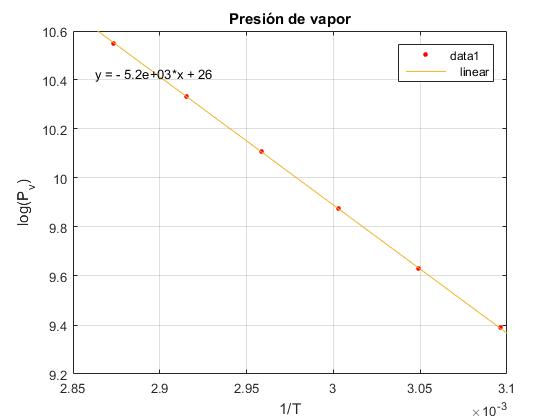
La pendiente p1 de la recta es L/R=5233, y el valor de la entalpía de vaporización L=5233·8.3143=43 509 J/mol
Referencias
Gesari S., Irigoyen B., Juan A. An experiment on the liquid-vapor equilibrium for water. Am. J. Phys. 64 (9) September 1996, pp. 1165-1168
Bligh P. H., Haywood R. Latent heat- its meaning and measurement. Eur. J. Phys. 7(1986) pp. 245-251.
Demetris Koutsoyiannis. Clausius–Clapeyron equation and saturation vapour pressure: simple theory reconciled with practice. Eur. J. Phys. 33 (2012) pp. 295–305
Jianhua Huang. A Simple Accurate Formula for Calculating Saturation Vapor Pressure of Water and Ice. Journal of Applied Meteorology and Climatology. Vol. 57. June 2018, pp. 1265-1272

