Experimento de Joule. Equivalente mecánico del calor
Un recipiente aislado térmicamente contiene una cierta cantidad de agua, con un termómetro para medir su temperatura, un eje con unas paletas que se ponen en movimiento por la acción de una pesa, tal como se muestra en la figura.
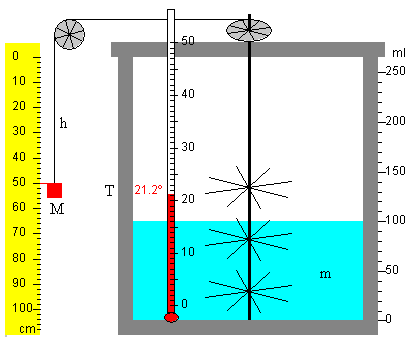
La versión original del experimento, consta de dos pesas iguales que cuelgan simétricamente del eje.
La pesa, que se mueve con velocidad prácticamente constante, pierde energía potencial. Como consecuencia, el agua agitada por las paletas se clienta debido a la fricción.
Si el bloque de masa M desciende una altura h, la energía potencial disminuye en Mgh, y ésta es la energía que se utiliza para calentar el agua (se desprecian otras pérdidas).
Joule encontró que la disminución de energía potencial es proporcional al incremento de temperatura del agua. La constante de proporcionalidad (el calor específico de agua) es igual a 4.186 J/(g ºC). Por tanto, 4.186 J de energía mecánica aumentan la temperatura de 1g de agua en 1º C. Se define la caloría como 4.186 J sin referencia a la sustancia que se está calentando.
1 cal=4.186 J
En la simulación de la experiencia de Joule, se desprecia el equivalente en agua del calorímetro, del termómetro, del eje y de las paletas, la pérdida de energía por las paredes aislantes del recipiente del calorímetro y otras pérdidas debidas al rozamiento en las poleas, etc.
- Sea M la masa del bloque que cuelga y h su desplazamiento vertical
- m la masa de agua del calorímetro
- T0 la temperatura inicial del aguay T la temperatura final
- g=9.8 m/s2 la aceleración de la gravedad
La conversión de energía mecánica íntegramente en calor se expresa mediante la siguiente ecuación.
Mgh=mc(T-T0)
Se despeja el calor específico del agua que estará expresado en J/(kg K).
Como el calor especifico del agua es por definición c=1 cal/(g ºC), obtenemos la equivalencia entre las unidades de calor y de trabajo o energía.
Actividades
Se introduce
- La masa M del bloque que cuelga (en kg), en el control titulado Pesa que cuelga.
- La masa m de agua (en g) o su volumen en ml, en el control titulado Masa de agua.
- La temperatura inicial T0 se fijado en el programa interactivo en el valor de 20ºC
Se pulsa el botón titulado Nuevo.
Observamos la caída del bloque, que mueve unas aspas que están dentro del calorímetro. El rozamiento de las aspas en movimiento con el agua eleva su temperatura. Se deja caer el bloque una altura h y se apunta la temperatura T final del agua calentada.
Ejemplo:
Se introduce
- Masa del bloque M=50 kg
- Masa del agua en g (o volumen del agua en ml), m=100 g=0.10 kg
Se apunta
- Altura h=1 m
- Temperatura inicial T0=20ºC, y la temperatura final T=21.2ºC
Tenemos que aumentar la diferencia de temperaturas para obtener un mejor resultado. En la experiencia real se consigue haciendo caer varias veces el bloque. El trabajo total es n·Mgh, siendo n el número de veces que se suelta el bloque. En la experiencia simulada conseguimos el mismo efecto aumentando la masa M del bloque
Trabajo de la fuerza de rozamiento
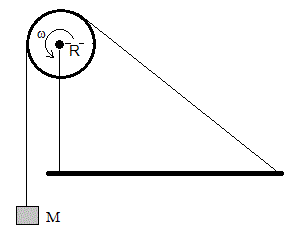
Se enrolla una cuerda varias veces alrededor de un cilindro metálico de radio R, se fija por un extremo y por el otro cuelga una masa M. Se hace girar el cilindro mediante un motor o una manivela a velocidad angular constante ω. Mientras la cuerda (una banda elástica) desliza sobre la superficie lateral del cilindro, la mayor parte del trabajo mecánico Mg·Rθ, se convierte en calor Q debido al rozamiento entre las superficies puestas en contacto.
Una parte de dicho calor se invierte en calentar el cilindro metálico, la cuerda, el termómetro situado en el eje del cilindro
C(T-T0), donde C es la capacidad calorífica total de los cuerpos
Otra parte, se disipa a la atmósfera cuya temperatura supondremos fija e igual a T0. La ley del enfriamiento de Newton nos dice que el calor perdido por un cuerpo a temperatura T en la unidad de tiempo es proporcional a la diferencia de temperaturas entre dicho cuerpo T y el ambiente T0.
En un intervalo de tiempo dt, el cilindro ha girado un ángulo dθ=ω·dt y la temperatura del cilindro metálico se ha elevado dT y además se ha perdido una energía dQ.
Integramos esta ecuación con las siguientes condiciones iniciales en el instante t=0, la temperatura inicial es la ambiente, T0
No medimos el tiempo, t ni la velocidad angular ω, sino que contamos el número de vueltas por segundo f y el número total de vueltas, N
o bien,
Conocidos los datos experimentales de N vueltas y la diferencia de temperatura T-T0, ajustamos los pares de datos a dicha función para obtener los parámetros A y B, a partir de los cuales obtenemos la constante k y la capacidad calorífica C.
Ejemplo
Sea un cilindro de aluminio de masa m=150 g y radio R=2.45 cm. Se enrolla una cuerda varias veces, alrededor del cilindro, de la que cuelga un peso de M=4 kg. Se hace girar el cilindro mediante un motor o una manivela a razon de 10 vueltas cada 18 s, f=10/18 vueltas/s. Se mide la temperatura cada 20 vueltas, hasta 400 vueltas o durante un tiempo de 720 s
Se han tomado los siguientes datos de la 'experiencia' simulada (más abajo) en un ambiente cuya temperatura es T0=25.00 °C
| N | T | N | T | |
|---|---|---|---|---|
| 20 | 25.90 | 220 | 33.65 | |
| 40 | 26.78 | 240 | 34.31 | |
| 60 | 27.63 | 260 | 34.96 | |
| 80 | 28.46 | 280 | 35.58 | |
| 100 | 29.27 | 300 | 36.19 | |
| 120 | 30.05 | 320 | 36.78 | |
| 140 | 30.81 | 340 | 37.36 | |
| 160 | 31.55 | 360 | 37.92 | |
| 180 | 32.27 | 380 | 38.46 | |
| 200 | 32.97 | 400 | 38.99 |
Se representan los datos 'experimentales' N, número de vueltas, en el eje X y la diferencia de temperaturas T-T0, en el eje Y. Se ajusta a una función que depende de dos parámetros A y B mediante
x=0:20:400;
y=[25,25.90,26.78,27.63,28.46,29.27,30.05,30.81,31.55,32.27,
32.97,33.65,34.31,34.96,35.58,36.19,36.78,37.36,37.92,38.46,38.99]-25;
hold on
plot(x,y,'ro','markersize',4,'markerfacecolor','r')
f=@(a,x) a(1)*(1-exp(-x*a(2)));
error=@(a) sum((y-f(a,x)).^2);
a0=[20 100e-5]; %valor inicial
af=fminsearch(error,a0);
text(200,1,sprintf('(%2.4f, %1.4f)',af(1),af(2)))
g=@(x) f(af,x);
fplot(g,[x(1),x(end)])
title('Ajuste no lineal')
ylabel('T-T_0')
xlabel('N')
grid on
hold off
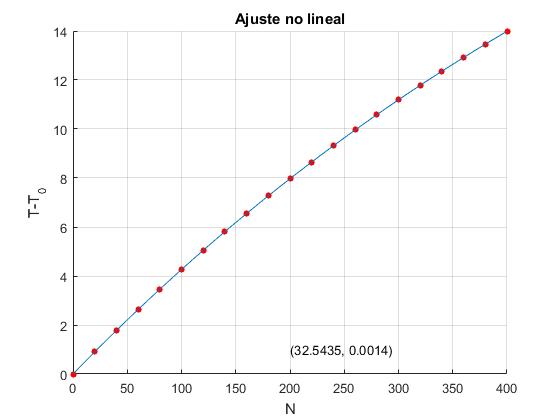
af = 32.5435 0.0014
A partir de los valores de los dos parámetros de ajuste, A=32.5435 y B=0.0014, calculamos la constante k y la capacidad calorífica C del metal
Conocida la masa del cilindro de aluminio es m=150 g (se desprecia la masa del termómetro y la cuerda), el calor específico del aluminio es c=C/m=0.88 J/(g°C).
Si conocemos el calor específico del aluminio 0.217 cal/(g°C). El factor de conversión de calorías a julios es 0.88/0.217=4.05, próximo al valor 4.186 J/cal. Este es otro posible procedimiento para determinar el equivalente mecánico del calor
Actividades
Se introduce
- Se elige el metal del que está hecho el cilindro, en el control titulado Metales
- La masa m en g del cilindro, en el control titulado Masa cilindro
- Se ha fijado el radio del cilindro en R=2.45 cm
- La masa M en kg del peso que cuelga, en el control titulado Pesa
- Se ha fijado la velocidad angular constante del motor, f=10/18 vueltas/s
- La constante k de pérdida de calor a la atmósfera se genera aletoriamente entre 0.1 y 0.3 J/(s°C)
- La temperatura inicial del cilindro y ambiente se han fijado en T0=25°C
| Metal | Calor específico cal/(g°C) |
|---|---|
| Aluminio | 0.217 |
| Cobre | 0.093 |
| Acero | 0.110 |
Se pulsa el botón titulado Nuevo
La cuerda enrollada al cilindro de metal que gira y de la que pende un peso, se muestra en color azul
En la parte derecha, se genera una tabla de datos: número de vueltas N del cilindro, temperatura del cilindro T
Referencias
José A Ibañez Mengual, Ramón P Valerdi Pérez, José A García Gamuz. Determination of heat capacities of metallic materials from the calorific balance in a friction process Eur. J. Phys. 38 (2017) 035101

