La ecuación de estado de un gas ideal es PV=nRT

P es la presión del gas, V es el volumen, T es la temperatura, n es el número de moles y R la constante de los gases
Describe aproximadamente la conducta de los gases reales a muy bajas presiones.

La ecuación de van der Waals tiene en cuenta el volumen finito de las moléculas y las fuerzas atractivas que una molécula ejerce sobre otra a distancias muy cercanas entre ellas.

${\displaystyle \left(P+\frac{n^{2}a}{V^2}\right)\left(V-nb\right)=nRT}$

Las constantes a y b son característicos de cada gas y se obtienen a partir de los datos de la presión, P_c, volumen V_c y la temperatura T_c crítica. El punto crítico es un punto de inflexión de la isoterma T_c en el diagrama P-V de modo que se cumple que

${\displaystyle \begin{array}{l}{\left(\frac{\partial P}{\partial V}\right)}_T=0\frac{-nRT}{{\left(V-nb\right)}^2}+\frac{2n^{2}a}{V^3}=0\\ {\left(\frac{{\partial }^{2}P}{\partial V^2}\right)}_T=0\frac{2nRT}{{\left(V-nb\right)}^3}-\frac{6n^{2}a}{V^4}=0\end{array}}$

De estas dos ecuaciones obtenemos, el volumen V_c y la temperatura T_c crítica.

${\displaystyle V_c=3nb{T}_c=\frac{8a}{27Rb}}$

Sustituyendo V_c y T_c en la ecuación de van der Waals obtenemos la presión crítica, P_c,

${\displaystyle P_c=\frac{a}{27b^2}}$

Escribimos la ecuación de van der Waals universal más simple en términos de nuevas variables: p=P/P_c, v=V/V_c y t=T/T_c

${\displaystyle \left(p+\frac{3}{v^2}\right)\left(3v-1\right)=8t}$

En el punto crítico p_c=1, t_c=1 y v_c=1.

Como vamos a dibujar las isotermas en un diagrama P-V, despejamos la presión p.

${\displaystyle p=\frac{8t}{3v-1}-\frac{3}{v^2}}$

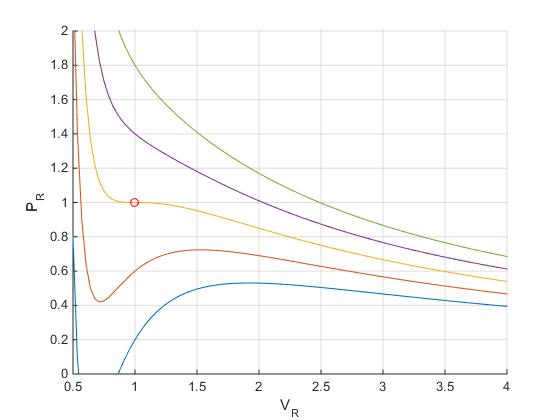
Creamos un script para representar las isotermas de temperaturas t=0.8,0.9,1.0,1.1 y 1.2. Señalamos con una marca el punto crítico tal como se aprecia en la figura

f=@(t,x) 8*t./(3*x-1)-3./(x.^2);
hold on
axis([0.5 4 0 2])
for t=0.8:0.1:1.2;
    v=linspace(0.5,4,100);
    p=f(t,v);
    plot(v,p)
end
plot(1,1,'ro')
xlabel('V_R')
ylabel('P_R')
grid on
hold off

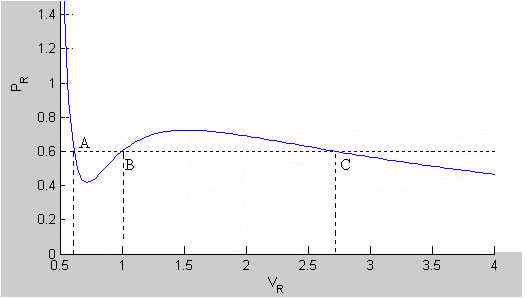
Examinamos las isotermas por debajo de la temperatura crítica t<1.

En la figura vemos que para una determinada presión p, la recta p=cte corta a la curva en tres puntos A, B y C. Los volúmenes v₁, v₂ y v₃ que corresponden a estos tres puntos se obtienen resolviendo la ecuación cúbica

${\displaystyle v^3-\frac{8t+p}{3p}{v}^2+\frac{3}{p}v-\frac{1}{p}=0}$

Para obtener las raíces, utilizamos la función roots de MATLAB o la función raices_3 que nos calcula las tres raíces exactas de una ecuación de tercer grado.

function x = raices_3(p)
    Q=(p(2)*p(2)-3*p(3))/9;
    R=(2*p(2)^3-9*p(2)*p(3)+27*p(4))/54;
    x=zeros(3,1);
    if (R*R)<(Q^3)
        tetha=acos(R/sqrt(Q^3));
        x(1)=-2*sqrt(Q)*cos(tetha/3)-p(2)/3;
        x(2)=-2*sqrt(Q)*cos((tetha+2*pi)/3)-p(2)/3;
        x(3)=-2*sqrt(Q)*cos((tetha-2*pi)/3)-p(2)/3;
    else
        A=-sign(R)*nthroot(abs(R)+sqrt(R*R-Q^3),3);
        if A==0
            B=0;
        else
            B=Q/A;
        end
        x(1)=(A+B)-p(2)/3;
        x(2)=-(A+B)/2-p(2)/3+(sqrt(3)*(A-B)/2)*sqrt(-1); 
        x(3)=-(A+B)/2-p(2)/3-(sqrt(3)*(A-B)/2)*sqrt(-1);
    end
end

Ordenamos los valores de las raíces de menor a mayor mediante la función sort de MATLAB.

La isoterma de temperatura t, tiene un mínimo y un máximo local. Determinamos sus coordenadas (v_m1, p_m1) y (v_m2, p_m2) calculando la derivada primera e igualando a cero.

${\displaystyle \begin{array}{l}p=\frac{8t}{3v-1}-\frac{3}{v^2}\\ {\left(\frac{\partial p}{\partial v}\right)}_t=0-\frac{24t}{{\left(3v-1\right)}^2}-\frac{6}{v^3}=0\\ v^3-\frac{9}{4t}{v}^2+\frac{3}{2t}v-\frac{1}{4t}=0\end{array}}$

Tenemos de nuevo, que calcular las raíces de una ecuación cúbica.

En la zona de transición entre la fase gaseosa y la fase líquida la presión no oscila, se mantiene constante y el potencial químico se mantiene constante. La regla de Maxwell elimina el comportamiento oscilante de la isoterma de la ecuación de van der Waals y la sustituye por un segmento horizontal de presión p_r tal que el área comprendida entre el segmento horizontal AB y la isoterma es igual al área comprendida entre la isoterma y el segmento horizontal BC, tal como se ve en la figura más abajo.

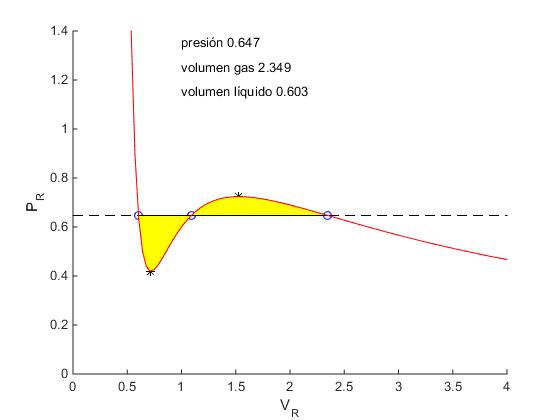
En la figura, vemos la isoterma de temperatura t=0.9,

• los extremos locales identificados con el símbolo '*',
• la presión p_r para la cual las áreas sombreadas de color amarillo son iguales.
• los puntos de corte de la isoterma con la recta p_r =cte

El el área A₁comprendida entre el segmento horizontal AB y la isoterma se calcula integrando

${\displaystyle \begin{array}{l}p\left(v_2-v_1\right)-{\displaystyle \underset{v_1}{\overset{v_2}{\int }}p·dv=}\\ p\left(v_2-v_1\right)-{\displaystyle \underset{v_1}{\overset{v_2}{\int }}\left(\frac{8t}{3v-1}-\frac{3}{v^2}\right)·dv=}\\ p\left(v_2-v_1\right)-\frac{8}{3}t\ln \frac{3v_2-1}{3v_1-1}-3\left(\frac{1}{v_2}-\frac{1}{v_1}\right)\end{array}}$

El el área A₂ comprendida entre el segmento horizontal BC y la isoterma se calcula integrando

${\displaystyle \begin{array}{l}{\displaystyle \underset{v_2}{\overset{v_3}{\int }}p·dv-p\left(v_3-v_2\right)=}\\ \frac{8}{3}t\ln \frac{3v_3-1}{3v_2-1}+3\left(\frac{1}{v_3}-\frac{1}{v_2}\right)-p\left(v_3-v_2\right)\end{array}}$

Creamos una función denominada igualArea que calcule la diferencia entre las dos áreas A₁-A₂.

function res=igualArea(p,t)
    pol=[1 -(p+8*t)/(3*p) 3/p -1/p];
    v = sort(raices_3(pol));
    area_1 = p*(v(2)-v(1))-8/3*t*log((3*v(2)-1)
/(3*v(1)-1))-3*(v(1)-v(2))/(v(1)*v(2));
    area_2 =8/3*t*log((3*v(3)-1)/(3*v(2)-1))+3*(v(2)-v(3))
/(v(2)*v(3))-p*(v(3)-v(2));
    res=area_1-area_2;
end

Creamos un script para realizar las siguientes tareas:.

1. Establezca el valor de la temperatura t reducida, menor que la unidad

2. Represente la isoterma de color rojo en el diagrama P-V.

3. Calcule el mínimo p_m1 y máximo p_m2 local resolviendo la ecuación de tercer grado en v.

4. La presión p_r buscada estará en el intervalo (p_m1, p_m2), o bien en el intervalo (0, p_m2) si p_m1 fuese negativa (la presión es siempre positiva). El manejador (handle) de esta función igualArea se lo pasaremos a la función fzero de MATLAB para que calcule el valor p_r de la presión que hace la que diferencia de áreas sea nula.

5. Una vez obtenido el valor de la presión p_r, se calcula las raíces de la ecuación cúbica para determinar los volúmenes v₁, v₂ y v₃. El primero corresponde al volumen de la fase líquida y el tercero al del gas, para la presión p_r y la temperatura t

6. Rellene de color amarillo las dos regiones, para mostrar visualmente que las áreas son iguales.

t=input('temperatura reducida (0.8-1): ');
%gráfica de la isoterma
f=@(x) 8*t./(3*x-1)-3./(x.^2);
Vr=linspace(0.5,4,100);
Pr=f(Vr);
hold on
axis([0 4 0 1.4])
plot(Vr,Pr,'r')
xlabel('V_R')
ylabel('P_R')

%máximo y mínimo
pol=[1 -9/(4*t) 3/(2*t) -1/(4*t)];
z=sort(raices_3(pol));
plot(z(1),f(z()),z(2),f(z(2)),'k*',z(3),f(z(3)),'k*')
if f(z(2))>0
    a=f(z(2))+0.01;
else
    a=0.01;
end
b=f(z(3))-0.01;
%calcula p para que las áreas sean iguales
f1=@(p)igualArea(p,t);
p=fzero(f1,[a b]);
%igualArea(p,t) %para comprobar que las areas son iguales
plot([0 4],[p p],'k--') 
pol=[1 -(p+8*t)/(3*p) 3/p -1/p];
v = sort(raices_3(pol));
plot(v(1),p,'bo',v(2),p,'bo',v(3),p,'bo')

%rellenar la areas
xx = [v(1) Vr(Vr >= v(1) & Vr <= v(2))  v(2)];
yy = [f(v(1)) Pr(Vr >= v(1) & Vr <= v(2)) f(v(2))];
fill(xx,yy,'y')

xx = [v(2) Vr(Vr >= v(2) & Vr <= v(3)) v(3)];
yy = [f(v(2)) Pr(Vr >= v(2) & Vr <= v(3)) f(v(3))];
fill(xx,yy,'y')
plot(Vr,Pr,'r')
%imprimir datos
text(1,1.35,sprintf('presión %1.3f',p))
text(1,1.25,sprintf('volumen gas %1.3f',v(3)))
text(1,1.15,sprintf('volumen líquido %1.3f',v(1)))

hold off

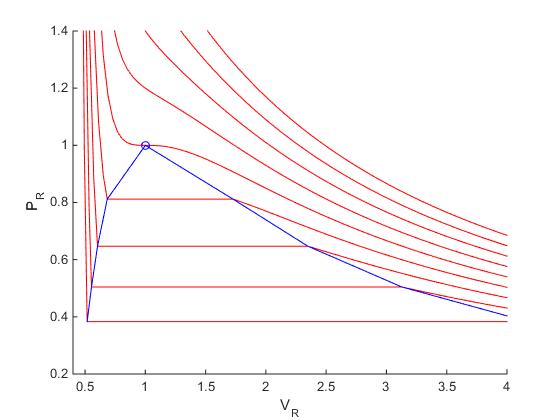
Ahora vamos a dibujar varias isotermas por encima y por debajo del punto crítico t=1. Sustituiremos la región ondulada entre v_liquido y v_gas a la presión p_r por un segmento y uniremos los puntos que marcan la región de coexistencia de las dos fases, tal como se muestra en la figura.

Creamos un script para que realice las siguientes tareas.

1. Dibuje las isotermas t≥1 (para t=1,1.05,1.1,1.15 y 1.2)

2. Dibuje las isotermas para t<1 (para t=0.8, 0.85, 0.9, 0.95).

• Para cada isoterma se calcula el volumen v_liquido=v(1) y v_gas=v(3) a la presión p_r resolviendo la ecuación trascedente A₁-A₂=0, mediante la función fzero, guardando los datos en una matriz bidimiensional (volumen, presión).

• Se sustituye la región ondulada por el segmento que une v(1) y v(3) a la presión p_r

3. Se añade a la matriz bidimensional las coordendas del punto crítico v=1 y p=1. Ordenamos la matriz de datos (v,p) utilizando la función MATLAB sortrows, y unimos los puntos (v,p) mediante líneas de color azul tal como se muestra en la figura.

Vr=linspace(0.1,4,100);
hold on
i=1;
PV=zeros(9,2);
axis([0.4 4 0.2 1.4])
for t=0.8:0.05:1.2;
    f=@(x) 8*t./(3*x-1)-3./(x.^2);
    if t<1
        %calcula máximo y mínimo local de p
        pol=[1 -9/(4*t) 3/(2*t) -1/(4*t)];
        z=sort(raices_3(pol));
        if f(z(2))>0
            a=f(z(2))+0.01;
        else
            a=0.01;
        end
        b=f(z(3))-0.01;
        %calcula p para que las áreas sean iguales
        f1=@(p)igualArea(p,t);
        p=fzero(f1,[a b]);
        pol=[1 -(p+8*t)/(3*p) 3/p -1/p];
        v = sort(raices_3(pol));
        %guarda Vlíquido, Vgas y la presión constante p 
        PV(i,1)=v(1);PV(i,2)=p;
       PV(i+1,1)=v(3);PV(i+1,2)=p;
       i=i+2;
 %gráfica
        Pr=f(Vr);
        Vf = [Vr(Vr <= v(1)) v(1) v(3) Vr(Vr>= v(3))];
        Pf = [Pr(Vr <= v(1)) f(v(1)) f(v(3)) Pr(Vr>= v(3))];
        plot(Vf,Pf,'r')
    else %en el punto crítico y por encima
        Pr=f(Vr);
        plot(Vr,Pr,'r')
    end 
end
%une los puntos (p Vlíquido), (p Vgas) cambio de fase
PV(i,1)=1; PV(i,2)=1; %punto crítico
PVs=sortrows(PV,1);
plot(PVs(:,1),PVs(:,2),'b')
plot(1,1,'bo') %punto crítico
xlabel('V_R')
ylabel('P_R')
hold off