Extracción óptima del calor
Cuando una masa m1 de agua a temperatura T1 se pone en contacto con una masa m2 a la temperatura T2, la temperatura de equilibrio Te es
donde c es el calor específico del agua supuesto constante (que no cambia con la temperatura)
N=1
Se supone que los dos recipientes contienen una masa m del mismo líquido, tienen masa despreciable y conducen perfectamente el calor. No hay pérdidas debidas a la radiación, evaporación o conducción del calor a los alrededores.
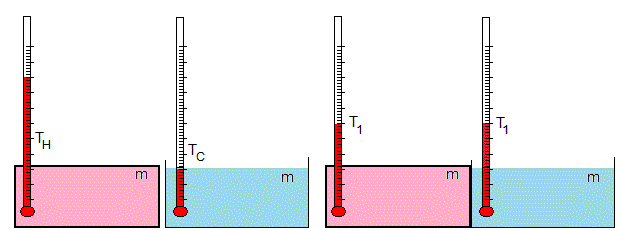
Si los recipientes contienen la misma masa m de líquido, la temperatura de equilibrio es
Sea TH=80 °C y TC=20 °C, la temperatura final es T1=50 °C
N=2, porciones
Supongamos que el recipiente abierto se divide en dos recipientes de masa m/2 a la misma temperatura TC
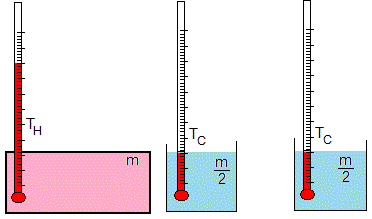
Se pone en contacto el recipiente cerrado de masa m a la temperatura TH con el recipiente abierto de masa m/2 a la temperatura TC. La temperatura T1 de equilibrio es
Se pone en contacto el recipiente cerrado de masa m a la temperatura T1 con el recipiente abierto de masa m/2 a la temperatura TC. La temperatura final T2 es
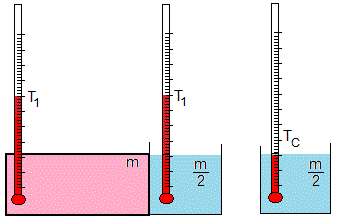
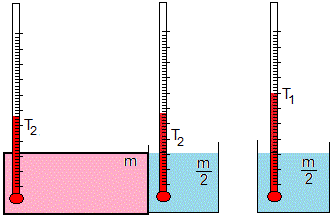
Sea TH=80 °C y TC=20 °C. Las temperaturas T1=60 °C y T2=46.7 °C. La temperatura final del recipiente cerrado es más baja.
Comprobación
La conservación de la energía exige que
Introduciendo las expresiones de T1 y T2
Las dos porciones de masa m/2 cada una, están a temperaturas T1 y T2. Si se juntan en un recipiente, la temperatura Tm de la mezcla es
Los dos porciones de distinto tamaño
Supongamos que las masas de los recipientes abiertos son distintas, una es m1 y otra es m2 a la temperatura inicial TC, tal que m1+m2=m
Se pone en contacto el recipiente cerrado de masa m a la temperatura TH con el recipiente abierto de masa m1 a la temperatura TC. La temperatura T1 de equilibrio es
Se pone en contacto el recipiente cerrado de masa m a la temperatura T1 con el recipiente abierto de masa m2 a la temperatura TC. La temperatura T2 de equilibrio es
Sea TH=80 °C y TC=20 °C. Representamos la temperatura final T2 en función de x.
TH=80;
TC=20;
f=@(x) (TH+(1+x-x.^2)*TC)./((2-x).*(1+x));
fplot(f,[0,1])
grid on
xlabel('x')
ylabel('T')
title('Temperatura final')
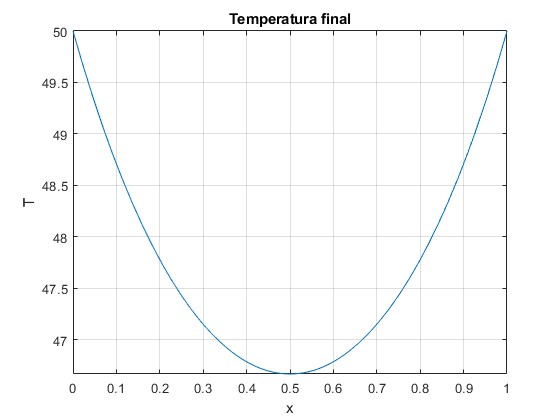
El mínimo de T2 se produce para x=1/2, cuando los dos recipientes abiertos tienen la misma masa. El valor del mínimo es
>> f(0.5) ans = 46.6667
En una determinada escala de temperaturas, TC=0. Determinamos el mínimo de T2 o de la función
N=3, porciones
Supongamos que el recipiente abierto se divide en tres recipientes de masa m/3 a la misma temperatura TC
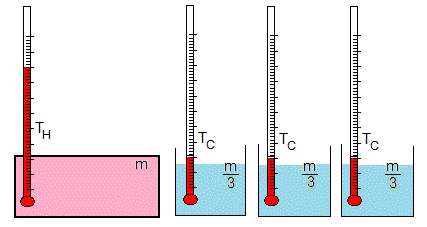
Se pone en contacto el recipiente cerrado de masa m a la temperatura TH con el recipiente abierto de masa m/3 a la temperatura TC. La temperatura T1 de equilibrio es
Se pone en contacto el recipiente cerrado de masa m a la temperatura T1 con el recipiente abierto de masa m/3 a la temperatura TC. La temperatura T2 de equilibrio es
Se pone en contacto el recipiente cerrado de masa m a la temperatura T2 con el recipiente abierto de masa m/3 a la temperatura TC. La temperatura final T3 es
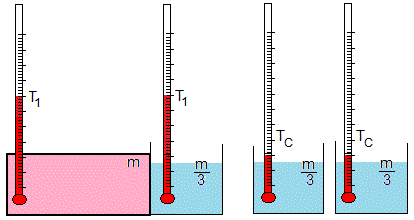
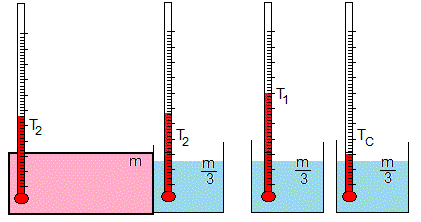
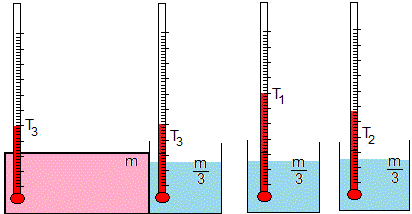
Sea TH=80 °C y TC=20 °C. Las temperaturas T1=65 °C, T2=53.75 °C y T3=45.3 °C. La temperatura final del recipiente cerrado es algo más baja.
Comprobación
La conservación de la energía exige que
Las tres porciones de masa m/3 cada una, están a temperaturas T1, T2 y T3. Si se juntan en un recipiente, la temperatura Tm de la mezcla es
Los tres porciones de distinto tamaño
Supongamos que las masas de los recipientes abiertos son distintas, una es m1, otra es m2 y la tercera m3 a la temperatura inicial TC, tal que m1+m2+m3=m
Se pone en contacto el recipiente cerrado de masa m a la temperatura TH con el recipiente abierto de masa m1 a la temperatura TC. La temperatura T1 de equilibrio es
Se pone en contacto el recipiente cerrado de masa m a la temperatura T1 con el recipiente abierto de masa m2 a la temperatura TC. La temperatura T2 de equilibrio es
Se pone en contacto el recipiente cerrado de masa m a la temperatura T2 con el recipiente abierto de masa m3 a la temperatura TC. La temperatura final T3 es
Sea TH=80 °C y TC=20 °C. Representamos T3 en función de x e y.
TH=80;
TC=20;
f=@(x,y) (TH+TC*(x+y+x.*y+(1-x-y).*(1+x).*(1+y)))./((1+y).*(1+x).*(2-x-y));
[x,y]=meshgrid(0:0.01:0.5,0:0.01:0.5);
z=f(x,y);
hold on
mesh(x,y,z);
plot3(1/3,1/3,f(1/3,1/3),'ro','markersize',3,'markerfacecolor','r')
hold off
grid on
xlabel('x')
ylabel('y')
zlabel('T')
title('Temperatura final')
view(-34,46)
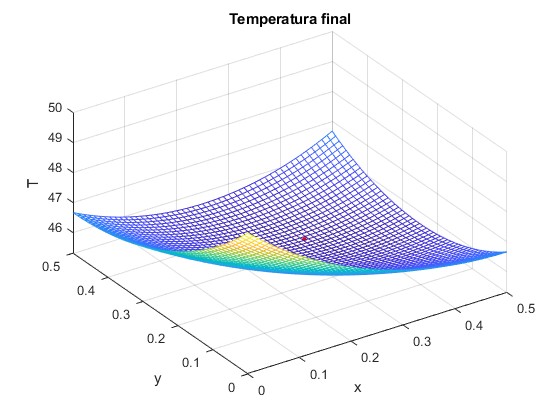
El mínimo de T3 se produce para x=1/3, cuando los tres recipientes abiertos tienen la misma masa. El valor del mínimo es
>> f(1/3,1/3) ans = 45.3
En una determinada escala de temperaturas, TC=0. Determinamos el mínimo de T3 o de la función de dos variables
Las porciones han de ser iguales a m/3 para que T3 sea mínima
N porciones del mismo tamaño
Supongamos que el recipiente abierto se divide en N recipientes de masa m/N a la misma temperatura TC
Se pone en contacto el recipiente cerrado de masa m a la temperatura TH con el recipiente abierto de masa m/N a la temperatura TC. La temperatura T1 de equilibrio es
Se pone en contacto el recipiente cerrado de masa m a la temperatura T1 con el recipiente abierto de masa m/N a la temperatura TC. La temperatura T2 de equilibrio es
Se pone en contacto el recipiente cerrado de masa m a la temperatura T2 con el recipiente abierto de masa m/N a la temperatura TC. La temperatura T3 de equilibrio es
Se pone en contacto el recipiente cerrado de masa m a la temperatura Ti con el recipiente abierto de masa m/N a la temperatura TC. La temperatura Ti+1 de equilibrio es
Se pone en contacto el recipiente cerrado de masa m a la temperatura TN-1 con el recipiente abierto de masa m/N a la temperatura TC. La temperatura final TN de equilibrio es
Multiplicando a TC/(N+1) tenemos la suma de N términos de una progresión geométrica cuyo primer término es 1, la razón es N/(N+1)
>> syms k N; >> symsum((N/(N+1))^k,0, N-1) ans =N - (N^N*(N + 1))/(N + 1)^N + 1
La temperatura final TN del recipiente cerrado será
Comprobación. Temperaturas finales
Las N porciones de masa m/N cada una, están a temperaturas T1, T2,... TN. Si se juntan en un recipiente, la temperatura Tm de la mezcla es
Las N porciones de distinto tamaño
Para que TN sea mínima, las porciones han de ser iguales a m/N. Para demostrarlo, hay que minimizar una función de N-1 variables
Tenemos que resolver un sistema de N-1 ecuaciones con N-1 incógnitas cuya solución es xi=1/N (i=1,2,3...N-1). Por ejemplo, para N=4
es la solución del sistema de tres ecuaciones con tres incógnitas
Infinitas porciones del mismo tamaño
Calculamos la temperatura final T∞ cuando N→∞
La definición de número e es
>> syms n; >> limit((1+1/n)^n,n,inf) ans =exp(1)
La temperatura final es
Sea TH=80 °C y TC=20 °C. Representamos la temperatura final TN en función de N=1, 2, 3, 4.... ∞
TH=80;
TC=20;
f=@(N) TC+(TH-TC)*(N./(N+1)).^N;
nn=1:50;
plot(nn,f(nn),'ro','markersize',3,'markerfacecolor','r')
T_inf=TC+(TH-TC)/exp(1);
line([0,50],[T_inf, T_inf])
grid on
xlabel('N')
ylabel('T')
title('Temperatura final')
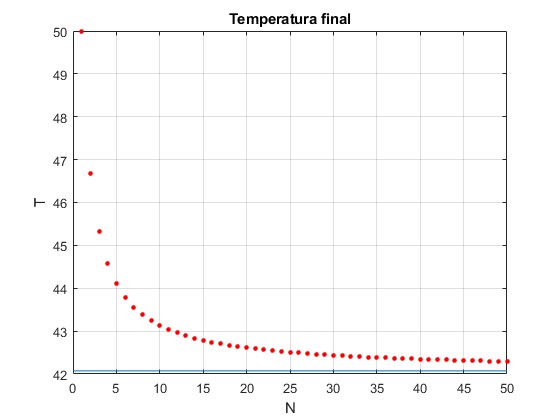
La temperatura final mínima T∞=42.07 °C, es la asíntota horizontal (recta de color azul)
Se divide el recipiente inicialmente caliente en el mismo número de porciones
Vamos a dividir el recipiente inicialmente caliente en el mismo número de porciones iguales y las vamos a poner en contacto con las porciones frías. Como dos trenes iguales que se mueven en vías paralelas pero en sentido contrario. Los vagones representan las porciones de líquido que cuando coinciden entran en contacto intercambiado calor hasta alcanzar el equilibrio térmico a la misma temperatura.
Supondremos que el recipiente caliente de masa m está al temperatura TH=1. El recipiente frío de la misma masa está a la temperatura TC=0
N=2, porciones iguales
Dividimos el recipiente caliente y el frío en dos porciones de masa m/2
Las porciones de agua caliente se identifican mediante el índice j, se mueven de derecha a izquierda. Las porciones de agua fría se identifican con el índice i, se mueven de izquierda a derecha.
Estado inicial. Entran en contacto las porciones i=1, j=1
Entran en contacto las porciones i=1, j=2, e i=2, j=1
Entran en contacto las porciones i=2, j=2
Estado final

La temperatura de equilibrio es T1,1=1/2
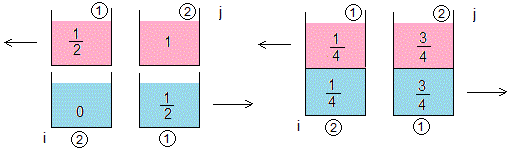
Las temperaturas de equilibrio son T2,1=1/4, T1,2=3/4
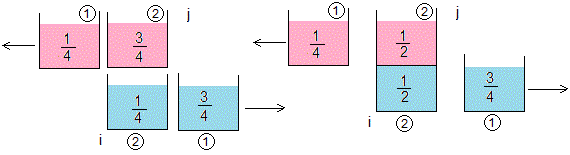
La temperatura de equilibrio es T2,2=1/2
Las temperaturas finales de las cuatro porciones son
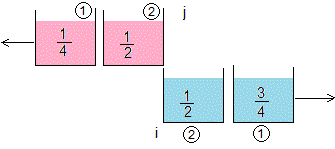
La temperatura media de las dos porciones de agua caliente es Tcaliente=(1/4+1/2)/2=0.375
La temperatura media de las dos porciones de agua fría es Tfría=(1/2+3/4)/2=0.625
N=3, porciones iguales
Dividimos el recipiente caliente y el frío en tres porciones de masa m/3
Estado inicial. Entran en contacto las porciones i=1, j=1
Entran en contacto las porciones i=1, j=2, e i=2, j=1
Entran en contacto las porciones i=3, j=1; i=2, j=2 e i=1, j=3
Entran en contacto las porciones i=3, j=2; i=2, j=3
Entran en contacto las porciones i=3, j=3
Estado final
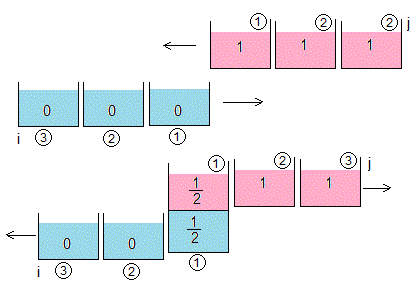
La temperatura de equilibrio es T1,1=1/2
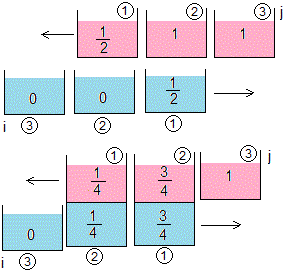
Las temperaturas de equilibrio son T2,1=1/4, T1,2=3/4
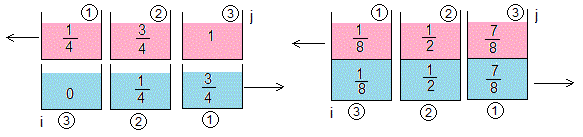
Las temperaturas de equilibrio son T3,1=1/8, T2,2=1/2 y T1,3=7/8
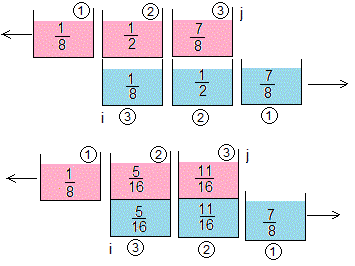
Las temperaturas de equilibrio son T3,2=5/16 y T2,3=11/16
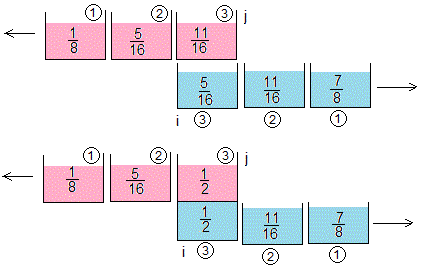
La temperatura de equilibrio es T3,3=1/2
Las temperaturas finales de las seis porciones son
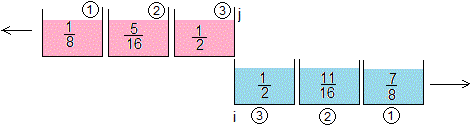
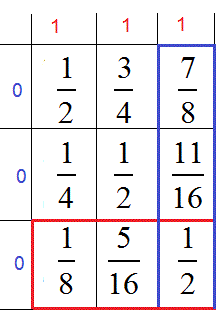
Expresamos las temperaturas mediante una matriz
La primera columna Ti,0=0, corresponde a la temperatura inicial de las porciones del recipiente frío. La última columna, Ti, N (i=1,2,3) corresponde a sus temperaturas finales. La temperatura media final <Tfría>=(7/8+11/16+1/2)/3=0.6875 (algo más alta que para N=2). En general
La primera fila T0,j=0, corresponde a la temperatura inicial de las porciones del recipiente caliente. La última fila, TN, j (j=1,2,3) corresponde a sus temperaturas finales. La temperatura media final <Tcaliente>=(1/8+5/16+1/2)/3=0.3125 (algo más baja que para N=2). En general
Los elementos de la matriz se generan mediante un proceso iterativo
Los elementos de la matriz tienen las siguientes propiedades
N=3;
T=zeros(N+1,N+1);
T(1,2:N+1)=1;
T(2:N+1,1)=0;
format rat
for i=2:N+1
for j=2:N+1
T(i,j)=(T(i-1,j)+T(i,j-1))/2;
end
end
disp(T)
%medias
format short
T_c=sum(T(N+1,2:N+1))/N;
T_f=sum(T(2:N+1,N+1))/N;
fprintf('Media fría %1.3f, Media caliente %1.3f\n', T_f, T_c)
0 1 1 1
0 1/2 3/4 7/8
0 1/4 1/2 11/16
0 1/8 5/16 1/2
Media fría 0.688, Media caliente 0.312
N=6 porciones iguales
Dividimos el recipiente caliente y el frío en seis porciones de masa m/6
N=6;
T=zeros(N+1,N+1);
T(1,2:N+1)=1;
T(2:N+1,1)=0;
format rat %para operar con fracciones
for i=2:N+1
for j=2:N+1
T(i,j)=(T(i-1,j)+T(i,j-1))/2;
end
end
disp(T)
%medias
format short %por defecto
T_c=sum(T(N+1,2:N+1))/N;
T_f=sum(T(2:N+1,N+1))/N;
fprintf('Media fría %1.3f, Media caliente %1.3f\n', T_f, T_c)
hold on
plot(1:N, T(N+1,2:N+1),'-ro','markersize',3,'markerfacecolor','r')
plot(1:N, T(2:N+1, N+1),'-bo','markersize',3,'markerfacecolor','b')
line([0,N],[T_c,T_c],'color','r','lineStyle','--')
line([0,N],[T_f,T_f],'color','b','lineStyle','--')
hold off
grid on
xlabel('i,j')
ylabel('T')
title('Temperaturas finales')
0 1 1 1 1 1 1 0 1/2 3/4 7/8 15/16 31/32 63/64 0 1/4 1/2 11/16 13/16 57/64 15/16 0 1/8 5/16 1/2 21/32 99/128 219/256 0 1/16 3/16 11/32 1/2 163/256 191/256 0 1/32 7/64 29/128 93/256 1/2 319/512 0 1/64 1/16 37/256 65/256 193/512 1/2 Media fría 0.774, Media caliente 0.226
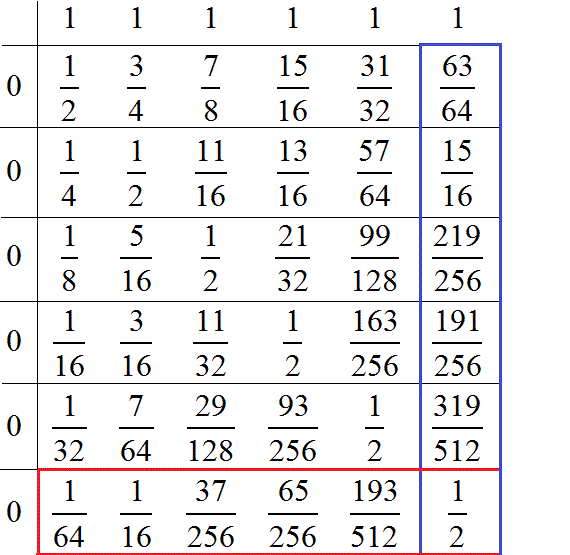
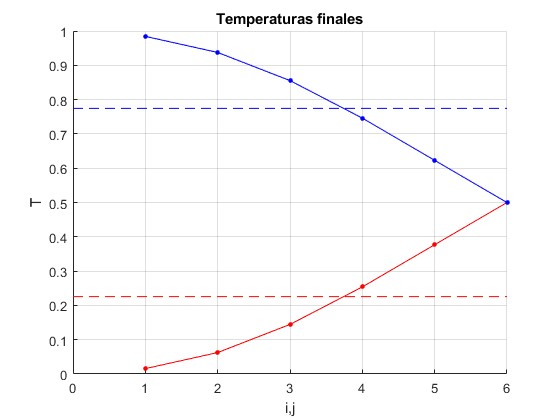
Representamos gráficamente las temperaturas finales de las porciones de líquido caliente (en rojo) y del líquido frío (en azul)
Temperaturas medias
Representamos las temperaturas medias <Tfría> y <Tcliente> en función del número de porciones N
function termico_2
nn=2:50;
tc=zeros(1,length(nn));
tf=zeros(1,length(nn));
k=1;
for n=nn
[Tc,Tf]=matriz(n);
tc(k)=Tc;
tf(k)=Tf;
k=k+1;
end
hold on
plot([1,nn], [1,tc],'-ro','markersize',3,'markerfacecolor','r')
plot([1,nn], [0,tf],'-bo','markersize',3,'markerfacecolor','b')
hold off
grid on
xlabel('N')
ylabel('T')
title('Temperaturas medias')
function [T_c,T_f]=matriz(N)
T=zeros(N+1,N+1);
T(1,2:N+1)=1;
T(2:N+1,1)=0;
format rat
for i=2:N+1
for j=2:N+1
T(i,j)=(T(i-1,j)+T(i,j-1))/2;
end
end
%medias
T_c=sum(T(N+1,2:N+1))/N;
T_f=sum(T(2:N+1,N+1))/N;
end
end
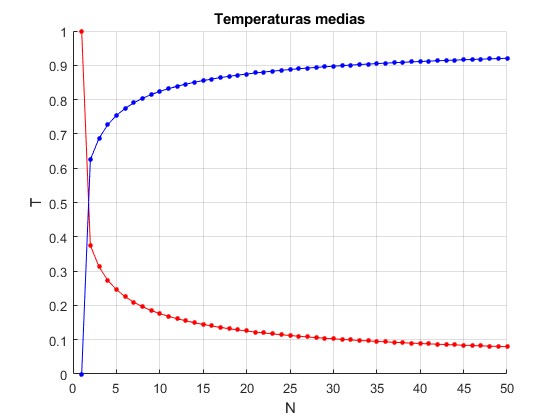
Las temperatura media del agua caliente tiende a cero en el límite cuando N→∞, pero lo hace muy lentamente. En el estado final cuando N→∞, vemos que las temperaturas del líquido inicialmente caliente se intercambia con la temperatura del líquido inicialmente frío
Referencias
Jayanth Vyasanakere P, Rajaram Nityananda Optimal Extraction of Heat: An Instructive Problem. Resonance – Journal of Science Education. Volume 27, February 2022, pp. 273-282
Eugene G. Mishchenko, Paul F. Pshenichka. Reversible temperature exchange upon thermal contact. Am. J. Phys. 85 (1), January 2017, pp. 23-29

