Descripción cualitativa

En este apartado obtendremos, mediante un razonamiento cualitativo, una expresión para la energía transportada por un movimiento ondulatorio armónico. Las líneas de razonamiento son las siguientes:

1. Examinaremos primero el concepto de flujo, para ello pensemos en el símil del agua que fluye por una cañería de sección S, con velocidad constante v. El volumen de agua que recogemos en el extremo de la cañería en la unidad de tiempo (por segundo) es igual al producto de la sección de la cañería por la velocidad de la corriente de agua.



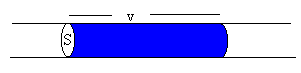
Como vemos en la figura, en la unidad de tiempo, el agua recogida es la contenida en el volumen cilíndrico de color azul, cuya sección es S y cuya longitud es v.

Flujo (volumen de agua recogida en la unidad de tiempo)=Sv

En un movimiento ondulatorio, la energía fluye desde la fuente de ondas a través del medio con la velocidad de propagación v.

2. Las partículas del medio describen movimientos armónicos simples (MAS) de amplitud Ψ₀ y frecuencia angular ω , cuando en dicho medio se propaga el movimiento ondulatorio armónico.

   Ψ(x,t)=Ψ₀·sin k(x-vt)=Ψ₀·sin (kx-ω t)

La energía de una partícula vale

${\displaystyle E_i=\frac{1}{2}{m}_i{\omega }^2\Psi {}_0^2}$

donde m_i, es la masa de la partícula, ω es la frecuencia angular del MAS y Ψ₀ es su amplitud.

3. El flujo de energía, es la energía transportada en la unidad de tiempo, será igual a la energía de todas las partículas contenidas en el volumen cilíndrico de sección S y longitud v

${\displaystyle \frac{\partial W}{\partial t}={\displaystyle \sum \frac{1}{2}}{m}_i{\omega }^2{\Psi }_0^2=\frac{1}{2}\left({\displaystyle \sum m_i}\right){\omega }^2{\Psi }_0^2=\frac{1}{2}\left(\rho Sv\right){\omega }^2{\Psi }_0^2}$

La masa de todas las partículas, entre paréntesis en la segunda igualdad, es igual al producto de la densidad ρ por el volumen del cilindro Sv.

Descripción cuantitativa

Consideremos de nuevo, el caso de las ondas elásticas longitudinales que se propagan a lo largo de una barra. Una porción de la barra de anchura dx se desplaza con velocidad $\partial \Psi /\partial t$. El lado izquierdo de la barra ejerce una fuerza (–F) sobre dicha porción.

La potencia (energía por unidad de tiempo) que el lado izquierdo trasmite al lado derecho es

${\displaystyle \frac{\partial W}{\partial t}=(-F)\frac{\partial \Psi }{\partial t}=-YS\frac{\partial \Psi }{\partial x}\frac{\partial \Psi }{\partial t}}$

Supongamos que la fuente de ondas situado en el extremo izquierdo de la barra produce un movimiento ondulatorio armónico de amplitud Ψ₀ y frecuencia ω=2πf, que se propaga hacia la derecha con velocidad v.

${\displaystyle \begin{array}{l}\Psi (x,t)={\Psi }_0\sin \left(k(x-vt)\right)={\Psi }_0\sin (kx-\omega t)\\ \frac{\partial W}{\partial t}=YS{\Psi }_0^{2}k\omega {\cos }^2(kx-\omega t)\end{array}}$

Sabiendo que la velocidad de propagación de las ondas longitudinales en la barra elástica es

${\displaystyle \begin{array}{l}v=\sqrt{\frac{Y}{\rho }}\\ \frac{\partial W}{\partial t}=YAS{\Psi }_0^{2}k\omega {\cos }^2(kx-\omega t)=S\rho v^{2}k\omega {\Psi }_0^2{\cos }^2(kx-\omega t)=S\rho v{\omega }^2{\Psi }_0^2{\cos }^2(kx-\omega t)\end{array}}$

Calculamos el valor medio

${\displaystyle \langle \frac{\partial W}{\partial t}\rangle =S\rho v{\omega }^2{\Psi }_0^2\langle {\cos }^2(kx-\omega t)\rangle =Sv\left(\frac{1}{2}\rho {\omega }^2{\Psi }_0^2\right)}$

y llegamos al mismo resultado que en la descripción cualitativa

El valor medio de la función periódica f(t) de periodo P es

${\displaystyle \begin{array}{l}<f(t)>=\frac{1}{P}{\displaystyle {\int }_0^{P}f(t)·dt}\\ <{\cos }^{2}x>=\frac{1}{\pi }{\displaystyle {\int }_0^{\pi }{\cos }^{2}x·dx=}\frac{1}{\pi }{\displaystyle {\int }_0^{\pi }\frac{1+\cos (2x)}{2}·dx=\frac{1}{2}}\end{array}}$

>> syms x;
>> int('cos(x)^2',x,0,pi)/pi
ans =1/2

Intensidad

Se define intensidad del movimiento ondulatorio, como la energía transportada por unidad de área y por unidad de tiempo. Dividiendo la fórmula anterior por el área S obtenemos una expresión general para la intensidad de un movimiento ondulatorio armónico de frecuencia angular ω y de amplitud Ψ₀ que se propaga en un medio de densidad ρ con velocidad v.

${\displaystyle I=v\left(\frac{1}{2}\rho {\omega }^2{\Psi }_0^2\right)}$

La unidad de medida es W/m², aunque para el sonido se suele emplear una medida más familiar, el decibel. El nivel de intensidad de un sonido se expresa en decibeles (abreviado db), según la definición

${\displaystyle B=10\log \frac{I}{I_0}}$

Donde I₀ es una intensidad de referencia. Para el caso del sonido en el aire el nivel de referencia tomado arbitrariamente es de 10^-12 W/m².

La ley inversa del cuadrado de la distancia.

La intensidad de un movimiento ondulatorio varía con la inversa del cuadrado de la distancia a una fuente puntual. La fuente de luz emite energía a razón de P watios (julios/segundo). Si la luz se propaga en todas las direcciones de forma isótropa, a una distancia r de la fuente, el flujo de energía atraviesa una superficie esférica de radio r.

${\displaystyle I=\frac{P}{4\pi r^2}}$

La intensidad se mide en W/m². La intensidad de la luz disminuye en razón inversamente proporcional al cuadrado de la distancia x desde la fuente al detector.

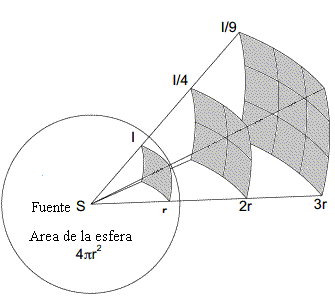
Se puede considerar al Sol como una fuente puntual de luz. La Tierra está a una distancia del Sol de una Unidad Astronómica (UA), 149,600,000 km. La intensidad de la radiación solar medida en la órbita de la Tierra  es I=1390 W/m² denominada constante solar. Júpiter que dista 5.203 UA del Sol recibirá una intensidad de

${\displaystyle I=\frac{1390}{{5.203}^2}=51.35{\text{W/m}}^{\text{2}}}$

En la experiencia de laboratorio, colocamos un sensor (light sensor de PASCO), a la izquierda en la fotografía, a una distancia x de la fuente de luz, a la derecha, que vamos cambiando. Obtenemos la siguiente tabla:

A partir de la expresión de la intensidad I en función de la distancia r a la fuente, tomamos logaritmos neperianos y obtenemos la ecuación de una recta de pendiente -2.

${\displaystyle \begin{array}{l}I=\frac{P}{4\pi r^2}\\ \ln I=a-2\ln r\end{array}}$

x=[0.20,0.25,0.30,0.35,0.40,0.45,0.50];
y=[171,106,73,52,39,30.5,24.5];
plot(log(x),log(y),'bo','markersize',2,'markerfacecolor','b')
grid on
xlabel('log(x)')
ylabel('log(y)')
title('Inversa del cuadrado de la distancia')

Corremos el script y aparece la ventana gráfica con la representación de los datos como puntos de color azul. En el menú seleccionamos Tools/Basic Fitting, aparece un cuadro de diálogo donde marcamos la casilla linear en Plot fits. A continuación, pulsamos la flecha hacia la derecha --> para mostrar los coeficientes p₁ y p₂ del polinomio (recta) y=p₁·x+p₂ de ajuste. El coeficente p₁=-2.1242 y p₂=1.732. El dato que nos interesa es la pendiente de la recta p₁ que es un valor próximo a 2.

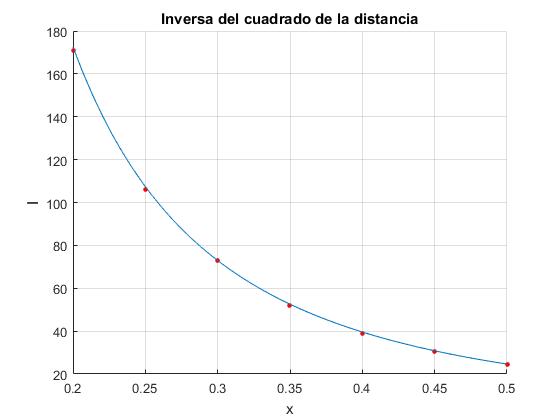
Dibujamos los datos experimentales, y la función que mejor ajusta

x=[0.20,0.25,0.30,0.35,0.40,0.45,0.50];
y=[171,106,73,52,39,30.5,24.5];
hold on
plot(x,y,'ro','markersize',3,'markerfacecolor','r')
fplot(@(x) exp(1.732)./x.^2.1242,[x(1),x(end)])
hold off
grid on
xlabel('x')
ylabel('I')
title('Inversa del cuadrado de la distancia')

El problema de la iluminación

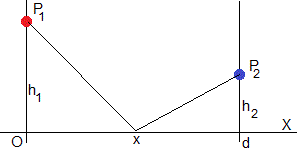
Dos farolas supuestas fuentes puntuales, que emiten luz en todas las direcciones y de forma isótropa, sus potencias son P₁ y P₂, respectivamente, están situadas a alturas h₁ y h₂ una enfrente de la otra en una calle de anchura d, tal como se muestra en la figura

Vamos a calcular y representar la intensidad de la luz I(x) en las posiciones x<d de la calle, debida a ambas fuentes y la posición del mínimo de dicha función.

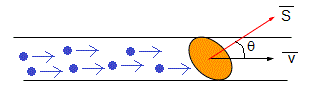
Al principio de esta página, se ha explicado el concepto de flujo, la energía por unidad de tiempo transportada por un movimiento ondulatorio armónico.

Supongamos que un conjunto de partículas se mueven con la misma velocidad $\overrightarrow{v}$, a lo largo de una tubería de sección normal S_n, el flujo es el producto v·S_n. Pero a través de la superficie S que forma un ángulo θ con S_n, el flujo es v·Scosθ, o el producto escalar, $\overrightarrow{v}·\overrightarrow{S}$

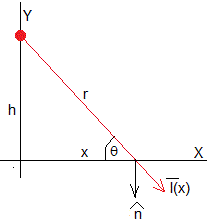
Como hemos visto la intensidad es inversamente proporcional al cuadrado de la distancia r a la fuente puntual, que emite en todas las direcciones de forma isótropa. Una lámpara de potencia P está situada a una altura h, ilumina una calle, la intensidad en un punto x, es

${\displaystyle I=\frac{P}{4\pi (x^2+h^2)}}$

La energía por unidad de tiempo (flujo) sobre un área dS cuya dirección es el vector unitario $\widehat{n}$ es el producto I·dS·cos(90-θ)=I·dS·sinθ. La intensidad de la luz medida en un punto x del la calle es

${\displaystyle I(x)=\frac{P}{4\pi (x^2+h^2)}\sin \theta =\frac{P}{4\pi }\frac{h}{{\left(x^2+h^2\right)}^{3/2}}}$

La intensidad en x debida a las dos farolas es

${\displaystyle I(x)=\frac{P_1}{4\pi }\frac{h_1}{{\left(x^2+h_1^2\right)}^{3/2}}+\frac{P_2}{4\pi }\frac{h_2}{{\left({\left(d-x\right)}^2+h_2^2\right)}^{3/2}}}$

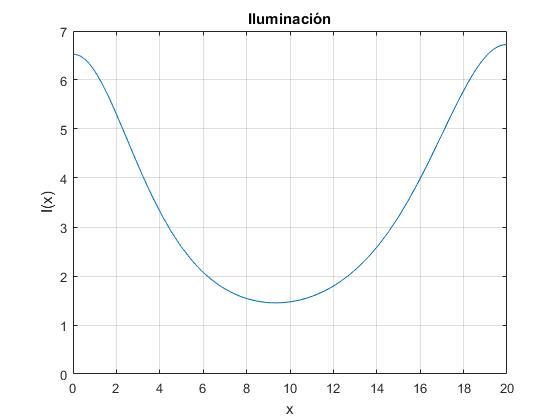
Supongamos que P₁=2000 W, P₂=3000 W, h₁=5 m, h₂=6 m y d=20 m. Representamos la intensidad en los puntos x comprendidos entre 0 y d

P1=2000; %potencia
P2=3000;
h1=5; %alturas
h2=6;
d=20; %anchura de la calle
f=@(x) (P1*h1./(x.^2+h1^2).^1.5+P2*h2./((d-x).^2+h2^2).^1.5)/(4*pi);
fplot(f,[0,d])
ylim([0,7])
grid on
xlabel('x')
ylabel('I(x)')
title('Iluminación')

Para hallar el mínimo, derivamos la función I(x) e igualamos a cero

${\displaystyle -\frac{P_1{h}_1·x}{{\left(x^2+h_1^2\right)}^{5/2}}+\frac{P_2{h}_2\left(d-x\right)}{{\left({\left(d-x\right)}^2+h_2^2\right)}^{5/2}}=0}$

Utilizamos la función fzero de MATLAB, para hallar la raíz

>> g=@(x) -P1*h1*x/(x^2+h1^2)^2.5+P2*h2*(d-x)/((d-x)^2+h2^2)^2.5;
>> fzero(g,[1,19])
ans =    9.3383

Elevamos al cuadrado y convertimos la expresión en un polinomio de grado doce

${\displaystyle {\left(P_1{h}_1·x\right)}^2{\left({\left(d-x\right)}^2+h_2^2\right)}^5-{\left(P_2{h}_2\left(d-x\right)\right)}^2{\left(x^2+h_1^2\right)}^5=0}$

Alternativamente, utilizamos Math Symbolic para representar gráficamente I(x) y calcular las raíces de la ecuación

>> syms P1 P2 h1 h2 d x;
>> Ix=(P1*h1/(x^2+h1^2)^1.5+P2*h2/((d-x)^2+h2^2)^1.5)/(4*pi);
>> Ix=subs(Ix,{P1,P2,h1,h2,d},{2000,3000,5,6,20})
>> ezplot(Ix,[0,20])

%derivada igual a cero
>> z=P1^2*h1^2*x^2*((d-x)^2+h2^2)^5-P2^2*h2^2*(d-x)^2*(x^2+h1^2)^5;
>> collect(z)
 ans = 
- 224000000*x^12 - 7040000000*x^11 + 1647900000000*x^10 - 
97260000000000*x^9 + 3544671000000000*x^8 - 88778520000000000*x^7 
+ 1552562031000000000*x^6 - 18794667480000000000*x^5 +
 150658331395500000000*x^4 - 722704471820000000000*x^3 + 
1575294640755100000000*x^2 + 126562500000000000*x - 1265625000000000000
>> solve(z)
ans =
 
                                       20.023104636951326959403464654848
                                        19.97669580711598127113382148871
                                    -0.028201701694406056112908556267141
                                     0.028489970379274335235724056424577
                                      -126.41496147220917462522617522851
                                        9.338299136346691141606386432591
 5.4322352441380728014228103397858*i + 9.1951777768138355026933758964326
 9.1951777768138355026933758964326 - 5.4322352441380728014228103397858*i
 24.542373306371245030188430411929*i + 5.0905190117153441171613123860283
 5.0905190117153441171613123860283 - 24.542373306371245030188430411929*i
 11.615790115575564042271671647107*i + 8.5383043087402595814108695793557
 8.5383043087402595814108695793557 - 11.615790115575564042271671647107*i

Hay tres raíces reales comprendidas entre 0 y d=20, solamente una raíz corresponde al mínimo x=9.338

Referencias

Alonso M., Finn E. J. Física. Addison-Wesley Iberoamericana (1995), págs. 644-646

Walter Gander, Jiri Hrebicek. Solving Problems in Scientific Computing Using Maple and MATLAB. Springer, 1997, pp.39-42