Frecuencias

La función de Planck en términos de la frecuencia f es

${\displaystyle B_f(T)df=\frac{2\pi h}{c^2}\frac{f^3}{\exp \left(hf/kT\right)-1}df}$

Estudiamos con más detalle la función que describe la intensidad (energía por unidad de área y unidad de tiempo) por unidad de frecuencia para la frecuencia f, de un cuerpo negro a la temperatura absoluta T.

Expresamos esta función en términos de la variable adimensional

${\displaystyle \begin{array}{l}x=\frac{hf}{kT}\\ B_x(T)dx=\frac{2\pi k^4{T}^4}{c^2{h}^3}\frac{x^3}{e^x-1}dx\\ {\sigma }^{*}=\frac{2\pi k^4{T}^4}{c^2{h}^3}=\frac{2\pi {\left(1.3805·{10}^{-23}\right)}^4}{{\left(2.9979·{10}^8\right)}^2{\left(6.6256·{10}^{-34}\right)}^3}{T}^4=8.7300·{10}^{-9}{T}^4\frac{\text{J}}{{\text{m}}^{\text{2}}\text{s}}\end{array}}$

La energía por unidad de tiempo y por unidad de área emitida a todas las frecuencias es

${\displaystyle \begin{array}{l}{B}_t={\displaystyle \underset{0}{\overset{\infty }{\int }}{B}_x}(T)dx={\sigma }^{*}{\displaystyle \underset{0}{\overset{\infty }{\int }}\frac{x^3}{e^x-1}dx=}{\sigma }^{*}\left(3!·\zeta (4)\right)=\frac{2\pi k^4{T}^4}{c^2{h}^3}6·\frac{{\pi }^4}{90}=\frac{2{\pi }^5{k}^4}{15c^2{h}^3}{T}^4\\ B_t=\sigma T^4\text{=5}{\text{.6692·10}}^{-8}{T}^4\end{array}}$

Esta es la ley de Stefan-Boltzmann. La energía emitida por un cuerpo negro por unidad de área y unidad de tiempo es proporcional a la cuarta potencia de la temperatura absoluta T.

La función ζ de Riemann

En esta página aparecen integrales de la forma

${\displaystyle {\displaystyle \underset{0}{\overset{\infty }{\int }}\frac{x^{n-1}}{e^x-1}}=\Gamma \left(n\right)\zeta \left(n\right)}$

Γ(n) es la función gamma, que para un argumento entero n es Γ(n)=(n-1)! y ζ(n) es la función ζ de Riemann. Sus primeros valores para el argumento n entero son

MATLAB proporciona la función zeta para calcular ζ(n)

>> for n=2:6
disp([n,zeta(n)])
end
    2.0000    1.6449
    3.0000    1.2021
    4.0000    1.0823
    5.0000    1.0369
    6.0000    1.0173

Máximo

Representamos la función

${\displaystyle f(x)=\frac{x^3}{e^x-1}}$

que tiene un máximo en x=2.8214

${\displaystyle \begin{array}{l}\frac{df(x)}{dx}=\frac{3x^2\left(e^x-1\right)-x^3{e}^x}{{\left(e^x-1\right)}^2}=0\\ \left(3x^2-x^3\right)e^x-3x^2=0\end{array}}$

solución de la ecuación transcendente que obtenemos utilizando fzero de MATLAB

f=@(x) x.^3./(exp(x)-1);
fplot(f,[0,8])
g=@(x) (3*x^2-x^3)*exp(x)-3*x^2;
%máximo
max=fzero(g,3);
line([max,max],[0,f(max)],'lineStyle','--')
ylim([0,1.5])
grid on
xlabel('x')
ylabel('f(x)')
title('Función de Planck')

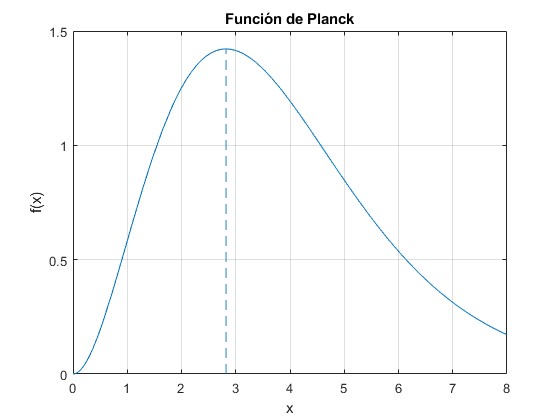
>> max
max =    2.8214

Anchura

La anchura de la función de Planck se define a partir de la desviación estándar Δf

${\displaystyle \Delta f=\sqrt{<f^2>-<f{>}^2}}$

Calculamos los valores medios

${\displaystyle \begin{array}{l}<f>=\frac{kT}{h}<x>\\ <x>=\frac{{\displaystyle \underset{0}{\overset{\infty }{\int }}x{B}_x(T)dx}}{{\displaystyle \underset{0}{\overset{\infty }{\int }}{B}_x(T)dx}}=\frac{{\sigma }^{*}{\displaystyle \underset{0}{\overset{\infty }{\int }}\frac{x^4}{e^x-1}dx}}{{\sigma }^{*}{\displaystyle \underset{0}{\overset{\infty }{\int }}\frac{x^3}{e^x-1}dx}}=\frac{4!·\zeta (5)}{3!·\zeta (4)}=\text{3}\text{.8322}\end{array}}$

>> 4*zeta(5)/zeta(4)
ans =    3.8322

La frecuencia media a la temperatura del Sol, T=5800 K

${\displaystyle <f>=<x>\frac{kT}{h}=\text{3}\text{.8322}\frac{\text{1}\text{.3805}·{10}^{-23}}{\text{6}\text{.6256}·{10}^{-34}}5800=\text{4}\text{.6312}·{10}^{14}\text{Hz}}$

que equivale a una longitud de onda de λ=c/f=6.4733·10^-7 m=647 nm

${\displaystyle \begin{array}{l}<f^2>=\frac{k^2{T}^2}{h^2}<x^2>\\ <x^2>=\frac{{\displaystyle \underset{0}{\overset{\infty }{\int }}{x}^2{B}_x(T)dx}}{{\displaystyle \underset{0}{\overset{\infty }{\int }}{B}_x(T)dx}}=\frac{{\sigma }^{*}{\displaystyle \underset{0}{\overset{\infty }{\int }}\frac{x^5}{e^x-1}dx}}{{\sigma }^{*}{\displaystyle \underset{0}{\overset{\infty }{\int }}\frac{x^3}{e^x-1}dx}}=\frac{5!\zeta (6)}{3!·\zeta (4)}\end{array}}$

La desviación estándar Δf es

${\displaystyle \Delta f=\frac{kT}{h}\Delta x=\frac{kT}{h}\sqrt{<x^2>-<x{>}^2}=\frac{kT}{h}\sqrt{20\frac{\zeta (6)}{\zeta (4)}-{\left(4\frac{\zeta (5)}{\zeta (4)}\right)}^2}=\text{ 2}\text{.0281}\frac{kT}{h}}$

>> sqrt(20*zeta(6)/zeta(4)-(4*zeta(5)/zeta(4))^2)
ans =    2.0281

Calculamos x₁ y x₂ de modo que

${\displaystyle \{\begin{array}{l}{x}_2-x_1=2\Delta x\\ f(x_2)=f(x_1)\end{array}}$

Resolvemos la ecuación transcendente en x₁

${\displaystyle \begin{array}{l}f\left(x_1+2\Delta x\right)-f(x_1)=0\\ \frac{{\left(x_1+2\Delta x\right)}^3}{\exp \left(x_1+2\Delta x\right)-1}-\frac{x_1^3}{\exp \left(x_1\right)-1}=0\end{array}}$

f=@(x) x.^3./(exp(x)-1);
fplot(f,[0,8])
g=@(x) (3*x^2-x^3)*exp(x)-3*x^2;
%máximo
max=fzero(g,3);
line([max,max],[0,f(max)],'lineStyle','--')
%anchura
Dx=sqrt(20*zeta(6)/zeta(4)-(4*zeta(5)/zeta(4))^2);
g=@(x) f(x+2*Dx)-f(x);
x1=fzero(g,max);
line([x1,x1],[0,f(x1)],'lineStyle','--')
x2=x1+2*Dx;
line([x2,x2],[0,f(x2)],'lineStyle','--')
line([x2,x1],[f(x2),f(x2)],'color','r')
ylim([0,1.5])
grid on
xlabel('x')
ylabel('f(x)')
title('Función de Planck')

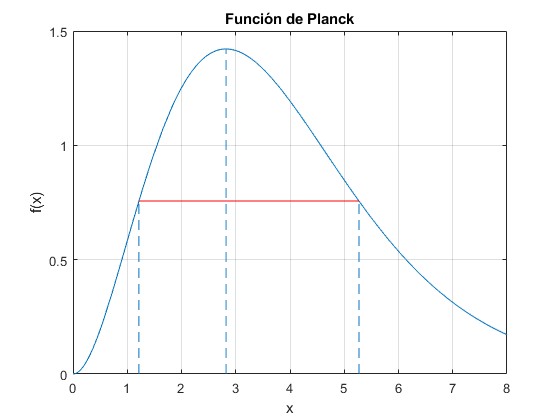
La anchura 2Δx se representa mediante una línea horizontal de color rojo trazada desde x₁ a x₂

>> x1,x2
x1 =    1.2147
x2 =    5.2709

La proporción de intensidad de la radiación emitida en esta región del espectro [x₁, x₂] es

${\displaystyle \frac{{\displaystyle \underset{x_1}{\overset{x_2}{\int }}{B}_x(T)dx}}{{\displaystyle \underset{0}{\overset{\infty }{\int }}{B}_x(T)dx}}=\frac{{\displaystyle \underset{x_1}{\overset{x_2}{\int }}\frac{x^3}{e^x-1}dx}}{3!·\zeta (4)}=0.7312}$

>> pro=integral(f,x1, x2)/(2*3*zeta(4))
pro =    0.7312

El intervalo [x₁, x₂] equivale a las frecuencias

${\displaystyle f_1=\frac{kT}{h}1.2147=\text{2}{\text{.5309·10}}^{10}T,f_2=\frac{kT}{h}5.2709=\text{1}{\text{.0982·10}}^{11}T}$

y a las longitudes de onda en nm

${\displaystyle {\lambda }_1=\frac{c}{f_1}=\frac{ch}{kT}\frac{{10}^9}{1.2147}=\frac{\text{1}{\text{.1845·10}}^7}{T}\text{nm},{\lambda }_2=\frac{c}{f_2}=\frac{ch}{kT}\frac{{10}^9}{5.2709}=\frac{\text{2}\text{.7297}·{10}^6}{T}\text{nm}}$

Para el Sol, T=5800 K, λ₁=2 042.3 nm y λ₂=470.6 nm

Número de fotones

La energía de un fotón es hf. El número de fotones por unidad de área y unidad de tiempo para la frecuencia f es

${\displaystyle \begin{array}{l}{N}_f(T)df=\frac{B_f(T)df}{hf}=\frac{2\pi }{c^2}\frac{f^2}{\exp \left(hf/kT\right)-1}df=\frac{2\pi }{c^2}\frac{\frac{k^2{T}^2}{h^2}{x}^2}{e^x-1}\frac{kT}{h}dx=\frac{2\pi k^3{T}^3}{c^2{h}^3}\frac{x^2}{e^x-1}dx\\ N_f(T)df=\text{6}{\text{.3238·10}}^{14}{T}^3\frac{x^2}{e^x-1}dx=\gamma \frac{x^2}{e^x-1}dx\\ N_x(T)=\gamma \frac{x^2}{e^x-1}\end{array}}$

Máximo

Representamos la función

${\displaystyle f(x)=\frac{x^2}{e^x-1}}$

que tiene un máximo en x=1.5936

${\displaystyle \begin{array}{l}\frac{df(x)}{dx}=\frac{2x\left(e^x-1\right)-x^2{e}^x}{{\left(e^x-1\right)}^2}=0\\ \left(2x-x^2\right)e^x-2x=0\end{array}}$

solución de la ecuación transcendente, obtenida utilizando fzero de MATLAB

f=@(x) x.^2./(exp(x)-1);
fplot(f,[0,8])
g=@(x) (2*x-x^2)*exp(x)-2*x;
%máximo
max=fzero(g,3);
line([max,max],[0,f(max)],'lineStyle','--')
ylim([0,0.7])
grid on
xlabel('x')
ylabel('f(x)')
title('Función de Planck')

>> max
max =    1.5936

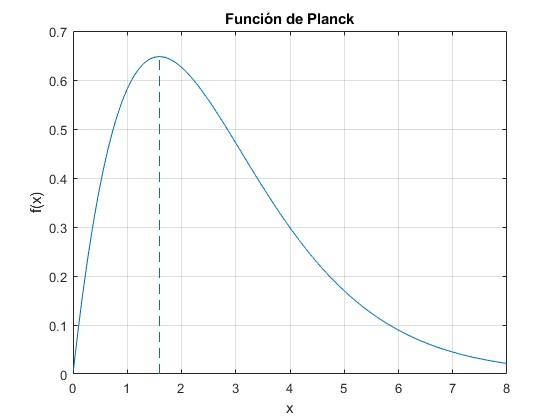
El número total de fotones N_p emitidos por unidad de área y de tiempo para todas las frecuencias

${\displaystyle \begin{array}{l}{N}_p={\displaystyle \underset{0}{\overset{\infty }{\int }}{N}_f(T)df=\text{6}{\text{.3238·10}}^{14}{T}^3{\displaystyle \underset{0}{\overset{\infty }{\int }}\frac{x^2}{e^x-1}dx=}}\text{6}{\text{.3238·10}}^{14}{T}^3\left(2!·\zeta (3)\right)\\ N_p=\text{1}{\text{.5203·10}}^{15}{T}^3\end{array}}$

Anchura

Calculamos los valores medios

${\displaystyle \begin{array}{l}<z>=\frac{{\displaystyle \underset{0}{\overset{\infty }{\int }}z{B}_z(T)dz}}{{\displaystyle \underset{0}{\overset{\infty }{\int }}{B}_z(T)dz}}=\frac{{\sigma }^{*}{\displaystyle \underset{0}{\overset{\infty }{\int }}\frac{z}{z^5\left(\exp \left(1/z\right)-1\right)}dz}}{{\sigma }^{*}{\displaystyle \underset{0}{\overset{\infty }{\int }}\frac{1}{z^5\left(\exp \left(1/z\right)-1\right)}dz}}=0.3702\\ <z^2>=\frac{{\displaystyle \underset{0}{\overset{\infty }{\int }}{z}^2{B}_z(T)dz}}{{\displaystyle \underset{0}{\overset{\infty }{\int }}{B}_z(T)dz}}=\frac{{\sigma }^{*}{\displaystyle \underset{0}{\overset{\infty }{\int }}\frac{z^2}{z^5\left(\exp \left(1/z\right)-1\right)}dz}}{{\sigma }^{*}{\displaystyle \underset{0}{\overset{\infty }{\int }}\frac{1}{z^5\left(\exp \left(1/z\right)-1\right)}dz}}=0.2533\end{array}}$

La desviación estándar Δf es

${\displaystyle \Delta f=\frac{kT}{h}\Delta x=\frac{kT}{h}\sqrt{<x^2>-<x{>}^2}=\frac{kT}{h}\sqrt{12\frac{\zeta (5)}{\zeta (3)}-{\left(3\frac{\zeta (4)}{\zeta (3)}\right)}^2}=\text{ 1}\text{.7479}\frac{kT}{h}}$

>> sqrt(12*zeta(5)/zeta(3)-(3*zeta(4)/zeta(3))^2)
ans =    1.7479

Calculamos x₁ y x₂ de modo que

${\displaystyle \{\begin{array}{l}{x}_2-x_1=2\Delta x\\ f(x_2)=f(x_1)\end{array}}$

Resolvemos la ecuación transcendente en x₁

${\displaystyle \begin{array}{l}f\left(x_1+2\Delta x\right)-f(x_1)=0\\ \frac{{\left(x_1+2\Delta x\right)}^2}{\exp \left(x_1+2\Delta x\right)-1}-\frac{x_1^2}{\exp \left(x_1\right)-1}=0\end{array}}$

f=@(x) x.^2./(exp(x)-1);
fplot(f,[0,8])
g=@(x) (2*x-x^2)*exp(x)-2*x;
%máximo
max=fzero(g,3);
line([max,max],[0,f(max)],'lineStyle','--')
%anchura
Dx=sqrt(12*zeta(5)/zeta(3)-(3*zeta(4)/zeta(3))^2);
g=@(x) f(x+2*Dx)-f(x);
x1=fzero(g,max);
line([x1,x1],[0,f(x1)],'lineStyle','--')
x2=x1+2*Dx;
line([x2,x2],[0,f(x2)],'lineStyle','--')
line([x2,x1],[f(x2),f(x2)],'color','r')
ylim([0,0.7])
grid on
xlabel('x')
ylabel('f(x)')
title('Función de Planck')

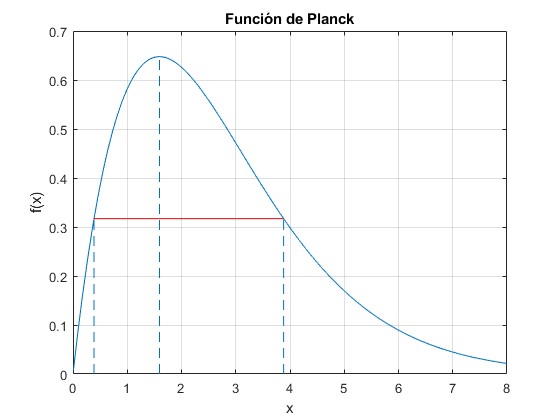
La anchura 2Δx se representa mediante una línea horizontal de color rojo trazada desde x₁ a x₂

>> x1,x2
x1 =    0.3871
x2 =    3.8829

La proporción del número de fotones emitidos en esta región del espectro [x₁, x₂] es

${\displaystyle \frac{{\displaystyle \underset{x_1}{\overset{x_2}{\int }}{N}_x(T)dx}}{{\displaystyle \underset{0}{\overset{\infty }{\int }}{N}_x(T)dx}}=\frac{{\displaystyle \underset{x_1}{\overset{x_2}{\int }}\frac{x^2}{e^x-1}dx}}{2!·\zeta (3)}=0.7582}$

>> pro=integral(f,x1, x2)/(2*zeta(3))
pro =    0.7582

El intervalo [x₁, x₂] equivale a las frecuencias

${\displaystyle f_1=\frac{kT}{h}0.3871=8.{\text{0656·10}}^{9}T,f_2=\frac{kT}{h}3.8829=\text{8}\text{.0904}·{10}^{10}T}$

y a las longitudes de onda en nm

${\displaystyle {\lambda }_1=\frac{c}{f_1}=\frac{ch}{kT}\frac{{10}^9}{0.3871}=\frac{\text{3}{\text{.7169·10}}^7}{T}\text{nm},{\lambda }_2=\frac{c}{f_2}=\frac{ch}{kT}\frac{{10}^9}{3.8829}=\frac{\text{3}\text{.7055}·{10}^6}{T}\text{nm}}$

Para el Sol, T=5800 K, λ₁=6 408.4 nm y λ₂=638.9 nm

Longitudes de onda

La función de Planck en términos de longitudes de onda es

${\displaystyle B_{\lambda }(T)d\lambda =\frac{2\pi h{c}^2}{{\lambda }^5}\frac{1}{\exp \left(hc/\lambda kT\right)-1}d\lambda }$

Estudiamos con más detalle la función que describe la intensidad (energía por unidad de área y unidad de tiempo) por unidad de longitud de onda para la longitud de onda λ, de un cuerpo negro a la temperatura absoluta T.

Expresamos esta función en términos de variable adimensional z

${\displaystyle \begin{array}{l}z=\frac{\lambda kT}{hc}\\ B_z(T)dz=\frac{2\pi h{c}^2}{\frac{h^5{c}^5}{k^5{T}^5}{z}^5}\frac{1}{\exp \left(1/z\right)-1}\frac{hc}{kT}dz={\sigma }^{*}\frac{1}{z^5\left(\exp \left(1/z\right)-1\right)}dz\end{array}}$

La constante σ^* se ha definido al principio de la página

Máximo

Representamos la función

${\displaystyle f(z)=\frac{1}{z^5\left(\exp \left(1/z\right)-1\right)}}$

que tiene un máximo en z=0.2014

${\displaystyle \begin{array}{l}\frac{df(z)}{dz}=0\\ \left(z^3-5z^4\right)\exp \left(\frac{1}{z}\right)+5z^4=0\end{array}}$

solución de la ecuación transcendente que obtenemos utilizando fzero de MATLAB

f=@(z) 1./(z.^5.*(exp(1./z)-1));
fplot(f,[0,1])
g=@(z) (z^3-5*z^4)*exp(1/z)+5*z^4;
%máximo
max=fzero(g,0.2);
line([max,max],[0,f(max)],'lineStyle','--')
ylim([0,22])
grid on
xlabel('z')
ylabel('f(z)')
title('Función de Planck')

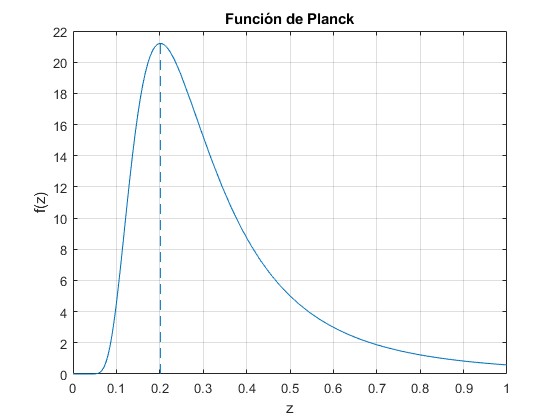
max
max =    0.2014

Anchura

Calculamos los valores medios

${\displaystyle \begin{array}{l}<z>=\frac{{\displaystyle \underset{0}{\overset{\infty }{\int }}z{B}_z(T)dz}}{{\displaystyle \underset{0}{\overset{\infty }{\int }}{B}_z(T)dz}}=\frac{{\sigma }^{*}{\displaystyle \underset{0}{\overset{\infty }{\int }}\frac{z}{z^5\left(\exp \left(1/z\right)-1\right)}dz}}{{\sigma }^{*}{\displaystyle \underset{0}{\overset{\infty }{\int }}\frac{1}{z^5\left(\exp \left(1/z\right)-1\right)}dz}}=0.3702\\ <z^2>=\frac{{\displaystyle \underset{0}{\overset{\infty }{\int }}{z}^2{B}_z(T)dz}}{{\displaystyle \underset{0}{\overset{\infty }{\int }}{B}_z(T)dz}}=\frac{{\sigma }^{*}{\displaystyle \underset{0}{\overset{\infty }{\int }}\frac{z^2}{z^5\left(\exp \left(1/z\right)-1\right)}dz}}{{\sigma }^{*}{\displaystyle \underset{0}{\overset{\infty }{\int }}\frac{1}{z^5\left(\exp \left(1/z\right)-1\right)}dz}}=0.2533\end{array}}$

Calculamos las integrales por procedimientos numéricos utilizando la función integral de MATLAB

>> f=@(z) z./(z.^5.*(exp(1./z)-1));
>> g=@(z) 1./(z.^5.*(exp(1./z)-1));
>> integral(f,0,inf)/integral(g,0,inf)
ans =    0.3702
>> f=@(z) z.^2./(z.^5.*(exp(1./z)-1));
>> integral(f,0,inf)/integral(g,0,inf)
ans =    0.2533

La desviación estándar Δz es

${\displaystyle \Delta z=\sqrt{<z^2>-<z{>}^2}=0.\text{341}0}$

>> sqrt(0.2533-0.3702^2)
ans =    0.3410

La desviación estándar Δλ es

${\displaystyle \Delta \lambda =\frac{hc}{kT}\Delta z=\frac{\text{4}\text{.9064}·{10}^6}{T}\text{nm}}$

Calculamos z₁ y z₂ de modo que

${\displaystyle \{\begin{array}{l}{z}_2-z_1=2\Delta z\\ f(z_2)=f(z_1)\end{array}}$

Resolvemos la ecuación transcendente en z₁

${\displaystyle \begin{array}{l}f\left(z_1+2\Delta z\right)-f(z_1)=0\\ \frac{1}{{\left(z_1+2\Delta z\right)}^5\exp \left(\frac{1}{z_1+2\Delta z}\right)-1}-\frac{1}{z_1^5\exp \left(\frac{1}{z_1}\right)-1}=0\end{array}}$

f=@(z) 1./(z.^5.*(exp(1./z)-1));
fplot(f,[0,1])
g=@(z) (z^3-5*z^4)*exp(1/z)+5*z^4;
%máximo
max=fzero(g,0.2);
line([max,max],[0,f(max)],'lineStyle','--')
% %anchura
Dz=0.3410;
g=@(z) f(z+2*Dz)-f(z);
z1=fzero(g,max);
line([z1,z1],[0,f(z1)],'lineStyle','--')
z2=z1+2*Dz;
line([z2,z2],[0,f(z2)],'lineStyle','--')
line([z2,z1],[f(z2),f(z2)],'color','r')
ylim([0,22])
grid on
xlabel('z')
ylabel('f(z)')
title('Función de Planck')

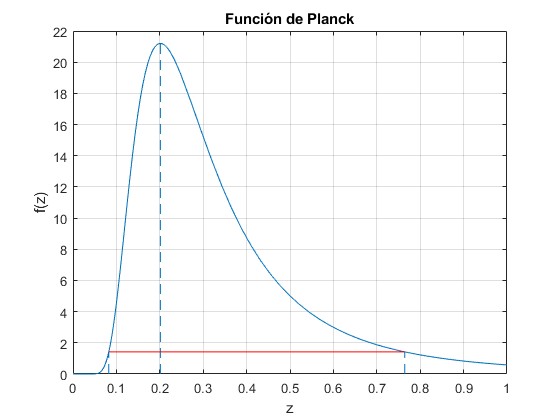
La anchura 2Δz se representa mediante una línea horizontal de color rojo trazada desde z₁ a z₂

>> z1,z2
z1 =    0.0825
z2 =    0.7645

que equivalen a las longitudes de onda en nm

${\displaystyle {\lambda }_1=\frac{hc}{kT}{z}_1=\frac{\text{1}\text{.1864}·{10}^6}{T}\text{nm}\text{,}{\lambda }_2=\frac{hc}{kT}{z}_2=\frac{\text{1}\text{.0999}·{10}^7}{T}\text{nm}}$

Para el Sol, T=5800 K, λ₁=204.5 nm y λ₂=1 896.4 nm

Referencias

B. Cameron Reed. Characterizing the breadth of the Planck function. Am. J. Phys. 93 (12), December 2025. pp. 1000-1004