Factorial de un número

Recordaremos en primer lugar, el concepto de factorial de un número entero positivo n.

n!=n·(n-1)·(n-2)...3·2·1

MATLAB dispone de una función denominada factorial, lo calculamos también con la función prod.

>> 1*2*3*4*5
ans =   120
>> factorial(5)
ans =   120
>> prod(1:5)
ans =   120

La función gamma

Se define del siguiente modo

${\displaystyle \Gamma (z)={\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-t}{t}^{z-1}dt}}$

Donde z puede ser un número real o complejo.

Esta función es más complicada en la parte negativa de z, tiene asíntotas verticales para z=0, -1, -2, -3...

syms x;
ezplot(gamma(x),[-4,5]), 
grid on

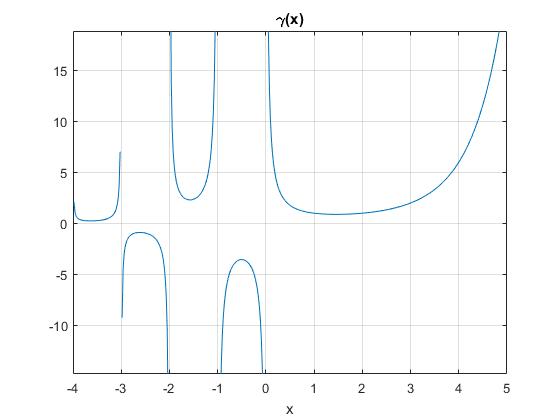
Representamos gráficamente la función gamma para z>0, llamando a la función del mismo nombre disponible en MATLAB.

>> fplot(@gamma,[0.1,4])
>> grid on
>> xlabel('x')
>> ylabel('\gamma(x)')
>> title('Función gamma')

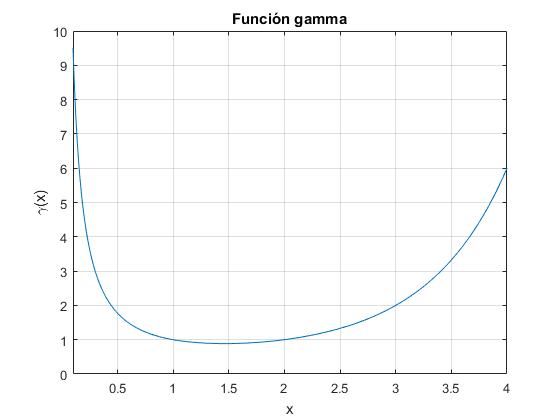
Calculamos el mínimo de la función aproximadamente.

>> x=1:0.01:2;
>> y=gamma(x);
>> yp=diff(y);
>> idx=find(abs(yp)<0.0001);
>> x(idx)
ans =    1.4500    1.4600
>> y(idx)
ans =    0.8857    0.8856

El mínimo se encuentra entre 1 y 2 en la posición x=1.46 y vale 0.8856.

Relaciones

Relacionamos Γ(z+1) con Γ(z)

${\displaystyle \Gamma (z+1)={\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-t}{t}^{z}dt}}$

Integrando por partes

${\displaystyle \begin{array}{l}{\displaystyle \int u·dv}=uv-{\displaystyle \int v·du}\\ u=t^{z}du=z{t}^{z-1}dt\\ dv=e^{-t}dtv=-e^{-t}\\ \Gamma (z+1)={\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-t}{t}^{z}dt}={\left[-e^{-t}{t}^z\right]}_0^{\infty }+z{\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-t}{t}^{z-1}dt}=z{\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-t}{t}^{z-1}dt}\\ \Gamma (z+1)=z\Gamma (z)z>0\end{array}}$

Mediante esta relación calculamos el valor de la función gamma, para z=1,2,3,4,...

${\displaystyle \begin{array}{l}\Gamma (1)={\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-t}dt}=1\\ \Gamma (2)=1·\Gamma (1)=1\\ \Gamma (3)=2·\Gamma (2)=2\\ \Gamma (4)=3·\Gamma (2)=6\\ \mathrm{.....}\\ \Gamma (n+1)=n·\Gamma (n)=n!\end{array}}$

>> z=1:6;
>> gamma(z)
ans =     1     1     2     6    24   120

Calculamos la función Γ(z) para valores fraccionarios de z. Por ejemplo, para z=1/2

${\displaystyle \Gamma (1/2)={\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-t}{t}^{-1/2}dt}}$

>> syms t;
>> y=exp(-t)/sqrt(t);
>> int(y,0,inf)
ans =pi^(1/2)

Para calcular el valor de la integral hacemos el cambio t=y².

${\displaystyle \Gamma (1/2)=2{\displaystyle \underset{0}{\overset{\infty }{\int }}\exp (-y^2)dy}}$

Se puede consultar en la tablas el valor de esta integral, o resolverla del siguiente modo

${\displaystyle I^2=\left({\displaystyle \underset{0}{\overset{\infty }{\int }}\exp }\left(-\alpha x^2\right)dx\right)\left({\displaystyle \underset{0}{\overset{\infty }{\int }}\exp }\left(-\alpha y^2\right)dy\right)={\displaystyle \underset{0}{\overset{\infty }{\int }}{\displaystyle \underset{0}{\overset{\infty }{\int }}\exp \left(-\alpha (x^2+y^2)\right)}}dx·dy}$

Cambiamos de coordenadas rectangulares a polares. En coordendas polares el elemento diferencial de área dx·dy=(r·dθ)dr

${\displaystyle \begin{array}{l}{x}^2+y^2=r^2\\ dx·dy=(r·d\theta )dr\\ {\displaystyle \underset{0}{\overset{\pi /2}{\int }}{\displaystyle \underset{0}{\overset{\infty }{\int }}\exp \left(-\alpha r^2\right)}}r·dr·d\theta =\frac{\pi }{2}{\displaystyle \underset{0}{\overset{\infty }{\int }}\exp \left(-\alpha r^2\right)·r·dr=\frac{\pi }{4\alpha }}\\ I={\displaystyle \underset{0}{\overset{\infty }{\int }}\exp }\left(-\alpha x^2\right)dx=\frac{1}{2}\sqrt{\frac{\pi }{\alpha }}\end{array}}$

Finalmente, utilizando la relación anterior Γ(z+1)=z·Γ(z)

${\displaystyle \begin{array}{l}\Gamma (1/2)=\sqrt{\pi }\\ \Gamma (3/2)=\frac{1}{2}\Gamma (1/2)=\frac{1}{2}\sqrt{\pi }\\ \mathrm{....}\\ \Gamma \left(n+\frac{1}{2}\right)=\frac{1·3·5···(2n-1)}{2^n}\sqrt{\pi }\end{array}}$

>> n=6;
>> num=2*(1:n)-1;
>> prod(num)*sqrt(pi)/2^n
ans =  287.8853
>> gamma(n+1/2)
ans =  287.8853

Fórmula de Euler

${\displaystyle \Gamma (z)\Gamma (1-z)=\frac{\pi }{\sin \left(\pi z\right)}}$

>> z=1.3;
>> gamma(z)*gamma(1-z)
ans =   -3.8832
>> pi/sin(pi*z)
ans =   -3.8832

La función beta

La función beta está relacionada con la función gamma

${\displaystyle B(m+\mathrm{1,}n+1)={\displaystyle \underset{0}{\overset{1}{\int }}{t}^m{\left(1-t\right)}^{n}dt=\frac{\Gamma (m+1)\Gamma (n+1)}{\Gamma (m+n+2)}}}$

Periodo de las oscilaciones

Consideremos una partícula de masa m oscilando a lo largo del eje X bajo la acción de una fuerza conservativa cuya energía potencial tiene la forma

${\displaystyle E_p(x)=b{\left|x\right|}^n,n\ne 2}$

b es un número real positivo y n suele ser un entero, pero puede ser un número real positivo

• El caso n=1, se ha estudiado en la página titulada Oscilaciones de una partícula bajo la acción de una fuerza de módulo constante.
• El caso n=2, corresponde a un oscilador armonico.
• El caso n=4, se ha estudiado en la página titulada Oscilador no lineal

Representamos la energía potencial E_p(x) entre -1.2<x<1.2, tomando b=1, para cada uno de los siguientes casos: n=1,2,3,4,5. Se trata de una función simétrica, por lo que solamente es necesario calcular los valores entre 0 y 1.2

x=linspace(0,1.2,200);
hold on
for n=1:5
    y=x.^n;
    yy=[fliplr(y),y];
    xx=[-fliplr(x),x];
    plot(xx,yy,'displayName',num2str(n))
end
hold off
legend('-DynamicLegend','location','best')
grid on
ylim([0,1.2])
xlabel('x')
ylabel('E_p(x)')
title('Energía potencial')

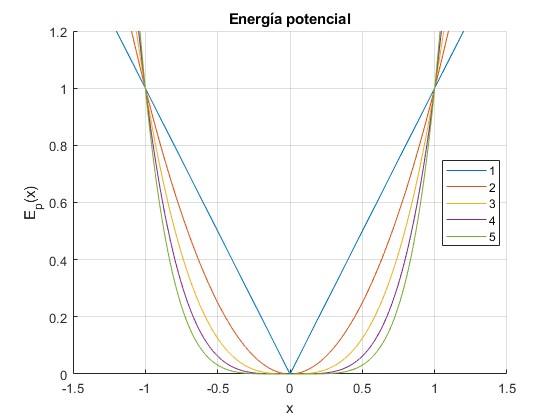
La energía constante E de la partícula es

${\displaystyle E=\frac{1}{2}m{\left(\frac{dx}{dt}\right)}^2+b{\left|x\right|}^n}$

Para calcular el periodo P de la oscilación despejamos dt e integramos

${\displaystyle \begin{array}{l}dt=\frac{dx}{\sqrt{\frac{2}{m}\left(E-b{\left|x\right|}^n\right)}}\\ P=4{\displaystyle \underset{0}{\overset{A}{\int }}\frac{dx}{\sqrt{\frac{2}{m}\left(E-b{x}^n\right)}}=}4\sqrt{\frac{m}{2E}}{\displaystyle \underset{0}{\overset{A}{\int }}\frac{dx}{\sqrt{1-\frac{b{x}^n}{E}}}},x\ge 0\end{array}}$

El periodo es cuatro veces el tiempo que tarda en desplazarse desde el origen hasta A, la amplitud de la oscilación, la posición en la que la velocidad dx/dt de la partícula es nula. E=bAⁿ

En el intervalo 0≤x≤A, x es positivo por lo que |x|=x

Para resolver la integral hacemos el cambio de variable

${\displaystyle \begin{array}{l}x={\left(\frac{E}{b}\right)}^{1/n}{\sin }^{2/n}\theta \\ dx={\left(\frac{E}{b}\right)}^{1/n}\frac{2}{n}{\sin }^{2/n-1}\theta \cos \theta ·d\theta \end{array}}$

Por otra parte,

${\displaystyle x^n=\frac{E}{b}{\sin }^2\theta }$

cuando x=A, sin²θ=1, θ=π/2

En términos de la nueva variable θ, el periodo se expresa

${\displaystyle P=\frac{8}{n}\sqrt{\frac{m}{2E}}{\left(\frac{E}{b}\right)}^{1/n}{\displaystyle \underset{0}{\overset{\pi /2}{\int }}{\sin }^{2/n-1}\theta ·d\theta }}$

Buscamos esta integral en una tabla de integrales, pág. 397, 3.621, n° 1

${\displaystyle {\displaystyle \underset{0}{\overset{\pi /2}{\int }}{\sin }^{\mu -1}\theta ·d\theta =2^{\mu -2}\text{B}}\left(\frac{\mu }{2},\frac{\mu }{2}\right)}$

con μ=2/n. Donde B es la función beta, teniendo en cuenta su relación con la función gamma

${\displaystyle B(m,n)=\frac{\Gamma (m)\Gamma (n)}{\Gamma (m+n)}}$

Obtenemos la fórmula del periodo en términos de la energía total E de la partícula

${\displaystyle P=\frac{8}{n}\sqrt{\frac{m}{2E}}{\left(\frac{E}{b}\right)}^{1/n}{2}^{{}^{2/n-2}}\frac{{\Gamma }^2\left(\frac{1}{n}\right)}{\Gamma \left(\frac{2}{n}\right)}=\frac{2^{{}^{2/n}}}{n}\sqrt{\frac{2m}{E}}{\left(\frac{E}{b}\right)}^{1/n}\frac{{\Gamma }^2\left(\frac{1}{n}\right)}{\Gamma \left(\frac{2}{n}\right)}}$

En términos de la amplitud A

${\displaystyle P=\frac{2^{{}^{2/n}}}{n}\sqrt{\frac{2m}{b}}{A}^{1-n/2}\frac{{\Gamma }^2\left(\frac{1}{n}\right)}{\Gamma \left(\frac{2}{n}\right)}}$

Representamos $\frac{P}{\sqrt{\frac{m}{b}}}$, en función de la amplitud A

hold on
for n=1:4
    f=@(x) 2^(2/n)*sqrt(2)*x.^(1-n/2)*gamma(1/n)^2/(n*gamma(2/n));
    fplot(f,[0,5],'displayName',num2str(n))
end
hold off
grid on
legend('-DynamicLegend','location','best')
ylim([0,25])
xlabel('A')
ylabel('P')
title('Periodo en función de la amplitud')

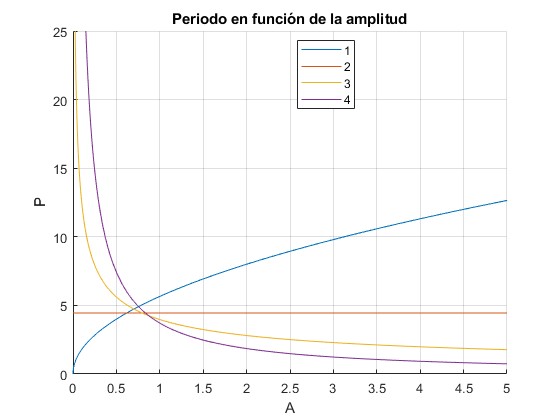
Para n=2, el periodo es independiente de la amplitud

Ejemplos

• Para n=1

${\displaystyle \begin{array}{l}\Gamma (1)=\Gamma (2)=1\\ P=4\sqrt{\frac{2m}{b}A}\end{array}}$

En la página titulada Oscilaciones de una partícula bajo la acción de una fuerza de módulo constante, b=f·m

${\displaystyle P=4\sqrt{\frac{2A}{f}}}$

• Para n=2

Para el sistema formado por una masa m unida a un muelle elástico de constante k, E_p(x)=kx²/2, por lo que b=k/2

${\displaystyle \begin{array}{l}\Gamma (1)=1\\ \Gamma \left(\frac{1}{2}\right)=\sqrt{\pi }\\ P=\sqrt{\frac{2m}{b}}\frac{\pi }{1}=2\pi \sqrt{\frac{m}{k}}\end{array}}$

• Para n=4

La energía potencial correspondiente a la fuerza conservativa proporcional a x³ es

${\displaystyle E_p(x)=\frac{1}{4}\frac{k}{l_0^2}{x}^4,b=\frac{1}{4}\frac{k}{l_0^2}}$

El periodo es

${\displaystyle P=\frac{l_0}{A}\sqrt{\frac{m}{k}}\frac{{\Gamma }^2\left(\frac{1}{4}\right)}{\sqrt{\pi }}}$

En la página titulada Oscilador no lineal, obtuvimos la fórmula del periodo

${\displaystyle P=4\frac{l_0}{A}\sqrt{\frac{m}{k}}K\left(\frac{1}{\sqrt{2}}\right)}$

Comprobamos que dan el mismo resultado

>> 4*ellipke(1/2)
ans =    7.4163
>> gamma(1/4)^2/sqrt(pi)
ans =    7.4163

Ejemplos en el Curso de Física

Vaciado de un depósito abierto.

Referencias

Special functions and their applications. N.N. Lebedev. Prentice Hall Inc. 1965

Anyi Amezquita, María Delgado, Diego Rasero. Sistemas oscilantes intrínsecamente no lineales. Revista Brasileira de Ensino de Física, vol. 43, e20210110 (2021)

Pirooz Mohazzabi. Theory and examples of intrinsically nonlinear oscillators. Am. J. Phys. 72 (4), April 2004, pp. 492-498

I. S. Gradshteyn, I. M. Ryzhik. Table of Integrals, Series, and Products. Seventh Edition. Elsevier (2007). Pág. 397, 3.621, n° 1