La entropía

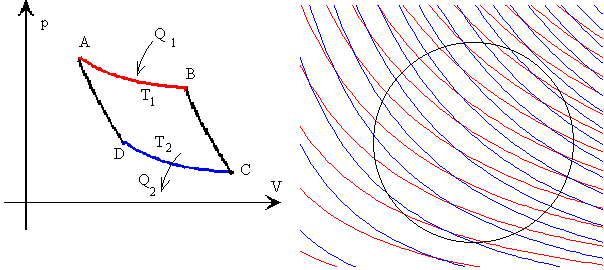
En un ciclo reversible de Carnot siempre se cumple

$\frac{Q_{1}}{T_{1}} + \frac{Q_{2}}{T_{2}} = 0$

Se puede aproximar un ciclo reversible cualesquiera (en color negro) por una línea discontinua en forma de diente de sierra formada por adiabáticas (color azul) e isotermas (color rojo) tal como se muestra en la figura.

Se cumplirá entonces que

$\sum \frac{Q_{i}}{T_{i}} = 0$

Si los ciclos son infinitesimales, entonces

$\oint \frac{δ Q}{T} = 0$

Se define entropía como una función de estado y por lo tanto, la variación de entropía a lo largo de un camino cerrado es 0

$d S = \frac{δ Q}{T}$

Las variaciones de entropía en la transformación 1-2 es

$S_{2} - S_{1} = \int_{1}^{2} \frac{δ Q}{T}$

Si la temperatura T es constante, la variación de entropía es el cociente entre el calor y la temperatura.

$S_{2} - S_{1} = \frac{Q_{12}}{T}$

En un ciclo reversible, la variación de entropía es cero. En todo proceso irreversible la variación de entropía es mayor que cero.

La Segunda ley afirma que la entropía de un sistema aislado nunca puede decrecer. Cuando un sistema aislado alcanza una configuración de máxima entropía, ya no puede experimentar cambios: ha alcanzado el equilibrio.

Variaciones de entropía en procesos irreversibles

Para calcular las variaciones de entropía de un proceso real (irreversible) hemos de recordar que la entropía (como la energía interna) depende solamente del estado del sistema. Una variación de entropía cuando el sistema pasa de un estado A a otro B de equilibrio depende solamente del estado inicial A y del estado final B.

Para calcular la variación de entropía ΔS de un proceso irreversible entre dos estados de equilibrio, imaginamos un proceso reversible entre el estado inicial A y el estado final B y calculamos para este proceso

$Δ S = \int_{A}^{B} \frac{d Q}{T}$

Como veremos en los ejemplo, la variación de entropía ΔS es siempre positiva para el sistema y sus alrededores en un proceso irreversible.

La entropía de un sistema aislado que experimenta un cambio siempre se incrementa. En un proceso reversible la entropía del sistema aislado permanece constante.

Cambio de estado

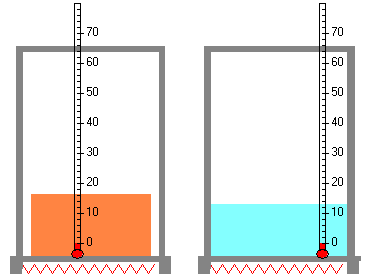
Un sólido cuyo calor de fusión es L_f funde a la temperatura T_f. Calcular la variación de entropía cuando una masa m de sólido.

En el proceso de cambio de estado, una sustancia absorbe una cantidad de calor mL_f manteniendo la temperatura constante T_f

$Δ S = \frac{m L_{f}}{T_{f}}$

Calorímetro de mezclas

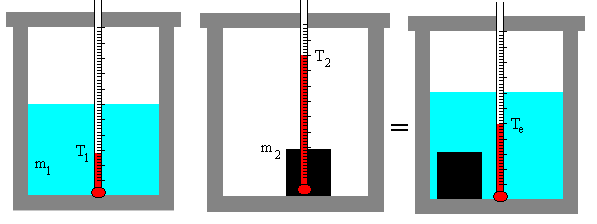
En un calorímetro de mezclas, una sustancia de masa m₁, calor específico c₁ y temperatura inicial T₁ se coloca en contacto con una segunda sustancia de masa m₂, calor específico c₂ y temperatura inicial T₂>T₁. Las dos sustancias se colocan en un calorímetro de modo que forman ambas un sistema aislado. Una vez que alcanzan el equilibrio térmico a la temperatura T_e vamos a calcular la variación de entropía.

La sustancia que inicialmente tiene la temperatura mas alta cede calor a la sustancia que inicialmente tiene temperatura más baja, la primera disminuye su temperatura, la segunda la aumenta hasta que ambas alcanzan el equilibrio a la temperatura T_e.

m₁·c₁·(T_e-T₁)+m₂·c₂·(T_e-T₂)=0

$T_{e} = \frac{m_{1} c_{1} T_{1} + m_{2} c_{2} T_{2}}{m_{1} c_{1} + m_{2} c_{2}}$

El proceso es irreversible por que el sistema evoluciona desde el estado inicial al final a través de una serie de estados de no equilibrio.

Para calcular la variación de entropía, imaginamos que la sustancia que tiene la temperatura más alta T₁ se enfría hasta una temperatura T_e poniéndola en contacto sucesivamente con focos de calor que difieren infinitesimalmente en temperatura, el primer foco tiene una temperatura T₂ y el último T_e. Podemos imaginar un proceso similar para la sustancia inicialmente a menor temperatura T₂.

El calor absorbido o cedido en un cambio infinitesimal de temperatura es, dQ=mcdT

$\begin{array}{l} Δ S = \int \frac{d Q_{1}}{T} + \int \frac{d Q_{2}}{T} = m_{1} c_{1} \int_{T_{1}}^{T_{e}} \frac{d T}{T} + m_{2} c_{2} \int_{T_{2}}^{T e} \frac{d T}{T} = \\ m_{1} c_{1} \ln (\frac{T_{e}}{T_{1}}) + m_{2} c_{2} \ln (\frac{T_{e}}{T_{2}}) \end{array}$

Como T_e>T₁ el primer término es positivo, y como T_e<T₂ el segundo término es negativo, el resultado final es que ΔS>0

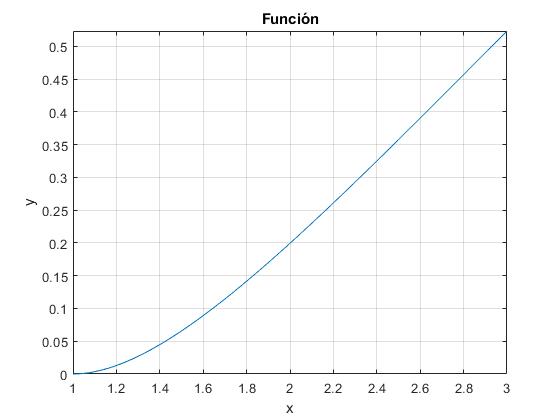
Comprobación: llamamos k=m₁c₁/(m₂c₂) y x=T₂/T₁>1

$\begin{array}{l} \frac{T_{e}}{T_{2}} = \frac{\frac{m_{1} c_{1}}{x} + m_{2} c_{2}}{m_{1} c_{1} + m_{2} c_{2}} = \frac{1}{x} \frac{k + x}{k + 1} \\ \frac{T_{e}}{T_{1}} = \frac{k + x}{k + 1} \\ Δ S = m_{1} c_{1} \ln (\frac{k + x}{k + 1}) - m_{2} c_{2} \ln x + m_{2} c_{2} \ln (\frac{k + x}{k + 1}) = (m_{1} c_{1} + m_{2} c_{2}) \ln (\frac{k + x}{k + 1}) - m_{2} c_{2} \ln x \\ Δ S = m_{2} c_{2} {(k + 1) \ln (\frac{k + x}{k + 1}) - \ln x} \end{array}$

Esta función es positiva para k>0 y x>1

k=3;
f=@(x) (k+1)*log((k+x)/(k+1))-log(x);
fplot(f,[1,3])
grid on
xlabel('x')
ylabel('y')
title('Función')

Una demostración más rigurosa se encuentra en el artículo de Lima, mencionado en las referencias

Caso particular

Sean dos bloques idénticos hechos del mismo material a las temperaturas T₁ y T₂ en el interior de un recinto térmicamente aislado. Se ponen en contacto, la temperatura final de equilibrio es la media aritmética, T_e=(T₁+T₂)/2. El cambio de entropía es

$Δ S = m c (2 \ln T_{e} - \ln (T_{1} T_{2})) = 2 m c (\ln (\frac{T_{1} + T_{2}}{2}) - \ln (\sqrt{T_{1} T_{2}}))$

La media aritmética es siempre mayor que la geométrica, por lo que ΔS>0

Expansión de un gas

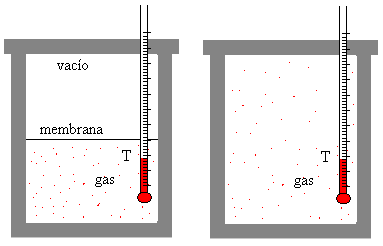
Consideremos la expansión adiabática de un gas ideal que ocupa inicialmente un volumen V₁. Se rompe la membrana que separa el gas de la región en la que se ha hecho el vacío, el gas se expande irreversiblemente hasta ocupar un volumen V₂.

El trabajo realizado por el gas es cero W=0, ya que las paredes del recipiente son aislantes, no se transfiere energía hacia el exterior, Q=0

Como la energía interna no cambia ΔU=0, la temperatura no cambia, ya que la energía interna de un gas ideal solamente depende de la temperatura T.

Para calcular la variación de entropía, imaginamos un proceso reversible isotérmico a la temperatura T en la que el gas empuje muy despacio el émbolo mientras la energía entra en el gas procedente de un foco de calor para mantener la temperatura constante.

$Δ S = \int \frac{d Q}{T} = \frac{1}{T} \int d Q$

En un proceso isotérmico, no hay variación de energía interna, el primer principio implica que el calor absorbido es igual al trabajo realizado por el gas durante su expansión de V₁ a V₂.

dQ=dW=pdV

$Δ S = \frac{1}{T} \int_{V_{1}}^{V_{2}} p d V = \int_{V_{1}}^{V_{2}} \frac{n R}{V} d V = n R \ln \frac{V_{2}}{V_{1}}$

Como V₂>V₁ se concluye que ΔS>0

Referencias

F.M.S. Lima. Change of entropy in the spontaneous thermalization of two distinct blocks. Revista Brasileira de Ensino de Física, v. 37, n. 1, 1701 (2015). https://www.scielo.br/j/rbef/i/2015.v37n1/