La ecuación de Schrödinger unidimensional e independiente del tiempo es

${\displaystyle \frac{-{\hslash }^2}{2m}\frac{d^2\Psi }{d{x}^2}+E_p(x)\Psi =E\Psi }$

La energía potencial de un oscilador armónico es E_p(x)=kx²/2, donde k es la constante elástica y m la masa de la partícula.

Tomando una escala de energías y distancias de la forma

${\displaystyle x=\xi \sqrt{\frac{\hslash }{m\omega }}E=\hslash \omega \epsilon \omega =\sqrt{\frac{k}{m}}}$

La ecuación de Schrödinger se transforma en otra más simple

${\displaystyle \frac{d^2\psi (\xi )}{d{\xi }^2}+\left(2\epsilon -{\xi }^2\right)\psi (\xi )=0}$

Haciendo un cambio de variable, la ecuación diferencial se transforma en la de Hermite

${\displaystyle \begin{array}{l}\psi (\xi )=y(\xi )\exp \left(-\frac{{\xi }^2}{2}\right)\\ \frac{d\psi }{d\xi }=\exp \left(-\frac{{\xi }^2}{2}\right)\frac{dy}{d\xi }-\xi \exp \left(-\frac{{\xi }^2}{2}\right)y\\ \frac{d^2\psi }{d{\xi }^2}=\exp \left(-\frac{{\xi }^2}{2}\right)\frac{d^{2}y}{d{\xi }^2}-\xi \exp \left(-\frac{{\xi }^2}{2}\right)\frac{dy}{d\xi }-\exp \left(-\frac{{\xi }^2}{2}\right)y+{\xi }^2\exp \left(-\frac{{\xi }^2}{2}\right)y-\xi \exp \left(-\frac{{\xi }^2}{2}\right)\frac{dy}{d\xi }\\ \frac{d^{2}y}{d{\xi }^2}-2\xi \frac{dy}{d\xi }+\left(2\epsilon -1\right)y=0\end{array}}$

Cuya solución son los polinomios de Hermite

${\displaystyle \begin{array}{l}2\epsilon -1=2n\hfill \\ y(\xi )=C·H_n(\xi )\hfill \end{array}}$

Los niveles de energía y las funciones de onda son

${\displaystyle \begin{array}{l}{\epsilon }_n=n+\frac{1}{2},n=\mathrm{0,1,2,3...}\hfill \\ {\psi }_n(\xi )=C·H_n(\xi )\exp \left(-\frac{{\xi }^2}{2}\right)\hfill \end{array}}$

La constante C se determina haciendo que

${\displaystyle \begin{array}{l}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}|{\psi }_n(\xi ){|}^{2}d\xi }=1\hfill \\ \begin{array}{l}{C}^2{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{H}_n^2(\xi )\exp (-{\xi }^2)d\xi }=1\\ C^2\sqrt{\pi }{2}^{n}n!=1\end{array}\hfill \end{array}}$

Se ha tenido en cuenta las relaciones de ortogonalidad de los polinomios de Hermite. El resultado final es

${\displaystyle \begin{array}{l}{\psi }_n(\xi )=\frac{H_n(\xi )}{\sqrt{2^n\sqrt{\pi }n!}}\exp \left(-\frac{{\xi }^2}{2}\right)\\ {\epsilon }_n=n+\frac{1}{2},n=\mathrm{0,1,2,3...}\end{array}}$

Representamos el nivel de energía ε_n y la función de onda correspondiente a n=3

n=3; %estado (cambiar), 1,2,3,4...
hold on
x=-4:0.1:4;
y=x.^2/2;
xx=[-4 x 4];
yy=[0 y 0];
fill(xx,yy,[0.5 0.5 0.5])
plot(x,y,'b')
line([-4 4],[n+0.5 n+0.5], 'color','k')
y=n+0.5+hermiteH(n,x).*exp(-x.^2/2)/sqrt(2^n*sqrt(pi)*factorial(n));
plot(x,y,'r') 
hold off
grid on
xlabel('x')
ylabel('\Phi(x)')
title('Oscilador armónico cuántico')

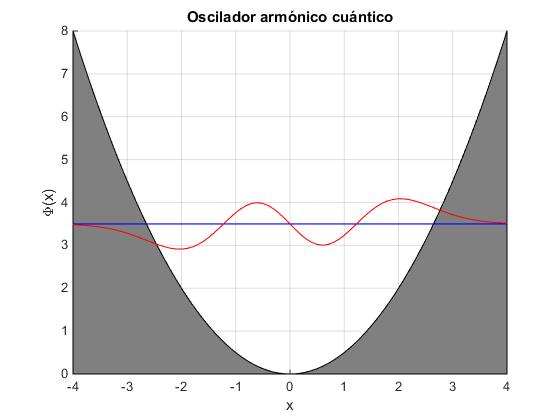
Los niveles de energía y las funciones de onda en términos de la variable x

${\displaystyle \begin{array}{l}{E}_n=\hslash \omega \left(n+\frac{1}{2}\right),n=\mathrm{0,1,2,3...}\\ {\psi }_n(x)=C·H_n\left(\sqrt{\frac{m\omega }{\hslash }}x\right)\exp \left(-\frac{m\omega }{2\hslash }{x}^2\right)\end{array}}$

La constante C se determina haciendo que

${\displaystyle \begin{array}{l}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}|{\psi }_n(x){|}^{2}dx}=1\hfill \\ C^2{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{H}_n^2\left(\sqrt{\frac{m\omega }{\hslash }}x\right)\exp \left(-\frac{m\omega }{\hslash }{x}^2\right)dx=1}\hfill \end{array}}$

Hacemos el cambio de variable

${\displaystyle \begin{array}{l}z=\sqrt{\frac{m\omega }{\hslash }}x\hfill \\ C^2\sqrt{\frac{\hslash }{m\omega }}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{H}_n^2(z)\exp (-z^2)dz}=1\hfill \\ C^2\sqrt{\frac{\hslash }{m\omega }}{2}^{n}n!\sqrt{\pi }=1\hfill \end{array}}$

El resultado final es

${\displaystyle {\psi }_n(x)={\left(\frac{m\omega }{\pi \hslash }\right)}^{1/4}\frac{1}{\sqrt{2^{n}n!}}{H}_n\left(\sqrt{\frac{m\omega }{\hslash }}x\right)\exp \left(-\frac{m\omega }{2\hslash }{x}^2\right)}$