El problema de dos cuerpos

Consideremos ahora un sistema aislado formado por dos cuerpos: un cuerpo de masa m₁ y otro cuerpo de masa m₂ bajo la acción de la fuerza de atracción mutua.

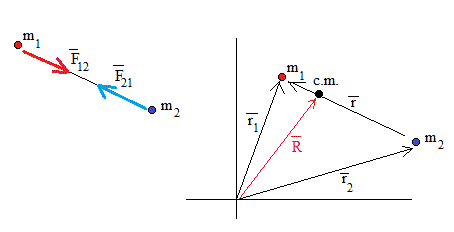
Por la tercera ley de Newton la fuerza con que atrae el cuerpo 1 al 2 es igual y de sentido contrario a la fuerza con que atrae el cuerpo 2 al 1.

$\begin{array}{l} \vec{F_{12}} = - F_{21} \hat{r} = - G \frac{m_{1} m_{2}}{r^{2}} \hat{r} \\ \vec{r} = \vec{r_{1}} - \vec{r_{2}} \hat{r} = \frac{\vec{r}}{r} \end{array}$

Cada cuerpo se mueve bajo la fuerza de atracción mutua

$m_{1} \frac{d^{2} \vec{r_{1}}}{d t^{2}} = \vec{F_{12}} m_{2} \frac{d^{2} \vec{r_{2}}}{d t^{2}} = \vec{F_{21}}$

Restamos miembro a miembro las dos ecuaciones diferenciales

$\begin{array}{l} \frac{\vec{F_{12}}}{m_{1}} - \frac{\vec{F_{21}}}{m_{2}} = \frac{d^{2} \vec{r_{1}}}{d t^{2}} - \frac{d^{2} \vec{r_{2}}}{d t^{2}} \\ - G \frac{m_{1} m_{2}}{r^{2}} \hat{r} (\frac{1}{m_{1}} + \frac{1}{m_{2}}) = \frac{d^{2} \vec{r}}{d t^{2}} \\ - G \frac{m_{1} m_{2}}{r^{2}} \hat{r} = μ \frac{d^{2} \vec{r}}{d t^{2}} μ = \frac{m_{1} m_{2}}{m_{1} + m_{2}} \end{array}$

Obtenemos una única ecuación diferencial que describe el movimiento de un cuerpo de masa reducida μ bajo la acción de la fuerza de atracción entre los dos cuerpos

Las posiciones del centro de masas (c.m.) y de cada una de las partículas vienen dadas por las siguientes expresiones

$\begin{array}{l} \vec{R} = \frac{m_{1} \vec{r_{1}} + m_{2} \vec{r_{2}}}{m_{1} + m_{2}}, \vec{r} = \vec{r_{1}} - \vec{r_{2}} \\ \vec{r_{1}} = \vec{R} + \frac{m_{2}}{m_{1} + m_{2}} \vec{r}, \vec{r_{2}} = \vec{R} - \frac{m_{1}}{m_{1} + m_{2}} \vec{r} \end{array}$

De modo similar, obtenemos la velocidad del c.m. y de cada una de las partículas

$\begin{array}{l} \vec{V_{c m}} = \frac{m_{1} \vec{v_{1}} + m_{2} \vec{v_{2}}}{m_{1} + m_{2}}, \vec{v} = \vec{v_{1}} - \vec{v_{2}} \\ \vec{v_{1}} = \vec{V_{c m}} + \frac{m_{2}}{m_{1} + m_{2}} \vec{v}, \vec{v_{2}} = \vec{V_{c m}} - \frac{m_{1}}{m_{1} + m_{2}} \vec{v} \end{array}$

Siendo la velocidad relativa $\vec{v} = \vec{v_{1}} - \vec{v_{2}}$ de las partículas

Escribimos la energía cinética en términos de la velocidad del c.m. V_cm y la velocidad relativa de las partículas v

$E_{k} = \frac{1}{2} m_{1} v_{1}^{2} + \frac{1}{2} m_{2} v_{2}^{2} = \frac{1}{2} (m_{1} + m_{2}) V_{c m}^{2} + \frac{1}{2} \frac{m_{1} m_{2}}{m_{1} + m_{2}} v^{2}$

La energía relativa al c.m. es

$E_{c m} = \frac{1}{2} μ v^{2} - G \frac{m_{1} m_{2}}{r}$

El momento angular respecto del origen O vale

$\begin{array}{l} \vec{L} = \vec{r_{1}} \times m_{1} \vec{v_{1}} + \vec{r_{2}} \times m_{2} \vec{v_{2}} = \\ (\vec{R} + \frac{m_{2}}{m_{1} + m_{2}} \vec{r}) \times m_{1} (\vec{V_{c m}} + \frac{m_{2}}{m_{1} + m_{2}} \vec{v}) + (\vec{R} - \frac{m_{1}}{m_{1} + m_{2}} \vec{r}) \times m_{2} (\vec{V_{c m}} - \frac{m_{1}}{m_{1} + m_{2}} \vec{v}) \\ = \vec{R} \times (m_{1} + m_{2}) \vec{V_{c m}} + \vec{r} \times \frac{m_{1} m_{2}}{m_{1} + m_{2}} \vec{v} \end{array}$

El momento angular relativo al c.m. es

$\vec{L_{c m}} = \vec{r} \times μ \vec{v}$

En el sistema de referencia del centro de masa el problema de dos cuerpos se reduce al problema de un solo cuerpo de masa μ, bajo la acción de la fuerza de atracción mutua entre las dos partículas. La energía y el momento angular se escriben en coordenadas polares

$\begin{array}{l} E_{c m} = \frac{1}{2} μ {(\frac{d r}{d t})}^{2} + \frac{L_{c m}^{2}}{2 μ r^{2}} - G \frac{m_{1} m_{2}}{r} \\ L_{c m} = μ r^{2} \frac{d θ}{d t} \end{array}$

Eliminamos el tiempo e integramos para obtener la ecuación de la trayectoria en coordenadas polares

$\frac{d θ}{d r} = \frac{\frac{L_{c m}}{μ r^{2}}}{\sqrt{\frac{2}{μ} (E_{c m} - \frac{L_{c m}^{2}}{2 μ r^{2}} + \frac{G m_{1} m_{2}}{r})}}$

Seguimos los mismos pasos que en la página previa Ecuación de la trayectoria y obtenemos

$\begin{array}{l} \frac{1}{r} - \frac{b}{2 a} = \sqrt{\frac{c}{a} + \frac{b^{2}}{4 a^{2}}} \cos θ \\ a = \frac{L_{c m}^{2}}{2 μ} b = G m_{1} m_{2} c = E_{c m} \\ r = \frac{d}{1 + ε \cos θ} \\ d = \frac{2 a}{b} = \frac{L_{c m}^{2}}{μ G m_{1} m_{2}} ε = \sqrt{1 + \frac{4 a c}{b^{2}}} = \sqrt{1 + \frac{2 L_{c m}^{2} E_{c m}}{μ {(G m_{1} m_{2})}^{2}}} \end{array}$

Para una órbita elíptica, ε<1, calculamos el semieje mayor a y el semieje menor b, y a continuación el periodo P

$\begin{array}{l} 2 a = \frac{d}{1 + ε} + \frac{d}{1 - ε} a = \frac{d}{1 - ε^{2}} = - \frac{G m_{1} m_{2}}{2 E_{c m}} \\ b = \sqrt{a^{2} - c^{2}} = a \sqrt{1 - ε^{2}} = \sqrt{a} \frac{L_{c m}}{\sqrt{μ G m_{1} m_{2}}} \\ P = \frac{2 π μ a b}{L_{c m}} = \frac{2 π \sqrt{μ} a^{\frac{3}{2}}}{\sqrt{G m_{1} m_{2}}} P^{2} = \frac{4 π^{2}}{G (m_{1} + m_{2})} a^{3} \end{array}$

En el caso del sistema aislado formado por la Tierra cuya masa es 5.98·10²⁴ kg y un satélite artificial, la masa de la Tierra es muchísimo mayor que la del satélite. Consideraremos la Tierra como un centro fijo de fuerzas

En el caso del sistema Tierra-Sol, la masa del Sol es 1.98·10³⁰ kg, la distancia entre el centro de la Tierra y del Sol es 149.6·10⁹ m. La posición del centro de masa del sistema medido desde el centro del Sol es

$x_{c} = \frac{5.98 \cdot 10^{24} \cdot 149.6 \cdot 10^{9}}{5.98 \cdot 10^{24} + 1.98 \cdot 10^{30}} = 0.452 \cdot 10^{6} m$

Que está en el interior del Sol cuyo radio es 696·10⁶ m. Consideraremos el Sol como un centro fijo de fuerzas.

Ejemplo

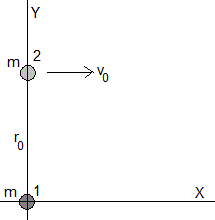
Estudiamos el sistema aislado formado por dos partículas de la misma masa m, separadas inicialmente una distancia r₀. La primera masa está inicialmente en reposo en el origen, la velocidad inicial de la segunda es v₀.

Vamos a determinar las trayectorias de las partículas bajo la acción de su interacción mutua.

Movimiento del centro de masas

La posición del centro de masas es

$\vec{R} = \frac{m r_{0} \hat{j}}{m + m} = \frac{r_{0}}{2} \hat{j}$

La velocidad del centro de masas

$\vec{V_{c m}} = \frac{m v_{0} \hat{i}}{m + m} = \frac{v_{0}}{2} \hat{i}$

Al ser un sistema aislado, el centro de masas se mueve con velocidad constante v₀/2, a lo largo de la recta y=r₀/2.

Movimiento relativo

La posición inicial relativa es

$\vec{r} = \vec{r_{1}} - \vec{r_{2}} = - d \hat{j}$

La velocidad inicial relativa es

$\vec{v} = \vec{v_{1}} - \vec{v_{2}} = - v_{0} \hat{i}$

La energía del sistema relativa al c.m. es

$\begin{array}{l} E_{c m} = \frac{1}{2} μ v^{2} - G \frac{m_{1} m_{2}}{r}, μ = \frac{m_{1} m_{2}}{m_{1} + m_{2}} \\ E_{c m} = \frac{1}{4} m v_{0}^{2} - G \frac{m^{2}}{r_{0}} \end{array}$

El momento angular del sistema relativo al c.m. es

$\begin{array}{l} \vec{L_{c m}} = \vec{r} \times μ \vec{v} \\ \vec{L_{c m}} = - r_{0} \hat{j} \times \frac{m}{2} (- v_{0} \hat{i}) = - \frac{m}{2} v_{0} r_{0} \hat{k} \end{array}$

La trayectoria es una cónica

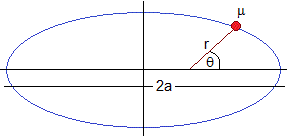
$\begin{array}{l} r = \frac{d}{1 + ε \cos θ} \\ d = \frac{L_{c m}^{2}}{μ G m_{1} m_{2}} = \frac{{(- \frac{m}{2} v_{0} r_{0})}^{2}}{\frac{m}{2} G m^{2}} = \frac{1}{2} \frac{v_{0}^{2} r_{0}^{2}}{G m} \\ ε = \sqrt{1 + \frac{2 L_{c m}^{2} E_{c m}}{μ {(G m_{1} m_{2})}^{2}}} = \sqrt{1 + \frac{2 {(- \frac{m}{2} v_{0} r_{0})}^{2} (\frac{1}{4} m v_{0}^{2} - G \frac{m^{2}}{r_{0}})}{\frac{m}{2} {(G m^{2})}^{2}}} = \frac{1}{G m} | \frac{v_{0}^{2} r_{0}}{2} - G m | = | \frac{v_{0}^{2} r_{0}}{2 G m} - 1 | \end{array}$

El periodo es

$\begin{array}{l} P^{2} = \frac{4 π^{2}}{G (m_{1} + m_{2})} a^{3} \\ P^{2} = \frac{2 π^{2}}{G m} a^{3} \end{array}$

El eje mayor a de la elipse es

$\begin{array}{l} 2 a = \frac{d}{1 + ε} + \frac{d}{1 - ε} \\ a = \frac{d}{1 - ε^{2}} = \frac{\frac{1}{2} \frac{v_{0}^{2} r_{0}^{2}}{G m}}{1 - {(\frac{v_{0}^{2} r_{0}}{2 G m} - 1)}^{2}} = \frac{2 G m r_{0}}{4 G m - v_{0}^{2} r_{0}} \end{array}$

Movimiento de las dos partículas

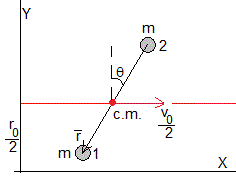
Conocido el movimiento del centro de masas y el movimiento relativo, determinamos la posición de cada una de las partículas

$\begin{array}{l} \vec{R} = \frac{1}{2} v_{0} t \cdot \hat{i} + \frac{r_{0}}{2} \hat{j}, \vec{r} = - r \sin θ \cdot \hat{i} - r \cos θ \cdot \hat{j} \\ \vec{r_{1}} = (\frac{1}{2} v_{0} t - \frac{r}{2} \sin θ) \hat{i} + (\frac{r_{0}}{2} - \frac{r}{2} \cos θ) \hat{j} \\ \vec{r_{2}} = (\frac{1}{2} v_{0} t + \frac{r}{2} \sin θ) \hat{i} + (\frac{r_{0}}{2} + \frac{r}{2} \cos θ) \hat{j} \end{array}$

Escalas

Se definen las escalas de distancias y tiempos

$ρ = \frac{r}{r_{0}}, τ = \frac{\sqrt{G m}}{r_{0}^{3 / 2}} t$

La velocidad inicial (V=ρ/τ) en este sistema de unidades es

$V_{0} = \sqrt{\frac{r_{0}}{G m}} v_{0}$

La ecuación de la trayectoria, dividiendo por r₀

$\begin{array}{l} ρ = \frac{δ}{1 + ε \cos θ} \\ δ = \frac{d}{r_{0}} = \frac{1}{2} V_{0}^{2}, ε = \frac{V_{0}^{2}}{2} - 1 \end{array}$

Para que la trayectoria sea una elipse, ε<1, la velocidad inicial V₀<2

El semieje mayor de la elipse

$α = \frac{a}{r_{0}} = \frac{2}{4 - V_{0}^{2}}$

El periodo

$\begin{array}{l} \frac{{r_{0}}^{3}}{G m} T^{2} = \frac{2 π^{2}}{G m} {(α r_{0})}^{3} \\ T = \sqrt{2} π α^{3 / 2} \end{array}$

La posición inicial relativa de la segunda partícula en el instante τ=0 es, ρ=1. De la ecuación de la trayectoria

$\begin{array}{l} 1 = \frac{\frac{1}{2} V_{0}^{2}}{1 + (\frac{V_{0}^{2}}{2} - 1) \cos θ} \\ \cos θ = 1, θ = 0 \end{array}$

Dividiendo entre r₀, obtenemos la posición de cada una de las partículas en este sistema de unidades

$\begin{array}{l} \vec{ρ_{1}} = (\frac{1}{2} V_{0} τ - \frac{ρ}{2} \sin θ) \hat{i} + (\frac{1}{2} - \frac{ρ}{2} \cos θ) \hat{j} \\ \vec{ρ_{2}} = (\frac{1}{2} V_{0} τ + \frac{ρ}{2} \sin θ) \hat{i} + (\frac{1}{2} + \frac{ρ}{2} \cos θ) \hat{j} \end{array}$

Ecuación de Kepler

Para determinar las posiciones de las partículas 1 y 2, precisamos relacionar el ángulo θ con el tiempo, τ, la denominada ecuación de Kepler, dado el tiempo τ calculamos el ángulo θ.

$\begin{array}{l} E - ε \sin E = 2 π \frac{t}{P} \\ \tan (\frac{θ}{2}) = \sqrt{\frac{1 + ε}{1 - ε}} \tan (\frac{E}{2}) \end{array}$

Dado el tiempo t calculamos el ángulo E, resolviendo la ecuación trascendente. Dado el ángulo E calculamos el ángulo θ. Expresamos la primera ecuación en el nuevo sistema de unidades

$\begin{array}{l} E - ε \sin E = 2 π \frac{τ}{T} \\ E - ε \sin E = τ \sqrt{\frac{2}{α^{3}}} \end{array}$

Representamos las trayectorias de las partículas para V₀=1.5, que cumple V₀<2

function dosCuerpos
    V0=1.5; %velocidad inicial
    d=V0^2/2; %parámetro
    ex=V0^2/2-1; %excentricidad
    a=2/(4-V0^2); %semieje mayor
    tt=linspace(0.05,10,200);
    x1=zeros(1, length(tt));
    y1=zeros(1, length(tt));
    x2=zeros(1, length(tt));
    y2=zeros(1, length(tt));
    i=1;
    for t=tt
        E=ecuacion(t);
        th=2*atan(sqrt((1+ex)/(1-ex))*tan(E/2));
        r=d/(1+ex*cos(th));
        x1(i)=V0*t/2-r*sin(th)/2;
        y1(i)=1/2-r*cos(th)/2;
        x2(i)=V0*t/2+r*sin(th)/2;
        y2(i)=1/2+r*cos(th)/2;
        i=i+1;
    end
    hold on
    plot(x1, y1)
    plot(x2, y2)
    hold off
    xlabel('x')
    ylabel('y')
    legend('1','2','location','best')
    grid on
    title('Trayectorias')

    function x0=ecuacion(t)
        Me=sqrt(2/a^3)*t;
        x0=Me-ex/2; %valor de partida
        while(1)
            x=x0-(x0-ex*sin(x0)-Me)/(1-ex*cos(x0));
            if abs((x-x0)/x0)<1e-6
                break;
            end
            x0=x;
        end
    end
end

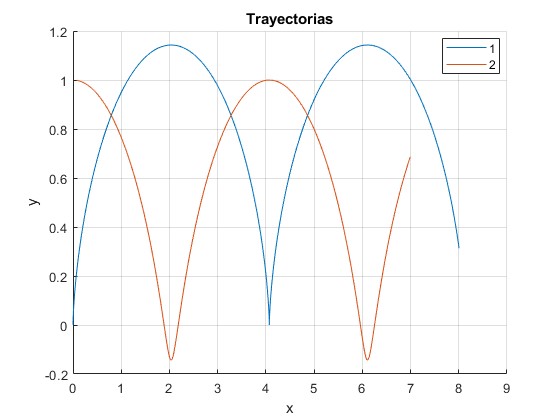
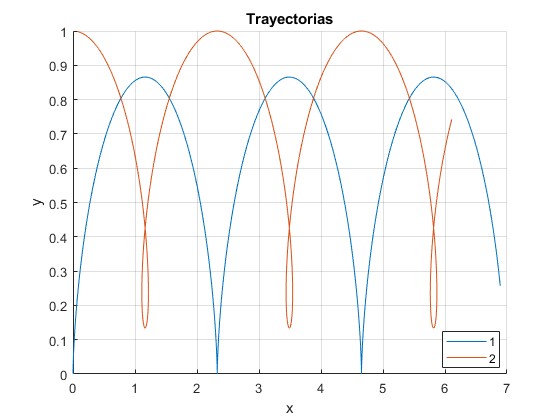
Representamos las trayectorias de las partículas para V₀=1.3

Actividades

Se introduce

La velocidad inicial adimensional V₀<2, en el control titulado Velocidad inicial

Se pulsa el botón titulado Nuevo

Se observan las trayectorias de las dos partículas que forman el sistema aislado. El centro de masas, punto de color negro, se mueve con velocidad constante v₀/2 a lo largo de la recta y=1/2

Velocidad inicial:

Trayectorias

En el sistema de referencia del centro de masas, las posiciones de los cuerpos celestes de masas m₁ y m₂ son

$\begin{array}{l} \vec{r_{1 c m}} = \frac{m_{2}}{m_{1} + m_{2}} \frac{d}{1 + ε \cos θ} \hat{r} \\ \vec{r_{2 c m}} = - \frac{m_{1}}{m_{1} + m_{2}} \frac{d}{1 + ε \cos θ} \hat{r} \end{array}$

Donde θ es la posición angular, el vector unitario indica la dirección de la línea que une ambos cuerpos

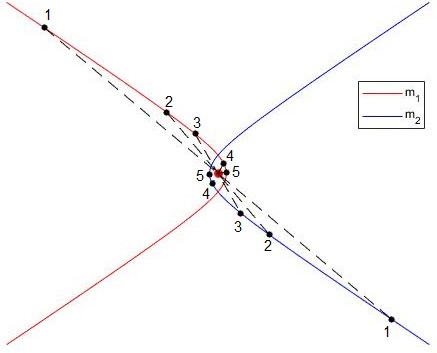
Dibujamos las trayectorias relativas al CM de dos partículas de masas m₁ y m₂, de excentricidad ε, asignamos al parámetro d=1

Trayectorias elípticas, ε<1

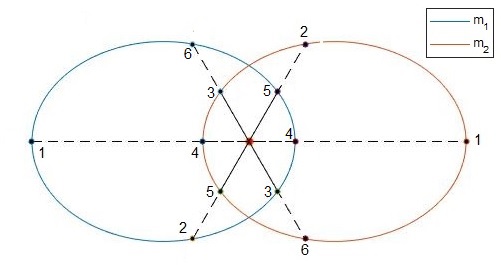
m₁=m₂, ε=0.65

m2=1; %masas
m1=m2;
e=0.65; %excentricidad

%trayectorias en el sistema CM
th=1:360;
radio=1./(1+e*cos(th*pi/180));
x1=radio.*cos(th*pi/180)*m2/(m1+m2);
y1=radio.*sin(th*pi/180)*m2/(m1+m2);
x2=-radio.*cos(th*pi/180)*m1/(m1+m2);
y2=-radio.*sin(th*pi/180)*m1/(m1+m2);
hold on
plot(x1,y1)
plot(x2,y2)
plot(0,0,'o','markersize',6, 'markeredgecolor','r','markerfacecolor','r')

%posiciones
for pos=60:60:360
    line([x1(pos),x2(pos)],[y1(pos),y2(pos)],'lineStyle','--', 'color','k')
    plot(x1(pos),y1(pos),'o','markersize',4, 'markeredgecolor',
'k', 'markerfacecolor','k')
    plot(x2(pos),y2(pos),'o','markersize',4,'markeredgecolor',
'k','markerfacecolor','k')
end
hold off
legend('m_1','m_2')
axis equal
axis off

m₁=2m₂, ε=0.65

Cambiamos la segunda línea de código

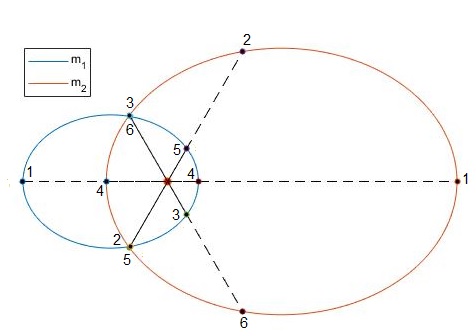
El centro de masas está en el origen y se trazan las trayectorias elípticas de los dos cuerpos y se señalan sus posiciones para un ángulo dado θ. La línea que une ambas posiciones pasa por el c.m. y se cumplirá que m₁r₁=m₂r₂. Como m₁ es el doble que m₂, la distancia del centro de masas al primer cuerpo r₁, será la mitad que r₂

Trayectorias hiperbólicas, ε>1

m₁=m₂, ε=1.2

m2=1; %masas
m1=m2;
e=1.2; %excentricidad

%trayectorias en el sistema CM
th=1:acosd(-1/e)-5;
radio=1./(1+e*cos(th*pi/180));
x1=radio.*cos(th*pi/180)*m2/(m1+m2);
y1=radio.*sin(th*pi/180)*m2/(m1+m2);
x2=-radio.*cos(th*pi/180)*m1/(m1+m2);
y2=-radio.*sin(th*pi/180)*m1/(m1+m2);
hold on
plot(x1,y1,'r')
plot(x2,y2,'b')
plot(x1,-y1,'r')
plot(x2,-y2,'b')
plot(0,0,'o','markersize',6,'markeredgecolor','r','markerfacecolor','r')

%posiciones
for pos=[10, 60,120, 130,140]
    line([x1(pos),x2(pos)],[y1(pos),y2(pos)],'lineStyle','--', 'color','k')
    plot(x1(pos),y1(pos),'o','markersize',4,'markeredgecolor',
'k','markerfacecolor','k')
    plot(x2(pos),y2(pos),'o','markersize',4,'markeredgecolor',
'k','markerfacecolor','k')
end
legend('m_1','m_2', 'location','best')

hold off
axis off
axis equal

Sistema aislado formado por la Tierra y la Luna

Supongamos un sistema aislado formado por la Tierra y la Luna en órbita circular alrededor de su centro de masa. La posición del centro de masas se calculará de acuerdo con la siguiente relación

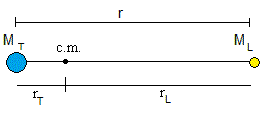
M_Tr_T=M_Lr_L

r=r_T+r_L

La posición del centro de masas está más cerca de la masa mayor.

$r_{T} = \frac{M_{L}}{M_{T} + M_{L}} r$

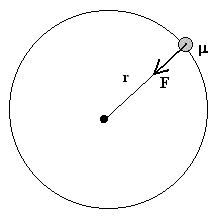
El movimiento de los dos cuerpos celestes es equivalente al movimiento de una partícula de masa reducida μ, bajo la acción de la fuerza F que describe la interacción mutua, la fuerza de atracción entre dos masas separadas una distancia r=r_T+r_M

Si dicha partícula describe un movimiento circular de radio r, su aceleración es ω²·r. La segunda ley de Newton se escribe.

$μ ω^{2} r = G \frac{M_{T} M_{L}}{r^{2}}, ω^{2} = G \frac{M_{T} + M_{L}}{r^{3}}$

El periodo P es

$P^{2} = \frac{4 π^{2} r^{3}}{G (M_{L} + M_{T})}$

Una vez determinado el movimiento relativo, es decir, el radio r que describe la partícula de masa reducida μ, el movimiento de cada una de las partículas es el siguiente:

La Tierra de masa M_T describe un movimiento circular de radio $r_{T} = \frac{M_{L}}{M_{T} + M_{L}} r$ alrededor del c.m de periodo P.
La Luna de masa M_L describe un movimiento circular de radio $r_{L} = \frac{M_{T}}{M_{T} + M_{L}} r$ alrededor del c.m y del mismo periodo.

Cuando la masa de una de las partículas es muy grande comparada con la de la otra, el centro de masas coincide aproximadamente con el centro de la primera partícula. Supondremos que la segunda se mueve alrededor de un centro fijo de fuerzas. Por ejemplo, un satélite artificial que describe una órbita alrededor de la Tierra.

En un sistema formado por dos cuerpos que interaccionan de acuerdo con la ley de la Gravitación Universal, conocido el periodo P y la separación r entre ambos (por ejemplo, un sistema binario de estrellas) se puede calcular a partir de la tercera ley de Kepler, la masa combinada m₁+m₂ de los dos cuerpos.

Representamos las órbitas circulares de la Tierra y de la Luna alrededor del centro de masas, suponiendo que es un sistema aislado. Tomamos el radio de la Tierra como unidad de longitud

Radio de la Tierra, R_T=6.37·10⁶ m
Distancia Tierra-Luna, r=3.84·10⁸ m
Masa de la Tierra, M_T=5.98·10²⁴ kg
Masa de la Luna, M_L=7.34·10²² kg

ML=7.349e22; %masa Luna
MT=5.98e24; %masa Tierra
RT=6.37e6; %radio Tierra
r=384.4e6; %distancia Tierra-Luna
rT=ML*r/(RT*(MT+ML)); %distancia del centro de la Tierra al centro de masas
rL=r/RT-rT; %distancia del centro de la Luna al centro de masas
hold on
t=(1:360)*pi/180;
x1=cos(t);
y1=sin(t);
fill(x1,y1,'c')
fplot(@(t) cos(t), @(t) sin(t),[0,2*pi],'b');
fplot(@(t) rT+rT*cos(t), @(t) rT*sin(t),[0,2*pi])
fplot(@(t) rT+rL*cos(t), @(t) rL*sin(t),[0,2*pi])
plot(rT,0,'ko','markersize',3,'markerfacecolor','k')
plot(0,0,'bo','markersize',3,'markerfacecolor','b')
hold off
grid on
axis equal
% xlim([-1,3]) %para ver la órbita circular de la Tierra
xlabel('x/R_T')
ylabel('y/R_T')
title('Movimiento alrededor del c.m.')

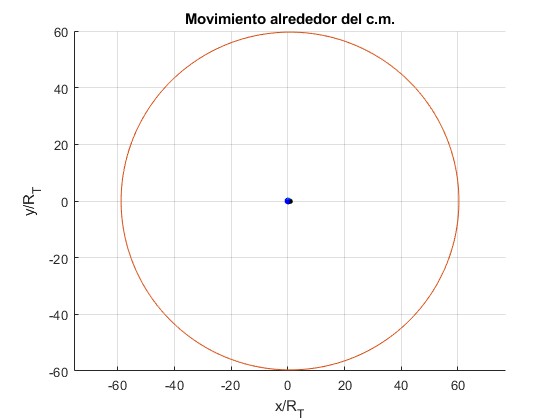
La Luna describe la órbita circular de radio r_L=59.6·R_T alrededor del centro de masas. La órbita circular de la Tierra no se ve a esta escala

Ampliamos la imagen en las proximidades del centro de la Tierra

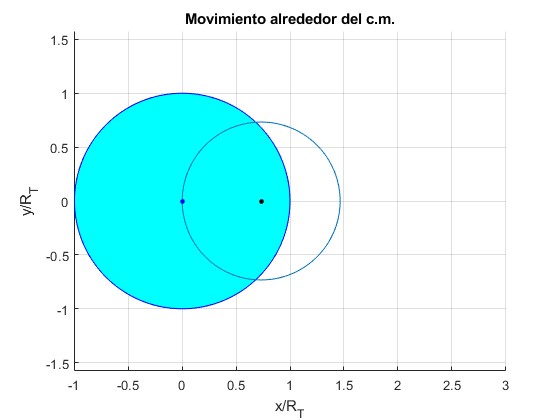
El punto de color negro es el centro de masas que dista r_T=0.7326·R_T del centro de la Tierra. El círculo de color azul claro representa la Tierra de radio unidad. El centro de la Tierra descibe una órbita circular de radio r_T alrededor del centro de masas

Actividades

Se introduce

La relación de masas m₂/m₁ de las estrellas un número comprendido entre 1 y 10 en el control titulado Cociente masas m₂/m₁

Se pulsa el botón Nuevo.

La masa de del cuerpo de color amarillo m₁ es fija, se puede cambiar la masa del cuerpo azul. La distancia entre los dos cuerpos permanece fija e igual a una unidad de longitud. Se ha establecido un sistema de unidades tal que el G·m₁=1. El periodo se calcula entonces, mediante la siguiente fórmula

$P^{2} = \frac{4 π^{2}}{(1 + m_{2} / m_{1})}$

Considerar el caso de que ambos cuerpos tienen la misma masa.

Cociente de masas m₂/m₁

Trayectorias hiperbólicas

Sean dos cuerpos celestes de masas m₁ y m₂ inicialmente muy alejados uno del otro. Supongamos que el cuerpo de masa m₂ está inicialmente en reposo y el cuerpo de masa m₁ se mueve con velocidad v₀. La distancia entre la dirección de la velocidad del segundo cuerpo es b (denominado parámetro de impacto), tal como se muestra en la figura. Este problema es similar a la dispersión de una partícula cargada (partículo alfa) por un núcleo ligero. La fuerza de interacción entre cargas del mismo signo es repulsiva y entre dos cuerpos es atractiva

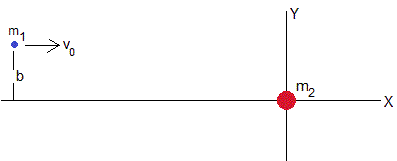
Calculemos los valores de E_cm y L_cm para una partícula proyectil de masa m₁ con velocidad v₀ y parámetro de impacto b, que se lanza contra un blanco inicialmente en reposo.

Los valores de E y L respecto del sistema de referencia fijo en el laboratorio son

$L = m_{1} v_{0} b E = \frac{1}{2} m_{1} v_{0}^{2}$

La posición y la velocidad del centro de masas es

$y_{c m} = \frac{m_{1} b}{m_{1} + m_{2}} v_{c m} = \frac{m_{1} v_{0}}{m_{1} + m_{2}}$

La energía y el momento angular en el S.R. del c.m. son

$\begin{array}{l} \begin{array}{l} E_{c m} = \frac{1}{2} μ v_{0}^{2} \\ L_{c m} = μ v_{0} b \end{array} \\ ε = \sqrt{1 + \frac{2 L_{c m}^{2} E_{c m}}{μ {(G m_{1} m_{2})}^{2}}} = \sqrt{1 + \frac{v_{0}^{4} b^{2}}{G^{2} {(m_{1} + m_{2})}^{2}}} \\ d = \frac{L_{c m}^{2}}{μ (G m_{1} m_{2})} = \frac{v_{0}^{2} b^{2}}{G (m_{1} + m_{2})} \end{array}$

La ecuación de la trayectoria hiperbólica es (véase la justificación al final de la página titulada ' Trayectorias hiperbólicas')

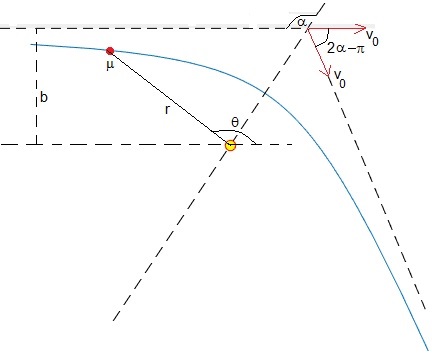
$r = \frac{b p}{1 + \cos θ + p \sin θ} p = \frac{b v_{0}^{2}}{G (m_{1} + m_{2})}$

El cambio en la dirección de la velocidad relativa es 2α-π, donde cos(α)=-1/ε

Movimiento del proyectil y del blanco en el S.R. del c.m.

Conocido r(θ) determinamos la trayectoria del proyectil y del blanco en el SR del c.m. Para ello, basta relacionar $\vec{r}$ (posición del proyectil respecto del blanco) con $\vec{r_{1 c m}}$ (posición del proyectil respecto del c.m.) y con $\vec{r_{2 c m}}$ (posición del blanco respecto del c.m.) tal como hemos hecho al principio de esta página.

$\begin{array}{l} \vec{r_{1 c m}} = \vec{r_{1}} - \vec{r_{c m}} = \frac{m_{2} \vec{r}}{m_{1} + m_{2}} \\ \vec{r_{2 c m}} = \vec{r_{2}} - \vec{r_{c m}} = - \frac{m_{1} \vec{r}}{m_{1} + m_{2}} \end{array}$

Las partículas antes y después de la interacción (cuando se encuentran suficientemente alejadas) tienen el mismo módulo de la velocidad,

$v_{1 c m} = \frac{m_{2}}{m_{1} + m_{2}} v_{0}$

su dirección ha cambiado tal como vemos en el programa interactivo al final de la página

Movimiento del proyectil y del blanco en el S.R. del Laboratorio

En el programa interactivo, vemos la trayectoria seguida por el proyectil (en azul) y por el blanco (en rojo) en el S.R. del Laboratorio, también se señala la posición del c.m mediante una cruz de color negro.

Como estamos estudiando un sistema aislado de dos partículas interactuantes, el centro de masas se mueve con velocidad constante.

$\begin{array}{l} x_{c m} = x_{0 c m} + \frac{m_{1}}{m_{1} + m_{2}} v_{0} \cdot t \\ y_{c m} = \frac{m_{1} b}{m_{1} + m_{2}} \end{array}$

donde x_0cm, es la posición inicial del c.m.

Conocidas la posición del proyectil $\vec{r_{1 c m}}$ y del blanco $\vec{r_{2 c m}}$ respecto del c.m. y la posición $\vec{r_{c m}}$ del centro de masas, determinamos la posición del proyectil $\vec{r_{1}}$ y del blanco $\vec{r_{2}}$ en el S. R. del Laboratorio.

$\begin{array}{l} \vec{r_{1}} = \vec{r_{1 c m}} + \vec{r_{c m}} \\ \vec{r_{2}} = \vec{r_{2 c m}} + \vec{r_{c m}} \end{array}$

Como el proyectil y el blanco forman un sistema aislado, la energía cinética total antes y después del proceso de interacción se conserva.

Variación de la velocidad

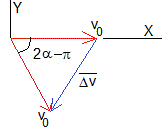
El blanco se encuentra inicialmente en reposo y como resultado de la interacción se mueve. Para que se conserve la energía, el proyectil habrá de experimentar una disminución de su velocidad y energía cinética. Por tanto, como consecuencia del proceso de interacción hay una transferencia de energía del proyectil (partícula 1) al blanco (partícula 2).

La velocidad relativa no cambia de módulo, pero cambia de dirección, la variación de velocidad relativa es

$\begin{array}{l} \vec{Δ v} = (v_{0} \cos (2 α - π) - v_{0}) \hat{i} - v_{0} \sin (2 α - π) \hat{j} \\ {\begin{cases} \cos (2 α - π) = 1 - 2 \cos^{2} α = 1 - \frac{2}{ε^{2}} \\ \sin (2 α - π) = - 2 \sin α \cos α = \frac{2}{ε^{2}} \sqrt{ε^{2} - 1} \end{cases} \\ \vec{Δ v} = - 2 v_{0} {(1 + \frac{v_{0}^{4} b^{2}}{G^{2} {(m_{1} + m_{2})}^{2}})}^{- 1} \hat{i} - \frac{2 v_{0}^{3} b}{G (m_{1} + m_{2})} {(1 + \frac{v_{0}^{4} b^{2}}{G^{2} {(m_{1} + m_{2})}^{2}})}^{- 1} \hat{j} \end{array}$

Calculamos la variación de velocidad de cada una de las partículas

La variación de velocidad relativa es

$\vec{Δ v} = \vec{Δ v_{1}} - \vec{Δ v_{2}}$

En un sistema aislado, el momento lineal se conserva, la velocidad del centro de masa permanece constante

$\begin{array}{l} \vec{V_{c m}} = \frac{m_{1} \vec{v_{1}} + m_{2} \vec{v_{2}}}{m_{1} + m_{2}} \\ m_{1} \vec{Δ v_{1}} + m_{2} \vec{Δ v_{2}} = 0 \end{array}$

Despejamos las variaciones de velocidad de cada una de las partículas

$\begin{array}{l} \vec{Δ v_{1}} = \frac{m_{2}}{m_{1} + m_{2}} \vec{Δ v} \\ \vec{Δ v_{2}} = - \frac{m_{1}}{m_{1} + m_{2}} \vec{Δ v} \end{array}$

Actividades

Se introduce

La energía cinética E de la partícula incidente, en el control titulado Energía.
El parámetro de impacto b, en el control titulado P. impacto
La masa de la partícula incidente m₁ se ha fijado en la unidad
La masa del blanco m₂, en el control titulado Masa blanco.

Se elige entre dos posible opciones:

El observador situado en el centro de masa (S.R. del c.m.)
El observador fijo en el laboratorio (S.R. del Laboratorio)

Se pulsa en el botón titulado Nuevo.

El programa, traza las trayectorias de los dos cuerpos que interaccionan. El programa interactivo compara la velocidad inicial de la partícula con la velocidad final. En ambos casos se supone que las partículas están suficientemente alejadas para considerar que su interacción mutua es despreciable.

Observamos que en el S.R. de c.m. el proceso de interacción no cambia el módulo de la velocidad, aunque si cambia su dirección.

En el S.R. del laboratorio, la velocidad final del proyectil es menor que la inicial y el blanco incrementa su velocidad debido a la interacción. Por tanto, en este S.R. hay un cambio tanto en el módulo como en la dirección de la velocidad de la partícula incidente.

Energía: P. impacto:
Masa blanco:

Referencias

C. Antón, J. L. Brun. Gravitational pocket billiards with Mathematica. Revista Mexicana de Física 55 (2) 168–175. Diciembre 2009

O. L. de Lange, J. Pierrus. Solved Problems in Classical Mechanics. Analytical and numerical solutions with comments. Oxford University Press (2010). Question 10.7, pp. 293-296