Dinámica del movimiento circular
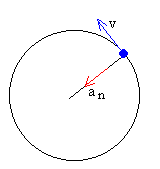
En el estudio del movimiento circular uniforme, hemos visto que la velocidad del móvil no cambia de módulo pero cambia constantemente de dirección. El móvil tiene una aceleración que está dirigida hacia el centro de la trayectoria, denominada aceleración normal y cuyo módulo es
F=m·an
En el programa interactivo, más abajo, simulamos una práctica de laboratorio que consiste en medir con ayuda de un dinamómetro la tensión de la cuerda que sujeta a un móvil que describe una trayectoria circular.
El dinamómetro está situado en el eje de una plataforma móvil y su extremo está enganchado a un móvil que gira sobre la plataforma.
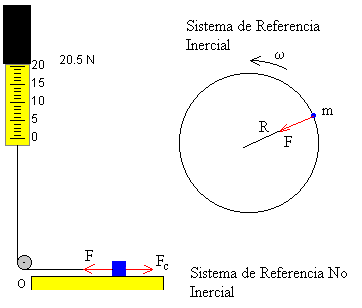
Sistema de Referencia Inercial
Desde el punto de vista de un observador inercial, el móvil describe un movimiento circular uniforme. El móvil cambia constantemente la dirección de la velocidad, aunque su módulo permanece constante. La fuerza necesaria para producir la aceleración normal es
F=mω2R
Esta será la fuerza que mide el dinamómetro tal como vemos en la parte derecha de la figura.
Sistema de Referencia No Inercial
Desde el punto de vista del observador no inercial situado en el móvil, éste está en equilibrio bajo la acción de dos fuerzas. La tensión de la cuerda F y la fuerza centrífuga Fc. La fuerza centrífuga es el producto de la masa por la aceleración centrífuga.
Fc=mω2R
La fuerza centrífuga, no describe ninguna interacción entre cuerpos, como la tensión de una cuerda, el peso, la fuerza de rozamiento, etc. La fuerza centrífuga surge al analizar el movimiento de un cuerpo desde un Sistema de Referencia No Inercial (acelerado) que describe un movimiento circular uniforme.
Actividades
Se introduce
- El radio R de la trayectoria circular (cm), en el control titulado Radio
- La masa de la partícula (g), en el control titulado Masa
- La velocidad angular de rotación (rad/s), en el control titulado V. angular
Se pulsa el botón titulado Nuevo.
Observamos el movimiento del cuerpo. Una flecha sobre la partícula señala la fuerza radial que es necesario ejercer para que describa una trayectoria circular. El sentido de la fuerza está dirigido hacia el centro de la trayectoria.
Manteniendo fijos el radio R y la masa de la partícula m y cambiamos el valor de la velocidad angular de rotación ω.
Práctica de laboratorio
En el laboratorio disponemos de dos dispositivos, uno de PHYWE y otro de PASCO para medir la fuerza F necesaria para que un cuerpo de masa m describa un movimiento circular de radio R con velocidad angular ω o periodo P=2π/ω

El dispositivo de PHYWE se muestra en el fotografía, la plataforma sobre la que se mueve un carrito en la dirección radial, gira accionada por un motor de velocidad angular variable. El carrito tiene una masa de 100 g y se le puede añadir pesas de 50 g. El dinamómetro nos proporciona la medida de la fuerza F, con un cronómetro medimos el periodo P o tiempo que tarda en dar una vuelta y con la regla fijada a la plataforma que gira, medimos el radio R de la circunferencia que describe
Los datos para una masa m=100 g, han sido los siguientes
| Radio R(m) | Periodo P(s) | F(N) medida | F(N) calculada |
|---|---|---|---|
| 0.24 | 1.89 | 0.3 | 0.27 |
| 0.265 | 1.10 | 0.9 | 0.86 |
La fuerza F medida con el dinamómetro y la calculada mediante la fórmula se aproximan.

El dispositivo de PASCO es similar. Una regla de aluminio gira accionada por un motor de velocidad angular variable. La regla permite situar dos masas m iguales a una distancia R del eje. Una de ellas conectada con sensor de fuerza mediante un hilo puede deslizar sobre la regla, la otra fijada mediante tornillos actúa de contrapeso
El radio se ha fijado en R=16 cm. En la primera experiencia, se ha colocado una pesa de 50 g sobre el soporte deslizante de 50.6 g masa y otros 50 g en el contrapeso, lo que hace una masa m=101.6 g, en la segunda experiencia, se ha añadido otra pesa de 50 g. Los resultados han sido los siguientes:
| Masa m(kg) | Periodo P(s) | F(N) medida | F(N) calculada |
|---|---|---|---|
| 0.1016 | 1.3 | 0.3 | 0.38 |
| 0.1516 | 0.75 | 1.9 | 1.7 |
Medida de la aceleración de la gravedad
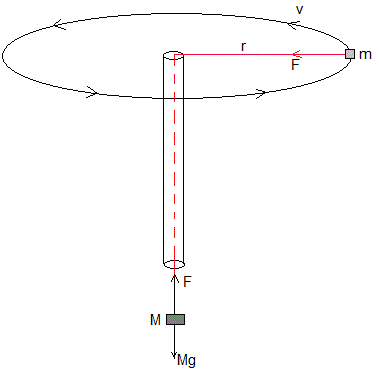
PASCO dispone del equipo de laboratorio ME_9837A, Discover Centripetal Force Kit con el que se puede medir la aceleración de la gravedad con poca precisión.
Se compone de un tubo de plástico hueco por el que se pasa una cuerda en cuyos extremos de colocan masas m y M. Se hace girar la masa m en una circunferencia horizontal de radio r, tal como se muestra en la figura.
Se mide el tiempo t que tarda la masa m en describir n (2 ó 3) vueltas. Se determina su velocidad v
La fuerza F necesaria para que describa el movimiento circular es
La masa M está en equilibrio bajo la acción de dos fuerzas:
- la tensión de la cuerda, F
- el peso, Mg
La mayor fuente de error es la medida del radio r de la trayectoria circular. Se detiene el movimiento circular presionando la cuerda con la mano en el extremo superior del tubo, con una cinta métrica se mide su distancia a la masa m
Referencias
Francis Wunderlich. Determination of "g" through Circular Motion. Am. J. Phys. 34 (12) December 1996, pp. 1199

