Analogía con las series de desintegración radioactiva
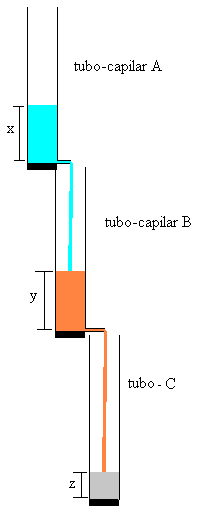
Las ecuaciones que describen la variación de las respectivas columnas de fluido en función del tiempo son las siguientes: (véase las dos páginas anteriores: descarga de un tubo-capilar y carga y descarga de un tubo-capilar).
Velocidades de variación de la altura de columna de fluido en los tres tubos:
- Tubo-capilar A. Si su constante es a, la altura x de la columna de fluido disminuye a razón de ax
- Tubo capilar B. Si su constante es b, la altura y de la columna de fluido disminuye a razón de by y aumenta a razón de ax.
- Tubo C. La altura z de su columna de fluido aumenta a razón de by.
donde x, y y z son las alturas de las columnas de fluido en los tubos A, B y C.
a y b son las constantes de los tubos-capilares A y B.
Las soluciones del sistema del sistema de tres ecuaciones diferenciales de primer orden con las condiciones iniciales t=0, x=x0, y=0, z=0 son las siguientes:
>> syms x y z t a b x0;
>> x=dsolve('Dx=-a*x','x(0)=x0')
x =x0*exp(-a*t)
>> y=dsolve('Dy=a*x0*exp(-a*t)-b*y','y(0)=0');
>> y=simplify(y)
y =(a*x0*exp(-b*t))/(a - b) - (a*x0*exp(-a*t))/(a - b)
>> z=dsolve('Dz=b*((a*x0*exp(-b*t))/(a - b) - (a*x0*exp(-a*t))/(a - b))'
,'z(0)=0')
z =x0 - (a*x0*exp(-b*t) - b*x0*exp(-a*t))/(a - b)
>> x=subs(x,{x0,a},{50,0.0391/2});
>> y=subs(y,{x0,a,b},{50,0.0391/2,0.0391/10});
>> z=subs(z,{x0,a,b},{50,0.0391/2,0.0391/10})
>> hold on
>> ezplot(x,[0,500])
>> ezplot(y,[0,500])
>> ezplot(z,[0,500])
>> hold off
>> xlabel('t(s)')
>> ylabel('h(cm)')
>> title('Serie de desintegración radioactiva')
>> grid on
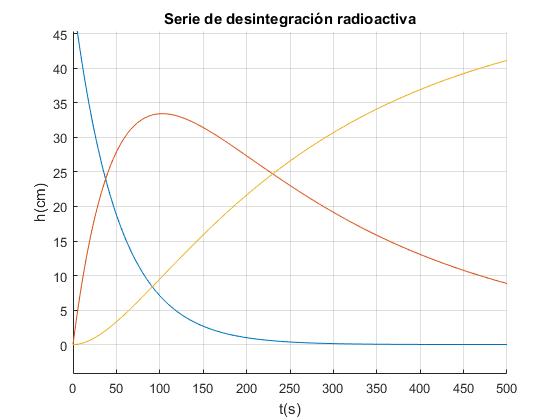
Los datos de las constantes a=0.0391/2, b=0.0391/10 y de x0=50 se han tomado del ejemplo que se describe más abajo
Cuando a=b
y=dsolve('Dy=a*x0*exp(-a*t)-a*y','y(0)=0')
y =a*t*x0*exp(-a*t)
>> z=dsolve('Dz=a*a*t*x0*exp(-a*t)','z(0)=0')
z =x0 - x0*exp(-a*t)*(a*t + 1)
Observamos que el tubo A disminuye su altura x exponencialmente y el tubo C por ser cerrado incrementa siempre su altura. Sin embargo, es más importante el comportamiento del tubo-capilar intermedio B: primero crece la altura de su columna de fluido hasta llegar a un máximo y luego, decrece hasta hacerse cero (en un tiempo teóricamente infinito). Observamos tres fases en el comportamiento del tubo-capilar B:
- Gana en la unidad de tiempo más fluido del que pierde por el capilar (dy/dt>0)
- El máximo indica una situación de equilibrio dinámico, entra tanto fluido en la unidad de tiempo como sale (dy/dt=0).
- Pierde en la unidad de tiempo más fluido que el que aporta el tubo-capilar A (dy/dt<0).
La representación gráfica de x, y y z en función del tiempo, nos permite comprender mejor que:
- Existan materiales radioactivos de tan pequeña vida media como el Radio, 1600 años frente a la edad de la Tierra 2500 millones de años.
- La cantidad de estas sustancias es casi invariable
- La cantidad de plomo se incrementa continuamente.
Evidentemente, por muy grande que fuese la cantidad inicial de Radio en el momento de la formación de la Tierra, al desintegrase, con un periodo de desintegración tan pequeño comparado con la edad de la Tierra, la cantidad existente actualmente sería despreciable. Su presencia se debe a que forma parte de un producto intermedio de una serie radioactiva.
Uranio (238)→ Torio(234) → Protactinio(234) → Uranio(234) → Torio(230) → Radio(226) → ..... Plomo(206)
La existencia de Uranio en cantidades importantes y su elevada vida media 4.56 109 años hace que podamos encontrar Radio como resultado de su desintegración. La baja vida media de los productos intermedios explica la invariabilidad en la proporción de dichos elementos ya que estamos en una situación estacionaria.
En nuestra serie A→ B→ C, en el estado estacionario, dy/dt=0, por lo que ax=by. Podemos calcular la cantidad de sustancia radioactiva y conociendo x y sus respectivas vidas medias.
Si a es pequeño (vida media grande) x disminuye lentamente, la situación de equilibrio dura bastante tiempo. En todos los casos, la sustancia estable C crece continuamente.
Caso particular
Cuando la constante del tubo-capilar A es igual a la constante del tubo-capilar B, a=b. Observamos en la representación gráfica de las respectivas alturas x (en azul) e y (en rojo) de las columnas de fluido,
x=x0·exp(-a·t)
y=x0·a·t·exp(-a·t)
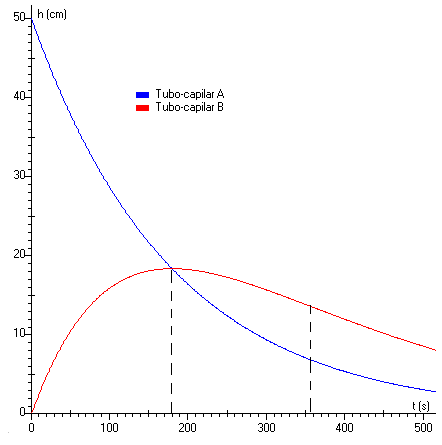
La intersección de ambas curvas se produce en el máximo de la segunda curva
- Intersección
- Máximo, se calcula igualando la derivada primera a cero.
- Punto de inflexión
x=y, t=1/a
El punto de inflexión de la curva y(t), se calcula igualando la derivada segunda a cero
La abscisa del punto de inflexión se encuentra a doble distancia del origen que el máximo.
Ejemplo
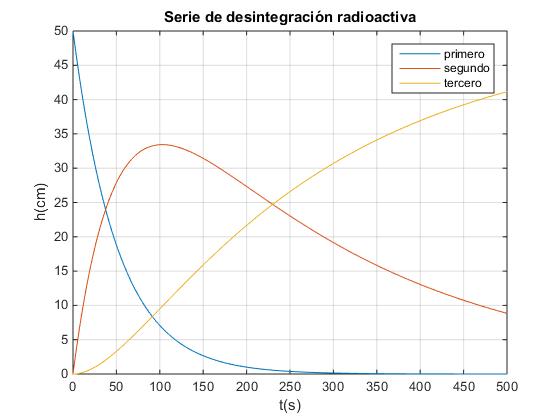
Se introduce un valor grande (10 cm) para la longitud del capilar del tubo A y pequeña (2 cm) para el capilar del tubo B. Se observa la evolución de las alturas de las respectivas columnas de fluido.
Se intercambian los valores, un valor pequeño (2 cm) para la longitud del capilar del tubo A y un valor grande (10 cm) para la longitud del capilar del tubo B. Se observa la evolución de las alturas de las respectivas columnas de fluido.
Se introduce valores iguales, para las longitudes (5 cm) de ambos capilares.
longitud1=2; %la longitud del capilar en cm
longitud2=10;
%constantes de los tubos-capilar
a=0.0391/longitud1;
b=0.0391/longitud2;
h0=50; %altura incial en cm
t=linspace(0,500,500);
h=h0*exp(-a*t); %altura del fluido en el primer tubo-capilar
if a~=b
%altura del fluido en el segundo tubo-capilar
h1=a*h0*(exp(-a*t)-exp(-b*t))/(b-a);
%altura del fluido en el tercer tubo-capilar
h2=h0*(-b*exp(-a*t)+a*exp(-b*t)+b-a)/(b-a);
else
h1=h0*a*t.*exp(-a*t);
h2=h0*(-(a*t+1).*exp(-a*t)+1);
end
plot(t,h,t,h1,t,h2)
grid on
legend('primero','segundo','tercero');
xlabel('t(s)')
ylabel('h(cm)')
title('Serie de desintegración radioactiva')
Experiencia de laboratorio
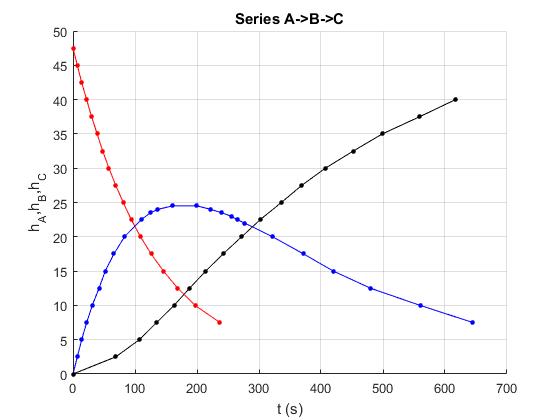
Las medidas tomadas en el laboratorio de las alturas h de aceite en el tubo-capilar A, en el B, y en el tubo C, en función del tiempo t han sido las siguientes
| tA | hA | tB | hB | tC | hC |
|---|---|---|---|---|---|
| 0 | 47.5 | 0 | 0 | 0 | 0 |
| 7 | 45 | 7 | 2.5 | 69 | 2.5 |
| 14 | 42.5 | 14 | 5 | 107 | 5 |
| 22 | 40 | 22 | 7.5 | 135 | 7.5 |
| 30 | 37.5 | 31 | 10 | 163 | 10 |
| 39 | 35 | 42 | 12.5 | 188 | 12.5 |
| 48 | 32.5 | 52 | 15 | 214 | 15 |
| 58 | 30 | 66 | 17.5 | 242 | 17.5 |
| 69 | 27.5 | 83 | 20 | 272 | 20 |
| 81 | 25 | 110 | 22.5 | 302 | 22.5 |
| 94 | 22.5 | 125 | 23.5 | 336 | 25 |
| 109 | 20 | 137 | 24 | 369 | 27.5 |
| 126 | 17.5 | 160 | 24.5 | 407 | 30 |
| 146 | 15 | 200 | 24.5 | 452 | 32.5 |
| 169 | 12.5 | 222 | 24 | 499 | 35 |
| 197 | 10 | 240 | 23.5 | 559 | 37.5 |
| 237 | 7.5 | 255 | 23 | 617 | 40 |
| 265 | 22.5 | ||||
| 277 | 22 | ||||
| 322 | 20 | ||||
| 372 | 17.5 | ||||
| 420 | 15 | ||||
| 480 | 12.5 | ||||
| 560 | 10 | ||||
| 645 | 7.5 |
tA=[0,7,14,22,30,39,48,58,69,81,94,109,126,146,169,197,237];
hA=47.5:-2.5:7.5;
tB=[0,7,14,22,31,42,52,66,83,110,125,137,160,200,222,240,255,265,
277,322,372,420,480,560,645];
hB=[0:2.5:22.5, 23.5,24,24.5,24.5,24,23.5,23,22.5,22,20:-2.5:7.5];
tC=[0,69,107,135,163,188,214,242,272,302,336,369,407,452,499,559,617];
hC=0:2.5:40;
hold on
plot(tA,hA,'-ro','markersize',3,'markerfacecolor','r')
plot(tB,hB,'-bo','markersize',3,'markerfacecolor','b')
plot(tC,hC,'-ko','markersize',3,'markerfacecolor','k')
hold off
grid on
xlabel('t (s)')
ylabel('h_A,h_B,h_C')
title('Series A->B->C')
Referencias
Franco A. Analogías Físicas (Mecánica, Electricidad, Fluidos) . Documentación E.I. (Enseñanzas Integradas). Vol 6 (3),1982, págs. 63-69
Seobie J. Scott R. D., Steward J. F., Use of point of inflection on a radiactive decay curve. Am. J. Phys. 43 (11) November 1975, pp. 1012-1013

