El tubo-capilar

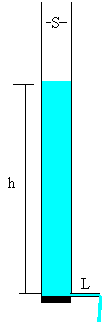
Partimos de la ley de Poiseuille

$G = \frac{π}{8} \frac{(p_{1} - p_{2}) R^{4}}{η L}$

la diferencia de presión p₁-p₂ entre los extremos del capilar es igual a la presión que ejerce la altura h de la columna de fluido de densidad ρ. Luego, p₁-p₂=ρgh

Si G es el volumen de fluido que sale del capilar en la unidad de tiempo, la altura h de la columna de fluido disminuye, de modo que

$- S \frac{d h}{d t} = \frac{π}{8} \frac{ρ g h R^{4}}{η L}$

Siendo S la sección del tubo. Escribimos la ecuación anterior

$\frac{d h}{d t} = - λ h λ = \frac{π}{8} \frac{R^{4} ρ g}{η L S}$

donde λ se denomina constante del tubo-capilar.

Integrado la ecuación diferencial, con la condición inicial de que en el instante t=0, la altura inicial sea h=h₀.

$\int_{h_{0}}^{h} \frac{d h}{h} = - λ \int_{0}^{t} d t h = h_{0} \exp (- λ t)$

La altura de la columna de fluido h decrece exponencialmente con el tiempo t.

Tomando logaritmos neperianos

lnh=lnh₀-λt

Si realizamos la representación gráfica de lnh frente a t obtenemos una línea recta de pendiente –λ.

En el laboratorio de la Escuela de Ingeniería de Eibar (véase el primer artículo citado en las referencias) se ha realizado las siguientes medidas de la altura h de fluido en función del tiempo t con un tubo-capilar usando aceite de automóvil.

h (cm)	t₁ (s)	t₂ (s)
47.5	0	0
45	14	7
42.5	29	14
40	45	22
37.5	62	30
35	81	39
32.5	101	48
30	122	58
27.5	145	69
25	170	81
22.5	197	94
20	232	109
17.5	265	126
15	307	146
12.5	355	169
10	417	197
7.5	500	237
5	610	288

t1=[0,14,29,45,62,81,101,122,145,170,197,232,265,307,355,417,500,610];
t2=[0,7,14,22,30,39,48,58,69,81,94,109,126,146,169,197,237,288];
h=47.5:-2.5:5;
hold on
plot(t1,h,'-ro','markersize',3,'markerfacecolor','r')
plot(t2,h,'-bo','markersize',3,'markerfacecolor','b')
hold off
ylim([0,48])
grid on
xlabel('t (s)')
ylabel('h (cm')
title('Tubo-capilar')

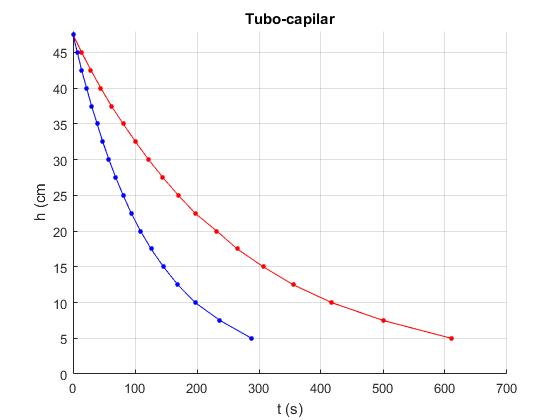
Calculamos la constante de uno de los dos tubos-capilares

t1=[0,14,29,45,62,81,101,122,145,170,197,232,265,307,355,417,500,610];
h=47.5:-2.5:5;
plot(t1,log(h),'ro','markersize',3,'markerfacecolor','r')
grid on
xlabel('t (s)')
ylabel('log(h)')
title('Tubo-capilar')

Aparece la ventana gráfica. En el menú seleccionamos Tools/Basic Fitting, aparece un cuadro de diálogo donde marcamos la casilla linear en Plot fits. A continuación, pulsamos la flecha hacia la derecha --> para mostrar los coeficientes p1 y p2 del polinomio (recta) y=p1*x+p2 de ajuste.

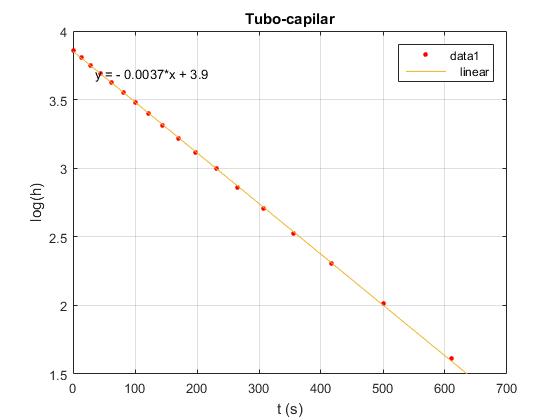
Si introducimos los datos t, y ln(h) obtenemos una línea recta de pendiente -0.0037, de modo que la constante λ=0.0037 s^-1.

Si disponemos de los datos relativos a

Longitud del capilar L y su radio R
Área de la sección del tubo S
Densidad del fluido ρ

Despejamos la viscosidad η del fluido de la fórmula que nos relaciona valor de la constante λ del tubo-capilar, con dichos parámetros, deducida al principio de este apartado.

Vida media

La vida media de unas sustancia radioactiva se define como el tiempo τ necesario para que el número de núcleos activos se reduzca a la mitad.

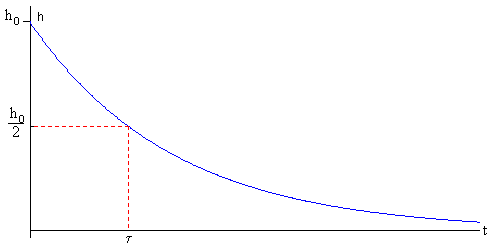
Relacionamos la vida media τ del tubo-capilar y su constante λ , poniendo h=h₀/2.

$\frac{h_{0}}{2} = h_{0} exp(- λ τ) τ = \frac{\ln 2}{λ}$

Fenómenos físicos análogos

La ecuación que describe la descarga de un tubo-capilar es similar a la descarga de un condensador a través de una resistencia y a la desintegración radioactiva.

Las variables físicas análogas se recogen en el siguiente cuadro

Fluidos	Electricidad	Radioactividad
h, altura de la columna de fluido	q, carga del condensador	N, número de núcleos sin desintegrar
dh/dt, velocidad de decrecimiento	i=dq/dt, intensidad de la corriente eléctrica	dN/dt, actividad radioactiva en valor absoluto
λ , constante del tubo-capilar	1/RC, constante del circuito	λ , constante de desintegración

Actividades

Se introduce

la longitud del tubo-capilar en cm, en el control titulado Longitud capilar.
La altura inicial h₀ de la columna de fluido se fija en 50 cm.

Se pulsa el botón titulado Nuevo.

Comienza a salir el fluido por el capilar. Simultáneamente, se traza la curva que nos describe la altura de fluido en función del tiempo. Observamos que es una función exponencial decreciente. Se marca el tiempo que tarda en alcanzarse la mitad de la altura inicial, lo que se conoce como vida media.

Longitud capilar:

Otros tubos capilares

El aceite de automóvil tiene alta viscosidad, por lo que la longitud del capilar puede ser reducida (menor que 15 cm). Sin embargo, la utilización de aceite en un laboratorio escolar puede ser un inconveniente cuando las medidas las realizan los estudiantes.

Depósito de agua de sección constante

El agua tiene una baja viscosidad, por lo que el capilar tiene que tener bastante longitud, para asegurarse que el agua fluye en régimen laminar. En el segundo artículo citado en las referencias, se proporcionan los datos de un tubo-capilar que utiliza agua como fluido.

Longitud del tubo 122 cm (4 ft)
Diámetro interno 1.67 cm (21/32 in)
Longitud del capilar 122 cm (4 ft)
Diámetro interno de 1.25 a 1.75 mm

Depósito de agua de sección variable

Se puede evitar el largo capilar, construyendo un depósito de sección variable, una de cuyas paredes no es vertical, sino de forma que su sección disminuye con la altura, tal como se muestra en la figura.

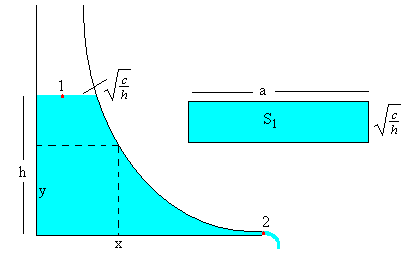
Vamos a mostrar que cuando la forma de la parte curva del depósito es y=c/x²

donde c es constante, la variación de la altura h del agua del depósito disminuye exponencialmente con el tiempo t.

Elegimos dos puntos del fluido, el 1 en la superficie libre, la sección del depósito es S₁ y la velocidad del fluido en dicha sección es v₁. El punto 2 está en el extremo del capilar de pequeña sección S₂, la velocidad del fluido a la salida del depósito es v₂.

La ecuación de continuidad se escribe

v₁S₁=v₂S₂

y la ecuación de Bernoulli

$p_{1} + ρ g y_{1} + \frac{1}{2} ρ v_{1}^{2} = p_{2} + ρ g y_{2} + \frac{1}{2} ρ v_{2}^{2}$

Por otra parte, el elemento de fluido delimitado por las secciones S₁ y S₂ está en contacto con el aire a la misma presión. Luego, p₁=p₂=p₀.

La diferencia de alturas es y₁-y₂=h. Siendo h la altura de la columna de fluido

De estas dos ecuaciones obtenemos v₁ y v₂

$v_{2} = S_{1} \sqrt{\frac{2 g h}{S_{1}^{2} - S_{2}^{2}}}$

Si S₁>>S₂ obtenemos

$v_{2} = \sqrt{2 g h}$

El volumen de fluido que sale del depósito en la unidad de tiempo es S₂v₂, y en el tiempo dt será S₂v₂dt . Como consecuencia disminuirá la altura h del depósito

-S₁dh= S₂v₂dt

La sección rectangular variable S₁ es el producto del lado a de longitud constante y del lado de longitud variable.

$S_{1} = a \sqrt{\frac{c}{h}}$

donde c es una constante. La variación de la altura h del fluido en el depósito con el tiempo t se escribe

$\begin{array}{l} - a \sqrt{\frac{c}{h}} d h = S_{2} \sqrt{2 g h} \cdot d t \\ \frac{d h}{h} = - λ \cdot d t \end{array}$

donde λ se denomina constante del tubo-capilar.

Integrado la ecuación diferencial, con la condición inicial de que en el instante t=0, la altura inicial sea h=h₀.

h=h₀·exp(-λt)

En el tercer artículo citado en las referencias se dan detalles del depósito empleando. Las dimensiones de las partes rectas es de 25.4 cm (10 in)

La parte curva tiene la forma y=819.1/x² cm, de modo que cuando x=25.4 cm (10 in) y=1.27 cm (0.5 in). El depósito no se extiende obviamente, hasta el infinito sino que se corta a esta distancia 25.4 cm. Por tanto, la altura del fluido en función del tiempo, no proporciona buenos resultados cuando h es inferior a 1.27 cm.

Referencias

Franco A. Analogías Físicas (Mecánica, Electricidad, Fluidos) . Documentación E.I. (Enseñanzas Integradas). Vol 6 (3), 1982, págs. 63-69

I A Sianoudis, E Drakaki An approach to Poiseuille's law in an undergraduate laboratory experiment. Eur. J. Phys. 29 (2008) pp. 489-495

J.LLoyd Bohn, Francis H. Nadig, Hydrodynamic Model for Demonstrations in Radioactivity. Am. J. Phys. (1938), pp. 320-323

Smithson J. R., Pinkston E. R., Half-life of a water column as a laboratory exercise in exponential decay. Am. J. Phys. 28 (1960) pp. 740-742.