Carga y descarga de un tubo-capilar
El frasco de Mariotte
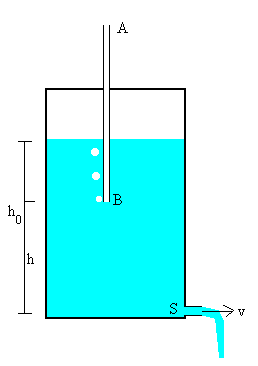
De acuerdo con el teorema de Torricelli, la velocidad de salida de un líquido por un orificio practicado en su fondo es la misma que la que adquiere un cuerpo que cayese libremente en el vacío desde una altura h, siendo h la altura de la columna de fluido
A medida que el fluido sale por el orificio, la altura h de fluido en el depósito va disminuyendo. Si S es la sección del orificio, el gasto Sv, o volumen de fluido que sale por el orificio en la unidad de tiempo no es constante. Si queremos producir un gasto constante, utilizamos el denominado frasco de Mariotte.
Consiste en un frasco lleno de fluido hasta una altura h0, que está cerrado por un tapón atravesado por un tubo cuyo extremo inferior está sumergido en el líquido. El fluido sale del frasco por un orificio practicado en el fondo del recipiente. En el extremo inferior B del tubo, la presión es la atmosférica ya que está entrando aire por el tubo, a medida que sale el líquido por el orificio.
La velocidad de salida del fluido no corresponderá a la altura h0 desde el orificio a la superficie libre de fluido en el frasco, sino a la altura h o distancia entre el extremo inferior B del tubo y el orificio.
Dado que h permanece constante en tanto que el nivel de líquido esté por encima del extremo inferior del tubo, la velocidad del fluido y por tanto, el gasto se mantendrán constantes. Cuando la altura de fluido en el frasco h0 es menor que h, la velocidad de salida v del fluido deja de ser constante
La velocidad de salida v puede modificarse subiendo o bajando el extremo inferior del tubo AB en el frasco.
Carga y descarga de un tubo-capilar
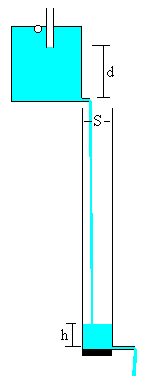
La distancia d entre el extremo inferior del tubo y el orificio inferior en el fraco de Mariotte regula el gasto.
Entra fluido en el tubo-capilar proveniente del frasco de Mariotte y sale a través del capilar.
Sea G el gasto del frasco de Mariotte, entonces, Z=G/S es la velocidad con que se incrementa la altura de fluido en el tubo-capilar, siendo S la sección del tubo. Por otra parte, la velocidad con que disminuye la altura de fluido es -λ h debido a que el fluido sale por el capilar.
La variación de la altura h de la columna de fluido vendrá dada por la siguiente ecuación.
Integrando esta ecuación con la condición inicial de que h=0, en el instante t=0, obtenemos
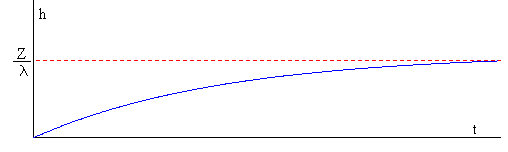
La altura crece hasta alcanzar un valor máximo constante hmáx=Z/λ cuando . Cuando se ha alcanzado la máxima altura constante, (dh/dt=0) la cantidad de fluido que entra en el tubo aportada por el frasco de Mariotte es igual a la que sale por el capilar.
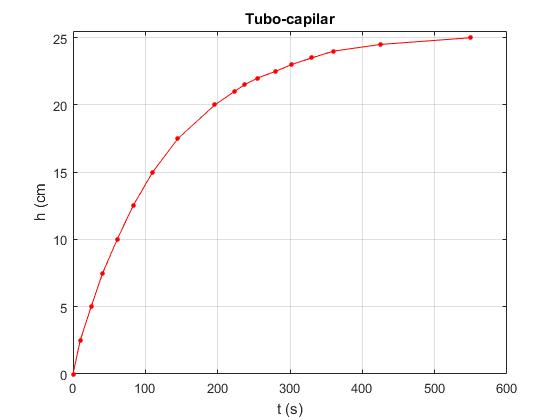
Se han tomado las siguientes medidas de la altura h de aceite en el tubo capilar en función del tiempo t
x=[0,10,25,41,61,83,110,145,196,223,237,255,280,302,330,360,425,550];
y=[0:2.5:20,21:0.5:25];
plot(x,y,'-ro','markersize',3,'markerfacecolor','r')
ylim([0,25.5])
grid on
xlabel('t (s)')
ylabel('h (cm')
title('Tubo-capilar')
| h (cm) | t (s) |
|---|---|
| 0 | 0 |
| 2.5 | 10 |
| 5 | 25 |
| 7.5 | 41 |
| 10 | 61 |
| 12.5 | 83 |
| 15 | 110 |
| 17.5 | 145 |
| 20 | 196 |
| 21 | 223 |
| 21.5 | 237 |
| 22 | 255 |
| 22.5 | 280 |
| 23 | 302 |
| 23.5 | 330 |
| 24 | 360 |
| 24.5 | 425 |
| 25 | 550 |
Fenómenos físicos análogos
2.-Proceso de desintegración radioactiva cuando las partículas que se desintegran se producen a razón constante.
Para producir núcleos de una sustancia radioactiva se coloca una muestra de una sustancia dada en el interior de un reactor nuclear. Los núcleos radioactivos se producen como consecuencia de la captura de un neutrón por los núcleos de dicha sustancia. Por ejemplo, cuando bombardeamos 59Co con neutrones, obtenemos 60Co que es radioactivo b con una vida media de 5.27 años. Otro método para obtener núcleos radioactivos, consiste en bombardear la sustancia con partículas cargadas, tales como protones o deuterones, usando aceleradores de partículas. En ambos casos, los núcleos radioactivos se producen a razón de Z núcleos por segundo.
Variables físicas análogas
| Fluidos | Electricidad | Radioactividad |
|---|---|---|
| Z, altura/unidad de tiempo, incremento de al altura de la columna de fluido aportado por el frasco de Mariotte | Vε/R, carga/unidad de tiempo o intensidad de la corriente aportada por la pila | Z, nº de partículas/ unidad de tiempo producidas por el reactor |
| -λ h, altura/unidad de tiempo, que disminuye la columna de fluido, al salir por el capilar | -q/RC, carga/unidad de tiempo que sale del condensador | -λN, nº de partículas que se desintegran en la unidad de tiempo |
| Z/λ, máxima altura que alcanza el fluido en el tubo. | VεC, carga máxima del condensador | Z/λ, nº máximo de partículas radioactivas. |
Actividades
Se introduce
La longitud del tubo-capilar en cm, en el control titulado Longitud capilar.
Se regula la distancia entre el extremo inferior del tubo y el orificio de salida del frasco de Mariotte, en el control titulado Altura del tubo. Cuanto mayor sea la distancia mayor es la cantidad de fluido que sale en la unidad de tiempo.
Se pulsa el botón titulado Nuevo.
A medida que sale fluido por el orificio practicado en el fondo del frasco de Mariotte, su altura disminuye. Cuando queda al descubierto el extremo inferior del tubo, la velocidad de salida del fluido deja de ser constante, el llenado del tubo-capilar se interrumpe.
En la parte derecha, se representa la altura de la columna de fluido en función del tiempo. Al cabo de un cierto tiempo (teóricamente infinito) se alcanza la altura máxima, el volumen de fluido por unidad de tiempo aportado por el frasco de Mariotte es igual al volumen de fluido por unidad de tiempo que sale por el capilar, estamos en el estado estacionario.
Referencias
Franco A. Analogías Físicas (Mecánica, Electricidad, Fluidos) . Documentación E.I. (Enseñanzas Integradas). Vol 6 (3), 1982, págs. 63-69.

