Un potencial delta de Dirac en forma de anillo
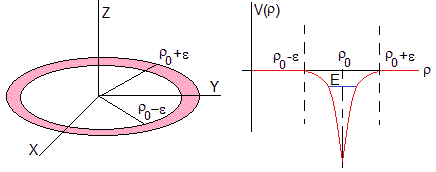
Una partícula de masa m se mueve en un potencial circular
El signo de γ determina si es un pozo (γ>0) o una barrera (γ<0)
Resolvemos la ecuación de Schrödinger en coordenadas cilíndricas independiente de la altura z
Aplicamos el procedimiento de separación de variables
El primer término, solamente depende de ρ, el segundo de φ, la ecuación diferencial se transforma en el sistema de dos ecuaciones diferenciales
La ecuación angular
La solución es
La ecuación radial
Para ρ>ρ0 y para ρ<ρ0, V(ρ)=0
La energía de los niveles E<0
La solución de esta ecuación diferencial (véase el apartado Funciones de Bessel modificadas In y Kn)
La solución de la ecuación diferencial es
-
La función es continua en ρ0
La derivada primera no es continua
Integramos la ecuación diferencial entre los límites ρ0-ε a ρ0+ε donde ε→0
En el límite cuando ε→0
Utilizaremos las siguientes propiedades de las funciones de Bessel
El resultado es una ecuación transcendente
Niveles de energía
Dado el parámetro γ y el radio ρ0 resolvemos la ecuación transcendente
para calcular la energía de los niveles
gamma=5.5;
for n=0:2
f=@(x) gamma*besseli(n,x)*besselk(n,x)-1;
x0=fzero(f,3);
disp(-x0^2)
end
-7.8694
-6.5922
-3.3790
La energía de los niveles se expresa en unidades
Los mismos valores se obtienen para nφ negativa
gamma=5.5;
for n=0:-1:-2
f=@(x) gamma*besseli(n,x)*besselk(n,x)-1;
x0=fzero(f,3);
disp(-x0^2)
end
Funciones de onda
Otra forma equivalente, más adecuda es
El cociente entre los coeficientes se mantiene
Calculamos la constante Cnφ de modo que
Calculamos las integrales partiendo de la ecuación diferencial radial
Integramos por partes el segundo miembro
El resultado es
Fijarse que Im(0)=0 expecepto I0(0)=1
Deshacemos el cambio de variable z=ρk
Seguimos los mismos pasos para evaluar la segunda integral en Knφ
Se ha utilizado los resultados
Comprobamos con MATLAB
>> m=3;
>> z=100;
>> z*(besselk(m+1,z)+besselk(m-1,z))/2
ans = 4.8963e-43
>> z*besselk(m,z)
ans = 4.8699e-43
Deshacemos el cambio de variable, z=ρk
El resultado final es
Resultados
Representamos la componenente radial para nφ=0, 1 y 2, fijados γ=5.5 y ρ0=1
gamma=5.5; %parámetro
r0=1; %radio
hold on
colores=['k','r','g'];
for m=0:2 %números enteros
f=@(x) gamma*besseli(m,x)*besselk(m,x)-1;
k=fzero(f,3);%nivel de energía
d_K=-(besselk(m+1,k*r0)+besselk(m-1,k*r0));
d_I=besseli(m+1,k*r0)+besseli(m-1,k*r0);
den=pi*r0^2*((d_K/besselk(m,k*r0))^2-(d_I/besseli(m,k*r0))^2)/4;
C=sqrt(1/den);
f=@(x) C*besseli(m,k*x)/besseli(m,k*r0);
g=@(x) C*besselk(m,k*x)/besselk(m,k*r0);
fplot(f,[0,r0],colores(m+1))
fplot(g,[r0,3],colores(m+1))
end
grid on
xlabel('\rho/\rho_0')
ylabel('R_n(\rho)')
title('Componente radial')
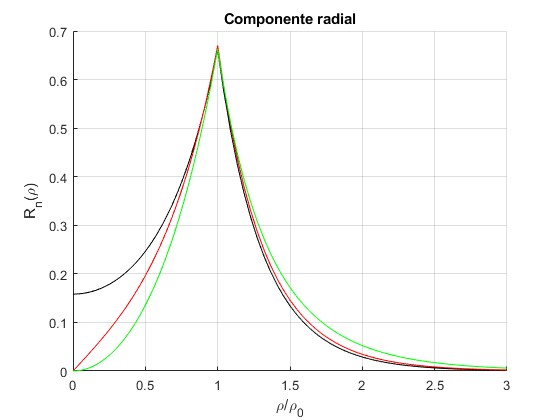
Se representa en color negro l=0, en rojo, l=1 y en verde l=2
Funciones de onda
Se fija el parámetro γ=5.5 y el radio ρ0=1
gamma=5.5; %parámetro
r0=1; %radio
m=0; %número entero
f=@(x) gamma*besseli(m,x)*besselk(m,x)-1;
k=fzero(f,3);
disp(-k^2) %energía
d_K=-(besselk(m+1,k*r0)+besselk(m-1,k*r0));
d_I=besseli(m+1,k*r0)+besseli(m-1,k*r0);
den=pi*r0^2*((d_K/besselk(m,k*r0))^2-(d_I/besseli(m,k*r0))^2)/4;
C=sqrt(1/den);
hold on
rho=linspace(0,r0,50);
phi=linspace(0,2*pi, 100);
[Rho,Phi]=meshgrid(rho,phi);
X=Rho.*cos(Phi);
Y=Rho.*sin(Phi);
Z=C*cos(m*Phi).*besseli(m,k*Rho)/besseli(m,k*r0);
surfl(X,Y,Z)
rho=linspace(r0,3,50);
phi=linspace(0,2*pi, 100);
[Rho,Phi]=meshgrid(rho,phi);
X=Rho.*cos(Phi);
Y=Rho.*sin(Phi);
Z=C*cos(m*Phi).*besselk(m,k*Rho)/besselk(m,k*r0);
surfl(X,Y,Z)
shading interp
colormap(gray);
fplot3(@(t) r0*cos(t), @(t) r0*sin(t), @(t) 0*t, [0,2*pi],'r')
hold off
xlabel('X')
ylabel('Y')
zlabel('Z')
grid on
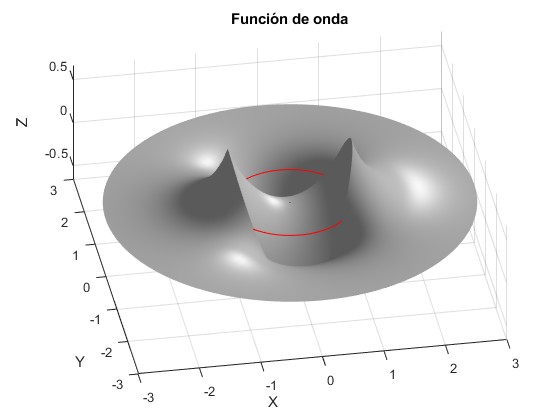
title('Función de onda')
view(-10,60)
Función de onda para nφ=0, (en el código, m=0;), energía E=-7.8694
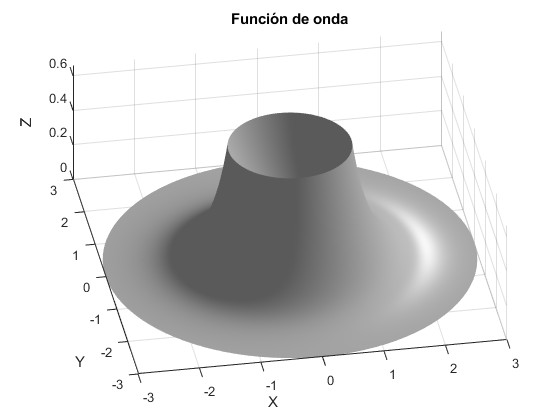
Función de onda para nφ=1, (en el código, m=1;), energía E=-6.5922
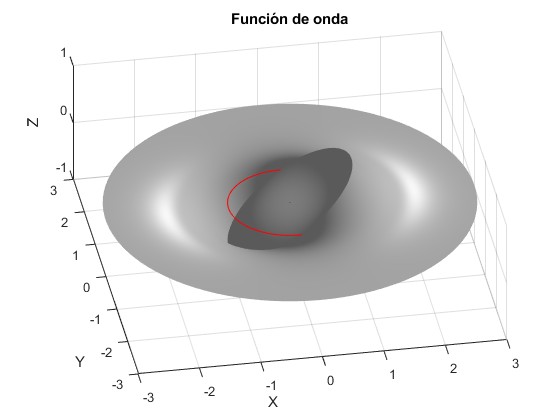
La circuferencia de color rojo, señala la posición del anillo de potencial de profundidad infinita
Función de onda para nφ=2, (en el código, m=2;), energía E=-3.3790
Referencias
Luis F. Castillo-Sánchez, Julio C. Gutiérrez-Vega. Quantum solutions for the delta ring and delta shell. Am. J. Phys. 93 (7), July 2025. pp. 557-565






