Funciones de Bessel
La ecuación diferencial de segundo orden
se conoce como ecuación de Bessel. La solución de esta ecuación diferencial se escribe
donde A y B son constantes que se determinan a partir de las condiciones iniciales. El índice n es un número real, aunque en los libros se proporcionan tablas de las funciones Jn(x) y Yn(x) para valores enteros n=0,1,2,3....
Para n entero se cumple
Funciones de Bessel de primera especie
Representamos J0(x), J1(x), J2(x) y J3(x) llamando a la función
hold on
for n=0:3
f=@(x) besselj(n,x);
fplot(f,[0,20], 'displayName',num2str(n));
end
legend('-DynamicLegend','location','Best')
xlabel('x')
ylabel('J(x)')
title('Funciones J_n(x) de Bessel')
grid on
hold off
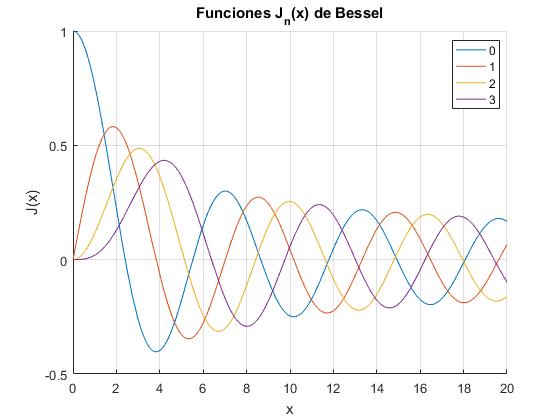
En la siguiente tabla, se proporcionan los primeros ceros de las funciones de Bessel J0(x), J1(x) y J2(x). Utilizamos la función
function bessel_2
x=linspace(0,30,30);
f=@(x) besselj(0,x);
rr=raices(f,x);
disp('J_0(x)')
disp( rr)
f=@(x) besselj(1,x);
rr=raices(f,x);
disp('J_1(x)')
disp (rr)
f=@(x) besselj(2,x);
rr=raices(f,x);
disp('J_2(x)')
disp(rr)
function r = raices(f, x)
y=f(x);
indices=find(y(1:end-1).*y(2:end)<0);
r=zeros(1,length(indices));
for k=1:length(indices)
r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
end
end
end
| J0(x) | J1(x) | J2(x) |
|---|---|---|
| 2.4048 | 3.8317 | 5.1356 |
| 5.5201 | 7.0156 | 8.4172 |
| 8.6537 | 10.1735 | 11.6198 |
| 11.7915 | 13.3237 | 14.7960 |
| 14.9309 | 16.4706 | 17.9598 |
| 18.0711 | 19.6159 | 21.1170 |
| 21.2116 | 22.7601 | 24.2701 |
| 24.3525 | 25.9037 | 27.4206 |
| 27.4935 | 29.0468 | 30.5692 |
| 30.6346 | 32.1897 | 33.7165 |
Aproximaciones
Cuando x se hace grande la función Jn(x), tiende hacia
Representamos la función Jn(x) y su aproximación asintótica
n=3;
f=@(x) sqrt(2./(pi*x)).*cos(x-n*pi/2-pi/4);
k=0:4;
hold on
fplot(@(x) besselj(n,x),[1,20])
fplot(f,[1,20])
r=(2*k+1)*pi/2+n*pi/2+pi/4; %ceros coseno
plot(r,0,'o','markersize',3,'markeredgecolor','r','markerfacecolor','r')
hold off
legend('J_n(x)','cos(x)')
xlabel('x')
ylabel('J_n(x)')
title('Funciones J_n(x) de Bessel')
grid on
hold off
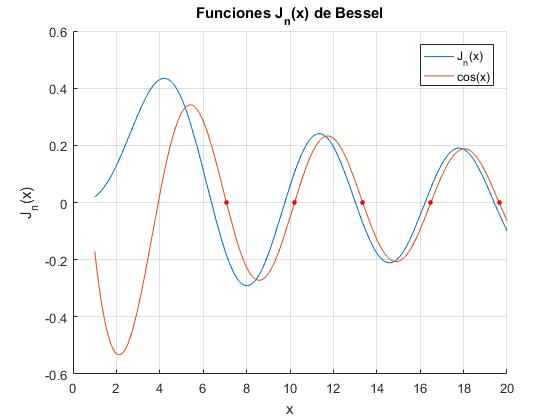
En la figura, se ha representado los ceros de la función cos(x-nπ/2-π/4), que como vemos son próximos a los ceros de la función Jn(x). Este hecho nos permite calcular los ceros de la función de Bessel mediante el comando fzero de MATLAB. Recuérdese que los ceros de la función coseno son (2k+π)/2, k=0,1,2,3...
n=3;
for k=0:5
r=(2*k+1)*pi/2+n*pi/2+pi/4; %ceros coseno
x1=fzero(@(x) besselj(n,x), r);
disp(x1)
end
6.3802
9.7610
13.0152
16.2235
19.4094
22.5827
Relaciones de ortogonalidad
donde km y kl son raíces distintas de Jn(k)=0. Por ejemplo, para n=0
x=linspace(0,40,40); f=@(x) besselj(0,x); k=raices(f,x); f=@(x) x.*(besselj(0,k(1)*x).*besselj(0,k(2)*x)); %raíces distintas integral(f,0,1)
ans = 8.9311e-18
x=linspace(0,40,40); f=@(x) besselj(0,x); k=raices(f,x); f=@(x) x.*(besselj(0,k(2)*x).^2); %segunda raíz de J0 integral(f,0,1)
ans = 0.0579 >> besselj(1,k(2))^2/2 ans = 0.0579
Otras relaciones
para n>-1. Por ejemplo, para n=0
>> syms k x;
>> int('x*besselj(0,k*x)',x,0,1)
ans =besselj(1, k)/k
Derivadas
>> syms x n; >> diff(besselj(n,x)) ans =(n*besselj(n, x))/x - besselj(n + 1, x)
Referencia: I.S. Gradshteyn, I.M. Ryzhik. Table of Integrals, Series, and Products. 2007, Elsevier Inc., apartado 6.561, n° 5, pág. 676, apartado 8.472, n° 1, 2, pág. 926
Desarrollo en serie Fourier-Bessel
En este apartado explicamos el caso más simple, el de una función f(r) tal que f(R)=0 entonces se puede expresar en términos de un desarrollo en serie de Fourier-Bessel
donde kn son los ceros de la función J0(x) o las raíces de la ecuación transcendente J0(k)=0
Para determinar los coeficientes an se utiliza las relaciones de ortogonalidad. Multiplicamos ambos miembros por J0(knr/R) e integramos entre 0 y R
Cuando m≠n la integral se hace cero, resultando
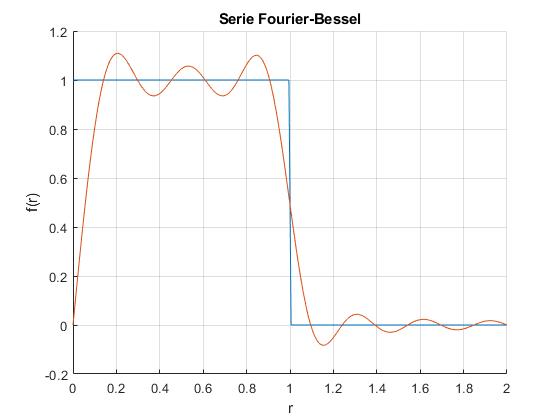
Ejemplo 1
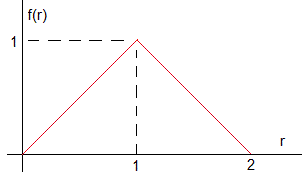
Consideremos la función de la figura, f(r)=1-|r-1| 0≤r≤R=2
Calculamos los coeficientes an
Integramos numéricamente mediante la función
x=linspace(0,40,40);
f=@(x) besselj(0,x);
k=raices(f,x);
R=2;
a=zeros(1,length(k));
for i=1:length(k)
f=@(r) (r.*(1-abs(r-1))).*besselj(0,k(i)*r/R);
a(i)=2*integral(f,0,R)/(R*besselj(1,k(i)))^2;
end
r=linspace(0,R,200);
y=zeros(1,length(r));
for i=1:length(k)
y=y+a(i)*besselj(0,k(i)*r/R);
end
hold on
fplot(@(r) 1-abs(r-1),[0,R]);
plot(r,y);
hold off
grid on
xlabel('r')
ylabel('f(r)')
title('Serie Fourier-Bessel')
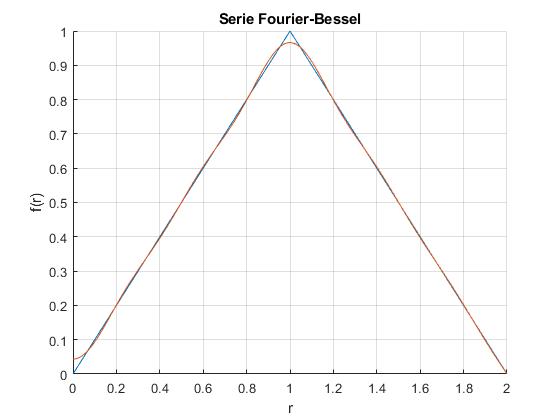
Los valores de los primeros cinco coeficientes son los siguientes:
>> a(1:5) ans = 1.0149 -0.6448 -0.3029 0.0365 0.0865Ejemplo 2
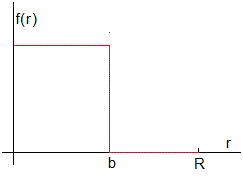
Consideremos la función
Desarrollo en serie en términos de J1(x)
Los coeficientes se calculan del siguiente modo
x=linspace(0,40,40);
f=@(x) besselj(1,x);
k=raices(f,x);
R=2;
b=1;
a=zeros(1,length(k));
for i=1:length(k)
f=@(r) r.*besselj(1,k(i)*r/R);
a(i)=2*integral(f,0,b)/(R*besselj(2,k(i)))^2;
end
r=linspace(0,R,200);
y=zeros(1,length(r));
for i=1:length(k)
y=y+a(i)*besselj(1,k(i)*r/R);
end
yy=r<=b;
hold on
plot(r,yy);
plot(r,y);
hold off
grid on
xlabel('r')
ylabel('f(r)')
title('Serie Fourier-Bessel')
Funciones de Bessel de segunda especie
Representamos Y0(x),Y1(x),Y2(x) llamando a la función
hold on
for n=0:4
fplot(@(x) bessely(n,x),[0.02,15],'displayName',num2str(n));
end
ylim([-2,1])
legend('-DynamicLegend','location','Best')
xlabel('x')
ylabel('Y(x)')
title('Funciones Y_n(x) de Bessel')
grid on
hold off
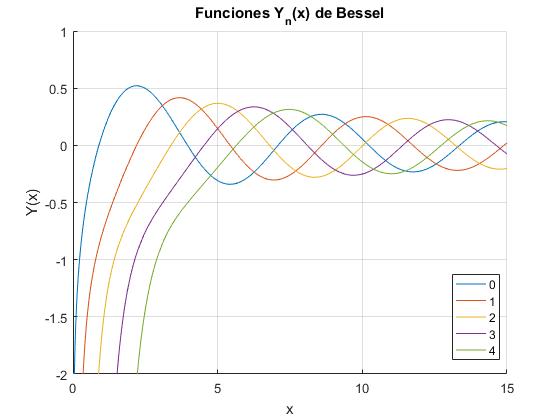
Cuando x se hace grande la función Yn(x), tiende hacia
Derivadas
>> syms x n; >> diff(bessely(n,x)) ans =(n*bessely(n, x))/x - bessely(n + 1, x)
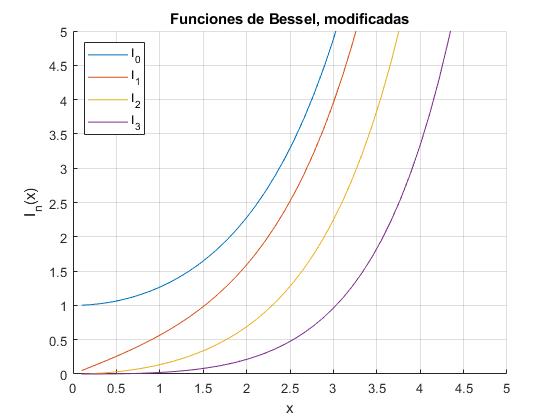
Funciones de Bessel modificadas In y Kn
Son soluciones de la ecuación diferencial
Representamos I0(x), I1(x), I2(x) y I3(x) llamando a la función
hold on
for n=0:3
fplot(@(x) besseli(n,x),[0.1,5])
end
hold off
ylim([0,5])
grid on
legend('I_0','I_1','I_2','I_3', 'location','NorthWest')
xlabel('x')
ylabel('I_n(x)')
title('Funciones de Bessel, modificadas')
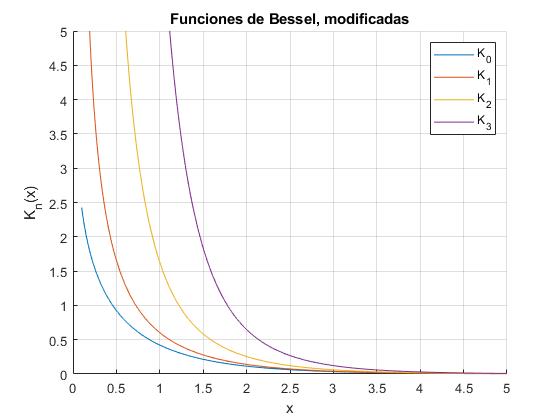
Representamos K0(x), K1(x), K2(x) y K3(x) llamando a la función
hold on
for n=0:3
fplot(@(x) besselk(n,x),[0.1,5])
end
hold off
ylim([0,5])
grid on
legend('K_0','K_1','K_2','K_3')
xlabel('x')
ylabel('K_n(x)')
title('Funciones de Bessel, modificadas')
Derivadas
>> syms x n; >> diff(besseli(n,x)) ans =besseli(n + 1, x) + (n*besseli(n, x))/x >> diff(besselk(n,x)) ans =(n*besselk(n, x))/x - besselk(n + 1, x)
En particular
Alternativamente
Relación entre las dos funciones
Esta relación no aparece en Math Symbolic de MATLAB
>> syms n x; >> besseli(n,x)*besselk(n+1,x)+besseli(n+1,x)*besselk(n,x) ans =besseli(n, x)*besselk(n + 1, x) + besselk(n, x)*besseli(n + 1, x)
Comprobamos con valores numéricos
>> n=3; >> x=[2,4,5,8]; >> besseli(n, x).*besselk(n + 1, x) + besselk(n, x).*besseli(n + 1, x) ans = 0.5000 0.2500 0.2000 0.1250 >> besseli(n, x).*besselk(n - 1, x) + besselk(n, x).*besseli(n - 1, x) ans = 0.5000 0.2500 0.2000 0.1250
Funciones esféricas de Bessel
Las funciones esféricas de Bessel, jn(x) y yn(x) son las dos soluciones independientes de la ecuación diferencial
donde n es un número entero
A y B son coeficientes a determinar a partir de las condciones de contorno
Las funciones esféricas de Bessel, jn(x) y yn(x), están relacionadas con las funciones de Bessel Jn(x) e Yn(x)
Las primeras funciones esféricas de Bessel son
syms x;
for n=-1:3
jn=sqrt(pi/(2*x))*besselj(n+1/2,x);
yn=sqrt(pi/(2*x))*bessely(n+1/2,x);
disp([simplify(jn),simplify(yn)])
end
| jn(x) | yn(x) |
|---|---|
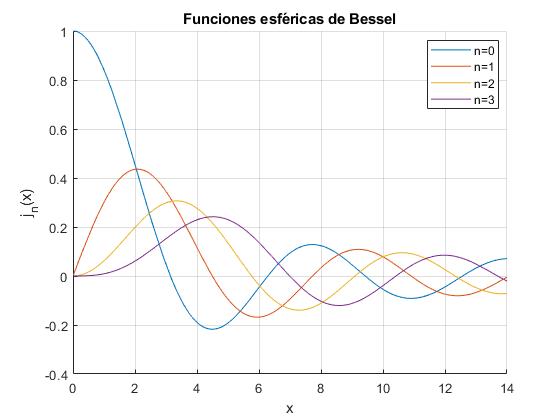
Representamos jn(x) para n=0,1,2,3
hold on
for l=0:3
f=@(x) sqrt(pi./(2*x)).*besselj(l+1/2,x);
fplot(f,[0,14])
end
xlabel('x')
ylabel('j_n(x)')
legend('n=0','n=1','n=2','n=3','Location', 'best')
grid on
title('Funciones esféricas de Bessel')
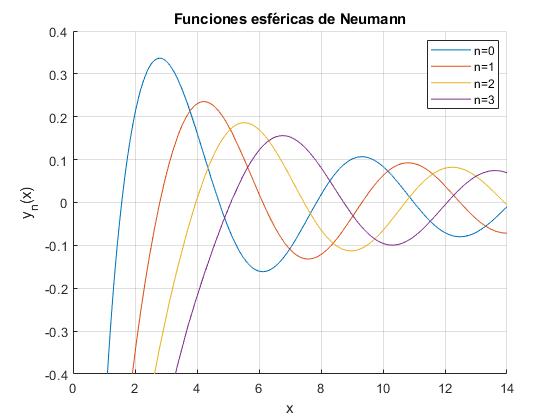
Representamos yn(x) para n=0,1,2,3
hold on
for l=0:3
f=@(x) sqrt(pi./(2*x)).*bessely(l+1/2,x);
fplot(f,[1,14])
end
ylim([-0.4,0.4])
xlabel('x')
ylabel('y_n(x)')
legend('n=0','n=1','n=2','n=3','Location', 'best')
grid on
title('Funciones esféricas de Neumann')
Funciones esféricas de Hankel
Las funciones esféricas de Hankel son
Las primeras funciones son
syms x;
for n=-1:3
hn=sqrt(pi/(2*x))*besselh(n+1/2,1,x);
disp(simplify(hn))
end
Ejemplos en el curso de Física
La ecuación de Laplace, coordenadas cilíndricas (I)
Difracción Fraunhofer producida por una abertura circular
Modos normales de un cable en movimiento de rotación, suspendido verticalmente.
Modos de vibración de una membrana circular
Conducción del calor en un cilindro muy largo (I)
Conducción del calor en un cilindro muy largo (II)
La ecuación de Schrödinger en coordenadas cilíndricas
La ecuación de Schrödinger en coordenadas esféricas (I)
La ecuación de Schrödinger en coordenadas esféricas (II)
Un potencial delta de Dirac en forma de anillo
Movimiento vertical de un cohete con rozamiento (I)
Movimiento vertical de un cohete con rozamiento (II)
Ecuaciones de Navier-Stokes. Estado transitorio (II)
Fluido en un cilindro en rotación, estado transitorio
Condensador concectado a una fuente de corriente alterna

