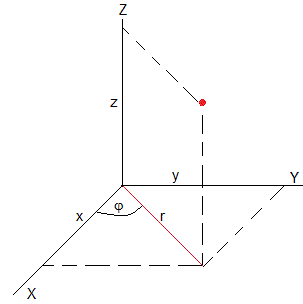
Líneas geodésicas
Supongamos la superficie
La longitud de la línea que une dos puntos A y B y que está contenida en dicha superficie es
Emplemos el cálculo de variaciones para determinar la curva que pasa por los puntos A y B contenida en dicha superficie y cuya longitud L sea mínima. Vamos a considerar dos casos particulares:
P y R son funciones de u y Q=0
P y R son funciones de v y Q=0
La función integrando, , no depende de v. La ecuación de Euler-Lagrange se escribe
La función integrando, , no depende de u. La ecuación de Euler-Lagrange se escribe
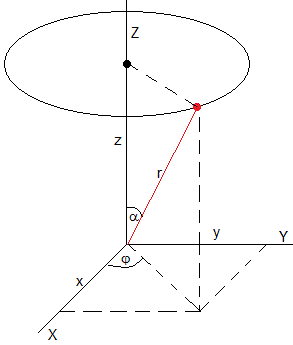
Superficie esférica
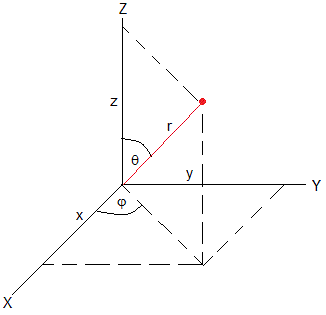
La ecuación de una superficie esférica de radio r es
Para esta superficie, u es φ y v es θ
La longitud de la línea que une dos puntos A y B de la superficie esférica y que está contenida en dicha superficie es
Q=0, P y R son funciones de v=θ. Estamos en el segundo caso con u=φ
Resolvemos la integral
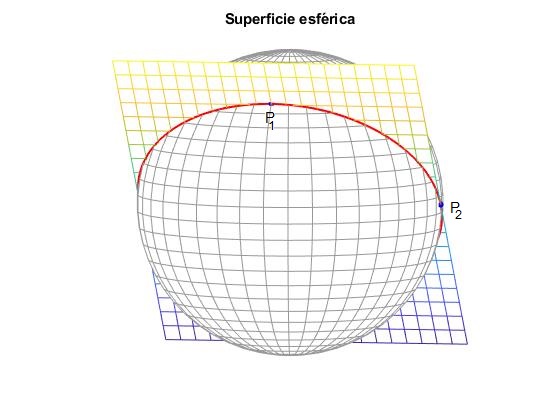
Obtenemos la ecuación del plano que pasa por dos puntos y el origen. Su intersección con la superficie esférica de radio r es una circunferencia máxima
Elegimos dos puntos de la superficie esférica de radio unidad, r=1, especificando sus ángulos (φ, θ).
Determinamos la ecuación del plano que pasa por el origen y por los puntos P1 y P2.
Para trazar la circunferencia máxima, en la ecuación del plano, sustituimos x, y, z en coordenadas polares de radio r=1
Damos valores a φ entre 0 y 2π, obtenemos el ángulo θ, dibujamos el punto de coordenadas (φ,θ), unimos los puntos para trazar la circunferencia máxima que pasa por P1 y P2
Ejemplo
- Punto P1: φ=0, θ=π/4 (45°)
- Punto P2: φ=π/2, θ=π/2 (90°) en el ecuador
phi=linspace(0,pi,30);
theta=linspace(0,2*pi,40);
[phi,theta]=meshgrid(phi,theta);
x=sin(phi).*cos(theta);
y=sin(phi).*sin(theta);
z=cos(phi);
hold on
h1=mesh(x,y,z);
set(h1,'EdgeColor',[0.6,0.6,0.6]);
%punto P1
th=pi/4;
phi=0;
x1=cos(phi)*sin(th);
y1=sin(phi)*sin(th);
z1=cos(th);
plot3(x1,y1,z1,'o','markersize',4,'markeredgecolor','b','markerfacecolor','b')
%punto P2
th=pi/2;
phi=pi/2;
x2=cos(phi)*sin(th);
y2=sin(phi)*sin(th);
z2=cos(th);
plot3(x2,y2,z2,'o','markersize',4,'markeredgecolor','b','markerfacecolor','b')
%plano
A=atan2((y1*z2-y2*z1),(x1*z2-x2*z1));
B=(x1*sin(A)-y1*cos(A))/z1;
[x,y] = meshgrid(-1:0.1:1);
z = (x*sin(A)-y*cos(A))/B;
mesh(x,y,z)
%geodésica
phi=(0:360)*pi/180;
th=atan2(B,sin(A-phi));
plot3(cos(phi).*sin(th),sin(phi).*sin(th),cos(th), 'r','lineWidth',1.5)
axis equal
axis off
view(100,5)
hold off
xlabel('x'); ylabel('y'); zlabel('z')
title('Superficie esférica')
En la figura, vemos los dos puntos en color azul, el plano que pasa por los dos puntos y el origen y su intersección con la superficie esférica de radio unidad, línea gruesa de color rojo
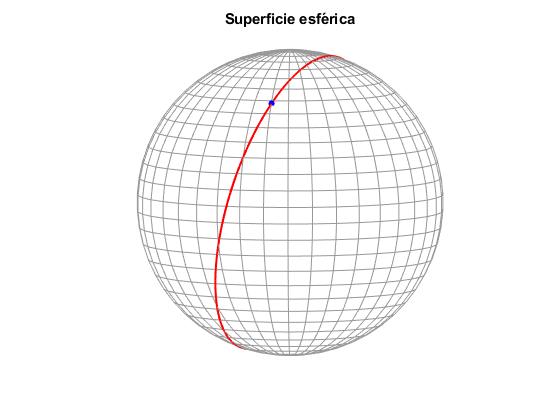
Eliminaremos el plano y dibujaremos los puntos P1 y P2 y la circunferencia que pasa por dichos puntos
Los caso particulares más simples se producen cuando los puntos P1 y P2 están en el mismo meridiano φ=0, la circunferencia máxima es el meridiano. O cuando ambos están en el ecuador, θ=π/2
Otro caso particular, se produce cuando los P1 y P2 están alineados con el origen. P1 y P2 son antípodas. Hay infinitas circunferencias máximas que pasan por los dos puntos
phi=linspace(0,pi,30);
theta=linspace(0,2*pi,40);
[phi,theta]=meshgrid(phi,theta);
x=sin(phi).*cos(theta);
y=sin(phi).*sin(theta);
z=cos(phi);
hold on
h1=mesh(x,y,z);
set(h1,'EdgeColor',[0.6,0.6,0.6]);
%punto P1
th=pi/4;
phi=0;
x1=cos(phi)*sin(th);
y1=sin(phi)*sin(th);
z1=cos(th);
plot3(x1,y1,z1,'o','markersize',4,'markeredgecolor','b','markerfacecolor','b')
%punto P2
th=3*pi/4;
phi=pi;
x2=cos(phi)*sin(th);
y2=sin(phi)*sin(th);
z2=cos(th);
plot3(x2,y2,z2,'o','markersize',4,'markeredgecolor','b','markerfacecolor','b')
%plano
A=atan2((y1*z2-y2*z1),(x1*z2-x2*z1));
B=(x1*sin(A)-y1*cos(A))/z1;
%circunferencia máxima
phi=(0:360)*pi/180;
th=atan2(B,sin(A-phi));
plot3(cos(phi).*sin(th),sin(phi).*sin(th),cos(th), 'r','lineWidth',1.5)
axis equal
axis off
view(100,5)
hold off
xlabel('x'); ylabel('y'); zlabel('z')
title('Superficie esférica')
Longitud del arco que une dos puntos
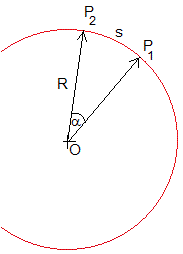
Los vectores que unen el origen con los puntos P1 y P2 de la superficie esférica, son
El producto escalar de estos dos vectores de módulo unidad es
Conocido el ángulo α, la longitud del arco es s=Rα. Siendo R el radio de la superficie terrestre
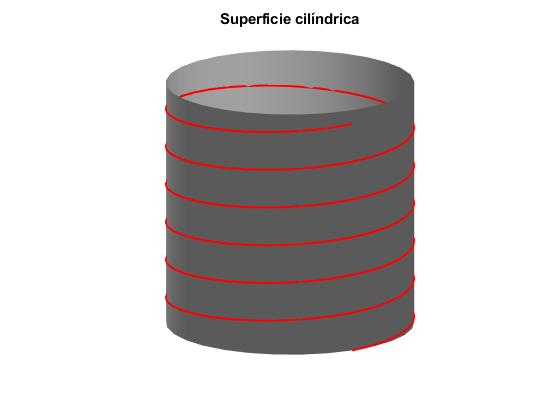
Superficie cilíndrica
La ecuación de una superficie lateral cilíndrica de radio r es
Para esta superficie, u es z y v es φ
La longitud de la línea que une dos puntos A y B de la superficie lateral cilíndrica y que está contenida en dicha superficie es
Q=0, P y R no son funciones de v=φ. Estamos en el primer caso con u=z
Dados dos puntos P1 y P2 de la superficie lateral cilíndrica, calculamos las constantes c2 y c3. Dibujamos una superficie cilíndrica de radio r=1 y la espiral φ=0.05z
r=1*ones(30,1);
phi=linspace(0,2*pi,30);
[r,phi]=meshgrid(r,phi);
x=r.*cos(phi);
y=r.*sin(phi);
z=repmat(linspace(0,2,30),30,1);
hold on
surfl(x,y,z);
shading interp
colormap(gray);
%espiral
th=(0:10:6*360)*pi/180;
plot3(cos(th),sin(th),0.05*th, 'r','lineWidth',1.5)
hold off
axis equal
axis off
xlabel('x'); ylabel('y'); zlabel('z')
title('Superficie cilíndrica')
view(60,15)
Superficie cónica
La ecuación de una superficie cónica de ángulo α es
Para esta superficie, u es r y v es φ
La longitud de la línea que une dos puntos A y B de la superficie cónica y que está contenida en dicha superficie es
Q=0, P y R no son funciones de v=φ. Estamos en el primer caso con u=r
Resolvemos la integral haciendo el cambio de variable, s=rsinα/c1
Hacemos el cambio, s=sect, s=1/cost, ds=sint/cos2t
Deshacemos los cambios y despejamos r
Para una geodésica que pase por los puntos P1 (φ1=0, r1) y P2 (φ2, r2), las constantes c1 y c2, valen
Ejemplo
- Angulo del cono, α=π/3 (60°)
- Punto P1: r1=1, φ1=0
- Punto P2: r2=1, φ2=5π/6 (150°)
alfa=pi/3;
r=linspace(0,1,30);
phi=linspace(0,2*pi,30);
[r,phi]=meshgrid(r,phi);
x=r.*cos(phi)*sin(alfa);
y=r.*sin(phi)*sin(alfa);
z=r*cos(alfa);
hold on
surfl(x,y,z);
shading interp
colormap(gray);
%puntos
r1=1;
r2=1;
th_2=5*pi/6;
c2=atan2((cos(th_2*sin(alfa))-r1/r2),sin(th_2*sin(alfa)));
c1=sin(alfa)*cos(c2)*r1;
%geodésica
th=linspace(0,th_2,100);
r=c1./(sin(alfa)*cos(th*sin(alfa)+c2));
x=r.*cos(th)*sin(alfa);
y=r.*sin(th)*sin(alfa);
z=r*cos(alfa);
plot3(x,y,z,'r','lineWidth',1.5)
hold off
axis off
xlabel('x'); ylabel('y'); zlabel('z')
title('Superficie cónica')
view(47,50)
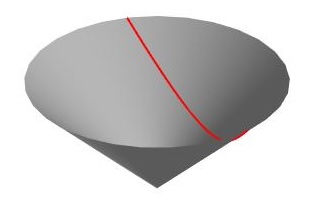
Comprobamos que para obtener la geodésica, el ángulo φ2<π/sinα. Si disminuimos el ángulo α del cono podemos aumentar el ángulo φ2 por encima de 2π, como en este ejemplo
- Angulo del cono, α=π/7 (25.7°)
- Punto P1: r1=1, φ1=0
- Punto P2: r2=1, φ2=6.46 (370°)
Referencias
J Villanueva. Geodesics on surfaces by Variational Calculus. Florida Memorial University, Miami

