Velocidad relativa constante

Un cohete expulsa una fracción m de su combustible a intervalos de tiempos fijos (por ejemplo, cada segundo), con una velocidad u respecto del cohete. Consideraremos que la velocidad u es constante en el sistema de referencia que se mueve con el cohete

Supondremos que el cohete está en el espacio, alejado de cualquier otro cuerpo y por tanto, no actúa ninguna fuerza exterior sobre el mismo. Para calcular la velocidad del cohete a medida que va expulsando el combustible aplicamos el principio de conservación del momento lineal.

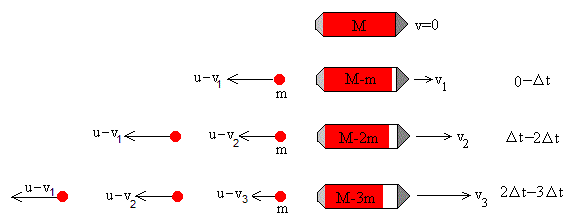
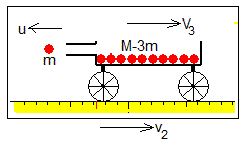
El cohete tiene una masa M que incluye la carga útil, el combustible y la masa del depósito que lo contiene. Supondremos que el cohete expulsa n fracciones de combustible de masa m a intervalos fijos de tiempo, es decir, en los instantes 0, Δt, 2·Δt...(N-1) ·Δt, alcanzando la velocidad en v₁,v₂, ....v_n, tal como se muestra en la figura.

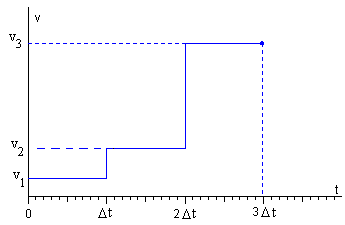
Velocidad del cohete

1. En el intervalo (0-Δt)



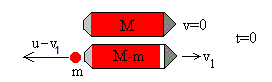
En el instante inicial t=0, el cohete expulsa la primera fracción m de combustible con una velocidad u respecto del cohete. El cohete pierde una masa m y adquiere una velocidad v₁. Si el cohete estaba inicialmente en reposo, su momento lineal es cero. La conservación del momento lineal se escribe.

${\displaystyle \begin{array}{l}\left(M-m\right)v_1+m\left(v_1-u\right)=0\\ v_1=\frac{m}{M}u\end{array}}$

El cohete se moverá con velocidad constante v₁ en el intervalo de tiempo 0-Δt. La fracción m del combustible expulsado se moverá con velocidad constante v₁-u.

La energía necesaria para que el cohete incremente su velocidad a v₁ es

${\displaystyle \Delta E_1=\frac{1}{2}m{\left(v_1-u\right)}^2+\frac{1}{2}(M-m)v_1^2=\frac{1}{2}m{u}^2\left(1-\frac{m}{M}\right)}$

2. En el intervalo (Δt-2Δt)



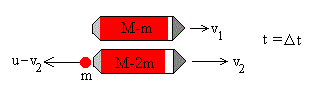
En el instante Δt, el cohete expulsa la segunda fracción m de combustible con velocidad u respecto del cohete o v₂-u respecto de Tierra. El cohete pierde otra masa m y adquiere una velocidad v₂. La conservación del momento lineal se escribe.

${\displaystyle \begin{array}{l}\left(M-2m\right)v_2+m\left(v_2-u\right)=\left(M-m\right)v_1\\ v_2=v_1+\frac{m·u}{M-m}=mu\left(\frac{1}{M}+\frac{1}{M-m}\right)\end{array}}$

El cohete se moverá con velocidad constante v₂ en el intervalo de tiempo Δt -2Δt. La fracción m del combustible expulsado se moverá con velocidad constante v₂-u.

La energía necesaria para que el cohete incremente su velocidad de v₁ a v₂ es

${\displaystyle \Delta E_2=\frac{1}{2}m{\left(v_2-u\right)}^2+\frac{1}{2}(M-2m)v_2^2-\frac{1}{2}(M-m)v_1^2=\frac{1}{2}m{u}^2\left(1-\frac{m}{M-m}\right)}$

3. En el intervalo (2Δt-3Δt)



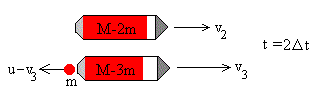
En el instante 2Δt, el cohete expulsa la tercera fracción m de combustible con velocidad u respecto del cohete o v₃-u respecto de Tierra. El cohete pierde otra masa m y adquiere una velocidad v₃. Aplicando el principio de conservación del momento lineal, despejamos v₃.

${\displaystyle \begin{array}{l}\left(M-3m\right)v_3+m\left(v_3-u\right)=\left(M-2m\right)v_2\\ v_3=v_2+\frac{m·u}{M-2m}=mu\left(\frac{1}{M}+\frac{1}{M-m}+\frac{1}{M-2m}\right)\end{array}}$

El cohete se moverá con velocidad constante v₃ en el intervalo de tiempo 2Δt -3Δt. La fracción m del combustible expulsado se moverá con velocidad constante v₃-u.

La energía necesaria para que el cohete incremente su velocidad de v₂ a v₃ es

${\displaystyle \Delta E_3=\frac{1}{2}m{\left(v_3-u\right)}^2+\frac{1}{2}(M-3m)v_3^2-\frac{1}{2}(M-2m)v_2^2=\frac{1}{2}m{u}^2\left(1-\frac{m}{M-2m}\right)}$

4. En el intervalo ((n-1)Δt-nΔt)



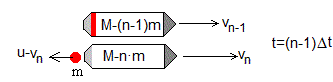
En el instante (n-1)Δt, el cohete expulsa la última fracción m de combustible con velocidad u respecto del cohete o v_n-u respecto de Tierra. El cohete pierde la última masa m y adquiere una velocidad v_n.

${\displaystyle \begin{array}{l}\left(M-nm\right)v_n+m\left(v_n-u\right)=\left(M-(n-1)m\right)v_{n-1}\\ v_n=v_{n-1}+\frac{mu}{M-(n-1)m}\\ v_n=mu\left(\frac{1}{M}+\frac{1}{M-m}+\mathrm{..}+\frac{1}{M-(n-1)·m}\right)=mu{\displaystyle \sum _{i=1}^n\frac{1}{M-(i-1)m}}\end{array}}$

El cohete se moverá con velocidad constante v_n a partir del instante (n-1)Δt. La fracción m del combustible expulsado se moverá con velocidad constante v_n-u.

La energía necesaria para que el cohete incremente su velocidad de v_n-1 a v_n es

${\displaystyle \begin{array}{l}\Delta E_n=\frac{1}{2}m{\left(v_n-u\right)}^2+\frac{1}{2}(M-n·m)v_n^2-\frac{1}{2}(M-(n-1)m)v_{n-1}^2=\\ \frac{1}{2}m{u}^2\left(1-\frac{m}{M-(n-1)m}\right)\end{array}}$

Momento lineal

El momento lineal final del cohete es

P_c=(M-n·m)v_n

El momento lineal del combustible expulsado es la suma (véase la primera figura)

P_g=m(v₁-u)+m(v₂-u)+…m(v_n-u)

La conservación del momento lineal del sistema aislado formado por el cohete y el combustible que expulsa, exige que ambos momentos sean iguales y de sentido contrario. P_c+P_g=0.

Energía

La energía del sistema, es la suma de la energía cinética final del cohete E_c con velocidad v_n, y la energía cinética E_g de las fracciones de masa m de combustible expulsados con velocidades (v₁-u), (v₂-u)… (v_n-u), respectivamente.

${\displaystyle \begin{array}{l}{E}_c=\frac{1}{2}(M-n·m)v_n^2\hfill \\ E_g=\frac{1}{2}{\displaystyle \sum _{i=1}^{n}m{\left(v_i-u\right)}^2}\hfill \end{array}}$

La energía del cohete y la cinética de los gases expulsados es E_c+E_g es también la suma

ΔE₁+ΔE₂+ΔE₃+...+ΔE_n

Desplazamiento

• El desplazamiento en el intervalo de tiempo (0-Δt) es x₁=v₁·Δt
• El desplazamiento en el intervalo de tiempo (Δt-2Δt), vale x₂=v₂·Δt
• El desplazamiento en el intervalo de tiempo (2Δt-3Δt), vale x₃=v₃·Δt

El desplazamiento total en el intervalo de tiempo (0-n·Δt) será

${\displaystyle x={\displaystyle \sum _{i=1}^n{x}_i}=\Delta t·{\displaystyle \sum _{i=1}^n{v}_i}}$

Ejemplo

La masa inicial M del cohete es la suma de la carga útil, más el combustible y la masa del recipiente que será proporcional a la masa del combustible que contiene

masa inicial M =carga útil+(1+r) ·combustible.

donde r es del orden del 5% ó 0.05.

Tomaremos el intervalo de tiempo Δt =1 s. De modo que, la primera fracción de combustible se expulsa en el instante t=0, la segunda en el instante t=1 s., la tercera en el instante t=2 s, y así sucesivamente. El combustible se agota en el instante t=n-1 s.

• Combustible en el cohete, 9000 kg
• Carga útil que transporta, 800 kg.
• Número de fracciones, n=3.

La masa inicial del cohete es (carga útil+combustible+masa del depósito)

M=800+1.05·9000=10250 kg.

La masa de cada fracción de combustible es m=9000/3=3000 kg.

La velocidad con la que se expulsa cada una de las fracciones es u=2000 m/s constante respecto del cohete.

Representamos la velocidad del cohete en los tres intervalos de tiempo (0-1), (1-2), (2,3)

n=3; %fracciones
u=2000; %velocidad de disparo (respecto al móvil)
combustible=9000; %combustible
carga=800;  %carga útil
M=carga+1.05*combustible; %masa total
m=combustible/n; %masa de cada fracción
v=zeros(1,n);
dE=zeros(1,n);
v(1)=m*u/M; %velocidad
line([0,1],[v(1),v(1)])
dE(1)=m*u^2*(1-m/M)/2; %energía
for i=2:n
    v(i)=v(i-1)+m*u/(M-(i-1)*m); %velocidad
    dE(i)=m*u^2*(1-m/(M-(i-1)*m))/2; %energía
    line([i-1,i],[v(i),v(i)])
end
grid on
ylim([0,3000])
xlabel('t(s)')
ylabel('v(m/s)')
title('Velocidad del cohete')

figure %energías 
labels = {'1','2','3'};
pie(dE,labels)
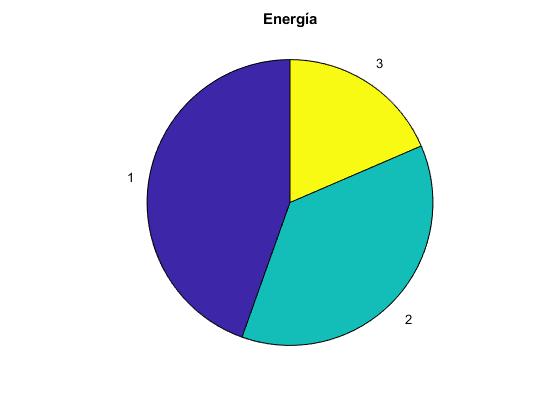
title('Energía')

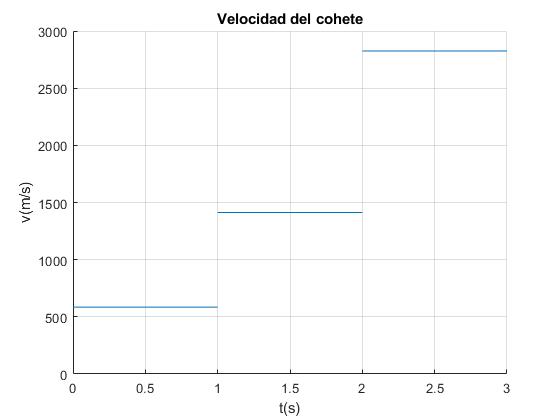
Completamos la siguiente tabla

1. Desplazamiento del cohete en el intervalo de (0- 3) s es el área bajo la curva escalonada, velocidad-tiempo.

>> v(1)+v(2)+v(3)
ans =   4.8230e+03

x=585.4·1+1413.0·1+2824.7·1=4823.0 m.

2. Momento lineal final del cohete

>> (M-3*m)*v(3)
ans =   3.5309e+06

P_c=(10250-3·3000)·2824.7=3.5309·10⁶ kg·m/s

Momento lineal final de los gases expulsados

>> m*(v(1)-u+v(2)-u+v(3)-u)
ans =  -3.5309e+06

P_g=3000·(-1414.6)+3000·(-587.0)+3000·(824.7)=-3.5309·10⁶ kg·m/s.

3. Energías

• Energía del cohete

>> (M-3*m)*v(3)^2/2
ans =   4.9869e+09

E_c=(10250-3·3000)·2824.7²/2=4.9869·10⁹ J

• Energía de los gases expulsados

>> m*((v(1)-u)^2+(v(2)-u)^2+(v(3)-u)^2)/2
ans =   4.5390e+09

E_g=3000·(-1414.6)²/2+3000·(-587.0)²/2+3000·(824.7)²/2=4.5390·10⁹ J

La energía total necesaria para que el cohete alcance la velocidad final de 2824.7 m/s es la suma de ambas contribuciones.

>> (M-3*m)*v(3)^2/2+m*((v(1)-u)^2+(v(2)-u)^2+(v(3)-u)^2)/2
ans =   9.5258e+09

E= E_c+ E_g=9.5258·10⁹ J

La energía E final del cohete y de los gases expulsados es igual a la suma ΔE₁+ΔE₂+ΔE₃.

>> dE(1)+dE(2)+dE(3)
ans =   9.5258e+09

Representamos en un diagrama en forma de tarta, la energía necesaria para incrementar la velocidad del cohete y las fracciones de combustible explulsado

La masa inicial M del cohete incluye, la carga útil, el combustible n·m, dividido en n porciones de masa m y el depósito de forma cilíndrica que lo contiene. Sea f=n·m/M la proporción de combustible respecto a la masa total M inicial del cohete. La velocidad final v_n del cohete en el intervalo (n-1)Δt-nΔt se escribe

${\displaystyle \begin{array}{l}{v}_n=mu{\displaystyle \sum _{i=1}^n\frac{1}{M-(i-1)m}}=u{\displaystyle \sum _{i=1}^n\frac{1}{\frac{nM}{nm}-(i-1)}}=u{\displaystyle \sum _{i=1}^n\frac{1}{\frac{n}{f}-(i-1)}}\\ v_n=uf{\displaystyle \sum _{i=1}^n\frac{1}{n-(i-1)f}}\end{array}}$

Con este código representamos la velocidad del cohete, en los intervalos de tiempo (k-1)Δt-kΔt, k=1,2...n

n=3; %fracciones
f=9000/10250; %combustible/masa inicial
u=2000; %velocidad de disparo (respecto al móvil)
hold on
for k=1:n
    i=1:k;
    v=u*f*sum(1./(n-(i-1)*f)); 
    line([k-1,k],[v,v])
end
hold off
grid on
xlabel('t')
ylabel ('v')
title('Velocidad del cohete')

De la descripción discreta a la continua.

${\displaystyle v_n=mu{\displaystyle \sum _{i=1}^n\frac{1}{M-(i-1)m}}=mu{\displaystyle \sum _{i=1}^n\frac{1}{M-nm+im}}=u{\displaystyle \sum _{i=1}^n\frac{m}{M_f+i·m}}}$

Donde M_f=M-n·m es la masa final del cohete, cuando ha agotado el combustible

En el límite, cuando el cohete pierde masa de forma continua, n es grande y m es una cantidad infinitesimal, por ejemplo, dx. La velocidad final es

${\displaystyle v=u{\displaystyle \underset{0}{\overset{M-M_f}{\int }}\frac{dx}{M_f+x}}=u\ln \left(\frac{M}{M_f}\right)}$

En términos del parámetro f=n·n/M se escribe

${\displaystyle v=u\ln \left(\frac{M}{M-m·n}\right)=u\ln \left(\frac{\frac{M}{m·n}}{\frac{M}{m·n}-1}\right)=u\ln \left(\frac{\frac{1}{f}}{\frac{1}{f}-1}\right)=u\ln \left(\frac{1}{1-f}\right)}$

Para n=3, la velocidad final del cohete cuando ha agotado el combustible, v₃=2824.7 m/s difiere de la aproximación continua, v_f=4208.3 m/s

>> u*log(M/(M-n*m))
ans =   4.2083e+03

Para n=9, la velocidad final v₉=3605.4 m/s, se acerca más a la aproximación continua

Actividades

Se introduce

• El combustible M_c, en el control titulado Combustible en el cohete
• La carga útil que transporta, en el control titulado Carga útil que transporta
• El número n de fracciones de combustible de masa m=M_c/n, que se expulsan a intervalos regulares de tiempo, en el control titulado Número de fracciones
• La velocidad de expulsión de cada una de las fracciones se ha fijado en u=2000 m/s respecto del cohete,

Se pulsa el botón titulado Nuevo

En la parte inferior, vemos el movimiento del cohete (en color azul) y el movimiento de las fracciones de combustible expulsados (en color rojo).

En la parte superior izquierda, tenemos un conjunto de tres barras:

• La primera, señala el tanto por ciento de combustible (en color blanco) gastado y en color rojo el remanente.
• La segunda representa, el momento lineal del cohete (azul) y el momento lineal de los gases expulsados (en rojo), ambos momentos son iguales y de sentido contrario, de modo que el momento lineal total es cero.
• La tercera barra, representa la energía: la longitud total de la barra es la energía total disponible, la parte azul corresponde a la energía cinética del cohete y la parte roja, la energía cinética de las fracciones de combustible expulsadas.

Finalmente, tenemos la representación de la velocidad del cohete en función del tiempo. En color rojo la curva continua describe el perfil de la velocidad del cohete calculada siguiendo el modelo continuo, que describiremos en las siguientes páginas. En color azul, tenemos una curva escalonada que representa el perfil de la velocidad del cohete calculada siguiendo el modelo discreto descrito en este apartado.

A medida que se incrementa el número n de fracciones, las predicciones del modelo discreto se acercan a las del modelo continuo.

Energía constante

1. En el intervalo (0-Δt)



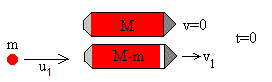
En el instante inicial t=0, el cohete expulsa la primera fracción m de combustible con una velocidad u₁ respecto a Tierra. El cohete pierde una masa m de combustible y adquiere una velocidad v₁. Si el cohete estaba inicialmente en reposo, su momento lineal es cero. La conservación del momento lineal se escribe.

(M-m)v₁+mu₁=0

${\displaystyle u_1=-\frac{M-m}{m}{v}_1}$

El cohete se moverá con velocidad constante v₁ en el intervalo de tiempo 0-Δt. La fracción m del combustible expulsado se moverá con velocidad constante u₁ en sentido contrario.

La energía necesaria para proporcionar estas velocidades será

${\displaystyle \Delta E_1=\frac{1}{2}m{u}_1^2+\frac{1}{2}(M-m)v_1^2=\frac{1}{2}\frac{M(M-m)}{m}{v}_1^2}$

Supongamos que la energía ΔE₁=αm la proporciona una fracción α del combustible expulsado. Despejamos la velocidad del cohete v₁

${\displaystyle v_1=\sqrt{\frac{2\alpha }{M(M-m)}}m}$

2. En el intervalo (Δt-2Δt)



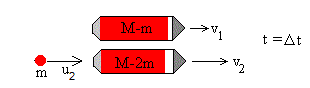
En el instante Δt, el cohete expulsa la segunda fracción m de combustible con velocidad u₂ respecto de Tierra. El cohete pierde otra masa m de combustible y adquiere una velocidad v₂. La conservación del momento lineal se escribe.

(M-2m)v₂+mu₂=(M-m)v₁

${\displaystyle u_2=\frac{(M-m)v_1-(M-2m)v_2}{m}}$

El cohete se moverá con velocidad constante v₂ en el intervalo de tiempo Δt-2Δt. La fracción m del combustible expulsado se moverá con velocidad constante u₂.

La energía necesaria para proporcionar estas velocidades será

${\displaystyle \Delta E_2=\frac{1}{2}m{u}_2^2+\frac{1}{2}(M-2m)v_2^2-\frac{1}{2}(M-m)v_1^2=\frac{1}{2}\frac{(M-2m)(M-m)}{m}{\left(v_2-v_1\right)}^2}$

Supongamos que la energía ΔE₂=αm la proporciona una fracción α del combustible expulsado. Despejamos la velocidad del cohete v₂

${\displaystyle v_2=v_1+\sqrt{\frac{2\alpha }{(M-m)(M-2m)}}m}$

3. En el intervalo (2Δt-3Δt)



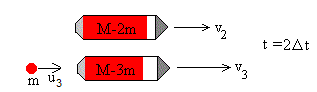
En el instante 2Δt, el cohete expulsa la tercera fracción m de combustible con velocidad u₃ respecto de Tierra. El cohete pierde otra masa m de combustible y adquiere una velocidad v₃. El principio de conservación del momento lineal se escribe,

(M-3m)v₃+mu₃=(M-2m)v₂

${\displaystyle u_3=\frac{(M-2m)v_2-(M-3m)v_3}{m}}$

El cohete se moverá con velocidad constante v₃ en el intervalo de tiempo 2Δt-3Δt. La fracción m del combustible expulsado se moverá con velocidad constante u₃.

La energía necesaria para proporcionar estas velocidades será

${\displaystyle \Delta E_3=\frac{1}{2}m{u}_3^2+\frac{1}{2}(M-3m)v_3^2-\frac{1}{2}(M-2m)v_2^2=\frac{1}{2}\frac{(M-3m)(M-2m)}{m}{\left(v_3-v_2\right)}^2}$

Supongamos que la energía ΔE₃=αm la proporciona una fracción α del combustible expulsado. Despejamos la velocidad del cohete v₃

${\displaystyle v_3=v_2+\sqrt{\frac{2\alpha }{(M-2m)(M-3m)}}m}$

4. En el intervalo ((n-1)Δt-nΔt)



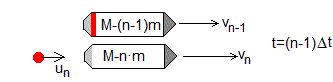
En el instante (n-1)Δt, el cohete expulsa la última fracción m de combustible con velocidad u_n respecto de Tierra. El cohete pierde otra masa m de combustible y adquiere una velocidad v_n.

${\displaystyle u_n=\frac{\left(M-(n-1)m\right)v_{n-1}-(M-n·m)v_n}{m}}$

El cohete se moverá con velocidad constante v_n desde el instante (n-1)Δt. La fracción m del combustible expulsado se moverá con velocidad constante u_n.

La energía necesaria para proporcionar estas velocidades será

${\displaystyle \begin{array}{l}\Delta E_n=\frac{1}{2}m{u}_n^2+\frac{1}{2}(M-n·m)v_n^2-\frac{1}{2}\left(M-(n-1)m\right)v_{n-1}^2\\ =\frac{1}{2}\frac{(M-n·m)\left(M-(n-1)m\right)}{m}{\left(v_n-v_{n-1}\right)}^2\end{array}}$

Supongamos que la energía ΔE_n=αm la proporciona una fracción α del combustible expulsado. Despejamos la velocidad del cohete v_n

${\displaystyle \begin{array}{l}{v}_n=v_{n-1}+\sqrt{\frac{2\alpha }{\left(M-(n-1)m\right)(M-n·m)}}m\\ v_n=\sqrt{2\alpha }{\displaystyle \sum _{i=1}^n\sqrt{\frac{m^2}{\left(M-(i-1)m\right)(M-i·m)}}}\end{array}}$

La masa inicial M del cohete incluye, la carga útil, el combustible n·m, dividido en n porciones de masa m y el depósito de forma cilíndrica que lo contiene. Sea f=nm/M la proporción de combustible respecto a la masa total M inicial del cohete. La velocidad final v_n del cohete en el intervalo (n-1)Δt-nΔt se escribe

${\displaystyle \begin{array}{l}{v}_n=\sqrt{2\alpha }{\displaystyle \sum _{i=1}^n\sqrt{\frac{1}{\left(\frac{nM}{nm}-(i-1)\right)\left(\frac{nM}{nm}-i\right)}}}=\sqrt{2\alpha }{\displaystyle \sum _{i=1}^n\sqrt{\frac{1}{\left(\frac{n}{f}-(i-1)\right)\left(\frac{n}{f}-i\right)}}}\\ v_n=\sqrt{2\alpha }f{\displaystyle \sum _{i=1}^n\frac{1}{\sqrt{\left(n-(i-1)f\right)(n-i·f)}}}\end{array}}$

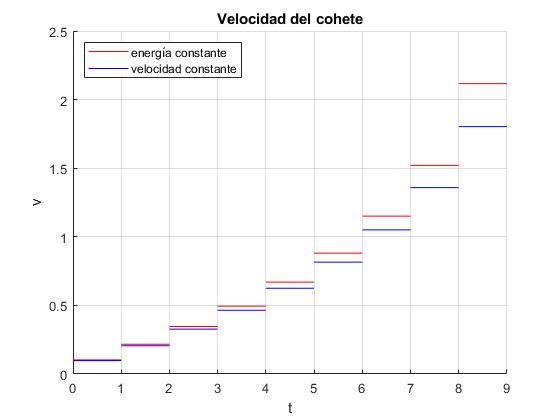
Representamos la velocidad $\frac{v_k}{\sqrt{2\alpha }}$, (aproximación de energía constante) y la comparamos con la velocidad v_k/u obtenida en el primer apartado (aproximación de velocidad u relativa constante) en los intervalos de tiempo (k-1)Δt-kΔt, k=1,2...n. Observamos que la primera es mayor que la segunda

n=9; %fracciones
f=9000/10250; %combustible/masa inicial
hold on
for k=1:n
     i=1:k;
    v=f*sum(1./sqrt((n-(i-1)*f).*(n-i*f))); %energía constante
    line([k-1,k],[v,v],'color','r')
    v=f*sum(1./(n-(i-1)*f)); %velocidad constante
    line([k-1,k],[v,v],'color','b')
end
hold off
grid on
xlabel('t')
legend('energía constante','velocidad constante','location','northwest')
ylabel ('v')
title('Velocidad del cohete')

De la descripción discreta a la continua.

Cuando el número de fracciones n es grande

${\displaystyle \begin{array}{l}{v}_n=\sqrt{2\alpha }f{\displaystyle \sum _{i=1}^n\frac{1}{\sqrt{\left(n-i·f-f\right)(n-i·f)}}}\approx \sqrt{2\alpha }f{\displaystyle \sum _{i=1}^n\frac{1}{\sqrt{\left(n-i·f\right)(n-i·f)}}}\\ =\sqrt{2\alpha }{\displaystyle \sum _{i=1}^n\frac{f}{n-i·f}}=\sqrt{2\alpha }{\displaystyle \sum _{i=1}^n\frac{\frac{f}{n}}{1-i·\frac{f}{n}}}\end{array}}$

En el límite cuando n→∞

${\displaystyle v_n\approx \sqrt{2\alpha }{\displaystyle \underset{0}{\overset{f}{\int }}\frac{dx}{1-x}}=-\sqrt{2\alpha }\ln \left(1-f\right)=\sqrt{2\alpha }\ln \left(\frac{1}{1-\frac{n·m}{M}}\right)=u\ln \left(\frac{M}{M_f}\right)}$

Donde M_f=M-n·m es la masa final del cohete, cuando ha agotado el combustible. Obtenemos la misma expresión que en el apartado anterior, si establecemos la relación entre el parámetro α y la velocidad relativa constante u

${\displaystyle \sqrt{2\alpha }=u,\alpha =\frac{1}{2}{u}^2}$

Impulso constante

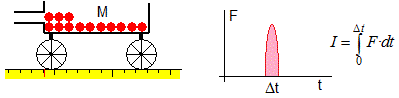
Una bola de masa m inicialmente en reposo es golpeada por la raqueta de un tenista, que le porporciona un impulso (una fuerza F intensa durante un corto intervalo de tiempo Δt) de módulo I=mu, la pelota modifica su momento lineal en mu, siendo u su velocidad inmediatamente después de ser golpeada

Supongamos un carro inicialmente en reposo, de masa M que contiene n bolas de masa m cada una. El carro tiene un dispositivo que proporciona un impulso m·u a la bola que dispara y a su vez este impulso modifica la velocidad del carro cuya masa ha disminuido en m.

Velocidad del carro

1. En el intervalo (0-Δt)



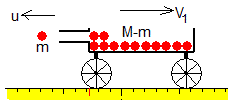
En el instante inicial t=0, el carro dispara la primera bola de masa m con una velocidad u. El carro pierde una masa m y adquiere una velocidad V₁. Si el carro estaba inicialmente en reposo, su momento lineal es cero. El impulso I=mu modifica su momento lineal.

${\displaystyle \begin{array}{l}(M-m)V_1=mu\\ V_1=\frac{mu}{M-m}\end{array}}$

Como el carro estaba inicialmente en reposo, la velocidad de la bola respecto a Tierra es u₁=-u y la del carro v₁=V₁

La variación de energía antes y despues del disparo de la bola es

${\displaystyle \Delta E_1=\frac{1}{2}m{u}^2+\frac{1}{2}(M-m)V_1^2=\frac{1}{2}m{u}^2\left(1+\frac{m}{M-m}\right)}$

2. En el intervalo (Δt-2Δt)



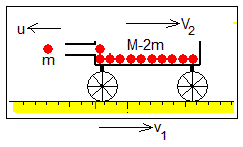
Nos situamos en el sistema de referencia que se mueve con el carro a velocidad v₁

En el instante Δt, el carro dispara la segunda bola con velocidad u. El carro pierde otra masa m y adquiere una velocidad V₂. El impulso I=mu modifica su momento lineal

(M-2m)V₂=mu

Las velocidades del carro y de la bola respecto de Tierra son

${\displaystyle \begin{array}{l}{v}_2=v_1+V_2=v_1+\frac{mu}{M-2m}=mu\left(\frac{1}{M-m}+\frac{1}{M-2m}\right)\\ u_2=-u+v_1=-u+\frac{mu}{M-m}\end{array}}$

La variación de energía antes y despues del disparo de la bola es

${\displaystyle \Delta E_2=\frac{1}{2}m{u}^2+\frac{1}{2}(M-2m)V_2^2=\frac{1}{2}m{u}^2\left(1+\frac{m}{M-2m}\right)}$

3. En el intervalo (2Δt-3Δt)



Nos situamos en el sistema de referencia que se mueve con el carro a velocidad v₂

En el instante 2Δt, el carro dispara la tercera bola con velocidad u. El carro pierde otra masa m y adquiere una velocidad V₃.

(M-3m)V₃=mu

Las velocidades del carro y de la bola respecto de Tierra son

${\displaystyle \begin{array}{l}{v}_3=v_2+V_3=v_2+\frac{mu}{M-3m}=mu\left(\frac{1}{M-m}+\frac{1}{M-2m}+\frac{1}{M-3m}\right)\\ u_3=-u+v_2=-u+mu\left(\frac{1}{M-m}+\frac{1}{M-2m}\right)\end{array}}$

La variación de energía antes y despues del disparo de la bola es

${\displaystyle \Delta E_3=\frac{1}{2}m{u}^2+\frac{1}{2}(M-3m)V_3^2=\frac{1}{2}m{u}^2\left(1+\frac{m}{M-3m}\right)}$

4. En el intervalo ((n-1)Δt-nΔt)



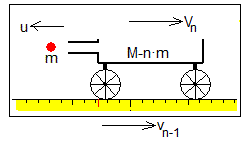
Nos situamos en el sistema de referencia que se mueve con el carro con velocidad v_n-1

En el instante (n-1)Δt, el carro dispara la última bola con velocidad u. El cohete pierde la última bola y adquiere una velocidad V_n.

(M-n·m)V_n=mu

Las velocidades del carro y de la bola respecto de Tierra son

${\displaystyle \begin{array}{l}{v}_n=v_{n-1}+V_n=v_{n-1}+\frac{mu}{M-nm}=mu\left(\frac{1}{M-m}+\frac{1}{M-2m}+\mathrm{...}+\frac{1}{M-n·m}\right)\\ u_n=-u+v_{n-1}=-u+mu\left(\frac{1}{M-m}+\frac{1}{M-2m}+\mathrm{...}+\frac{1}{M-(n-1)·m}\right)\end{array}}$

La variación de energía antes y despues del disparo de la bola es

${\displaystyle \Delta E_n=\frac{1}{2}m{u}^2+\frac{1}{2}(M-n·m)V_n^2=\frac{1}{2}m{u}^2\left(1+\frac{m}{M-n·m}\right)}$

Sea f=n·m/M la proporción de las masas de las bolas a la masa total inicial M del carro. La velocidad final v_n del carro en el intervalo (n-1)Δt-nΔt se escribe

${\displaystyle v_n=u{\displaystyle \sum _{i=1}^n\frac{m}{M-i·m}}=u{\displaystyle \sum _{i=1}^n\frac{1}{\frac{nM}{n·m}-i}=}u{\displaystyle \sum _{i=1}^n\frac{1}{\frac{n}{f}-i}=}u{\displaystyle \sum _{i=1}^n\frac{f}{n-f·i}}}$

Momento lineal

En momento lineal final del carro es

P_c=(M-n·m)v_n

El momento lineal de las bolas disparadas es

${\displaystyle P_g=m\left(-u+(-u+v_1)+(-u+v_2)+\mathrm{....}+(-u+v_{n-1})\right)}$

La conservación del momento lineal del sistema aislado formado por el carro y las n bolas que dispara, exige que ambos momentos sean iguales y de sentido contrario. P_c+P_g=0.

Energía

La energía del sistema, es la suma de la energía cinética del carro E_c con velocidad v_n, y la energía cinética E_g de las bolas disparadas con velocidad (-u), (-u+v₁), (-u+v₂),...(-u+v_n-1), respectivamente.

${\displaystyle \begin{array}{l}{E}_c=\frac{1}{2}(M-n·m)v_n^2\\ E_g=\frac{1}{2}m{u}^2+\frac{1}{2}m{\displaystyle \sum _{i=1}^{n-1}{\left(-u+v_i\right)}^2}\end{array}}$

La energía del carro y las bolas dispardas es E_c+E_g es también la suma

ΔE₁+ΔE₂+ΔE₃+...+ΔE_n

Comprobaciones

Utilizaremos los datos del ejemplo del primer apartado

Tomaremos el intervalo de tiempo Δt =1 s. De modo que, la primera bola se dispara en el instante t=0, la segunda en el instante t=1 s., la tercera en el instante t=2 s, y así sucesivamente. Las bolas desaparecen el instante t=n-1 s.

• Masa de las bolas, 9000 kg
• Masa del carro vacío, 1250 kg.
• Número de bolas, n=3.

La masa inicial del carro es M=1250+9000=10250 kg

La masa de cada bola es m=9000/3=3000 kg.

El impulso constante que se proporciona a cada una de las bolas y al carro es m·u=3000·2000 kg·m/s .

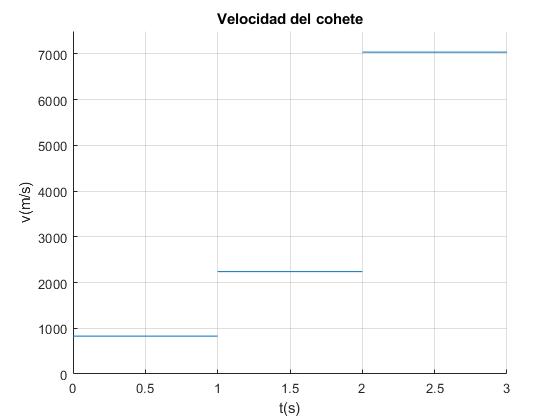
Representamos la velocidad del carro en los tres intervalos de tiempo (0-1), (1-2), (2,3)

n=3; %fracciones
u=2000; %velocidad de disparo (respecto al móvil)
m=9000/n; %masa de cada bola
M=1250+9000; %masa inicial
v=zeros(1,n);
dE=zeros(1,n);
v(1)=m*u/(M-m); %velocidad
line([0,1],[v(1),v(1)])
dE(1)=m*u^2*(1+m/(M-m))/2; %energía
for i=2:n
    v(i)=v(i-1)+m*u/(M-i*m); %velocidad
    dE(i)=m*u^2*(1+m/(M-i*m))/2; %energía
    line([i-1,i],[v(i),v(i)])
end
grid on
%ylim([0,7500])
xlabel('t(s)')
ylabel('v(m/s)')
title('Velocidad del cohete')

figure %energías 
labels = {'1','2','3'};
pie(dE,labels)
title('Energía')

1. Momento lineal final del carro

>> (M-3*m)*v(3)
ans =   8.7992e+06

Momento lineal final de bolas disparadas

>> m*(-u)+m*(-u+v(1))+m*(-u+v(2))
ans =  -8.7992e+06

2. Energías

Energía final del carro y de las bolas disparadas

>> (M-3*m)*v(3)^2/2+m*((-u)^2+(-u+v(1))^2+(-u+v(2))^2)/2
ans =   3.9118e+10

La energía E final del carro y de las bolas disparadas es igual a la suma ΔE₁+ΔE₂+ΔE₃.

>> dE(1)+dE(2)+dE(3)
ans =   3.9118e+10

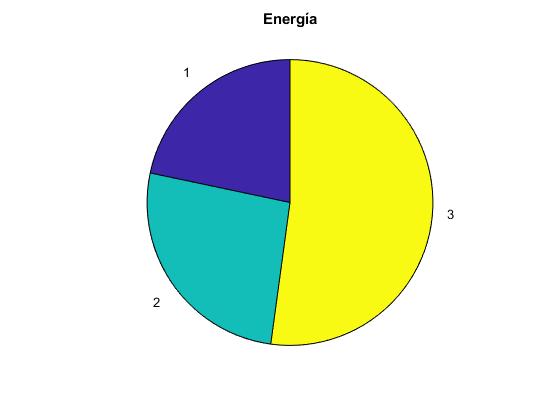
Representamos en un diagrama en forma de tarta, la energía necesaria para incrementar la velocidad del carro y las bolas disparadas

Actividades

Se introduce

• La masa del vehículo vacío, en el control titulado Masa vacío
• La masa m del proyectil, en el control titulado Masa bala
• El número n de proyectiles, en el control titulado Número de balas
• Velocidad de disparo del proyectil respecto del vehículo se ha fijado en u=10 m/s

Se pulsa el botón titulado Nuevo.

La masa inicial del vehículo M es la suma de la masa del vehículo vacío y de los proyectiles

Los proyectiles se disparan consecutivamente separados un segundo

En la parte superior, se representa la velocidad del vehículo en función del número de disparo.

Cuando se han terminado de disparar todos los proyectiles el vehículo se mueve con velocidad constante.

Ejemplo

• Masa del vehículo vacío M=20 kg
• Masa del proyectil m=1 kg
• Impulso constante m·u=10 kg·m/s
• Número de proyectiles n=5.

El vehículo de masa inicial M+n·m=25 kg parte del reposo

Calculamos las velocidades del vehículo en cada intervalo de tiempo

n=5; %fracciones
m=1; %masa de cada bola
u=10; %impulso
M=20+n*m; %masa inicial
v=zeros(1,n);
v(1)=m*u/(M-m); %velocidad
for i=2:n
    v(i)=v(i-1)+m*u/(M-i*m); %velocidad
end
disp(v)

    0.4167    0.8514    1.3060    1.7822    2.2822

Comparación de los tres modelos

Representamos la velocidad final del cohete v_n en función del número de fracciones n de acuerdo con el modelo:

• Velocidad relativa u constante (color azul)
• Energía constante (color rojo)
• Impulso constante (color negro)

La recta horizontal de color negro es el límite continuo, cuando el número de fracciones tiende a infinito

f=9000/10250; %combustible/masa inicial
hold on
for n=1:50
     i=1:n;
     v=f*sum(1./sqrt((n-(i-1)*f).*(n-i*f))); %energía constante
     plot(n,v,'ro','markersize',3,'markeredgecolor','r','markerfacecolor','r')
     v=f*sum(1./(n-(i-1)*f)); %velocidad constante
     plot(n,v,'bo','markersize',3,'markeredgecolor','b','markerfacecolor','b')
     v=f*sum(1./(n-i*f)); %impulso constante
     plot(n,v,'ko','markersize',3,'markeredgecolor','k','markerfacecolor','k')
end
v_lim=log(1/(1-f)); %continuo
line([0,50],[v_lim,v_lim],'color','k')
hold off
grid on
xlabel('n')
ylabel ('v')
title('Velocidad final del cohete')

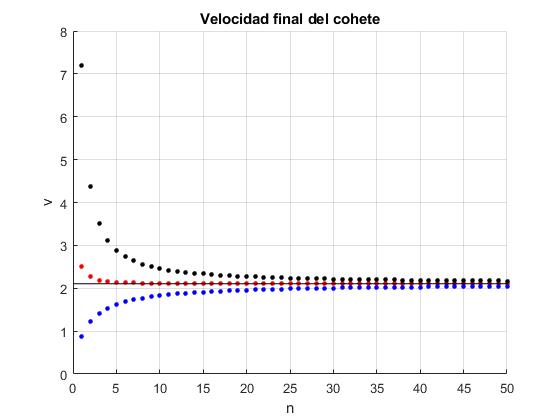
Vemos en la gráfica, que el primer modelo de velocidad relativa constante predice la mínima velocidad final para n=1, una sola fracción, mientras que los otros dos modelos predicen que la máxima velocidad final del cohete.

Cuando el número n de fracciones se hace grande, los tres modelos tienden a la velocidad predicha por el modelo continuo, pero el modelo discreto de energía constante es el que mejor se ajusta

Referencias

Bose S. K. The rocket problem revisited. Am. J. Phys. 51 (5) 1983, pp. 463-464

Philip R Blanco. A discrete, energetic approach to rocket propulsion. Phys. Educ. 54 (2019) 065001

Brun J. L. Motion of a trolley powered by ejecting balls. Eur. J. Phys. 27 (2006) pp. 1357-1362