Movimiento sobre la superficie cónica

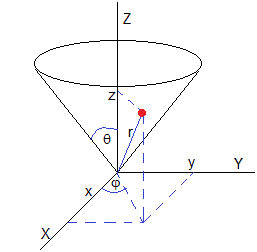
Consideremos una partícula de masa m que se puede mover sobre una superficie cónica de ángulo 2θ bajo la acción de su propio peso. En un instante dado t, la partícula dista r del vértice del cono y hace un ángulo φ con el eje X tal como se muestra en la figura. Describimos el movimiento de la partícula en coordenadas esféricas (r, φ, θ) con el ángulo θ constante.

La posición de la partícula es

${\displaystyle \{\begin{array}{l}x=r\sin \theta \cos \phi \\ y=r\sin \theta \sin \phi \\ z=r\cos \theta \end{array}}$

Derivando con respecto del tiempo obtenemos las componentes de la velocidad

${\displaystyle \{\begin{array}{l}\frac{dx}{dt}=\frac{dr}{dt}\sin \theta \cos \phi -r\sin \theta \sin \phi \frac{d\phi }{dt}\\ \frac{dy}{dt}=\frac{dr}{dt}\sin \theta \sin \phi +r\sin \theta \cos \phi \frac{d\phi }{dt}\\ \frac{dz}{dt}=\frac{dr}{dt}\cos \theta \end{array}}$

La energía cinética es

${\displaystyle T=\frac{1}{2}m\left({\left(\frac{dx}{dt}\right)}^2+{\left(\frac{dy}{dt}\right)}^2+{\left(\frac{dz}{dt}\right)}^2\right)=\frac{1}{2}m\left({\left(\frac{dr}{dt}\right)}^2+r^2{\sin }^2\theta {\left(\frac{d\phi }{dt}\right)}^2\right)}$

La energía potencial es V=mgz=mgrcosθ

La lagrangiana L=T-V es

${\displaystyle \begin{array}{l}L=\frac{1}{2}m\left({\left(\frac{dr}{dt}\right)}^2+r^2{\sin }^2\theta {\left(\frac{d\phi }{dt}\right)}^2\right)-mgr\cos \theta \\ L=\frac{1}{2}m\left({\dot{r}}^2+r^2{\sin }^2\theta ·{\dot{\phi }}^2\right)-mgr\cos \theta \end{array}}$

Ecuaciones del movimiento

La primera ecuación del movimiento es

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{r}}\right)-\frac{\partial L}{\partial r}=0\\ \frac{d^{2}r}{d{t}^2}-r{\sin }^2\theta {\left(\frac{d\phi }{dt}\right)}^2+g\cos \theta =0\end{array}}$

La segunda ecuación del movimiento es

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\phi }}\right)-\frac{\partial L}{\partial \phi }=0\\ r^2{\sin }^2\theta \frac{d^2\phi }{d{t}^2}=0\end{array}}$

Principios de conservación

Como la lagrangiana L es independiente de φ, obtenemos una cantidad h que se conserva

${\displaystyle r^2{\sin }^2\theta \frac{d\phi }{dt}=h}$

Comprobamos que h está relacionado con la componente Z del momento angular $\overrightarrow{L}=\overrightarrow{r}\times m\overrightarrow{v}$

${\displaystyle L_z=m\left(x\frac{dy}{dt}-y\frac{dx}{dt}\right)=m{r}^2{\sin }^2\theta \frac{d\phi }{dt}}$

La ecuación del movimiento en la dirección radial se convierte en

${\displaystyle \frac{d^{2}r}{d{t}^2}-\frac{h^2}{r^3{\sin }^2\theta }+g\cos \theta =0}$

que a su vez es la derivada con respecto del tiempo de una cantidad que se conserva

${\displaystyle \frac{d}{dt}\left(\frac{1}{2}{\left(\frac{dr}{dt}\right)}^2+\frac{h^2}{2r^2{\sin }^2\theta }+gr\cos \theta \right)=0}$

La conservación de la energía ε se expresa

${\displaystyle \frac{1}{2}{\left(\frac{dr}{dt}\right)}^2+\frac{h^2}{2r^2{\sin }^2\theta }+gr\cos \theta =\epsilon }$

Energía potencial efectiva

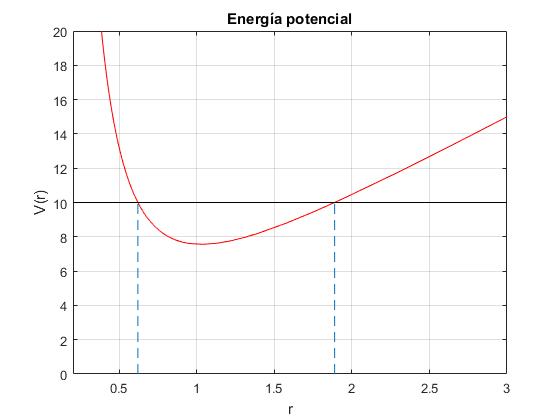
V(r) es la energía potencial efectiva para el movimiento en la dirección radial.

${\displaystyle V(r)=\frac{h^2}{2r^2{\sin }^2\theta }+gr\cos \theta }$

Para un valor dado de la energía ε el movimiento en la dirección radial tiene lugar entre las distancias r₁ y r₂ dados por las soluciones de la ecuación

${\displaystyle \epsilon =\frac{h^2}{2r^2{\sin }^2\theta }+gr\cos \theta }$

theta=pi/3; %ángulo del cono
h2=4; %cuadrado del momento angular Lz
energia=10; %energía
%energia potencial
f=@(r) h2/(2*r^2*sin(theta)^2)+9.8*r*cos(theta);
fplot(f,[0.2,3],'color','r')
ylim([0,20])
line([0,3],[energia,energia],'color','k')

%raíces
g=@(r) f(r)-energia;
r1=fzero(g,0.4);
r2=fzero(g,2);
line([r1,r1],[0,energia], 'lineStyle','--')
line([r2,r2],[0,energia],'lineStyle','--')
grid on
xlabel('r')
ylabel('V(r)')
title('Energía potencial')

En vez de utilizar fzero, buscamos las raíces de la ecuación cúbica

${\displaystyle r^3-\frac{\epsilon }{g\cos \theta }{r}^2+\frac{h^2}{2g{\sin }^2\theta \cos \theta }=0}$

>> a=-energia/(9.8*cos(theta));
>> c=h2/(2*9.8*sin(theta)^2*cos(theta));
>> raices_3([1,a,0,c])
ans =
   -0.4659
    1.8882
    0.6186

De las tres raíces reales dos son positivas r₁ y r₂ y una es negativa.

El mínimo de V(r) corresponde a una trayectoria circular de radio r₀.

${\displaystyle \begin{array}{l}\frac{dV(r)}{dr}=0\\ -\frac{h^2}{r_0^3{\sin }^2\theta }+g\cos \theta =0\end{array}}$

Conocido el momento angular h, despejamos el radio de la trayectoria circular r₀

De la constancia del momento angular h, obtenemos la velocidad angular dφ/dt constante de la partícula

${\displaystyle \begin{array}{l}h=r_0^2{\sin }^2\theta \left(\frac{d\phi }{dt}\right)\\ \frac{d\phi }{dt}=\frac{g\cos \theta }{r_0{\sin }^2\theta }\end{array}}$

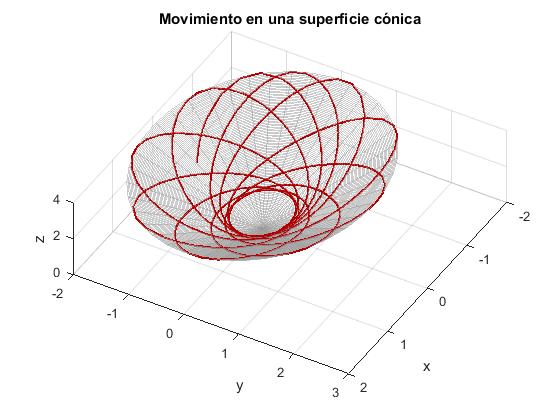
Trayectoria sobre la superficie cónica

Para representar la trayectoria seguida por la partícula, partimos de la posición r=r₁ en el que se cumple que dr/dt=0, establecemos φ=0. Determinamos la constante h a partir de los datos de r₁ y r₂. Igualando V(r₁)=V(r₂) obtenemos

${\displaystyle \begin{array}{l}\epsilon =\frac{h^2}{2r_1^2{\sin }^2\theta }+g{r}_1\cos \theta =\frac{h^2}{2r_2^2{\sin }^2\theta }+g{r}_2\cos \theta \\ h^2=2g\frac{r_1^2{r}_2^2}{r_1+r_2}{\sin }^2\theta \cos \theta \end{array}}$

Integramos las dos ecuaciones diferenciales con las condiciones iniciales señaladas para obtener la trayectoria r=r(φ) en la superficie cónica

${\displaystyle \begin{array}{l}\frac{d^{2}r}{d{t}^2}-\frac{h^2}{r^3{\sin }^2\theta }+g\cos \theta =0\\ r^2{\sin }^2\theta \frac{d\phi }{dt}=h\end{array}}$

r1=1;
r2=4; %radios mínimo y máximo
theta=pi/6; %ángulo del cono
%cuadrado del moemnto angular Lz
h2=2*9.8*r1^2*r2^2*sin(theta)^2*cos(theta)/(r1+r2); 
x0=[r1,0,0]; %condiciones iniciales
tspan=[0,20];
% x(1)=r, x(2)=dr/dt,x(3)=phi
fg=@(t,x)[x(2); h2/(x(1)^3*sin(theta)^2)-9.8*cos(theta); 
sqrt(h2)/(x(1)^2*sin(theta)^2)];
[t,x]=ode45(fg,tspan,x0);
xp=x(:,1).*cos(x(:,3))*sin(theta);
yp=x(:,1).*sin(x(:,3))*sin(theta);
zp=x(:,1)*cos(theta);
 
hold on
view(120,70)
%superficie cónica
phi=linspace(0,2*pi,40);
r=linspace(0,4);
[phi,r]=meshgrid(phi,r);
x=r.*cos(phi)*sin(theta);
y=r.*sin(phi)*sin(theta);
z=r*cos(theta);
h1=mesh(x,y,z);
set(h1,'EdgeColor',[0.6,0.6,0.6], 'FaceAlpha',0.5,'EdgeAlpha',0.5)
 
%trayectoria
h1=line(xp,yp,zp);
set(h1,'Color',[.7,0,0],'LineWidth',1.5)
 
hold off
grid on
xlabel('x')
ylabel('y')
zlabel('z')
title('Movimiento en una superficie cónica')

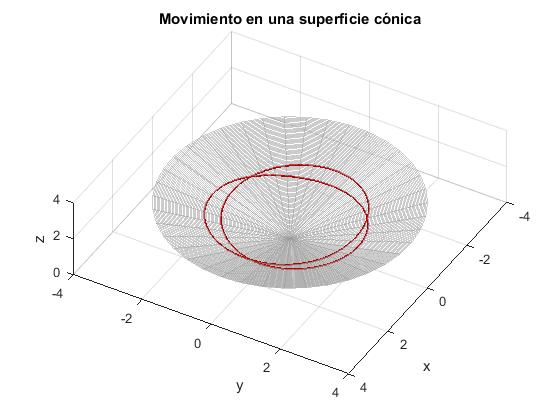
Trayectorias casi circulares

Para una trayectoria circular de radio r₀, la velocidad angular dφ/dt es constante

${\displaystyle \begin{array}{l}{h}^2=g{r}_0^3{\sin }^2\theta \cos \theta \\ \omega =\frac{d\phi }{dt}=\frac{h}{r_0^2{\sin }^2\theta }=\frac{1}{\sin \theta }\sqrt{\frac{g\cos \theta }{r_0}}\end{array}}$

Si el radio r de la trayectoria cambia muy poco con el tiempo, r=r₀+δ(t) . Aproximamos 1/r³

${\displaystyle \frac{1}{r^3}=\frac{1}{r_0^3}{\left(1+\frac{\delta }{r_0}\right)}^{-3}\approx \frac{1}{r_0^3}\left(1-3\frac{\delta }{r_0}\right)}$

>> syms x x0;
>> taylor(1/x^3,x,x0,'Order',2)
ans =1/x0^3 - (3*(x - x0))/x0^4

Introduciendo esta aproximación en la primera ecuación diferencial

${\displaystyle \begin{array}{l}\frac{d^2\delta }{d{t}^2}-\frac{h^2}{{\sin }^2\theta }\frac{1}{r_0^3}\left(1-3\frac{\delta }{r_0}\right)+g\cos \theta =0\\ \frac{d^2\delta }{d{t}^2}+\frac{3g\cos \theta }{r_0}\delta =0\end{array}}$

que corresponde a un Movimiento Armónico Simple de frecuencia angular Ω

${\displaystyle \Omega =\sqrt{\frac{3g\cos \theta }{r_0}}}$

El cociente Ω/ω es independiente de r₀

${\displaystyle \frac{\Omega }{\omega }=\sqrt{3}\sin \theta }$

La trayectoria es cerrada si este cociente es un número racional m/n. Por ejemplo, si θ=60° el cociente es 3/2. Para que el cociente sea 1/2 el ángulo θ=16.8°

Escribimos la aproximación r=r₀+δ(t)=r₀+ρcos(Ωt). Donde ρ<<r₀, es la amplitud

Conocida la expresión de r(t), obtenemos la expresión aproximada del ángulo φ(t), del siguiente modo

${\displaystyle \begin{array}{l}\frac{d\phi }{dt}=\frac{h}{r^2{\sin }^2\theta }=\frac{h}{r_0^2{\sin }^2\theta }{\left(1+\frac{\rho }{r_0}\cos (\Omega t)\right)}^{-2}\\ \frac{d\phi }{dt}\approx \omega {\left(1-2\frac{\rho }{r_0}\cos (\Omega t)\right)}^{-2}\\ \phi \approx \omega t-2\frac{\rho }{r_0}\frac{\omega }{\Omega }\sin (\Omega t)\end{array}}$

%r1=2;
%r2=2.5; %radios mínimo y máximo
r0=2.25;
theta=pi/3; % probar con asin(sqrt(3)/6);
w=sqrt(9.8*cos(theta)/r0)/sin(theta);
W=sqrt(3*9.8*cos(theta)/r0);
t=0:0.01:2*pi*W/w;
r=r0+0.25*sin(W*t);
phi=w*t-2*(0.25/r0)*(w/W)*sin(W*t);
xp=r.*cos(phi)*sin(theta);
yp=r.*sin(phi)*sin(theta);
zp=r*cos(theta);

hold on
view(120,70)
%superficie cónica
phi=linspace(0,2*pi,40);
r=linspace(0,4);
[phi,r]=meshgrid(phi,r);
x=r.*cos(phi)*sin(theta);
y=r.*sin(phi)*sin(theta);
z=r*cos(theta);
h1=mesh(x,y,z);
set(h1,'EdgeColor',[0.6,0.6,0.6], 'FaceAlpha',0.5,'EdgeAlpha',0.5)
 
%trayectoria
h1=line(xp,yp,zp);
set(h1,'Color',[.7,0,0],'LineWidth',1.5)
 
hold off
grid on
xlabel('x')
ylabel('y')
zlabel('z')
title('Movimiento en una superficie cónica')

Movimiento sobre la superficie de revolución, z=arⁿ

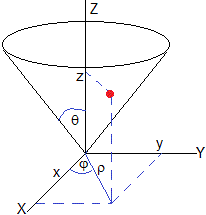
Consideremos una partícula de masa m que desliza sin rozamiento sobre la superficie de revolución, z=aρⁿ. Estableceremos coordenadas cilíndricas. El vector posición y el vector velocidad de la partícula se expresan

${\displaystyle \begin{array}{l}\overrightarrow{r}=\rho \widehat{\rho }+z\widehat{k}=\rho \widehat{\rho }+a{\rho }^n\widehat{k}\hfill \\ \overrightarrow{v}=\frac{d\rho }{dt}\widehat{\rho }+\rho \frac{d\phi }{dt}\widehat{\phi }+\frac{dz}{dt}\widehat{k}=\frac{d\rho }{dt}\widehat{\rho }+\rho \frac{d\phi }{dt}\widehat{\phi }+an{\rho }^{n-1}\frac{d\rho }{dt}\widehat{k}\hfill \end{array}}$

La energía cinética de la partícula es

${\displaystyle \begin{array}{l}T=\frac{1}{2}m{v}^2=\frac{1}{2}m\left({\left(\frac{d\rho }{dt}\right)}^2+{\rho }^2{\left(\frac{d\phi }{dt}\right)}^2+{\left(\frac{dz}{dt}\right)}^2\right)\\ T=\frac{1}{2}m\left(\left(1+n^2{\rho }^{2n-2}\right){\left(\frac{d\rho }{dt}\right)}^2+{\rho }^2{\left(\frac{d\phi }{dt}\right)}^2\right)\end{array}}$

La energía poptencial

${\displaystyle V=mgz=mg·a{\rho }^n}$

La lagrangiana

${\displaystyle L=T-V=\frac{1}{2}m\left(\left(1+n^2{\rho }^{2n-2}\right){\left(\frac{d\rho }{dt}\right)}^2+{\rho }^2{\left(\frac{d\phi }{dt}\right)}^2\right)-mg·a{\rho }^n}$

La ecuación del movimiento en la dirección radial, \widehat{\rho }

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\rho }}\right)-\frac{\partial L}{\partial \rho }=0\\ m\frac{d}{dt}\left(\left(1+n^2{\rho }^{2n-2}\right)\left(\frac{d\rho }{dt}\right)\right)-m{n}^2\left(n-1\right){\rho }^{2n-3}{\left(\frac{d\rho }{dt}\right)}^2-m\rho {\left(\frac{d\phi }{dt}\right)}^2+mgan{\rho }^{n-1}=0\\ n^2\left(2n-2\right){\rho }^{2n-3}{\left(\frac{d\rho }{dt}\right)}^2+\left(1+n^2{\rho }^{2n-2}\right)\frac{d^2\rho }{d{t}^2}-n^2\left(n-1\right){\rho }^{2n-3}{\left(\frac{d\rho }{dt}\right)}^2-\rho {\left(\frac{d\phi }{dt}\right)}^2+gan{\rho }^{n-1}=0\\ \left(1+n^2{\rho }^{2n-2}\right)\frac{d^2\rho }{d{t}^2}+n^2\left(n-1\right){\rho }^{2n-3}{\left(\frac{d\rho }{dt}\right)}^2-\rho {\left(\frac{d\phi }{dt}\right)}^2+gan{\rho }^{n-1}=0\end{array}}$

La ecuación del movimiento en la dirección angular, \widehat{\phi }

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\phi }}\right)-\frac{\partial L}{\partial \phi }=0\\ m\frac{d}{dt}\left({\rho }^2\frac{d\phi }{dt}\right)=0\\ {\rho }^2\frac{d\phi }{dt}=h\end{array}}$

Energía

Hay una cantidad que se conserva, la componente L_z=mh del momento angular, la otra es la energia E de la partícula

${\displaystyle \begin{array}{l}E=\frac{1}{2}m\left(\left(1+n^2{\rho }^{2n-2}\right){\left(\frac{d\rho }{dt}\right)}^2+{\rho }^2{\left(\frac{d\phi }{dt}\right)}^2\right)+mga{\rho }^n\\ E=\frac{1}{2}m\left(\left(1+n^2{\rho }^{2n-2}\right){\left(\frac{d\rho }{dt}\right)}^2+\frac{h^2}{{\rho }^2}\right)+mga{\rho }^n\end{array}}$

La energía potencial efectiva es

${\displaystyle V(\rho )=\frac{1}{2}m\frac{h^2}{{\rho }^2}+mg·a{\rho }^n}$

Representamos la energía potencial efectiva para n=2 y h=2

a=1;
n=2; %exponente
h=2; %momento angular
E=11.8; %energía
f=@(x) h^2./(2*x.^2)+9.8*a*x.^n;
fplot(f, [0.1,1.2])
line([0,1.2],[E,E])
line([1,1],[0,E],'lineStyle','--')
line([0.4518,0.4518],[0,E],'lineStyle','--')
hold on
grid on
ylim([0,15])
xlabel('\rho')
ylabel('V(\rho)')
title('Energía potencial efectiva')

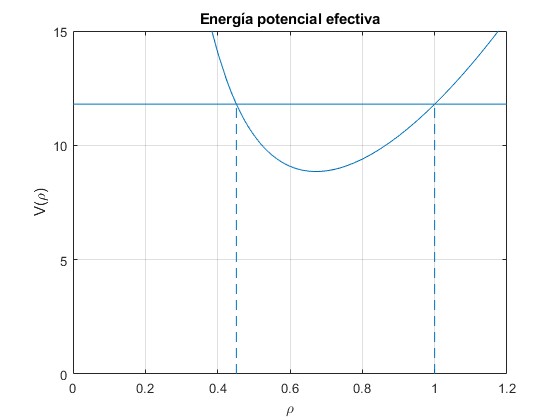
Supongamos que la partícula parte del reposo desde ρ₀=1 m, la energía inicial vale

${\displaystyle E=\frac{1}{2}m\frac{h^2}{{\rho }_0^2}+mga{\rho }_0^n,\frac{E}{m}=\frac{1}{2}\frac{2^2}{1^2}+9.8·1·1^2=11.8\text{J}}$

La energía en la posición inferior de retorno, dρ/dt=0

${\displaystyle \begin{array}{l}E=\frac{1}{2}m\frac{h^2}{{\rho }_1^2}+mga{\rho }_1^n,\frac{E}{m}=\frac{1}{2}\frac{2^2}{{\rho }_1^2}+9.8·1{\rho }_1^n\\ 9.8x^4-11.8x^2+2=0\end{array}}$

Una raíz de la ecuación bicuadrada es ρ₁=1 m, la otra ρ₁=0.4518 m tal como se aprecia en la figura anterior, la altura $z_1=a{\rho }_1^2=0.2041\text{m}$

>> x2=(11.8-sqrt(11.8^2-4*9.8*2))/(2*9.8)
x2 =    0.2041
>> r1=sqrt(x2)
r1 =    0.4518
>> z1=r1^2
z1 =    0.2041

Trayectorias

Resolvemos el sistema de dos ecuaciones diferenciales por el procedimiento ode45 de MATLAB

${\displaystyle \{\begin{array}{l}\left(1+n^2{\rho }^{2n-2}\right)\frac{d^2\rho }{d{t}^2}+n^2\left(n-1\right){\rho }^{2n-3}{\left(\frac{d\rho }{dt}\right)}^2-\frac{h^2}{{\rho }^3}+gan{\rho }^{n-1}=0\\ {\rho }^2\frac{d\phi }{dt}=h\end{array}}$

Tomamos a=1. Dado el valor del exponente n, fijamos el momento angular h. Las condiciones iniciales son, t=0, la posición inicial ρ=1, φ=0. La velocidad inicial dρ/dt=0 (parte del reposo)

Fijamos el valor del exponente n=2. Representamos la altura z de la partícula para varios valores del momento angular h.

a=1;
n=2; %exponente
hold on
% x(1)=r, x(2)=dr/dt,x(3)=phi
for h=[0.5,2,3]
    fg=@(t,x)[x(2);(h^2/x(1)^3-9.8*a*n*x(1)^(n-1)-n^2*(n-1)*x(1)^(2*n-3)*x(2)^2)
/(1+n^2*x(1)^(2*n-2)); h/x(1)^2];
    [t,x]=ode45(fg,[0,2],[1,0,0]);
    z=a*x(:,1).^n;
    plot(t, z,'displayName',num2str(h))
end 
hold off
grid on
xlabel('t')
legend('-DynamicLegend','location','best')
ylabel('z')
title('Movimiento en una superficie')

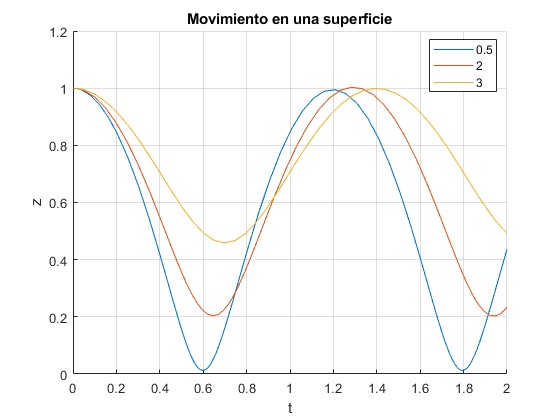
Hemos calculado la altura de la posición de retorno para h=2, z₁=0.2041 m, que se alcanza en el instante t≈0.65 s, tal como se aprecia en la figura

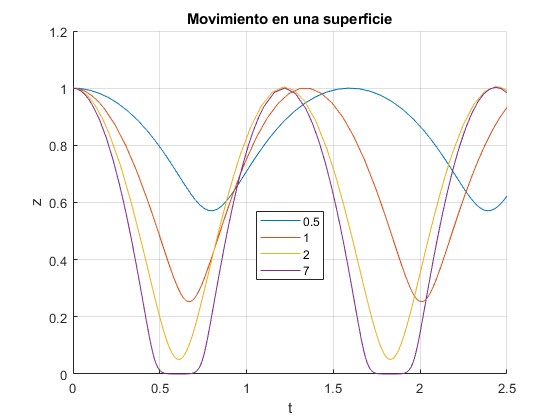
Fijamos el valor del momento angular h. Representamos la altura z de la partícula para varios valores del exponente n.

a=1;
h=1; %momento angular
hold on
% x(1)=r, x(2)=dr/dt,x(3)=phi
for n=[0.5,1,2,7]
    fg=@(t,x)[x(2);(h^2/x(1)^3-9.8*a*n*x(1)^(n-1)-n^2*(n-1)*x(1)^(2*n-3)*x(2)^2)
/(1+n^2*x(1)^(2*n-2)); h/x(1)^2];
    [t,x]=ode45(fg,[0,2.5],[1,0,0]);
    z=a*x(:,1).^n;
    plot(t, z,'displayName',num2str(n))
end 
hold off
grid on
xlabel('t')
legend('-DynamicLegend','location','best')
ylabel('z')
title('Movimiento en una superficie')

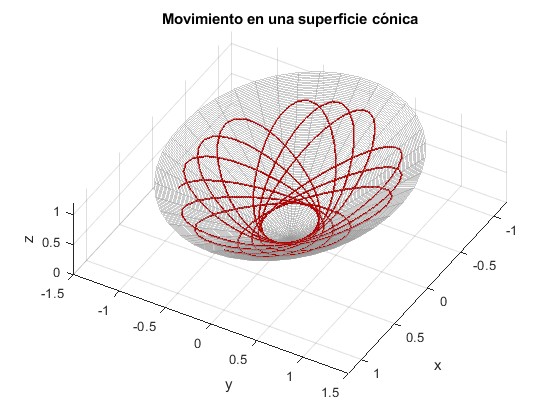
Representamos la trayectoria de una partícula que desliza sin rozamiento sobre la superficie de revolución con n=2 y h=1

a=1;
n=2; %exponente
h=1; %momento angular
% x(1)=r, x(2)=dr/dt,x(3)=phi
fg=@(t,x)[x(2);(h^2/x(1)^3-9.8*a*n*x(1)^(n-1)-n^2*(n-1)*x(1)^(2*n-3)*x(2)^2)
/(1+n^2*x(1)^(2*n-2)); h/x(1)^2];
[t,x]=ode45(fg,[0,20],[1,0,0]);
xp=x(:,1).*cos(x(:,3));
yp=x(:,1).*sin(x(:,3));
zp=a*x(:,1).^n;
 
 %energía
%E=((1+n^2*x(:,1).^(2*n-2)).*x(:,2).^2+h^2./x(:,1).^2)/2+9.8*a*x(:,1).^n;
hold on
%superficie cónica
phi=linspace(0,2*pi,40);
r=linspace(0,1.2);
[phi,r]=meshgrid(phi,r);
x=r.*cos(phi);
y=r.*sin(phi);
z=a*r.^n;
h1=mesh(x,y,z);
set(h1,'EdgeColor',[0.6,0.6,0.6], 'FaceAlpha',0.5,'EdgeAlpha',0.5)
 
%trayectoria
h1=line(xp,yp,zp);
set(h1,'Color',[.7,0,0],'LineWidth',1.5)
 
hold off
grid on
xlabel('x')
ylabel('y')
zlabel('z')
title('Movimiento en una superficie cónica')
view(120,70)

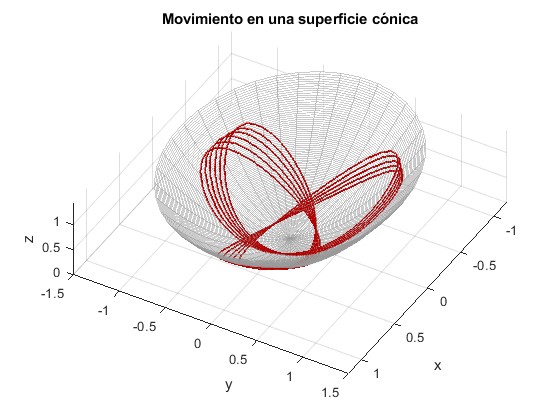
Representamos la trayectoria de la partícula para n=1/2

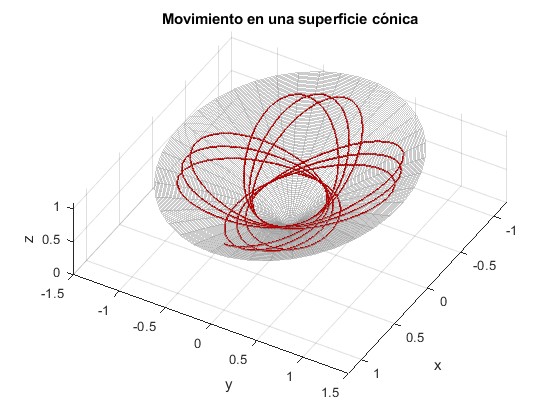
Representamos la trayectoria de la partícula para n=1, un superficie cónica

Referencias

Ricardo López-Ruiz, Amalio F Pacheco Sliding on the inside of a conical surface, Eur. J. Phys. 23 (2002) 579-589

D. G. Gómez-Pérez, O. González-Amezcua. The motion of a particle on the surface of a general cone. Revista Mexicana de Física E 21 010206 1–5. January-June 2024