La distancia más corta entre dos puntos

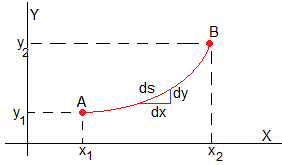
El problema más sencillo de cálculo de variaciones consiste en encontrar el camino más corto que une los puntos A(x₁,y₁) y B(x₂,y₂). Conocemos la respuesta que es el segmento de la recta que pasa por dichos puntos

Para cada intervalo dx a lo largo del eje X le corresponde un trozo de camino de longitud ds. Utilizando el teorema de Pitágoras

${\displaystyle ds=\sqrt{d{x}^2+d{y}^2}=\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}dx=\left(\sqrt{1+{\dot{y}}^2}\right)dx}$

Tenemos que encontrar el camino más corto y=y(x) entre los puntos A y B tal que la longitud de la trayectoria (la integral)

${\displaystyle I(y)={\displaystyle \underset{x_1}{\overset{x_2}{\int }}\sqrt{1+{\dot{y}}^2}}dx}$

sea mínima, con las condiciones de contorno

${\displaystyle \{\begin{array}{l}y(x_1)=y_1\\ y(x_2)=y_2\end{array}}$

La función, $f(x,y,\dot{y})=\sqrt{1+{\dot{y}}^2}$, no depende de x e y. Aplicando la ecuación de Euler-Lagrange

${\displaystyle \begin{array}{l}\frac{\partial f}{\partial \dot{y}}=\frac{\dot{y}}{\sqrt{1+{\dot{y}}^2}}\\ \frac{\dot{y}}{\sqrt{1+{\dot{y}}^2}}=C\end{array}}$

La solución es

${\displaystyle \begin{array}{l}{C}^2+C^2{\dot{y}}^2={\dot{y}}^2\\ \dot{y}=m\\ \frac{dy}{dx}=m\\ {\displaystyle \int dy}=m{\displaystyle \int dx}+C_1\\ y=mx+C_1\end{array}}$

Que es la ecuación de una recta. Calculamos la constante C₁ sabiendo que la recta pasa por A(x₁,y₁)

C₁=y₁-m·x₁

La ecuación de la recta es

y-y₁=m(x-x₁)

Calculamos la constante m (pendiente de la recta) sabiendo que la recta pasa por B(x₂,y₂)

${\displaystyle y=\frac{y_2-y_1}{x_2-x_1}\left(x-x_1\right)+y_1}$

Forma de un cuerpo que se mueve en un fluido, para que presente una resistencia mínima

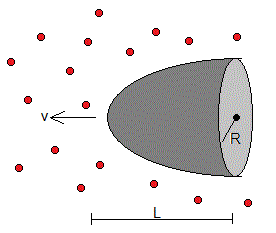
Consideremos un sólido de revolución que se mueve con velocidad v a través de un gas rarificado en el espacio exterior. Deseamos conocer la forma del cuerpo, es decir, la función y=y(x) que al girar alrededor del eje X genera la superficie de revolución, de modo que su resistencia al movimiento a través del gas sea mínima

Choque de una molécula contra el cuerpo

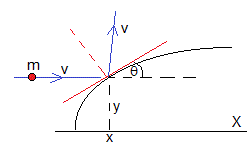
Nos situamos en el sistema de referencia que se mueve con el cuerpo. Una molécula de gas de masa m y velocidad v paralela al eje X choca con el cuerpo en la posición de abscisa x. El ángulo que forma la recta tangente a curva y=y(x) en x es tanθ=dy/dx.

Después del choque la partícula se refleja, (supondremos que la masa del cuerpo es mucho mayor que la masa m de la molécula). El ángulo que forma el vector v después del choque con el eje X es 2θ.

El cambio de momento lineal a lo largo del eje X es mvcos(2θ)-mv. El cuerpo ejerce una fuerza dirigida a la izquierda sobre la molécula para que cambie la dirección de su velocidad. La molécula ejerce sobre el cuerpo una fuerza igual y de sentido contrario, dirigida hacia la derecha. Este es el origen de la fuerza de resistencia que experimenta un cuerpo cuando se mueve a través de un gas

${\displaystyle \Delta p=mv\cos \left(2\theta \right)-mv=-2mv{\sin }^2\theta }$

Flujo de moléculas

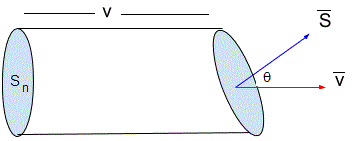
Supongamos que todas las moléculas se mueven con la misma velocidad v. Se denomina flujo al número de partículas que atraviesan la sección normal S_n en la unidad de tiempo, que es el producto del número n de partículas por unidad de volumen, por la velocidad v de las partículas y por el área de la sección normal S_n.

n·v·S_n

Si la superficie S está inclinada formando un ángulo θ, el flujo será

n·v·Scosθ, el producto escalar $n\overrightarrow{v}\overrightarrow{·S}$

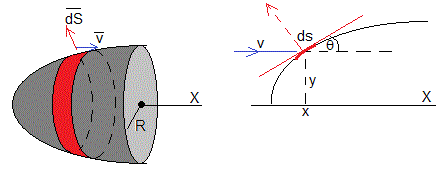
Consideremos el elemento dS de superficie de revolución marcado en color rojo en la figura. Su área es, dS=2πy·ds, siendo ds el elemento de arco

${\displaystyle ds=\sqrt{d{x}^2+d{y}^2}=\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}dx}$

El flujo de moléculas a través de este elemento de superficie es

${\displaystyle n\overrightarrow{v}·\overrightarrow{dS}=nv\left(2\pi y·ds\right)\cos \left(90+\theta \right)=-2\pi nvy·ds·\sin \theta }$

El cambio de momento lineal de las moléculas que chocan con este elemento de superficie, en la unidad de tiempo, es

${\displaystyle -2\pi nvy·ds·\sin \theta \left(-2mv{\sin }^2\theta \right)=4\pi nm{v}^{2}y{\sin }^3\theta ·ds}$

La densidad ρ del gas es la masa por unidad de volumen, o el producto del número de moléculas n por unidad de volumen por la masa m de cada molécula, ρ=m·n

Recordando que tanθ=dy/dx, y

${\displaystyle \sin \theta =\frac{\tan \theta }{\sqrt{1+{\tan }^2\theta }}\sin \theta =\frac{\dot{y}}{\sqrt{1+{\dot{y}}^2}}}$

La fuerza F que ejerce el cuerpo sobre las moléculas es el cambio de momento lineal de todas las moléculas que chocan con su superficie de revolución en la unidad de tiempo

${\displaystyle \begin{array}{l}F=4\pi \rho v^2{\displaystyle \underset{0}{\overset{L}{\int }}y{\sin }^3\theta ·ds}\\ F=4\pi \rho v^2{\displaystyle \underset{0}{\overset{L}{\int }}y{\left(\frac{\dot{y}}{\sqrt{1+{\dot{y}}^2}}\right)}^3}\sqrt{1+{\dot{y}}^2}dx\\ F(y)=4\pi \rho v^2{\displaystyle \underset{0}{\overset{L}{\int }}\frac{y{\dot{y}}^3}{1+{\dot{y}}^2}}dx\end{array}}$

El problema consiste en hallar la función y(x) en la que F alcanza su valor menor posible siendo y(0)=0 e y(L)=R. Dado que la función

${\displaystyle f(x,y,\dot{y})=\frac{y{\dot{y}}^3}{1+{\dot{y}}^2}}$

no depende de x, la ecuación de Euler-Lagrange se escribe

${\displaystyle \begin{array}{l}f-\dot{y}\frac{\partial f}{\partial \dot{y}}=C_1\\ \frac{{\dot{y}}^{3}y}{{\left(1+{\dot{y}}^2\right)}^2}=C_1\end{array}}$

Despejamos dy/dx, obteniendo la ecuación diferencial

${\displaystyle C_1{\left(\frac{dy}{dx}\right)}^4-y{\left(\frac{dy}{dx}\right)}^3+2C_1{\left(\frac{dy}{dx}\right)}^2+C_1=0}$

Si hacemos la aproximación (dy/dx)²<<1, la ecuación diferencial se puede resolver fácilmente

${\displaystyle \begin{array}{l}y{\left(\frac{dy}{dx}\right)}^3=C_1\\ {\displaystyle \int y^{1/3}dy=C_1{\displaystyle \int dx+C_2}}\\ y^{4/3}=C_{1}x+C_2\\ y={\left(C_{1}x+C_2\right)}^{3/4}\end{array}}$

Las constantes C₁ y C₂ se determinan a partir de las condiciones de contorno: x=0, y=0, C₂=0; x=L, y=R, C₁=R^4/3/L

${\displaystyle y=R{\left(\frac{x}{L}\right)}^{3/4}}$

Máxima intensidad del campo gravitatorio

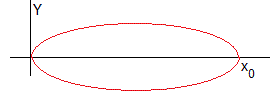
Un asteroide tiene la forma de una superficie de revolución generada por la función y=y(x), cuando gira alrededor del eje X, su longitud es x₀

Queremos determinar dicha función para que la intensidad del campo gravitatorio en el origen O, producido por esta distribución de masa de densidad constante ρ, sea máxima

Procedemos a calcular la intensidad del campo gravitatorio en O, siguiendo los mismos pasos que en la página titulada La aceleración de la gravedad en el interior y en el exterior de una distribución esférica y uniforme de masa

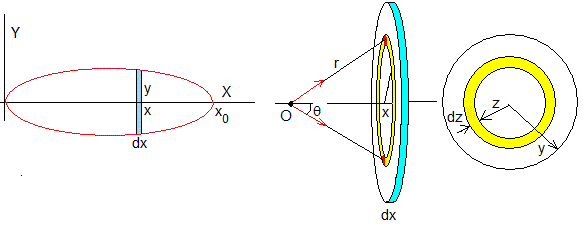
Dividimos el asteroide en discos de espesor dx. Consideremos el que está comprendido entre x y x+dx.

En este disco, tomamos un elemento diferencial de masa de radio z y espesor dz que dista r del origen. Su masa es dm=ρ(2πz·dz)dx

El módulo de la aceleración de la gravedad en el origen es

${\displaystyle G\frac{dm}{r^2}=G\frac{\rho \left(2\pi z·dz\right)dx}{r^2}}$

Su dirección es la recta que une el origen O y el elemento diferencial de masa. Su componente horizontal (a lo largo del eje X) es

${\displaystyle G\frac{dm}{r^2}\cos \theta =G\frac{\rho \left(2\pi z·dz\right)dx}{r^2}\frac{x}{r}=G\frac{2\pi \rho x·z}{{\left(x^2+z^2\right)}^{3/2}}dz·dx}$

Las componentes perpendiculares (al eje X) se anulan por simetría

Integramos con respecto a z entre 0 e y, para calcular la aceleración de la gravedad producida por el disco en O

${\displaystyle {\displaystyle \underset{0}{\overset{y}{\int }}G\frac{2\pi \rho x·z}{{\left(x^2+z^2\right)}^{3/2}}dz·dx}=G\left(2\pi \rho x·dx\right){\displaystyle \underset{0}{\overset{y}{\int }}\frac{z}{{\left(x^2+z^2\right)}^{3/2}}dz}=G\left(2\pi \rho x·dx\right)\left(\frac{1}{x}-\frac{1}{\sqrt{x^2+y^2}}\right)}$

Calculamos la aceleración de la gravedad producida por el asteroide sumando la de todos los discos comprendidos entre 0 y x₀

${\displaystyle g_0={\displaystyle \underset{0}{\overset{x_0}{\int }}G\left(2\pi \rho x\right)\left(\frac{1}{x}-\frac{1}{\sqrt{x^2+y^2}}\right)}·dx=2\pi \rho G{\displaystyle \underset{0}{\overset{x_0}{\int }}\left(1-\frac{x}{\sqrt{x^2+y^2}}\right)dx}}$

El volumen V del asteroide, es la suma de los volúmenes de los discos

${\displaystyle V={\displaystyle \underset{0}{\overset{x_0}{\int }}\pi y^2·dx}}$

Vamos a resolver este problema de extremo condicionado. Formamos la función auxiliar, dependiente de un parámetro λ

${\displaystyle F(x,y,\dot{y})=1-\frac{x}{\sqrt{x^2+y^2}}+\lambda y^2}$

Aplicamos la ecuación Euler-Lagrange

${\displaystyle \frac{\partial F}{\partial y}-\frac{d}{dx}\left(\frac{\partial F}{\partial \dot{y}}\right)=0}$

La función F no depende de $\dot{y}$, la derivada dy/dx

${\displaystyle \begin{array}{l}\frac{\partial F}{\partial y}=\frac{xy}{{\left(x^2+y^2\right)}^{3/2}}+2\lambda y=0\\ \frac{x}{{\left(x^2+y^2\right)}^{3/2}}+2\lambda =0\end{array}}$

Como la función y=y(x) se anula y=0 para x₀, en el otro extremo del asteroide

${\displaystyle \frac{1}{x_0^2}+2\lambda =0}$

Ahora obtenemos x₀ a partir del volumen V del asteroide

${\displaystyle \begin{array}{l}\frac{x}{{\left(x^2+y^2\right)}^{3/2}}=\frac{1}{x_0^2}\\ y^2=x_0^{4/3}{x}^{2/3}-x^2\\ V={\displaystyle \underset{0}{\overset{x_0}{\int }}\pi \left(x_0^{4/3}{x}^{2/3}-x^2\right)·dx}=\frac{4}{15}\pi x_0^3\end{array}}$

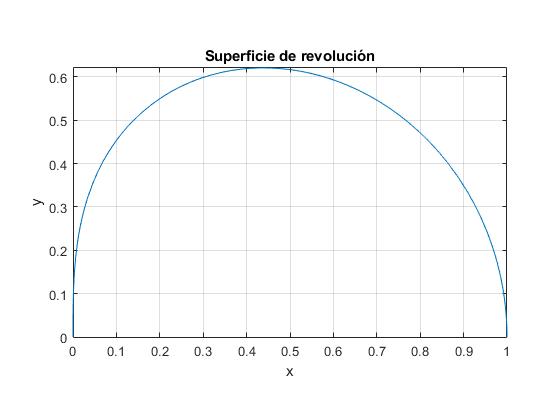
Representamos la función y=y(x) tomando x₀=1

fplot(@(x) sqrt(x.^(2/3)-x.^2),[0,1])
axis equal
grid on
xlabel('x')
ylabel('y')
title('Superficie de revolución')

Referencias

M. L. Krasnov, G. I. Makarenko, A. I. Kiseliov. Cálculo Variacional (ejemplos y problemas). Editorial Mir (1992)

Kirk T. McDonald. Maximal Gravity at the Surface of an Asteroid. https://www.physics.princeton.edu/~mcdonald/examples/