En esta página, estudiamos la braquistócrona en un campo eléctrico creado por una placa conductora conectada a tierra. Calculamos la trayectoria que ha de seguir una partícula cargada bajo la acción del campo eléctrico para que emplee un tiempo mínimo en recorrerla.

En el capítulo campo eléctrico estudiamos que el sistema formado por una carga positiva +q distante H-y de una placa plana e indefinida conectada a tierra es equivalente a un sistema formado por dos cargas +q y –q (carga imagen) separadas a una distancia 2(H-y).

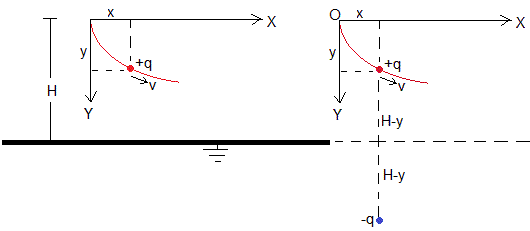
Supongamos que una partícula de masa m lleva una carga +q, parte del origen, situado a una altura H por encima de la placa horizontal, con velocidad nula, cuando se encuentra en la posición (x, y), su velocidad v se calcula aplicando el principio de conservación de la energía

${\displaystyle \begin{array}{l}\frac{1}{4\pi {\epsilon }_0}\frac{q^2}{2H}=\frac{1}{2}m{v}^2+\left(-\frac{1}{4\pi {\epsilon }_0}\frac{q^2}{2(H-y)}\right)\\ v^2=\frac{1}{4\pi {\epsilon }_0}\frac{q^2}{mH}\left(\frac{y}{H-y}\right)\end{array}}$

En términos de magnitudes adimendionales Y=y/H y X=x/H

${\displaystyle v=k\sqrt{\frac{Y}{1-Y}}}$

El tiempo que tarda la partícula en desplazarse desde el origen O hasta el punto P de coordenadas (x,y) es

${\displaystyle {\displaystyle \underset{O}{\overset{P}{\int }}dt=}{\displaystyle \underset{O}{\overset{P}{\int }}\frac{ds}{v}}={\displaystyle \underset{O}{\overset{P}{\int }}\frac{\sqrt{d{x}^2+d{y}^2}}{v}}=\frac{H}{k}{\displaystyle \underset{0}{\overset{X}{\int }}\sqrt{\frac{1-Y}{Y}\left\{{\left(\frac{dY}{dX}\right)}^2+1\right\}}dX}}$

Aplicando la ecuación de Euler-Lagrange a la función f

${\displaystyle \begin{array}{l}f(X,Y,\dot{Y})=\sqrt{\frac{1-Y}{Y}\left({\dot{Y}}^2+1\right)}\\ \frac{\partial f}{\partial X}-\frac{d}{dX}\left(f-\frac{\partial f}{\partial \dot{Y}}\dot{Y}\right)=0\end{array}}$

Dado que f no depende de X, el término entre paréntesis se mantiene constante. El resultado es

${\displaystyle \begin{array}{l}\sqrt{\frac{1-Y}{Y}\left({\dot{Y}}^2+1\right)}-\frac{2\dot{Y}\frac{1-Y}{Y}}{2\sqrt{\frac{1-Y}{Y}\left({\dot{Y}}^2+1\right)}}\dot{Y}=C\\ \frac{Y}{1-Y}\left({\dot{Y}}^2+1\right)=C\\ \frac{dY}{dX}=\sqrt{C\frac{1-Y}{Y}-1}\end{array}}$

Integramos

${\displaystyle {\displaystyle \int \sqrt{\frac{Y}{p-Y}}dY+C_1=X\sqrt{C+1}p=\frac{C}{C+1}}}$

Para resolver la integral hacemos el cambio de variable

${\displaystyle \begin{array}{l}Y=p{\sin }^2\theta \\ dY=2p\sin \theta \cos \theta ·d\theta \\ \int \sqrt{\frac{Y}{p-Y}}dY=2p\int \tan \theta \sin \theta \cos \theta ·d\theta =2p\int {\sin }^2\theta ·d\theta =p\int \left(1-\cos (2\theta )\right)d\theta =\\ p\left(\theta -\frac{1}{2}\sin (2\theta )\right)\end{array}}$

El resultado es

${\displaystyle p\left(\theta -\frac{1}{2}\sin (2\theta )\right)+C_1=X\sqrt{C+1}}$

Se determina la constante C₁ sabiendo que la trayectoria pasa por el origen (X=0, y=0). Teniendo en cuenta que Y=0, psin²θ=0, lo que implica que θ=0, por lo que C₁=0

${\displaystyle \begin{array}{l}X=\frac{p}{\sqrt{C+1}}\left(\theta -\frac{1}{2}\sin (2\theta )\right)\\ Y=p{\sin }^2\theta \\ Y=\frac{p}{2}\left(1-\cos (2\theta )\right)\end{array}}$

Llamando φ=2θ, escribimos las ecuaciones de la trayectoria dependientes del parámetro φ

${\displaystyle \begin{array}{l}X=\frac{C}{2{\left(C+1\right)}^{3/2}}\left(\phi -\sin \phi \right)\\ Y=\frac{C}{2(C+1)}\left(1-\cos \phi \right)\end{array}}$

El tiempo de viaje entre el origen, (0,0) o φ=0, y un punto (X, Y) o φ es

${\displaystyle T=\frac{H}{k}{\displaystyle \underset{0}{\overset{P}{\int }}\sqrt{\frac{1-Y}{Y}\left\{{\left(\frac{dY}{dX}\right)}^2+1\right\}}dX}}$

Teniendo en cuenta que

${\displaystyle \frac{dY}{dX}=\sqrt{(C+1)\frac{1+\cos \phi }{1-\cos \phi }}}$

Obtenemos

${\displaystyle \begin{array}{l}T=\frac{H}{k}\frac{\sqrt{C}}{2{\left(C+1\right)}^{3/2}}{\displaystyle \underset{0}{\overset{\phi }{\int }}(C+2+C\cos \phi )d\phi }\\ T=\frac{H}{k}\frac{\sqrt{C}}{2{\left(C+1\right)}^{3/2}}\left((C+2)\phi +C\sin \phi \right)\end{array}}$

Poniendo la constante C=2a/(1-2a), obtenemos las ecuaciones que aparecen en el artículo mencionado en las referencias

${\displaystyle \begin{array}{l}\{\begin{array}{l}X=a\sqrt{1-2a}\left(\phi -\sin \phi \right)\\ Y=a\left(1-\cos \phi \right)\end{array}\\ T=\frac{H}{k}\sqrt{2a}\left(\phi -a\phi +a\sin \phi \right)\end{array}}$

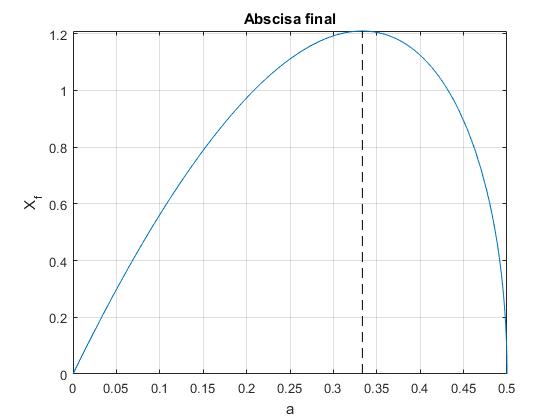
La constante a<1/2, para que la raíz cuadrada sea positiva. Cuando el parámetro φ=0, la partícula parte del origen (X=0, Y=0). Cuando φ=2π, la partícula regresa al eje X, Y_f=0, $X_f=2\pi a\sqrt{1-2a}$. X_f toma su valor máximo cuando

${\displaystyle \frac{d{X}_f}{da}=2\pi a\sqrt{1-2a}-\frac{2\pi a}{\sqrt{1-2a}}=0}$

La solución es a=1/3, lo que da el máximo valor de X_f=1.2092, tal como apreciamos en la figura

f=@(a) 2*pi*a.*sqrt(1-2*a);
fplot(f,[0,1/2])
line([1/3,1/3],[0,f(1/3)],'color','k','lineStyle','--')
grid on
xlabel('a')
ylabel('X_f')
title('Abscisa final')

Trayectorias

Representamos las trayectorias, para distintos valores de 1/3≤a<0.5

hold on
for a=1/3:1/60:1/2-1/60
    x=@(phi) a*sqrt(1-2*a)*(phi-sin(phi));
    y=@(phi) a*(1-cos(phi));
    fplot(x,y,[0,2*pi])
end

hold off
set (gca,'Ydir','reverse')
grid on
xlabel('X')
ylabel('Y')
title('Braquistocrona')

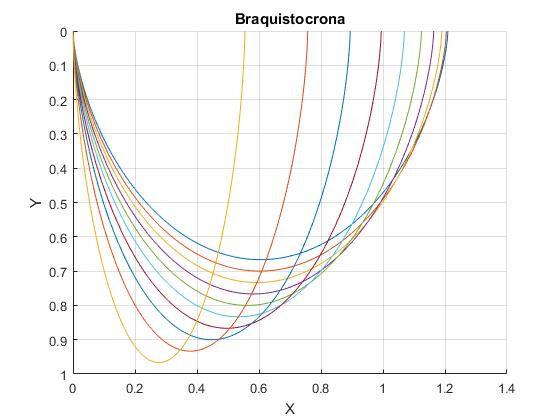
La figura muestra que hay dos posibles trayectorias que alcanzan el punto final (X_f, Y_f). Tenemos que resolver el sistema de dos ecuaciones no lineales

${\displaystyle \{\begin{array}{l}a\sqrt{1-2a}\left(\phi -\sin \phi \right)=X_f\\ a\left(1-\cos \phi \right)=Y_f\end{array}}$

Despejamos la constante a en la segunda ecuación y sustituimos en la primera, quedando la ecuación trascendente, f(φ)=0.

${\displaystyle \frac{Y_f}{1-\cos \phi }\sqrt{1-2\frac{Y_f}{1-\cos \phi }}\left(\phi -\sin \phi \right)-X_f=0}$

Representamos la función f(φ), para el punto X_f=0.4, Y_f=0.6, de este modo averiguaremos el valor aproximado de las raíces φ₁ y φ₂

X=0.4; %coordenadas del punto
Y=0.6;
f=@(x) Y*sqrt(1-2*Y./(1-cos(x))).*(x-sin(x))./(1-cos(x))-X;
fplot(f,[0,2*pi])
line([0,2*pi],[0,0],'color','k','lineStyle','--')
set(gca,'XTick',0:pi/2:2*pi)
set(gca,'XTickLabel',{'0','\pi/2','\pi','3\pi/2','2\pi'})
xlabel('\phi')
ylabel('f(\phi)')
title('Raíces')
%raíces
phi=fzero(f,2.6);
fprintf('constante ang=%1.4f, parámetro a=%1.4f\n',phi,Y/(1-cos(phi)));
phi=fzero(f,4.5);
fprintf('constante ang=%1.4f, parámetro a=%1.4f\n',phi,Y/(1-cos(phi)));

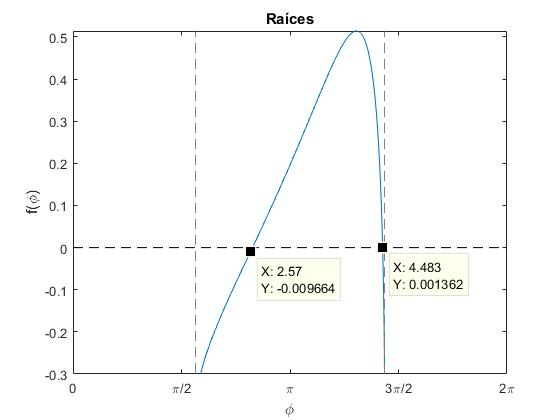
parámetro ang=2.5982, constante a=0.3233
parámetro ang=4.4828, constante a=0.4888

Trazamos las trayectorias hasta el punto

X=0.4; %coordenadas del punto
Y=0.6;
ang=[2.5982,4.4828];
hold on
i=1;
a=[0.3233,0.4888];
for p=a
    x=@(phi) p*sqrt(1-2*p)*(phi-sin(phi));
    y=@(phi) p*(1-cos(phi));
    fplot(x,y,[0,ang(i)])
    i=i+1;
end
plot(X,Y,'o','markersize',4,'markeredgecolor','k','markerfacecolor','k')
hold off
set (gca,'Ydir','reverse')
grid on
xlabel('X')
ylabel('Y')
title('Braquistocrona')

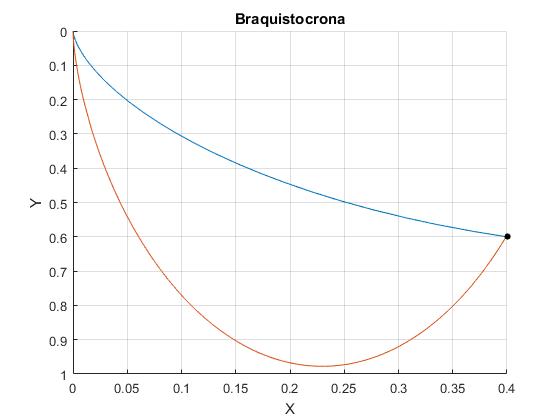
Finalmente, calculamos el tiempo que tarda la partícula en llegar al punto final, siguiendo una u otra trayectoria. Añadimos al script las siguientes líneas de código

for i=1:2
    T=sqrt(2*a(i))*(ang(i)-a(i)*ang(i)+a(i)*sin(ang(i)));
    fprintf('Tiempo %1.4f\n',T);
end

Tiempo 1.5482
Tiempo 1.7952

Se puede demostrar, véase el artículo mencionado en las referencias, que si a₁<a₂, entonces el tiempo T₁<T₂ que tarda la partícula en llegar al punto, (X,Y) siguiendo una u otra trayectoria

La envolvente

En la gráfica observamos que no todos los puntos del plano son alcanzados por las trayectorias, sino aquellos que están en el interior de una curva denominada envolvente

Para trazar la envolvente, escribimos la ecuación de la trayectoria, una función f(X,Y,φ). Para ello despejamos a=Y/(1-cosφ) de la segunda ecuación y la introducimos en la primera

${\displaystyle \begin{array}{l}X=\frac{Y}{1-\cos \phi }\sqrt{1-2\frac{Y}{1-\cos \phi }}\left(\phi -\sin \phi \right)\\ X=Y\frac{\phi -\sin \phi }{{\left(1-\cos \phi \right)}^{3/2}}\sqrt{1-\cos \phi -2Y}\end{array}}$

Derivamos la ecuación de la trayectoria f(X,Y,φ) con respecto al parámetro φ e igualamos a cero

${\displaystyle \begin{array}{l}\frac{\partial f}{\partial \phi }=0\\ \frac{\left(1-\cos \phi \right){\left(1-\cos \phi \right)}^{3/2}-\frac{3}{2}\sin \phi \sqrt{1-\cos \phi }\left(\phi -\sin \phi \right)}{{\left(1-\cos \phi \right)}^3}\sqrt{1-\cos \phi -2Y}+\\ \frac{\phi -\sin \phi }{{\left(1-\cos \phi \right)}^{3/2}}\frac{\sin \phi }{2\sqrt{1-\cos \phi -2Y}}=0\end{array}}$

Simplificando, despejamos Y

${\displaystyle \begin{array}{l}\frac{{\left(1-\cos \phi \right)}^2-\frac{3}{2}\sin \phi \left(\phi -\sin \phi \right)}{1-\cos \phi }\left(1-\cos \phi -2Y\right)+\frac{\left(\phi -\sin \phi \right)\sin \phi }{2}=0\\ Y=\frac{2-4\cos \phi -\phi \sin \phi +2{\cos }^2\phi +\phi \sin \phi \cos \phi }{4-4\cos \phi -3\phi \sin \phi +{\sin }^2\phi }\end{array}}$

Conocido Y, determinamos el valor la constante a

${\displaystyle a=\frac{2-4\cos \phi -\phi \sin \phi +2{\cos }^2\phi +\phi \sin \phi \cos \phi }{\left(1-\cos \phi \right)\left(4-4\cos \phi -3\phi \sin \phi +{\sin }^2\phi \right)}}$

Representamos a en función del parámetro φ comprendido entre (π, 2π). El valor mínimo de a es 1/3 y el máximo 1/2

a=@(phi) (2-4*cos(phi)-phi.*sin(phi)+2*cos(phi).^2+phi.*sin(phi).*cos(phi)).
/((1-cos(phi)).*(4-4*cos(phi)-3*phi.*sin(phi)+sin(phi).^2));
fplot(a,[pi,2*pi])
grid on
xlabel('\phi')
ylabel('a')
title('Constante a')

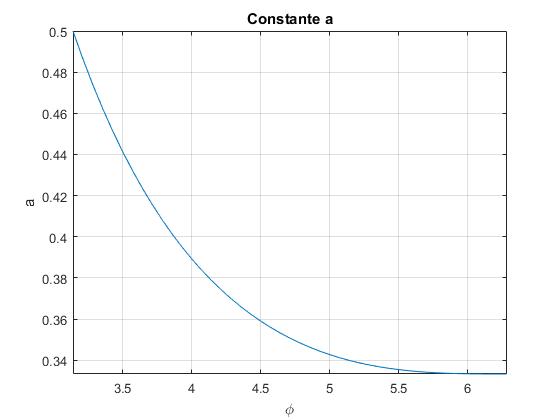
Conocido la constante a, utilizamos las ecuaciones paramétricas de la trayectoria para dibujar la envolvente

Completamos el primer script, añadiendo al trazado de las trayectorias, la envolvente, la curva de color rojo de la figura

hold on
for a=1/3:1/60:1/2-1/60
    x=@(phi) a*sqrt(1-2*a)*(phi-sin(phi));
    y=@(phi) a*(1-cos(phi));
    fplot(x,y,[0,2*pi],'color','b')
end
%envolvente
phi=pi:pi/180:2*pi;
a=(2-4*cos(phi)-phi.*sin(phi)+2*cos(phi).^2+phi.*sin(phi).*cos(phi)).
/((1-cos(phi)).*(4-4*cos(phi)-3*phi.*sin(phi)+sin(phi).^2));
x=a.*sqrt(1-2*a).*(phi-sin(phi));
y=a.*(1-cos(phi));
plot(x,y,'r')
hold off
set (gca,'Ydir','reverse')
grid on
xlabel('X')
ylabel('Y')
title('Braquistocrona')

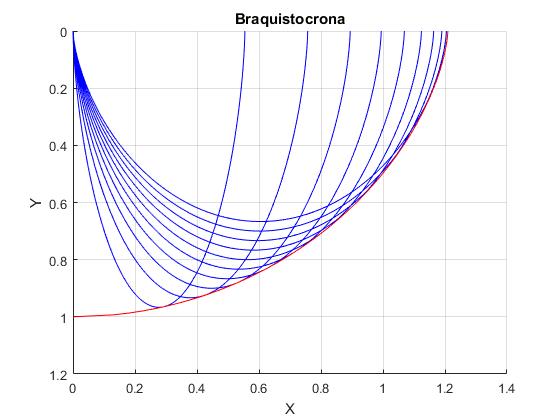
Referencias

Trevor C Lipscombe, Carl E Mungan. The electrobrachistrochrone, Eur. J. Phys. 39 (2018) 035006