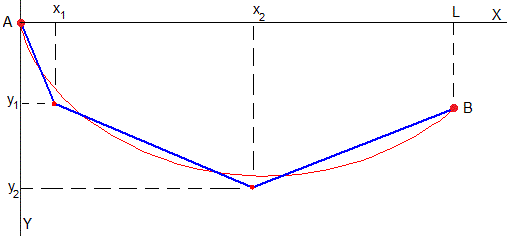
Conectamos dos puntos del plano A y B situados a distinta altura por un conjunto N de planos inclinados (en color azul). Una partícula parte del reposo del primer punto A y desliza sin rozamiento a lo largo de los planos inclinados hasta llegar al segundo punto B. Dependiendo de las coordenadas de los puntos (x_k, y_k), k=1,2,...N-1, que conectan las rampas, el tiempo que emplea la partícula en recorrerlas puede ser mayor o menor. Calcularemos las coordenadas de estos puntos cuando este tiempo sea mínimo y lo compararemos con el tiempo que le lleva a la partícula recorrer la trayectoria cicloidal (en color rojo) que une los puntos A y B.

Plano inclinado

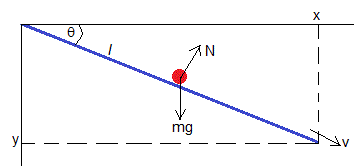
Consideremos un plano inclinado que une el origen con un punto de coordenadas (x, y). Si no hay rozamiento las fuerzas sobre la partícula son el peso mg y la reacción del plano inclinado, N=mgcosθ.

La aceleración del cuerpo es gsinθ=gy/l, siendo l la longitud del plano inclinado. La velocidad final v y el tiempo t que le lleva a la partícula recorrer el plano inclinado son

${\displaystyle \begin{array}{l}\{\begin{array}{l}v=g\sin \theta ·t\\ l=\frac{1}{2}g\sin \theta ·t^2\end{array}\\ t=\sqrt{\frac{2}{gy}}l\\ v=\sqrt{2gy}\end{array}}$

La velocidad final v solamente depende de la ordenada y del extremo del plano inclinado. Esta velocidad se puede obtener aplicando el principio de conservación de la energía

${\displaystyle mgy=\frac{1}{2}m{v}^2}$

Expresamos el tiempo t en términos de las coordenadas (x, y) del extremo del plano inclinado

${\displaystyle t=2\frac{\sqrt{x^2+y^2}}{\sqrt{2gy}}}$

Consideremos ahora una rampa que conecta dos puntos (x_k, y_k) y (x_k+1, y_k+1)

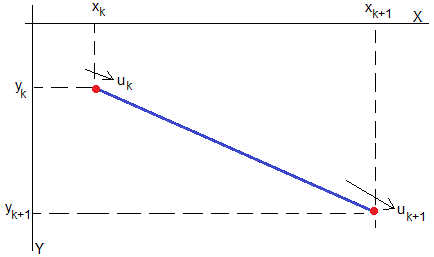
La velocidad inicial u_k y la final u_k+1 solamente dependen de las ordenadas de los extremos, y_k e y_k+1

${\displaystyle \begin{array}{l}{u}_k=\sqrt{2g{y}_k}\\ u_{k+1}=\sqrt{2g{y}_{k+1}}\end{array}}$

Calculamos el tiempo t_k que le lleva a la partícula recorrer el plano inclinado k de longitud l_k

${\displaystyle \begin{array}{l}\{\begin{array}{l}{u}_{k+1}=u_k+g\sin \theta ·t_k\\ l_k=u_{k}t+\frac{1}{2}g\sin \theta ·t_k^2\end{array}\\ l_k=\frac{u_{k+1}+u_k}{2}{t}_k\\ t_k=2\frac{\sqrt{{\left(x_{k+1}-x_k\right)}^2+{\left(y_{k+1}-y_k\right)}^2}}{\sqrt{2g{y}_{k+1}}+\sqrt{2g{y}_k}}\end{array}}$

Cuando la aceleración es constante, la velocidad media de la partícula en el plano inclinado es v_k=(u_k+u_k+1)/2 es la media de sus velocidades en los extremos. El tiempo t_k es el cociente entre la longitud l_k del plano inclinado y la velocidad media v_k

El tiempo total t que tarda en desplazarse la partícula de A (0,0) y B (L, H) a través de N rampas es

${\displaystyle t=\frac{2}{\sqrt{2g}}\left\{\frac{\sqrt{x_1^2+y_1^2}}{\sqrt{y_1}}+\mathrm{...}\frac{\sqrt{{\left(x_{k+1}-x_k\right)}^2+{\left(y_{k+1}-y_k\right)}^2}}{\sqrt{y_{k+1}}+\sqrt{y_k}}+\mathrm{...}+\frac{\sqrt{{\left(L-x_{N-1}\right)}^2+{\left(H-y_{N-1}\right)}^2}}{\sqrt{y_{N-1}}+\sqrt{H}}\right\}}$

Definimos nuevas variables adimensionales X=x/H, Y=y/H y $T=\frac{t}{\sqrt{\frac{2H}{g}}}$

${\displaystyle T=\frac{\sqrt{X_1^2+Y_1^2}}{\sqrt{Y_1}}+\mathrm{...}\frac{\sqrt{{\left(X_{k+1}-X_k\right)}^2+{\left(Y_{k+1}-Y_k\right)}^2}}{\sqrt{Y_{k+1}}+\sqrt{Y_k}}+\mathrm{...}+\frac{\sqrt{{\left(\frac{L}{H}-X_{N-1}\right)}^2+{\left(1-Y_{N-1}\right)}^2}}{\sqrt{Y_{N-1}}+1}}$

Dos rampas

Unimos los puntos A (0,0) y B (L, H), mediante dos rampas. El tiempo T que emplea la partícula en desplazarse sin rozamiento a lo largo de este camino, partiendo de A en reposo es

${\displaystyle T=\frac{\sqrt{X_1^2+Y_1^2}}{\sqrt{Y_1}}+\frac{\sqrt{{\left(\frac{L}{H}-X_1\right)}^2+{\left(1-Y_1\right)}^2}}{\sqrt{Y_1}+1}}$

Para que T sea mínimo se tiene que cumplir que

${\displaystyle \frac{\partial T}{\partial X_1}=\mathrm{0,}\frac{\partial T}{\partial Y_1}=0}$

Obtenemos un sistema no lineal de dos ecuaciones con dos incógnitas

${\displaystyle \begin{array}{l}\frac{X_1}{\sqrt{X_1^2+Y_1^2}\sqrt{Y_1}}-\frac{\left(L/H-X_1\right)}{\sqrt{{\left(L/H-X_1\right)}^2+{\left(1-Y_1\right)}^2}\left(\sqrt{Y_1}+1\right)}=0\\ -\frac{{\left(X_1-Y_1\right)}^2}{Y_1\sqrt{Y_1}\sqrt{X_1^2+Y_1^2}}-\frac{2\left(1-Y_1\right)\left(\sqrt{Y_1}+1\right)\sqrt{Y_1}+{\left(L/H-X_1\right)}^2+{\left(1-Y_1\right)}^2}{{\left(\sqrt{Y_1}+1\right)}^2\sqrt{Y_1}\sqrt{{\left(L/H-X_1\right)}^2+{\left(1-Y_1\right)}^2}}=0\end{array}}$

Intentamos resolver este sistema no lineal mediante fsolve de MATLAB para L=5 y H=1, recibimos un aviso y vemos que no lo resuelve satisfactoriamente

L=5;
H=1;
f=@(x) [x(1)/(sqrt(x(1)^2+x(2)^2)*sqrt(x(2)))-(L/H-x(1))/
(sqrt((L/H-x(1))^2+(1-x(2))^2)*(sqrt(x(2))+1)); 
-(x(1)-x(2))^2/(sqrt(x(1)^2+x(2)^2)*sqrt(x(2))*x(2))-
(2*(1-x(2))*sqrt(x(2))*(sqrt(x(2))+1)+(L/H-x(1))^2+(1-x(2))^2)
/(sqrt(x(2))*sqrt((L/H-x(1))^2+(1-x(2))^2)*(sqrt(x(2))+1)^2)];
[x,fval] = fsolve(f,[1,1.3]); 

fsolve completed because the vector of function values is near zero
as measured by the value of the function tolerance, and
the problem appears regular as measured by the gradient.

Creamos un script que realiza las siguientes tareas:

• Busca el mínimo de T empleando la función fminsearch de MATLAB, que devuelve las coordenadas (x₁, y₁) del punto de unión de los dos planos inclinados. En el código x₁ es x(1) e y₁ es x(2). El punto inicial de partida que hay que pasarle a fminsearch, se toma próximo a la cicloide que pasa por A y B.

Para ello, representamos la cicloide

L=5;
H=1;
f=@(x) (1-cos(x))/(x-sin(x))-H/L;
phi=fzero(f,pi);
R=H/(1-cos(phi));
xp=@(th) R*(th-sin(th));
yp=@(th) R*(1-cos(th));
fplot(xp,yp,[0,phi])
set (gca,'Ydir','reverse')
axis equal
grid on
xlabel('x')
ylabel('y')
title('cicloide')

Con el puntero del ratón se marca un punto próximo a la cicloide y se leen sus coordenadas X e Y



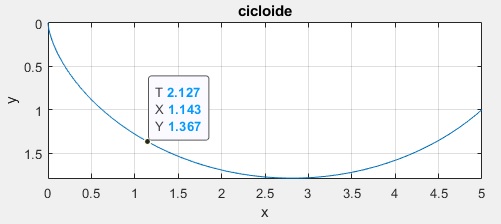
• Representa la cicloide que pasa por el origen A y por el punto B (L=5, H=1).

• Calcula el tiempo t₁ que emplea la partícula en desplazarse por el primer plano inclinado y el tiempo t₂ que emplea en recorrer el segundo

• Calcula el tiempo total t₁+t₂ que le lleva a la partícula recorrer el camino formado por los dos planos inclinados que unen los puntos A y B, y el tiempo t_c que tardaría en desplazarse por la cicloide que une ambos puntos (En la página previa, en el apartado titulado 'Tiempo que tarda la partícula en discribir un arco de cicloide', se proporciona la fórmula)

L=5;
H=1;
f=@(x) sqrt(x(1)^2+x(2)^2)/sqrt(x(2))+sqrt((L/H-x(1))^2+(1-x(2))^2)/(sqrt(x(2))+1);
x=fminsearch(f,[1.1,1.4]);
%cicloide
f=@(x) (1-cos(x))/(x-sin(x))-H/L;
phi=fzero(f,pi);
R=H/(1-cos(phi));
xp=@(th) R*(th-sin(th));
yp=@(th) R*(1-cos(th));
hold on
fplot(xp,yp,[0,phi],'color','r')
%planos inclinados
line([0,x(1)],[0,x(2)],'lineWidth',1.5,'color','b')
line([x(1),L],[x(2),H],'lineWidth',1.5,'color','b')
plot(x(1),x(2),'o','markersize',3,'markeredgecolor','r','markerfacecolor','r')
hold off
set (gca,'Ydir','reverse')
axis equal
grid on
xlabel('x')
ylabel('y')
title('cicloide')
%tiempos
t1=sqrt(x(1)^2+x(2)^2)*sqrt(2*H/9.8)/sqrt(x(2));
t2=sqrt((L/H-x(1))^2+(1-x(2))^2)*sqrt(2*H/9.8)/(sqrt(x(2))+1);
tc=phi*sqrt(R/9.8); %cicloide
format long
disp([t1+t2, tc])
format short

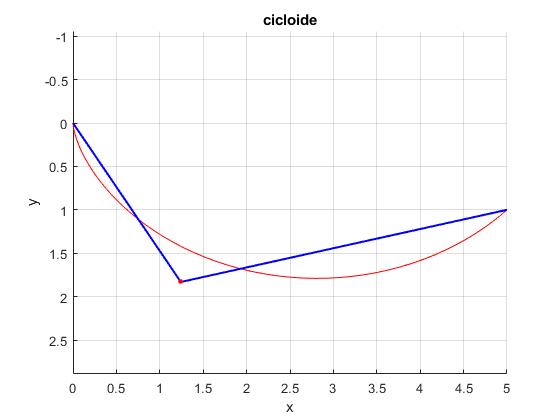
    1.477536416243312   1.388364604578311
>> t1,t2
t1 =    0.7388
t2 =    0.7388

El tiempo que tarda en recorrer el arco de cicloide es 1.388 y los dos planos inclinados 1.477. Comprobamos que los tiempos t₁ y t₂ son casi idénticos.

Tres rampas

${\displaystyle T=\frac{\sqrt{X_1^2+Y_1^2}}{\sqrt{Y_1}}+\frac{\sqrt{{\left(X_2-X_1\right)}^2+{\left(Y_2-Y_1\right)}^2}}{\sqrt{Y_1}+\sqrt{Y_2}}+\frac{\sqrt{{\left(\frac{L}{H}-X_2\right)}^2+{\left(1-Y_2\right)}^2}}{\sqrt{Y_2}+1}}$

Calculamos el mínimo del tiempo adimensional T que emplea la partícula en desplazarse a lo largo del camino formado por los tres planos inclinados que conectan el origen A y el punto B (L=5, H=1). Determinamos las coordendas de los puntos de unión (x₁, y₁) y (x₂, y₂) mediante fminsearch de MATLAB.

En el código x₁ es x(1) e y₁ es x(2), x₂ es x(3) e y₂ es x(4). Los dos puntos iniciales de partida que hay que pasarle a fminsearch, se toman próximos a la cicloide que pasa por A y B

L=5;
H=1;
f=@(x) sqrt(x(1)^2+x(2)^2)/sqrt(x(2))+sqrt((x(3)-x(1))^2+(x(4)-x(2))^2)
/(sqrt(x(2))+sqrt(x(4)))+sqrt((L/H-x(3))^2+(1-x(4))^2)/(sqrt(x(4))+1);
x=fminsearch(f,[1,1.3,3.2,1.7]);
%cicloide
f=@(x) (1-cos(x))/(x-sin(x))-H/L;
phi=fzero(f,pi);
R=H/(1-cos(phi));
xp=@(th) R*(th-sin(th));
yp=@(th) R*(1-cos(th));
hold on
fplot(xp,yp,[0,phi],'color','r')
%planos inclinados
line([0,x(1)],[0,x(2)],'lineWidth',1.5,'color','b')
line([x(1),x(3)],[x(2),x(4)],'lineWidth',1.5,'color','b')
line([x(3),L],[x(4),H],'lineWidth',1.5,'color','b')
plot(x(1),x(2),'o','markersize',3,'markeredgecolor','r','markerfacecolor','r')
plot(x(3),x(4),'o','markersize',3,'markeredgecolor','r','markerfacecolor','r')
hold off
set (gca,'Ydir','reverse')
axis equal
grid on
xlabel('x')
ylabel('y')
title('cicloide')
%tiempos
t1=sqrt(x(1)^2+x(2)^2)*sqrt(2*H/9.8)/sqrt(x(2));
t2=sqrt((x(3)-x(1))^2+(x(4)-x(2))^2)*sqrt(2*H/9.8)/(sqrt(x(2))+sqrt(x(4)));
t3=sqrt((L/H-x(3))^2+(1-x(4))^2)*sqrt(2*H/9.8)/(sqrt(x(4))+1);
tc=phi*sqrt(R/9.8); %cicloide
format long
disp([t1+t2+t3, tc])
format short

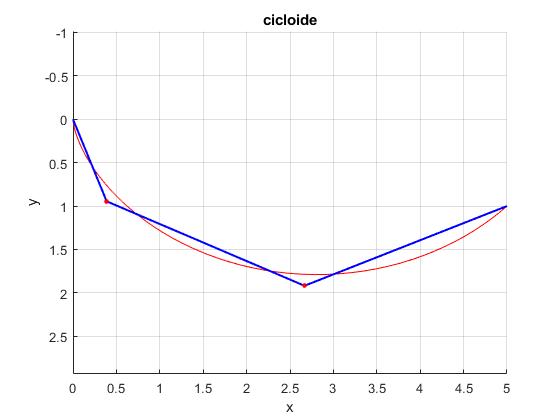
   1.424572580985510   1.388364604578311
>> t1,t2,t3
t1 =    0.4749
t2 =    0.4749
t3 =    0.4749

El tiempo que emplea la partícula en recorrer el arco de cicloide es 1.388 y el camino formado por los tres planos inclinados, 1.425 más próximo que con dos rampas. Comprobamos que los tiempos t₁, t₂ y t₃ son casi idénticos.

Cuatro rampas

${\displaystyle T=\frac{\sqrt{X_1^2+Y_1^2}}{\sqrt{Y_1}}+\frac{\sqrt{{\left(X_2-X_1\right)}^2+{\left(Y_2-Y_1\right)}^2}}{\sqrt{Y_1}+\sqrt{Y_2}}+\frac{\sqrt{{\left(X_3-X_2\right)}^2+{\left(Y_3-Y_2\right)}^2}}{\sqrt{Y_2}+\sqrt{Y_3}}+\frac{\sqrt{{\left(\frac{L}{H}-X_3\right)}^2+{\left(1-Y_3\right)}^2}}{\sqrt{Y_3}+1}}$

Calculamos el mínimo del tiempo adimensional T que emplea la partícula en desplazarse a lo largo del camino formado por cuatro planos inclinados que conectan el origen A y el punto B (L=5, H=1). Determinamos las coordendas de los puntos de unión (x₁, y₁), (x₂, y₂) y (x₃, y₃) mediante fminsearch de MATLAB..

En el código x₁ es x(1) e y₁ es x(2), x₂ es x(3) e y₂ es x(4), x₄ es x(5) e y₄ es x(6)

L=5;
H=1;
f=@(x) sqrt(x(1)^2+x(2)^2)/sqrt(x(2))+sqrt((x(3)-x(1))^2+(x(4)-x(2))^2)
/(sqrt(x(2))+sqrt(x(4)))+sqrt((x(5)-x(3))^2+(x(6)-x(4))^2)/(sqrt(x(4))+
sqrt(x(6)))+sqrt((L/H-x(5))^2+(1-x(6))^2)/(sqrt(x(6))+1);
x=fminsearch(f,[0.3,0.6,1,1.3,3.2,1.7]);
%cicloide
f=@(x) (1-cos(x))/(x-sin(x))-H/L;
phi=fzero(f,pi);
R=H/(1-cos(phi));
xp=@(th) R*(th-sin(th));
yp=@(th) R*(1-cos(th));
hold on
fplot(xp,yp,[0,phi],'color','r')
%planos inclinados
line([0,x(1)],[0,x(2)],'lineWidth',1.5,'color','b')
line([x(1),x(3)],[x(2),x(4)],'lineWidth',1.5,'color','b')
line([x(3),x(5)],[x(4),x(6)],'lineWidth',1.5,'color','b')
line([x(5),L],[x(6),H],'lineWidth',1.5,'color','b')
plot(x(1),x(2),'o','markersize',3,'markeredgecolor','r','markerfacecolor','r')
plot(x(3),x(4),'o','markersize',3,'markeredgecolor','r','markerfacecolor','r')
plot(x(5),x(6),'o','markersize',3,'markeredgecolor','r','markerfacecolor','r')
hold off
set (gca,'Ydir','reverse')
axis equal
grid on
xlabel('x')
ylabel('y')
title('cicloide')
%tiempos
t1=sqrt(x(1)^2+x(2)^2)*sqrt(2*H/9.8)/sqrt(x(2));
t2=sqrt((x(3)-x(1))^2+(x(4)-x(2))^2)*sqrt(2*H/9.8)/(sqrt(x(2))+sqrt(x(4)));
t3=sqrt((x(5)-x(3))^2+(x(6)-x(4))^2)*sqrt(2*H/9.8)/(sqrt(x(4))+sqrt(x(6)));
t4=sqrt((L/H-x(5))^2+(1-x(6))^2)*sqrt(2*H/9.8)/(sqrt(x(6))+1);
tc=phi*sqrt(R/9.8); %cicloide
format long
disp([t1+t2+t3+t4, tc])
format short

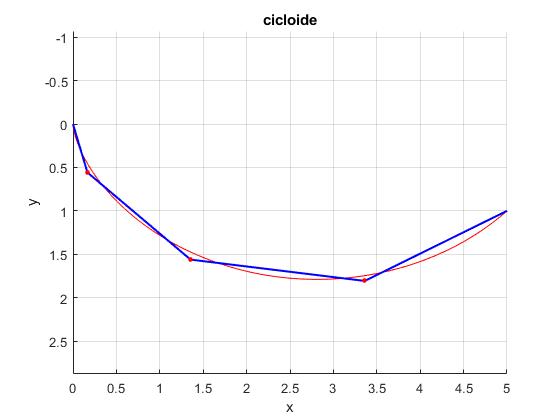
   1.408145004708376   1.388364604578311
>> t1,t2,t3,t4
t1 =    0.3520
t2 =    0.3520
t3 =    0.3520
t4 =    0.3520
x =
    0.1663    0.5577    1.3547    1.5616    3.3612    1.8073

El tiempo que emplea la partícula en recorrer el arco de cicloide es 1.388 y el camino formado por los tres planos inclinados, 1.408 más próximo que con tres rampas. Comprobamos que los tiempos t₁, t₂, t₃ y t₄ son casi idénticos. Las coordendas de los puntos de unión son (x₁, y₁)=(0.1663, 0.5577), (x₂, y₂)=(1.3547, 1.5616), (x₃, y₃)=(3.3612, 1.8073)

Propiedades de la braquistócrona discreta

Las propiedades de la braquistócrona discreta son

1. Los tiempos que la partícula emplea en recorrer los planos inclinados son iguales: t₁=t₂=...t_k=...t_N

2. Se cumple la relación



${\displaystyle \begin{array}{l}\frac{v_1}{\sin {\theta }_1}=\frac{v_2}{\sin {\theta }_2}=\mathrm{...}=\frac{v_N}{\sin {\theta }_N}=V_0\\ v_k=V_0\sin {\theta }_k,k=\mathrm{1,2...}N\end{array}}$

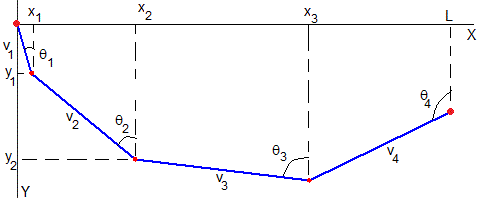
Donde θ_k es el ángulo del plano inclinado con la dirección vertical y v_k es la velocidad media de la partícula en la rampa k. Añadimos estas líneas de código al script anterior para comprobarlo

...
th_1=atan2(x(1),x(2)); %ángulos
th_2=atan2((x(3)-x(1)),(x(4)-x(2)));
th_3=atan2((x(5)-x(3)),(x(6)-x(4)));
th_4=atan2((L/H-x(5)),(1-x(6)));

k1=sqrt(x(2))/sin(th_1);
k2=(sqrt(x(2))+sqrt(x(4)))/sin(th_2);
k3=(sqrt(x(4))+sqrt(x(6)))/sin(th_3);
k4=(sqrt(x(6))+1)/sin(th_4);
disp([k1,k2,k3,k4])

    2.6135    2.6134    2.6134    2.6134

Esta relación nos recuerda a la ley de la refracción que se deduce de la aplicación del principio de Fermat: la trayectoria que sigue un rayo de luz entre dos puntos es aquella en la que emplea un tiempo mínimo en recorrerla.

Para cinco rampas el comando fminsearch de MATLAB emite un aviso

Exiting: Maximum number of function evaluations has been exceeded
         - increase MaxFunEvals option.

Con tres o cuatro rampas que unen dos puntos A y B, nos aproximamos bastante bien a la cicloide que pasa por dichos puntos

Coordenadas de los puntos de unión de los planos inclinados

Teniendo en cuenta las dos propiedades de la braquistócrona discreta, vamos a calcular las coordenadas (x_k, y_k), k=1,2,...N-1 de los puntos de unión de los N planos inclinados que conectan el origen A y el punto B(L, H)

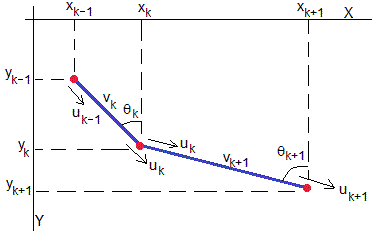
En la figura se muestran dos planos inclinados consecutivos, conectados en el punto (x_k, y_k). Relacionamos las velocidades al comienzo y al final de los dos planos inclinados

${\displaystyle \begin{array}{l}\{\begin{array}{l}{u}_k=u_{k-1}+g\cos {\theta }_k{t}_k\\ u_{k+1}=u_k+g\cos {\theta }_{k+1}{t}_{k+1}\end{array}\\ t_k=t_{k+1}=t_0\end{array}}$

En los movimientos uniformemente acelerados, las velocidades medias en cada uno de los planos inclinados son

${\displaystyle \begin{array}{l}\{\begin{array}{l}{v}_k=\frac{1}{2}\left(u_k+u_{k-1}\right)\\ v_{k+1}=\frac{1}{2}\left(u_{k+1}+u_k\right)\end{array}\\ \{\begin{array}{l}{v}_k=V_0\sin {\theta }_k\\ v_{k+1}=V_0\sin {\theta }_{k+1}\end{array}\end{array}}$

A partir de estas relaciones, despejamos la velocidad u_k

${\displaystyle \begin{array}{l}\{\begin{array}{l}{u}_k=v_k+\frac{1}{2}g\cos {\theta }_k{t}_0\\ u_k=v_{k+1}-\frac{1}{2}g\cos {\theta }_{k+1}{t}_0\end{array}\\ \sin {\theta }_{k+1}-\sin {\theta }_k=\frac{g{t}_0}{2V_0}\left(\cos {\theta }_{k+1}+\cos {\theta }_k\right)\end{array}}$

Utilizando las relaciones trigonométricas: sin(A+B)-sin(A-B)=2cosAsinB, cos(A+B)-cos(A-B)=2cosAcosB

${\displaystyle \begin{array}{l}\sin \left(\frac{1}{2}({\theta }_{k+1}-{\theta }_k)\right)=\frac{g{t}_0}{2V_0}\cos \left(\frac{1}{2}({\theta }_{k+1}-{\theta }_k)\right)\\ \tan \left(\frac{1}{2}({\theta }_{k+1}-{\theta }_k)\right)=\frac{g{t}_0}{2V_0}\end{array}}$

La diferencia entre dos ángulos consecutivos θ_k+1-θ_k es constante,

Precisamos calcular el primer ángulo, θ₁ para aplicar la relación de recurrencia. Como la partícula parte del origen A en reposo, u₀=0

${\displaystyle \begin{array}{l}\{\begin{array}{l}{u}_1=g\cos {\theta }_1{t}_0\\ v_1=\frac{u_1}{2}\end{array}\\ v_1=V_0\sin {\theta }_1\end{array}}$

De estas relaciones, obtenemos el primer ángulo

${\displaystyle \tan {\theta }_1=\frac{g{t}_0}{2V_0}}$

El resto de los ángulos se calcula fácilmente

${\displaystyle \begin{array}{l}\frac{1}{2}\left({\theta }_2-{\theta }_1\right)=\arctan \left(\frac{g{t}_0}{2V_0}\right),{\theta }_2={\theta }_1+2{\theta }_1=3{\theta }_1\\ \frac{1}{2}\left({\theta }_3-{\theta }_2\right)=\arctan \left(\frac{g{t}_0}{2V_0}\right),{\theta }_3={\theta }_2+2{\theta }_1=5{\theta }_1\\ \mathrm{...}\\ {\theta }_k=(2k-1){\theta }_1\end{array}}$

Las longitudes l_k de los planos inclinados están relacionados con el ángulo θ_k

${\displaystyle \begin{array}{l}\{\begin{array}{l}{l}_k=v_k{t}_k=V_0\sin {\theta }_k{t}_0\\ l_1=v_1{t}_1=V_0\sin {\theta }_1{t}_0\end{array}\\ l_k=l_1\frac{\sin {\theta }_k}{\sin {\theta }_1}\end{array}}$

Volviendo a la figura del apartado 'Propiedades de la braquistócrona discreta'

${\displaystyle \begin{array}{l}L={\displaystyle \sum _{k=1}^N{l}_k\sin {\theta }_k}=\frac{l_1}{\sin {\theta }_1}{\displaystyle \sum _{k=1}^N{\sin }^2\left((2k-1){\theta }_1\right)}=\frac{l_1}{\sin {\theta }_1}{S}_L({\theta }_1)\\ H={\displaystyle \sum _{k=1}^N{l}_k\cos {\theta }_k}=\frac{l_1}{\sin {\theta }_1}{\displaystyle \sum _{k=1}^N\sin \left((2k-1){\theta }_1\right)}\cos \left((2k-1){\theta }_1\right)=\frac{l_1}{\sin {\theta }_1}{S}_H({\theta }_1)\end{array}}$

Eliminando l₁ del sistema de ecuaciones, obtenemos una ecuación transcendente en θ₁

${\displaystyle \frac{L}{H}=\frac{S_L({\theta }_1)}{S_H({\theta }_1)}}$

Una vez que hemos obtenido θ₁, calculamos la longitud del primer plano inclinado, l₁ utilizando cualquiera de las dos ecuaciones

${\displaystyle l_1=L\frac{\sin {\theta }_1}{S_L({\theta }_1)}}$

Las coordenadas del punto de unión del primer y segundo plano inclinados son

${\displaystyle \{\begin{array}{l}{x}_1=l_1\sin {\theta }_1\\ y_1=l_1\cos {\theta }_1\end{array}}$

y a continuación, las coordenadas del los otros puntos de unión empleando las relaciones de recurrencia entre longitudes l_k y ángulos θ_k

${\displaystyle \begin{array}{l}{\theta }_k=(2k-1){\theta }_1\\ l_k=l_1\frac{\sin {\theta }_k}{\sin {\theta }_1}\\ \{\begin{array}{l}{x}_k=x_{k-1}+l_k\sin {\theta }_k\\ y_k=y_{k-1}+l_k\cos {\theta }_k,k=\mathrm{2,3,...}N-1\end{array}\end{array}}$

Para calcular θ₁, definimos la función que pasamos a fzero de MATLAB

function res =cicloide_discreta(th, N)
    num=0;
    den=0;
    for k=1:N
        num=num+sin((2*k-1)*th).^2;
        den=den+sin((2*k-1)*th).*cos((2*k-1)*th);
    end
    res=num./den;
end

Calculamos las coordenadas de los puntos de unión de N=4 planos inclinados. Representamos el camino mediante segmentos de color azul

Representamos la cicloide que pasa por el origen A y por el punto B (L=5, H=1)

L=5;
H=1;
N=4; %número de rampas
x=zeros(N-1,1);
y=zeros(N-1,1);
f=@(th) cicloide_discreta(th,N)-L/H;
th_1=fzero(f,0.1);
k=1:N;
SL=sum(sin((2*k-1)*th_1).^2);
l1=L*sin(th_1)/SL;
x(1)=l1*sin(th_1);
y(1)=l1*cos(th_1);
for k=2:N-1
    x(k)=x(k-1)+l1*sin((2*k-1)*th_1)^2/sin(th_1);
    y(k)=y(k-1)+l1*sin((2*k-1)*th_1)*cos((2*k-1)*th_1)/sin(th_1);
end
td=N*sqrt(2*L*tan(th_1)/(SL*9.8)); %tiempo, planos inclinados
%cicloide
f=@(x) (1-cos(x))/(x-sin(x))-H/L;
phi=fzero(f,pi);
R=H/(1-cos(phi));
xp=@(th) R*(th-sin(th));
yp=@(th) R*(1-cos(th));
hold on
fplot(xp,yp,[0,phi],'color','r')
%planos inclinados
line([0,x(1)],[0,y(1)],'lineWidth',1.5,'color','b')
for k=2:N-1
    line([x(k-1),x(k)],[y(k-1),y(k)],'lineWidth',1.5,'color','b')
end
line([x(3),L],[y(3),H],'lineWidth',1.5,'color','b')
for k=1:N-1
    plot(x(k),y(k),'o','markersize',3,'markeredgecolor','r','markerfacecolor','r')
end
tc=phi*sqrt(R/9.8); %tiempo cicloide
disp([td,tc]);
hold off
set (gca,'Ydir','reverse')
axis equal
grid on
xlabel('x')
ylabel('y')
title('cicloide')

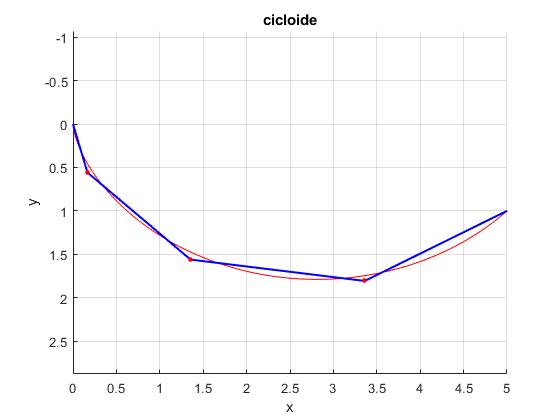
Obtenemos la misma figura y las mismas coordenadas de los puntos de unión de los planos inclinados que hemos obtenido utilizando fminsearch: (x₁, y₁)=(0.1663, 0.5577), (x₂, y₂)=(1.3547, 1.5616), (x₃, y₃)=(3.3612, 1.8073)

x =
    0.1663
    1.3547
    3.3612
>> y
y =
    0.5577
    1.5616
    1.8073

El problema principal reside en estimar el intervalo (en el que la función cicloide_discreta cambia de signo) que tenemos que pasar a fzero para calcular el ángulo θ₁. Por ejemplo, para N=4, el denominador es la suma, sin(2θ)+sin(6θ)+sin(10θ)+sin(14θ), que se hace cero para θ≈0.4 rad. La representación gráfica de dicha función con el comando fplot nos puede ayudar

Tiempo

t₀ es el tiempo que emplea la partícula en deslizar sin rozamiento a lo largo de un plano inclinado y es constante. El tiempo total que le lleva desplazarse de A a B a lo largo del camino formado por un conjunto de N planos inclinados es, t_d=Nt₀. Utilizamos las siguientes relaciones para calcular t₀

${\displaystyle \begin{array}{l}{l}_1=L\frac{\sin {\theta }_1}{S_L({\theta }_1)}\\ l_1=V_0{t}_0\sin {\theta }_1\\ \tan {\theta }_1=\frac{g{t}_0}{2V_0}\\ t_0=\sqrt{2\frac{L\tan {\theta }_1}{S_L({\theta }_1)·g}}\end{array}}$

El tiempo t_d=1.0481 coincide con el calculado empleando fminsearch de MATLAB

    1.4081    1.3884

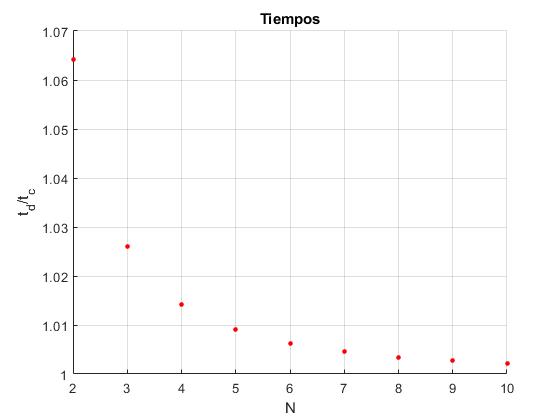
Representamos el cociente de tiempos t_d/t_c para N=2,3...10, planos inclinados que conectan el origen A y el punto B (L=5, H=1). Comprobamos que cuando N se hace grande, el cociente t_d/t_c→1

L=5;
H=1;
hold on
for N=2:10
    %planos inclinados
    f=@(th) cicloide_discreta(th,N)-L/H;
    th_1=fzero(f,0.1);
    k=1:N;
    SL=sum(sin((2*k-1)*th_1).^2);
    td=N*sqrt(2*L*tan(th_1)/(SL*9.8)); %tiempo, planos inclinados
%cicloide
    f=@(x) (1-cos(x))/(x-sin(x))-H/L;
    phi=fzero(f,pi);
    R=H/(1-cos(phi));
    tc=phi*sqrt(R/9.8); %tiempo cicloide
    plot(N,td/tc,'o','markersize',3,'markeredgecolor','r','markerfacecolor','r')
end
hold off
grid on
xlabel('N')
ylabel('t_d/t_c')
title('Tiempos')

Referencias

David Agmon, Hezi Yizhaq. The remarkable properties of the discrete brachistochrone. Eur. J. Phys. 40(2019) 035005

Carl E Mungan, Trevor C Lipscombe. Minimum descent time along a set of connected inclined planes. Eur. J. Phys. 38(2017) 045002