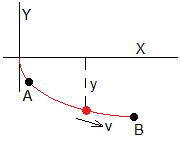
Se trata de encontrar la curva que hace que una partícula que cae bajo la acción de la gravedad, emplee un tiempo mínimo en recorrerla. Utilizaremos el cálculo de variaciones para obtener la ecuación de la curva que como veremos es una cicloide

La partícula parte del origen con velocidad v=0. Cuando ha descendido una altura y, su velocidad es v, que se calcula aplicando el principio de conservación de la energía

${\displaystyle \begin{array}{l}\frac{1}{2}m{v}^2+mg(-y)=0\\ v=\sqrt{2gy}\end{array}}$

El tiempo que tarda la partícula en ir de A a B es

${\displaystyle I(y)={\displaystyle \underset{A}{\overset{B}{\int }}dt}={\displaystyle \underset{A}{\overset{B}{\int }}\frac{ds}{v}}=\frac{1}{\sqrt{2g}}{\displaystyle \underset{A}{\overset{B}{\int }}\frac{\sqrt{1+{\dot{y}}^2}dx}{\sqrt{y}}}}$

Aplicando la ecuación de Euler-Lagrange a la función f que no depende de x

${\displaystyle f(x,y,\dot{y})=\frac{\sqrt{1+{\dot{y}}^2}}{\sqrt{y}}}$

por lo que utilizamos la segunda versión de dicha ecuación

${\displaystyle \begin{array}{l}\frac{\partial f}{\partial \dot{y}}=\frac{\dot{y}}{\sqrt{y}\sqrt{1+{\dot{y}}^2}}\\ \frac{d}{dx}\left(\dot{y}\frac{\partial f}{\partial \dot{y}}-f\right)=0\\ \frac{{\dot{y}}^2}{\sqrt{y}\sqrt{1+{\dot{y}}^2}}-\frac{\sqrt{1+{\dot{y}}^2}}{\sqrt{y}}=C\end{array}}$

El resultado es

${\displaystyle \begin{array}{l}-\frac{1}{\sqrt{y}\sqrt{1+{\dot{y}}^2}}=C\\ \frac{dy}{dx}=\sqrt{\frac{k-y}{y}}\\ {\displaystyle \int \sqrt{\frac{y}{k-y}}dy+C_1=x}\end{array}}$

Hacemos el cambio de variable

${\displaystyle \begin{array}{l}y=k{\sin }^2\theta \\ dy=2k\sin \theta \cos \theta ·d\theta \\ {\displaystyle \int \sqrt{\frac{y}{k-y}}dy}=2k{\displaystyle \int \tan \theta }\sin \theta \cos \theta ·d\theta =2k{\displaystyle \int {\sin }^2\theta ·d\theta =k}{\displaystyle \int \left(1-\cos (2\theta )\right)d\theta }=\\ k\left(\theta -\frac{1}{2}\sin (2\theta )\right)\\ x=k\left(\theta -\frac{1}{2}\sin (2\theta )\right)+C_1\end{array}}$

La constante C₁ se determina sabiendo que la trayectoria pasa por el origen (x=0, y=0). Teniendo en cuenta que y=0, entonces $k{\sin }^2\theta =0$, tendremos que θ=0, lo que implica que C₁=0

${\displaystyle \begin{array}{l}x=k\left(\theta -\frac{1}{2}\sin \left(2\theta \right)\right)\hfill \\ y=k{\sin }^2\theta =\frac{k}{2}\left(1-\cos \left(2\theta \right)\right)\hfill \end{array}}$

Llamando R=k/2 y φ=2θ

${\displaystyle \begin{array}{l}x=R\left(\phi -\sin \phi \right)\\ y=R\left(1-\cos \phi \right)\end{array}}$

Que son las ecuaciones paramétricas de la curva denominada cicloide

Vamos a determinar el valor del parámetro R para que la cicloide pase por el punto (x₁, y₁). Para ello, hay que calcular la raíz φ₁ de la ecuación trascendente

${\displaystyle \frac{y_1}{x_1}=\frac{1-\cos \phi }{\phi -\sin \phi }}$

Conocidos y₁ y φ₁ calculamos R,

${\displaystyle R=\frac{y_1}{1-\cos {\phi }_1}}$

Representamos las cicloides que parten del origen y pasan por los puntos (2, 2·2/π), (2, 0.5) y (2,2). Corresponden a tres casos distintos: y₁=2x₁/π (en color azul), y₁<2x₁/π, y₁>2x₁/π

x1=[2,2,2];
y1=[2*2/pi,0.5,2];
hold on
for i=1:length(x1)
    f=@(x) (1-cos(x))/(x-sin(x))-y1(i)/x1(i);
    phi=fzero(f,pi);
    R=y1(i)/(1-cos(phi));
    xp=@(th) R*(th-sin(th));
    yp=@(th) R*(1-cos(th));
    fplot(xp,yp,[0,2*pi])
    plot(x1(i),y1(i),'o','markersize',3,'markeredgecolor','r',
'markerfacecolor','r')
end
set (gca,'Ydir','reverse')
axis equal
legend('y_1=2*x_1/\pi','', 'y_1<2*x_1/\pi','', 'y_1>2*x_1/\pi',
'location', 'best')
grid on
xlim([0,4])
xlabel('x')
ylabel('y')
title('Cicloides')

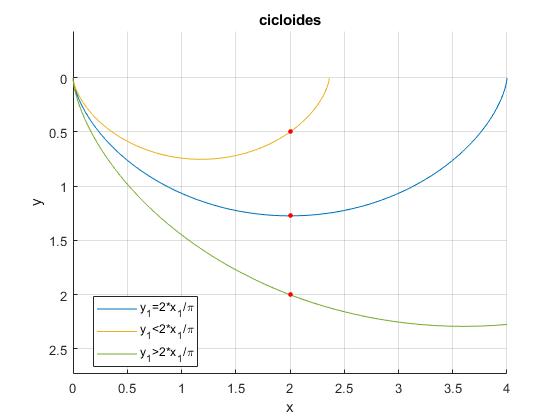
En el segundo caso (primera trayectoria en la figura), la partícula desciende por debajo de y₁ y luego, vuelve a ascender hasta alcanzar la posición final (x₁, y₁) y aún así, emplea un tiempo mínimo

Tiempo que tarda la partícula en discribir un arco de cicloide

Conocida la trayectoria que sigue la partícula, calculamos el tiempo T que tarda en moverse entre dos puntos A y B de una trayectoria y(x)

${\displaystyle T={\displaystyle \underset{A}{\overset{B}{\int }}\frac{ds}{v}}=\frac{1}{\sqrt{2g}}{\displaystyle \underset{A}{\overset{B}{\int }}\frac{\sqrt{1+{\dot{y}}^2}dx}{\sqrt{y}}}}$

Para una cicloide, expresamos y, dy/dx y dx en términos de los parámetros R y φ

${\displaystyle \begin{array}{l}\frac{dx}{d\phi }=R\left(1-\cos \phi \right)\frac{dy}{d\phi }=R\sin \phi \\ \frac{dy}{dx}=\frac{\sin \phi }{1-\cos \phi }{\left(\frac{dy}{dx}\right)}^2=\frac{1+\cos \phi }{1-\cos \phi }\\ T=\frac{1}{\sqrt{2g}}{\displaystyle \underset{A}{\overset{B}{\int }}\frac{\sqrt{1+\frac{1+\cos \phi }{1-\cos \phi }}}{\sqrt{R\left(1-\cos \phi \right)}}}R\left(1-\cos \phi \right)d\phi =\sqrt{\frac{R}{g}}{\displaystyle \underset{{\phi }_A}{\overset{{\phi }_B}{\int }}d\phi }\end{array}}$

Si A es el origen φ=0 y si B es el punto (x₁, y₁), calculamos la raíz φ₁ de la ecuación trascendente y después, el parámetro R, tal como hemos hecho anteriormente

El tiempo T que tarda en llegar la partícula al punto B describiendo un arco de cicloide, partiendo del origen en reposo es

${\displaystyle T=\sqrt{\frac{R}{g}}{\phi }_1}$

x1=2; %punto B
y1=2;
f=@(x) (1-cos(x))/(x-sin(x))-y1/x1;
phi=fzero(f,pi);
R=y1/(1-cos(phi));
T=sqrt(R/10)*phi; %tiempo
disp(T);

    0.8165

Comparación con otras trayectorias

Vamos a calcular el tiempo que tarda una partícula en desplazarse desde el origen A hasta el punto B(x₁,y₁), siguiendo varias trayectorias, comprobando que la cicloide es la que tarda el menor tiempo.

Línea recta

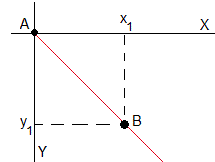
Consideremos la línea recta que une el origen A y el punto B(x₁,y₁).

${\displaystyle \begin{array}{l}y=\frac{y_1}{x_1}x\\ dy=\frac{y_1}{x_1}dx\end{array}}$

El tiempo que tarda en moverse de A a B partiendo del reposo es

${\displaystyle \begin{array}{l}T=\frac{1}{\sqrt{2g}}{\displaystyle \underset{A}{\overset{B}{\int }}\frac{1}{\sqrt{y}}}\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}dx\\ T=\frac{1}{\sqrt{2g}}\sqrt{\frac{x_1^2+y_1^2}{x_1{y}_1}}{\displaystyle \underset{0}{\overset{x1}{\int }}\frac{1}{\sqrt{x}}dx=}\sqrt{\frac{2}{g}}\sqrt{\frac{x_1^2+y_1^2}{x_1{y}_1}}\sqrt{x_1}\end{array}}$

x1=2; %punto P
y1=2;
T=sqrt(2/9.8)*sqrt((x1^2+y1^2)/(x1*y1))*sqrt(x1);
disp(T);

    0.9035

Parábola

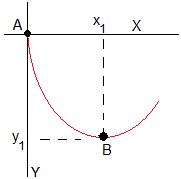
Consideremos la parábola que pasa por el origen A y el punto B(x₁,y₁).

La ecuación de la parábola que pasa por el origen es y=ax²+bx, y tiene su vértice en el punto B(x₁,y₁) es

${\displaystyle \begin{array}{l}y=a{x}^2+bx\\ \frac{dy}{dx}=2ax+b\end{array}}$

Resolvemos el sistema de dos ecuaciones

${\displaystyle \begin{array}{l}2a{x}_1+b=0\\ y_1=a{x}_1^2+b{x}_1\end{array}\}a=-\frac{y_1}{x_1^2}b=2\frac{y_1}{x_1}}$

El tiempo que tarda en moverse de A a B partiendo del reposo es

${\displaystyle T=\frac{1}{\sqrt{2g}}{\displaystyle \underset{0}{\overset{x_1}{\int }}\sqrt{\frac{1+{\left(2ax+b\right)}^2}{a{x}^2+bx}}}dx}$

Utilizamos procedimientos numéricos para calcular la integral definida

x1=2; %punto P
y1=2;
a=-y1/x1^2;
b=2*y1/x1;
f=@(x) sqrt((1+(2*a*x+b).^2)./(a*x.^2+b*x));
T=integral(f,0,x1)/sqrt(2*9.8);
disp(T);

     0.8418

Función armónica

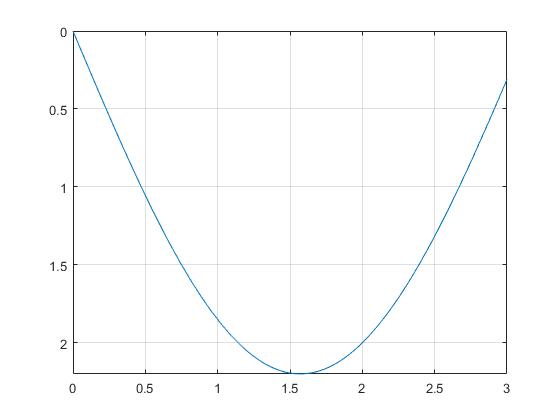
Consideremos la función armónica y=asin(x) que pasa por el origen A y el punto B(x₁,y₁).

${\displaystyle a=\frac{y_1}{\sin \left(x_1\right)}}$

Sabiendo y=y(x) y dy/dx

${\displaystyle \frac{dy}{dx}=a\cos (x)}$

calculamos el tiempo T de viaje. Resolvemos la integral definida por procedimientos numéricos

${\displaystyle T=\frac{1}{\sqrt{2g}}{\displaystyle \underset{0}{\overset{x_1}{\int }}\sqrt{\frac{1+a^2{\cos }^{2}x}{a\sin x}}dx}}$

x1=2; %punto P
y1=2;
a=-y1/x1^2;
b=2*y1/x1;
f=@(x) sqrt((1+(2*a*x+b).^2)./(a*x.^2+b*x));
T=integral(f,0,x1)/sqrt(2*9.8);
disp(T);

     0.8733
>> fplot(@(x) a*sin(x),[0,3])
>> grid on
>> set (gca,'Ydir','reverse')

Como vemos en el gráfico, la partícula parte del origen en reposo, se mueve a lo largo de la trayectoria hasta alcanzar el mínimo en π/2 y luego, asciende hasta el punto B (2,2)

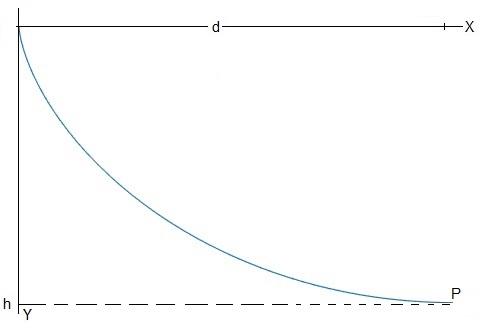
Dos segmentos

Las ecuaciones paramétricas de la braquistócrona son

${\displaystyle \begin{array}{l}x=R\left(\phi -\sin \phi \right)\\ y=R\left(1-\cos \phi \right)\end{array}}$

Cuando φ=π, y=h, por lo que R=h/2.

El punto P esta a una distancia, d=πh/2

h=1;
R=h/2;
fplot(@(th) R*(th-sin(th)),@(th) R*(1-cos(th)),[0,pi])
set (gca,'Ydir','reverse')
axis equal
grid on
axis off

El tiempo T que tarda una partícula en recorrer la trayectoria desde el origen hasta P es

${\displaystyle T=\sqrt{\frac{R}{g}}{\phi }_1=\pi \sqrt{\frac{h}{2g}}}$

Consideremos ahora la trayectoria formada por dos segmentos conectados

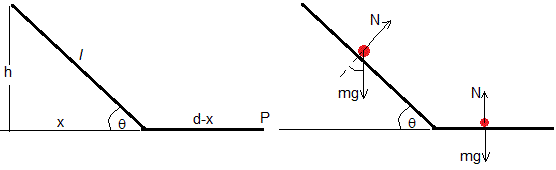
En el plano inclinado, la fuerza sobre la partícula es mgsinθ, la aceleración es gsinθ. En el plano horizontal, la fuerza sobre la partícula es nula, la velocidad es constante

Supondremos que la partícula parte en reposo. La ecuación de su movimiento a lo largo del plano inclinado es

${\displaystyle s=\frac{1}{2}g\sin \theta ·t^2,\sin \theta =\frac{h}{l}}$

El tiempo que tarda en recorrerlo es

${\displaystyle \begin{array}{l}l=\frac{1}{2}g\sin \theta ·t_1^2,l=\sqrt{x^2+h^2}\\ t_1=\sqrt{\frac{2\left(x^2+h^2\right)}{gh}}\end{array}}$

La velocidad al llegar al final del plano inclinado (principio del plano horizaontal) es

${\displaystyle v=g\sin \theta ·t_1=g\sin \theta \sqrt{\frac{2l}{g\sin \theta }}=\sqrt{2lg\sin \theta }=\sqrt{2gh}}$

La velocidad se puede obtener a partir de la conservación de la energía, mgh=mv²/2

Esta velocidad se mantiene constante en el plano horizontal

${\displaystyle \begin{array}{l}d-x=v{t}_2\\ t_2=\frac{d-x}{\sqrt{2gh}}\end{array}}$

El tiempo total es

${\displaystyle t=t_1+t_2=\sqrt{\frac{2\left(x^2+h^2\right)}{gh}}+\frac{d-x}{\sqrt{2gh}}}$

Representamos el tiempo t en función de x para tres valores de d=πh/2, 2, 3. Identificamos los mínimos de la función t(x)

h=1;
hold on
xm=h/sqrt(3); %mínimo
line([xm,xm],[0,2],'lineStyle','--')
for d=[pi*h/2, 2,3]
    f=@(x) sqrt(2*(x.^2+h^2)/(9.8*h))+(d-x)/sqrt(2*9.8*h);
    fplot(f, [0,3])
    tm=(sqrt(8/3)-sqrt(1/6))*sqrt(h/9.8)+d/sqrt(2*9.8*h); %mínimo
    line([0,xm],[tm,tm],'lineStyle','--')
end
hold off
grid on
ylim([0,1.5])
xlabel('x (m)')
ylabel('t(s)')
title('Tiempo de en función de x')

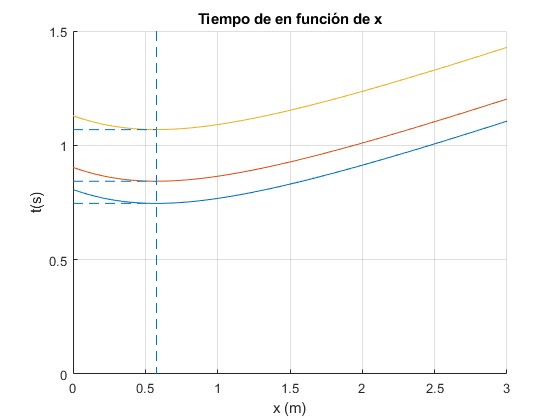
Calculamos el valor de x para que el tiempo t sea mínimo

${\displaystyle \begin{array}{l}\frac{dt}{dx}=\sqrt{\frac{2}{gh}}\frac{x}{\sqrt{x^2+h^2}}-\frac{1}{\sqrt{2gh}}=0\\ 2x=\sqrt{x^2+h^2}\\ 4x^2=x^2+h^2\\ x_m=\frac{h}{\sqrt{3}}\end{array}}$

Para este valor de x_m el tiempo mínimo vale

${\displaystyle t_m=\sqrt{\frac{2\left({\frac{h}{3}}^2+h^2\right)}{gh}}+\frac{d-\frac{h}{\sqrt{3}}}{\sqrt{2gh}}=\left(\sqrt{\frac{8}{3}}-\sqrt{\frac{1}{6}}\right)\sqrt{\frac{h}{g}}+\frac{d}{\sqrt{2gh}}}$

Comparamos el tiempo t_m con el tiempo T para la distancia d=πh/2

${\displaystyle \frac{T}{t_m}=\frac{\pi \sqrt{\frac{h}{2g}}}{\left(\sqrt{\frac{8}{3}}-\sqrt{\frac{1}{6}}\right)\sqrt{\frac{h}{g}}+\frac{\pi \frac{h}{2}}{\sqrt{2gh}}}=\frac{\frac{\pi }{\sqrt{2}}}{\sqrt{\frac{8}{3}}-\sqrt{\frac{1}{6}}+\frac{\pi }{2\sqrt{2}}}=0.9512}$

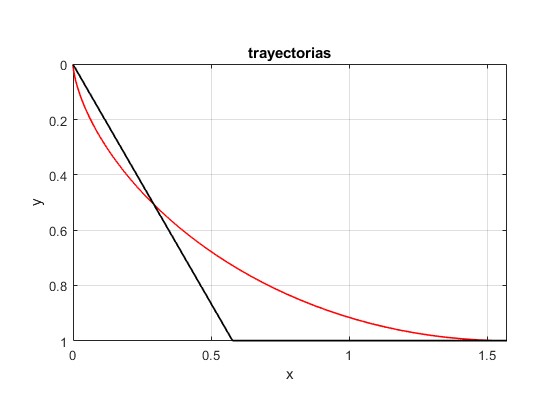
Como cabe esperar, T es más pequeño. Comparamos las dos trayectorias

h=1;
R=h/2;
fplot(@(th) R*(th-sin(th)),@(th) R*(1-cos(th)),[0,pi],'lineWidth',1.3,'color','r')
set (gca,'Ydir','reverse')
line([0,xm],[0,h],'lineWidth',1.3,'color','k')
line([xm,pi*h/2],[h,h],'lineWidth',1.3,'color','k')
axis equal
grid on
xlabel('x')
ylabel('y')
title('trayectorias')

En la página titulada Braquistócrona discreta sustituimos esta trayectoria por un conjunto de segmentos conectados

La partícula parte del origen con velocidad no nula

En este apartado analizamos cómo cambia la trayectoria cicloidal de la partícula cuando parte del origen con velocidad inicial no nula

La partícula parte del origen con velocidad v₀. Cuando ha descendido una altura y, su velocidad es v, que se calcula aplicando el principio de conservación de la energía

${\displaystyle \begin{array}{l}\frac{1}{2}m{v}^2+mg(-y)=\frac{1}{2}m{v}_0^2\hfill \\ v=\sqrt{v_0^2+2gy}\hfill \end{array}}$

El tiempo que tarda la partícula en ir de A a B es

${\displaystyle I(y)=\underset{A}{\overset{B}{{\displaystyle \int }}}dt=\underset{A}{\overset{B}{{\displaystyle \int }}}\frac{ds}{v}=\underset{A}{\overset{B}{{\displaystyle \int }}}\frac{\sqrt{1+{\dot{y}}^2}dx}{\sqrt{v_0^2+2gy}}}$

Haciendo el cambio de variable

${\displaystyle \{\begin{array}{l}x=X-K\\ y=Y-\frac{v_0^2}{2g}\end{array}}$

La integral se convierte en

${\displaystyle I(Y)=\frac{1}{\sqrt{2g}}\underset{A}{\overset{B}{{\displaystyle \int }}}\frac{\sqrt{1+{\dot{Y}}^2}dx}{\sqrt{Y}}}$

Aplicando la ecuación de Euler-Lagrange a la función f que no depende de X

${\displaystyle f(X,Y,\dot{Y})=\frac{\sqrt{1+{\dot{Y}}^2}}{\sqrt{Y}}}$

La solución ya deducida en el primer apartado, cuando la partícula partía con velocidad inicial nula, es

${\displaystyle \{\begin{array}{l}X=R(\phi -\sin \phi )\\ Y=R(1-\cos \phi )\end{array}}$

Voviendo a las variables originales x e y

${\displaystyle \{\begin{array}{l}x=R(\phi -\sin \phi )-K\\ y=R(1-\cos \phi )-\frac{v_0^2}{2g}\end{array}}$

Las constantes R y K se determina sabiendo que la curva pasa por los puntos A (0, 0) y B(x_B, y_B) o bien, resolviendo el sistema de cuatro ecuaciones

${\displaystyle \begin{array}{l}A\{\begin{array}{l}R({\phi }_A-\sin {\phi }_A)-K=0\\ R(1-\cos {\phi }_A)-\frac{v_0^2}{2g}=0\end{array}\\ B\{\begin{array}{l}R({\phi }_B-\sin {\phi }_B)-K=x_B\\ R(1-\cos {\phi }_B)-\frac{v_0^2}{2g}=y_B\end{array}\end{array}}$

Llamando $V_0=\frac{v_0^2}{2g}$, el sistema de ecuaciones se expresa de forma más conveniente

${\displaystyle \begin{array}{l}R=\frac{y_B+V_0}{1-\cos {\phi }_B}K=\left(y_B+V_0\right)\frac{{\phi }_A-\sin {\phi }_A}{1-\cos {\phi }_B}\\ \{\begin{array}{l}\left(y_B+V_0\right)\left(1-\cos {\phi }_A\right)-V_0\left(1-\cos {\phi }_B\right)=0\\ \left(y_B+V_0\right)\left({\phi }_B-\sin {\phi }_B-{\phi }_A+\sin {\phi }_A\right)-x_B\left(1-\cos {\phi }_B\right)=0\end{array}\end{array}}$

Como podemos apreciar, cuando la velocidad inicial es nula, v₀=0, φ_A=0, K=0, y φ_B se obtiene resolviendo la ecuación transcendente

${\displaystyle y_B\left({\phi }_B-\sin {\phi }_B\right)-x_B\left(1-\cos {\phi }_B\right)=0}$

Llamando x₁ a φ_A y x₂ a φ_B, tenemos que resolver el sistema de dos ecuaciones no lineales con dos incógnitas

${\displaystyle \{\begin{array}{l}{f}_1(x_1,x_2)=0\\ f_2(x_1,x_2)=0\end{array}}$

Utilizamos el procedimiento iterativo, para lo cual definimos el vector F de funciones

${\displaystyle F=\left(\begin{array}{c}\left(y_B+V_0\right)\left(1-\cos {\phi }_A\right)-V_0\left(1-\cos {\phi }_B\right)\\ \left(y_B+V_0\right)\left({\phi }_B-\sin {\phi }_B-{\phi }_A+\sin {\phi }_A\right)-x_B\left(1-\cos {\phi }_B\right)\end{array}\right)}$

El vector X de las incógnitas

${\displaystyle X=\left(\begin{array}{c}{\phi }_A\\ {\phi }_B\end{array}\right)}$

El Jacobiano de este sistema de dos ecuaciones es

${\displaystyle \begin{array}{l}J=\left(\begin{array}{cc}\frac{\partial f_1}{\partial x_1}& \frac{\partial f_1}{\partial x_2}\\ \frac{\partial f_2}{\partial x_1}& \frac{\partial f_2}{\partial x_2}\end{array}\right)\\ J=\left(\begin{array}{cc}\left(y_B+V_0\right)\sin {\phi }_A& -V_0\sin {\phi }_B\\ \left(y_B+V_0\right)\left(\cos {\phi }_A-1\right)& \left(y_B+V_0\right)\left(1-\cos {\phi }_B\right)-x_B\sin {\phi }_B\end{array}\right)\end{array}}$

Se parte de un valor inicial de las incógnitas X₀ y se obtiene la solución aproximada empeando el proceso iterativo, X=X-J\F

El proceso se detiene después de un número determinado de iteraciones o cuando la diferencia entre dos valores consecutivos del vector de las incógnitas X es menor que un número prefijado

Primero, comprobamos que cuando la velocidad inicial es nula, obtenemos las mismas trayectorias que en el primer apartado, tomando el punto B de coordenadas, por ejemplo, (2,2), después asignamos un valor a la velocidad inicial o al parámetro V₀

xB=2; %coordenadas del punto B
yB=2;
V0=2;

F=@(x) [(yB+V0)*(1-cos(x(1)))-V0*(1-cos(x(2)));(yB+V0)*(x(2)-sin(x(2))-
x(1)+sin(x(1)))-xB*(1-cos(x(2)))];
J=@(x) [(yB+V0)*sin(x(1)),-V0*sin(x(2)); (yB+V0)*(cos(x(1))-1), 
(yB+V0)*(1-cos(x(2)))-xB*sin(x(2))];
x=[pi/4;pi]; %valor inicial
i=0;
while i<100
    y=-J(x)\F(x);
    if sqrt(norm(y)/norm(x))<0.001
         break;
    end
    x=x+y;
    i=i+1;
end
if i>=100
    disp('Se ha soprepasado el número de iteracciones');
end
fprintf('La solución es phi_A=%1.3f, phi_B=%1.3f\n',x(1),x(2));

%trayectoria
R=(yB+V0)/(1-cos(x(2)));
K=R*(x(1)-sin(x(1)));
xp=@(th) R*(th-sin(th))-K;
yp=@(th) R*(1-cos(th))-V0;
hold on
fplot(xp,yp,[x(1),2*pi])
plot(xB,yB,'o','markersize',3,'markeredgecolor','r','markerfacecolor','r')
alfa=atan(sin(x(1))/(1-cos(x(1))));
quiver(0,0,sqrt(2*9.8*V0)*cos(alfa),sqrt(2*9.8*V0)*sin(alfa),'color','r') 
hold off
set (gca,'Ydir','reverse')
axis equal
grid on
xlabel('x')
ylabel('y')
title('Cicloide')

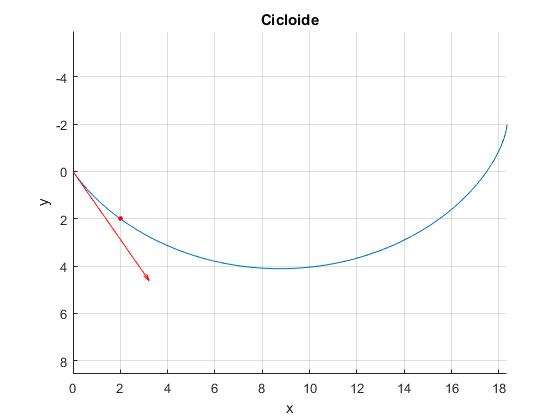
La solución es phi_A=1.218, phi_B=1.885

Cuando el móvil parte de origen con velocidad inicial $V_0=\frac{v_0^2}{2g}=2$, el parámetro φ_A=1.218, cuando llega al punto B (2,2) el parámetro φ_B=1.885

Se ha dibujado el vector velocidad inicial tangente a la trayectoria en el origen. El ángulo α que forma el vector velocidad con el eje X es

${\displaystyle \tan \alpha =\frac{dy}{dx}=\frac{dy/d\phi }{dx/d\phi }=\frac{\sin {\phi }_A}{1-\cos {\phi }_A}}$

Tiempo que tarda la partícula en discribir un arco de cicliode

El tiempo que trada la partícula en desplazarse desde el origen A al punto B es

${\displaystyle T=\sqrt{\frac{R}{g}}\left({\phi }_B-{\phi }_A\right)}$

>> T=sqrt(R/9.8)*(x(2)-x(1))
T =    0.3725

Que como vemos es bastante menor que el tiempo obtenido cuando la velocidad inicial es nula, 0.8165

Referencias

Del apartado titulado 'La partícula parte del origen con velocidad no nula'

T. M. Atanackovic. The brachistochrone for a material point with arbitrary initial velocity. Am. J. Phys. 46(12) December 1978, pp. 1274-1275

Pirooz Mohazzabi. A Different Brachistochrone Problem with Counterintuitive Results. Journal of Applied Mathematics and Physics, 2024, 12, 1426-1431, https://doi.org/10.4236/jamp.2024.124087